微纳卫星与非合作翻滚目标对接的模型预测控制

赵 玲，陈丹鹤，廖文和，郑 侃，刘婷婷

(南京理工大学机械工程学院，南京 210094)

0 引 言

航天器交会对接操作是空间在轨服务的关键技术之一,可以利用交会对接操作执行大量的空间任务,例如失效航天器在轨维修救援[1]、在轨加注[2]、空间碎片主动清理[3]等。近几年,人们提出利用微纳卫星进行空间碎片清理及卫星延寿等空间任务。通常利用一颗母星携带并运送多颗微纳子星至目标附近释放,被释放的子星与目标进行自主交会对接和同步机动以完成相应的任务。其优点在于能够在一次任务过程中,实现对多个目标开展多项在轨任务[4]。此外,相比于传统的大卫星,微纳卫星具有价格低廉、生产周期短等显著优势。

针对微纳卫星与非合作翻滚目标的对接是实现上述任务的基础,需要控制追踪星接近目标并最终停靠在相应的对接位置。同时要求追踪星与目标的对接端口的相对速度为零,相对位置恒定,姿态保持同步。首先,由于目标为失效卫星或空间碎片等可能存在翻滚的非合作目标,其普遍具有的非线性特性大大增加了接近过程的难度。其次,在交会对接的最后阶段,为了保证对接的安全性和准确性,必须严格考虑实际存在的工程约,包括控制输入饱和约,追踪星光学设备视场约,以及为了避免与目标产生碰撞,需要设定安全接近走廊约和接近过程的速度阈值等,在此多约情况下的控制是一个较为复杂的问题。最后,相比与大卫星对接,微纳卫星的对接机构尺寸更小,对误差的容忍范围更小,同时微纳卫星性能较弱,推进系统推力幅值仅为毫牛级别,需要在微纳卫星小尺寸及低性能框架下满足对接精度的要求。因此,微纳卫星与非合作翻滚目标的对接是一项具有挑战性的任务。

针对大型航天器的对接问题,学者进行了大量的研究。首先,针对对接同步控制中动力学建模问题,通常使用C-W方程进行圆轨道相对运动描述[5],在此基础上,T-H方程将适用范围拓展到椭圆轨道[6]。航天器的相对姿态通常使用姿态四元数[7]或方向余弦[8]等来描述。但实际上,追踪航天器与目标间的相对位置和姿态运动是高度非线性和耦合的,文献[9]利用对偶四元数同时描述航天器姿态和轨道动力学,解决了挠性航天器的一体化控制问题。文献[10]基于T-H方程以及误差四元数建立了相对位置和姿态的综合模型,设计了追踪航天器的标称轨迹,采用鲁棒自适应控制器完成了对目标的追踪。在动力学模型建立的基础上,需要考虑进行安全的抵近对接路径规划与控制器设计。文献[11]采用了自适应高斯伪谱方法来生成最佳轨迹,以确保超近距离飞行任务的安全。文献[12]研究了平面对接机动的抵近制导问题,提出了基于庞德里亚金最小值原理的最优能量制导方案。文献[13]利用人工势函数设计了安全约下的有限时间滑模控制器进行自主对接,有效地避免了追踪航天器与目标航天器周围大型固定附件发生碰撞问题。但上述论文仅考虑了规划过程中的避障问题,忽略了实际工程中其他可能的约。文献[14]利用一种新型人工势函数与滑模技术结合的方法解决了路径约和视场约下的位置跟踪问题,同时考虑了航天器运动学耦合、未知扰动、运动约和输入饱和问题。文献[15]研究了一种基于θ-D的三维非线性最优控制技术,设计了一种闭环控制律。该控制律可以同时减小相对位置和姿态的跟踪误差以及柔性结构的振动。文献[16]中提出了一种鲁棒自适应控制器,采用基于范数估计的自适应方法处理目标惯性参数未知引起的动态耦合效应。文献[17]提出了一种基于特征模型的对接控制方法,克服了对接过程中追踪航天器配有较大帆板时所产生的挠性问题。另外,滑模控制器[18-19]和自适应模糊控制器[20-21]也被广泛用于航天器交会对接控制中。文献[22]中提出了一种基于神经网络的自适应滑模控制器,将滑模控制与神经网络逼近相结合,采用径向基函数(Radial basis function, RBF)神经网络对系统未知部分进行自适应逼近。然而,多数文献存在以下不足:1)忽略了追踪航天器与目标间相对位置与姿态的耦合关系,尤其对于翻滚目标,追踪航天器的期望位置与姿态间存在联系,必须进行统一的姿态轨道控制;2)在对追踪航天器进行规划控制的过程中,仅考虑避障或视觉系统视场,而没有对整个对接过程进行完整的约分析。

针对微纳卫星的对接任务还未在轨实践,且很少有论文涉及其控制问题。文献[23]介绍了美国CPOD任务的主体情况和控制策略,但没有对其中涉及的技术细节进行描述。文献[24]提出了一种针对参数不确定的离散线性系统的采样随机模型预测控制算法,并在气浮实验台上对该算法进行了验证。文献[25]提出了一种用于微纳卫星交会对接的基于H∞的鲁棒控制器,采用μ-Synthesis方法提高了控制器的鲁棒性。文献[4]提出了一种立方星姿轨跟踪翻滚目标的并发控制器,利用动量轮系进行立方星姿态调整控制,仅配备单轴推力器做轨道调整。但以上论文均忽略了对接过程中的安全问题及光学设备视场约问题。实际上,对于微纳卫星与非合作翻滚目标对接控制问题,不仅需要考虑其位置跟踪问题,也要考虑与翻滚目标对接端口的姿态同步问题。同时,微纳卫星所携带的推进设备通常在毫牛级别,需要考虑输入饱和问题,以及为了保证对接的安全性,应该对安全接近走廊提出约并对接近速度作出一定的限制,以保证危险发生时能够及时进行“刹车”等操作。另外,需要考虑追踪星光学设备的视场约,保证导航系统对目标的可见性。

模型预测控制(Model predictive control,MPC)是一种可以用于处理动态系统的高度非线性以及系统约的有效控制方法,其在控制工程领域有着悠久的历史。MPC策略具有许多优点,如滚动优化、显式处理约的能力以及适用于求解多变量优化问题,适用于本文提出的非线性约控制问题。在过去几年中,有部分学者将模型预测方法用于处理近距离对接约问题,文献[26]基于MPC策略设计了大型非合作航天器对接的位置控制对接器,但其忽略了航天器姿态同步控制问题。文献[27]设计了基于MPC的大型航天器交会对接的圆形及椭圆轨道的姿轨耦合控制器,但没有考虑接近目标过程中的路径约问题。文献[28]采用跟踪模型预测控制方法设计了立方星对接控制器,但其目标为相对静止目标,只考虑追踪星位置跟踪问题,没有考虑翻滚目标对接中的姿态同步问题,其控制器对于空间翻滚目标并不适用。另外,其约考虑并不全面,仅考虑了推力幅值约以及安全接近走廊约。

针对上述问题,本文针对微纳卫星与非合作翻滚目标对接控制问题,建立了六自由度姿轨耦合动力学模型,为了实现安全对接,充分考虑对接过程中可能存在的工程实际约,包括输入饱和约、速度约、追踪星视场约及安全接近走廊等约,提出了一种基于MPC的鲁棒非合作目标对接控制器,实现了微纳卫星对接非合作翻滚目标的姿轨一体化控制,为微纳卫星与非合作翻滚目标的对接提供了技术方案。

1 系统动力学

本文研究的场景是微纳卫星主动与非合作目标自主对接的最后阶段。目标是一个翻滚的非合作航天器或空间碎片,存在位置和姿态两种运动变化。假设可以通过探测获取追踪星与目标间的相对位置、相对速度、相对姿态及相对角速度等状态信息[29-31]。在存在约的情况下,追踪星从百米距离接近目标。在此超近距离下,目标在视觉相机中较大,不能将目标视为质点。考虑相对姿态与相对轨道动力学间存在耦合效应,本节首先建立六自由度追踪星与目标间的姿轨耦合相对动力学模型。

1.1 坐标系定义

为了建立追踪星和目标之间的相对运动模型,定义了下列坐标系,见图1。

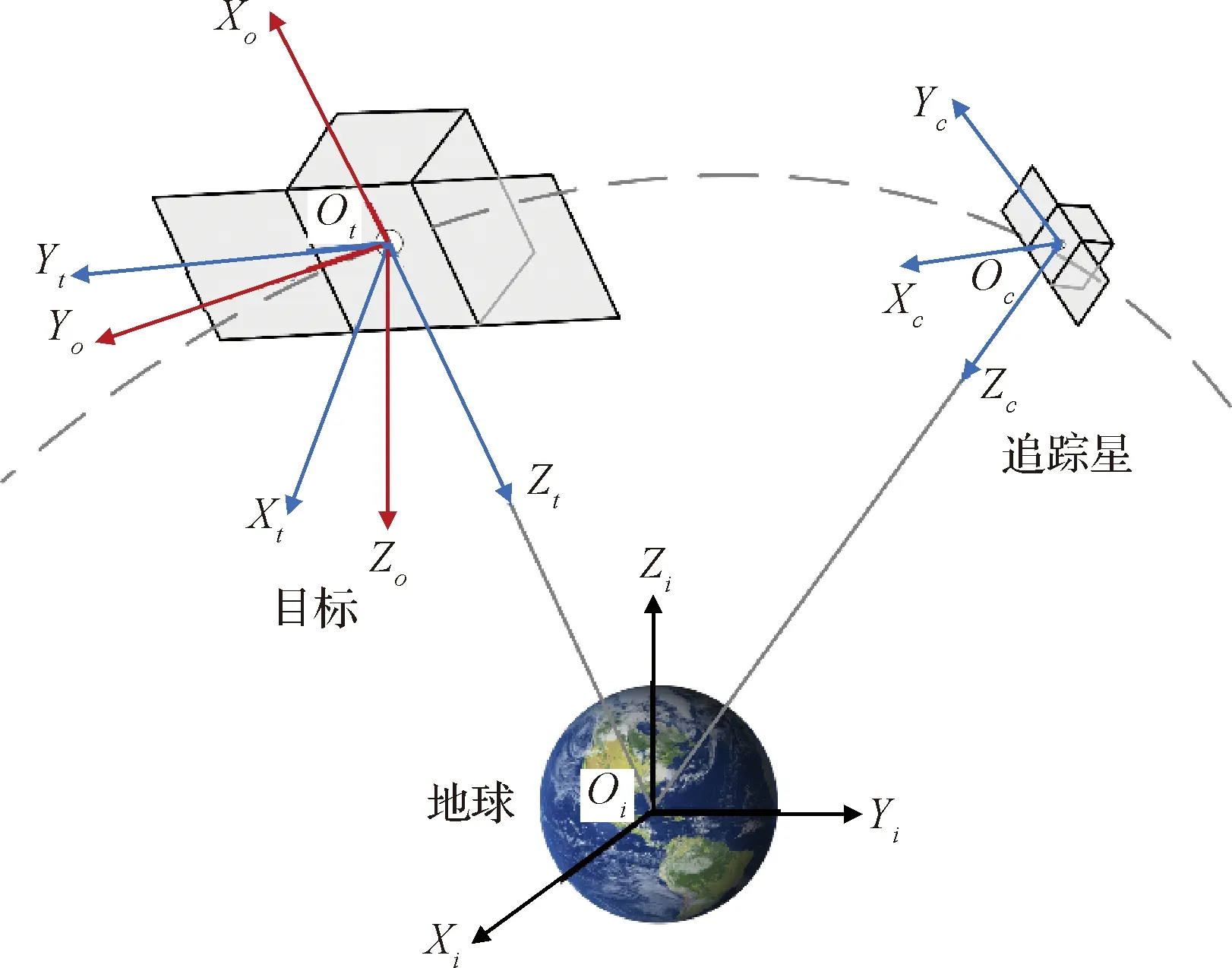
图1 坐标系定义Fig.1 Coordinate frames

1)地球惯性坐标系Fi:其原点在地心,Xi轴指向春分点,Zi轴垂直于赤道面指向北极,Yi轴由右手定则确定。

2)目标轨道坐标系Fo:其原点在目标质心,Xo轴与目标位置矢量rt重合,由地心指向目标,Yo轴在目标轨道面内与Xo轴垂直,沿目标运动方向为正,Zo轴垂直于轨道平面,与Xo轴、Yo轴构成右手坐标系。

3)体坐标系Ft:OtXtYtZt及Fc:OcXcYcZc:其原点分别位于目标及追踪星质心,Xk轴、Yk轴、Zk轴(k=t/c)分别与其惯性主轴重合。

1.2 相对轨道动力学模型

追踪星相对于目标的相对轨道动力学模型在Fo下可以表示为

(1)

式中:rc和rt分别为追踪星及目标星质心与地心之间的距离;mc表示追踪星质量;fdc=[fdxfdyfdz]T为在Fo坐标系下的未知有界相对摄动加速度;Fc=[FxFyFz]T为在Fo下的作用在追踪星上的控制力;其中ρ=[xyz]T表示Fo坐标系中两者的相对位置;μ表示地球引力参数,取μ=398600.5 km3/s2;θ代表目标的真近点角。假设目标处于近圆轨道,追踪星与目标间的距离较小,即||ρ||≪rt,可以将式(1)线性化,则追踪星相对于目标质心的运动近似表达为

(2)

式中:

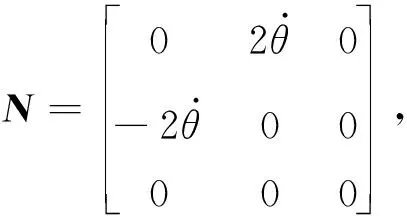
1.3 相对姿态动力学模型

本文采用修正型罗德里格参数(Modified rodr-igues parameters,MRP)描述追踪星与目标间的相对姿态运动。目标的绝对姿态动力学可以表示为:

(3)

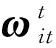
(4)

以惯性坐标系Fi作为参考坐标系,目标的姿态运动学可以表示为

(5)

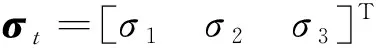
(6)

式中:Ir∈Rr×r表示一个r维单位矩阵。

同理,将追踪星姿态动力学和运动学方程描述为

(7)

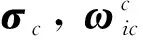
(8)

式中:Rct为目标体坐标系Ft到追踪星体坐标系Fc的坐标转换矩阵,可由σct根据下式得到

(9)

式(8)对时间求导可得

(10)

结合式(3), (5), (7)可得,追踪星与目标的相对姿态动力学与运动学方程可以表示为

(11)

式(11)中矩阵Td,P,Q分别为

(12)

1.4 六自由度姿轨耦合动力学模型

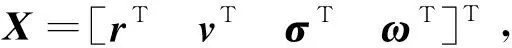
AX+BU+d

(13)

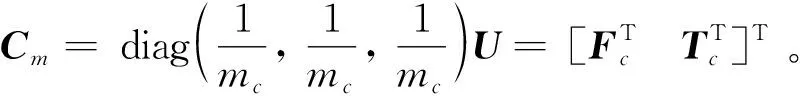
(14)

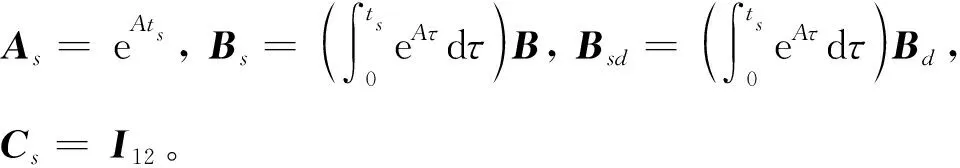
2 控制器设计

MPC控制方法可以将最优控制问题转化为在线数值求解优化问题,能够大幅降低计算复杂度,并且可以处理各种控制输入约及状态量约。因此,本节主要推导系统的状态空间模型,建立输入量及状态量约并设计目标函数,利用MPC方法求解有约的非线性最优控制问题。

2.1 控制目标

控制的最终目标是追踪星能够实现对目标的位置追踪和姿态同步。具体表现为在抵近的过程中,即使目标处于翻滚状态时,追踪星对接端口始终保持与目标对接端口对齐,接近目标对接端口并到达指定对接位置。

相对位置控制的目标是保持追踪星与目标对接轴的视线指向,并最终转移到与目标对接的位置。在此过程中追踪星在坐标系Fo下的期望相对位置矢量rd、相对位置误差er和相对速度误差ev可以表示为

(15)

由于目标处于不受控的翻滚状态,因此,对接端口位置实时变化,追踪星的期望姿态也在实时变化,姿态控制的目的是消除期望端口位置与当前方位的姿态误差,使得追踪星沿对接轴方向接近端口,保证追踪星与目标的姿态同步。

则追踪星与目标间期望相对姿态为

(16)

2.2 约模型

追踪星接近目标直至对接的过程中,需要考虑一系列实际的工程约,以保证对接的安全性与稳定性。将约分为两类,一类为控制量约,主要为控制饱和约;另一类为状态量约,包括接近目标过程中的速度约、安全接近走廊约、追踪星视场约等。

(1)控制饱和约

在实际工程中,星载推力器的能力是有限的,尤其是以微纳卫星作为载体时,推力器所提供的推力通常只有毫牛级,必须对控制输入进行限制,具体可将输入饱和约表述为

(17)

式中:Fmax为星载推力系统能提供的最大力;Tmax为星载推力系统能提供的最大力矩。

(2)速度约

如果要进行超近距离作业,应该考虑速度限制。如果在这个过程中发生了紧急情况,必须在很短的时间内改变预定的交会轨道,从而确保不会发生碰撞。在本文中,速度约描述如下

(18)

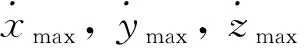
ΓX≤Vlim

(19)

式中:

式中:0m×n表示一个m×n维的零矩阵。

(3)安全接近走廊约

追踪星应遵循安全路径,以避免在接近过程中与目标或其帆板等可展开附件发生任何意外碰撞。将安全接近走廊定义为以目标对接端口为原点,以对接端口中心轴为轴线的圆锥体。坐标系Fp:OpXpYpZp表示对接装置安装坐标系,坐标原点位于对接端口中心,对接装置安装在目标-Xp轴上,假设Xp轴与Xt轴重合。实际上,Xp轴与Xt轴不一定重合,只需要将约方程做相应的坐标转换即可。将安全接近走廊约表述为

-xp 0lt≥||lt||cosβ

(20)

式中:lt表示Ft系下目标对接装置与追踪星间的相对位置矢量;xp 0表示Ft系下Xt轴的单位矢量;β表示安全接近走廊旋转轴最大角度。

式(20)可以表示为

-xp 0Rtor≥||lt||cosβ

(21)

式中:Rto为轨道坐标系Fo到目标体坐标系Ft的坐标转换矩阵,表示将其记为

ΞX≤hx

(22)

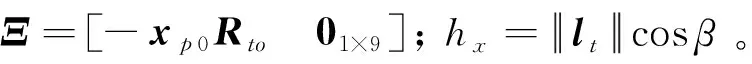
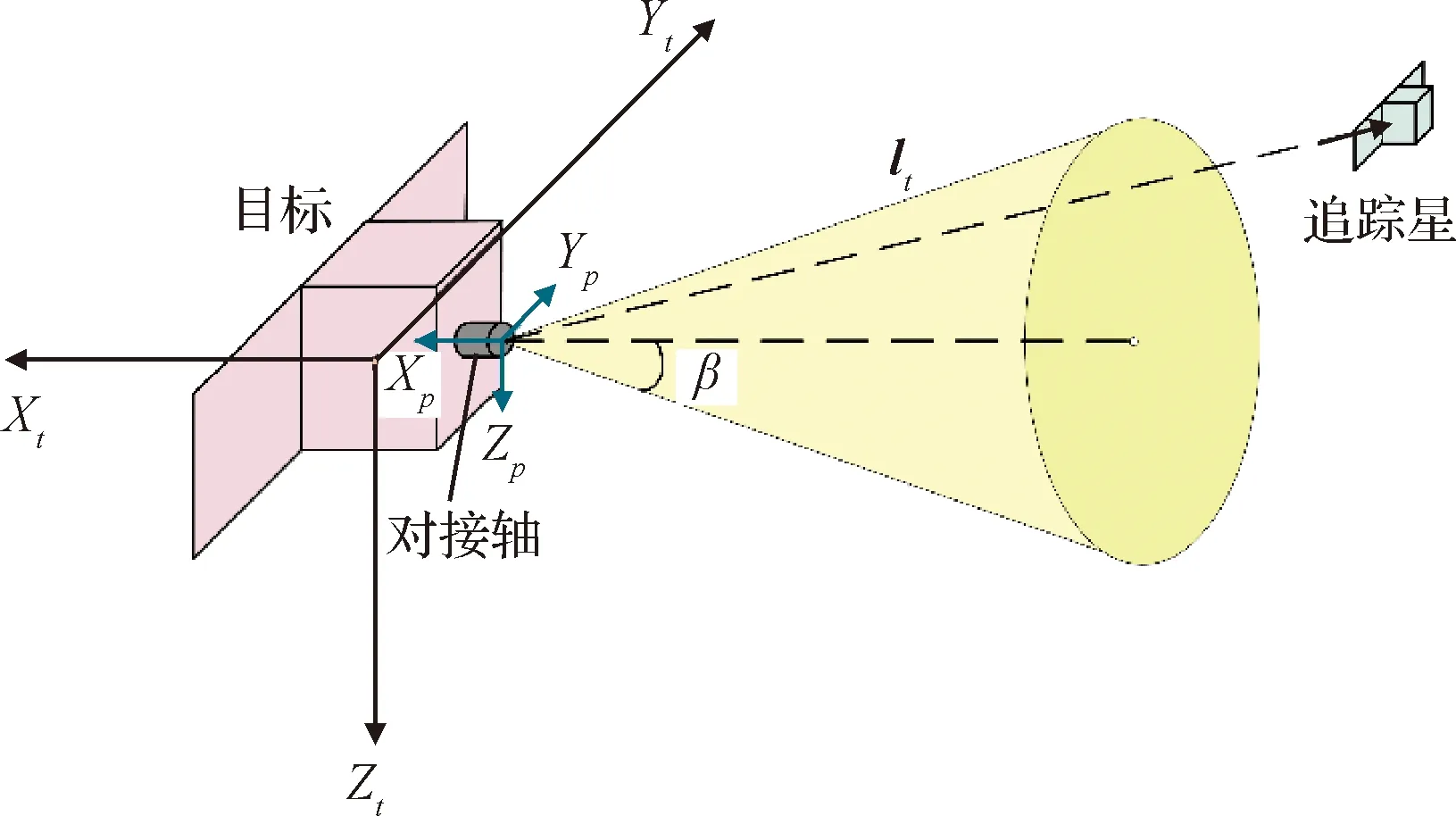
图2 安全接近走廊约示意图Fig.2 Illustration of approach corridor constraint

(4)追踪星视场约

交会对接操作的最后阶段很大程度上依赖基于视觉的相对测量,由于星载相机和激光测距仪等光学传感器的视野有限,因此在接近目标的过程中,要始终保持目标的对接端口在追踪星所携带光学设备的视场中。因此,本文假设视线锥体从追踪星上突出,要求对接端口始终保持在该视线锥体内以进行基于视觉的测量。本文假设光学设备视线坐标系Fs:OsXsYsZs(如图3)与坐标系Fc重合,在实际星上任务中,其安装位置不固定,只需要将约方程从Fs中转化到Fc系下即可。以矩形圆锥视轴建立约模型,在Fs(Fc)系下将其表示为

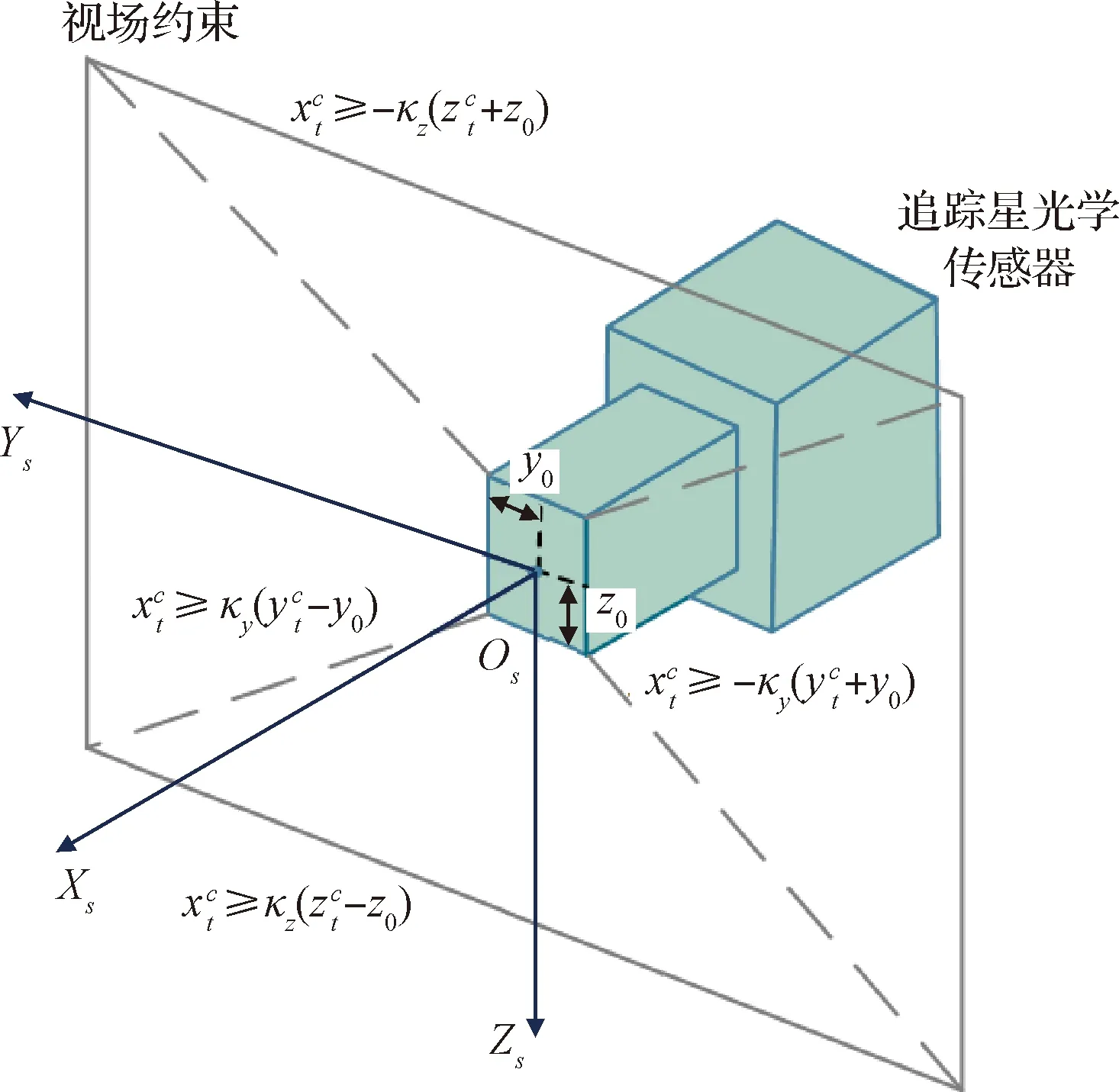
图3 视场约示意图Fig.3 Illustration of line-of-sight constraints

(23)

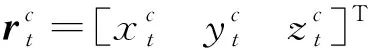
(24)

式中:

将式(24)中表示的约从Fc系转化到Fo系下,其中的变换可以定义为

(25)

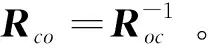
则追踪星视场约可以改写为

ΛX≤blos

(26)

2.3 MPC控制策略

在MPC控制过程中,每一步都要解决一个约优化问题,在最小化未来跟踪误差的加权平均值的同时考虑系统的控制约。因此,MPC的优化目标可以表述如下

Qj(YP(k+j|k)-Yd(k+j))+

(27)

假设在采样时刻k可以得到系统状态变量X(k)。其中,Yp(k+j|k),Yd(k+j), ΔU(k+j-1|k)分别表示在k时刻预测的系统在k+j时刻的输出、期望输出以及控制输入的增量。Qj及Rj分别表示状态量及控制增量的加权因子。Np为预测时域,Nc为控制时域。

引入向量

(28)

系统状态空间模型可以写为

(29)

式中:Sx∈R12Np;Yp∈R12Np;Su∈R6Nc,表述为

(30)

式中:“⊗”用来表示两个矩阵的克罗内克积[26]。

目标函数式(27)可以改写为

(31)

将控制输入约式(17)表示为

(32)

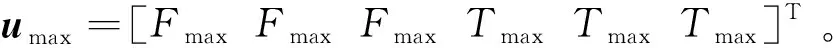
将式(32)记为

WuUp(k)≤wu

(33)

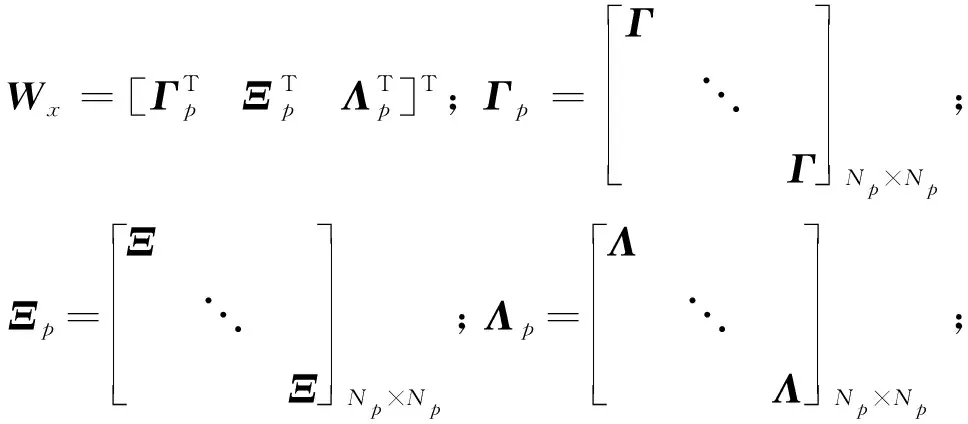
将状态变量约式(19)、(22)和(26)记为

WxXp(k)≤wx

(34)

MPC策略采用以后退方式解决最优控制问题,该问题基于系统状态空间模型式(29)、系统约式(33)、(34)及目标函数式(31),表述为

(35)

3 仿真校验

本节针对两种不同对接场景,对前述基于MPC的对接控制器进行仿真校验。第一种是相对较简单的情况,令追踪星接近一个非旋转的目标,在对接过程中仅考虑输入饱和约,用于验证控制器的有效性及处理控制饱和约的能力。第二种是较为复杂的情况,当微纳卫星与翻滚目标进行对接,考虑对接过程中的输入饱和约、速度约、追踪星视场约和安全接近走廊约,用于验证控制器对翻滚目标对接的有效性以及同时处理多种复杂约的能力。

在实际空间环境中,卫星始终受到空间环境各种摄动力和力矩的作用,包括地球形状非球形摄动、大气阻力、太阳光压等摄动力,以及重力梯度力矩、气动力矩等空间环境力矩。对追踪星增加干扰力及力矩,模拟太空真实环境,验证控制器具有处理外部干扰和模型不确定性的能力。将追踪星受到的干扰力和力矩描述为如下形式

(36)

3.1 与非旋转目标对接校验

在追踪星与非旋转目标对接的情况下,无论是相对位置、相对速度、相对姿态角及相对角速度的期望值都是恒定的。追踪星和目标的物理参数数值以及约参数如表1所示。控制参数选择为Np=5,Nc=5。为了说明本文所提出控制器的先进性,引入文献[19]所提出的滑模控制策略(Sliding mode control,SMC)进行比较,设置两者的物理参数及控制输入约相同。

表1 非旋转目标对接仿真主要参数Table 1 Main parameters of the simulation for docking with a non-rotating target

图4和图5分别给出了坐标系Fo中追踪星相对目标的相对位置误差及相对速度误差随时间变化的曲线。图6和图7给出了在坐标系Ft中追踪星相对目标的相对姿态和相对角速度的误差曲线。从图中可以看出,在存在相同初始误差,且执行机构所提供的力及力矩存在同等幅值约情况下,MPC控制器可以实现在200 s内到达期望对接位置,在50 s之内实现与目标的姿态同步,跟踪位置误差在1×10-3m之内,速度误差在1×10-4m/s之内,姿态同步误差在2×10-3之内,角速度误差在6×10-5rad/s之内。相比之下,SMC控制器达到目标的时间更长,精度更差,并且滑模控制方法会存在抖振问题,需要通过引入干扰观测器或改变趋近律等方法消除抖振。另外,由图4可以观察到,采用MPC控制器不会产生超调问题,而SMC控制器则存在超调现象,在工程实践过程中可能会导致追踪星与目标发生碰撞。MPC控制方法下的控制输入信号随时间变化曲线如图8所示,可以看到控制输入总是在预定的边界内,这表示控制策略具有处理控制饱和约的能力。因此,可以得出结论,所开发的MPC控制器能够实现对期望位置的有效停靠和对目标姿态的同步追踪,并且相比于一般的SMC控制器具有更好的性能。

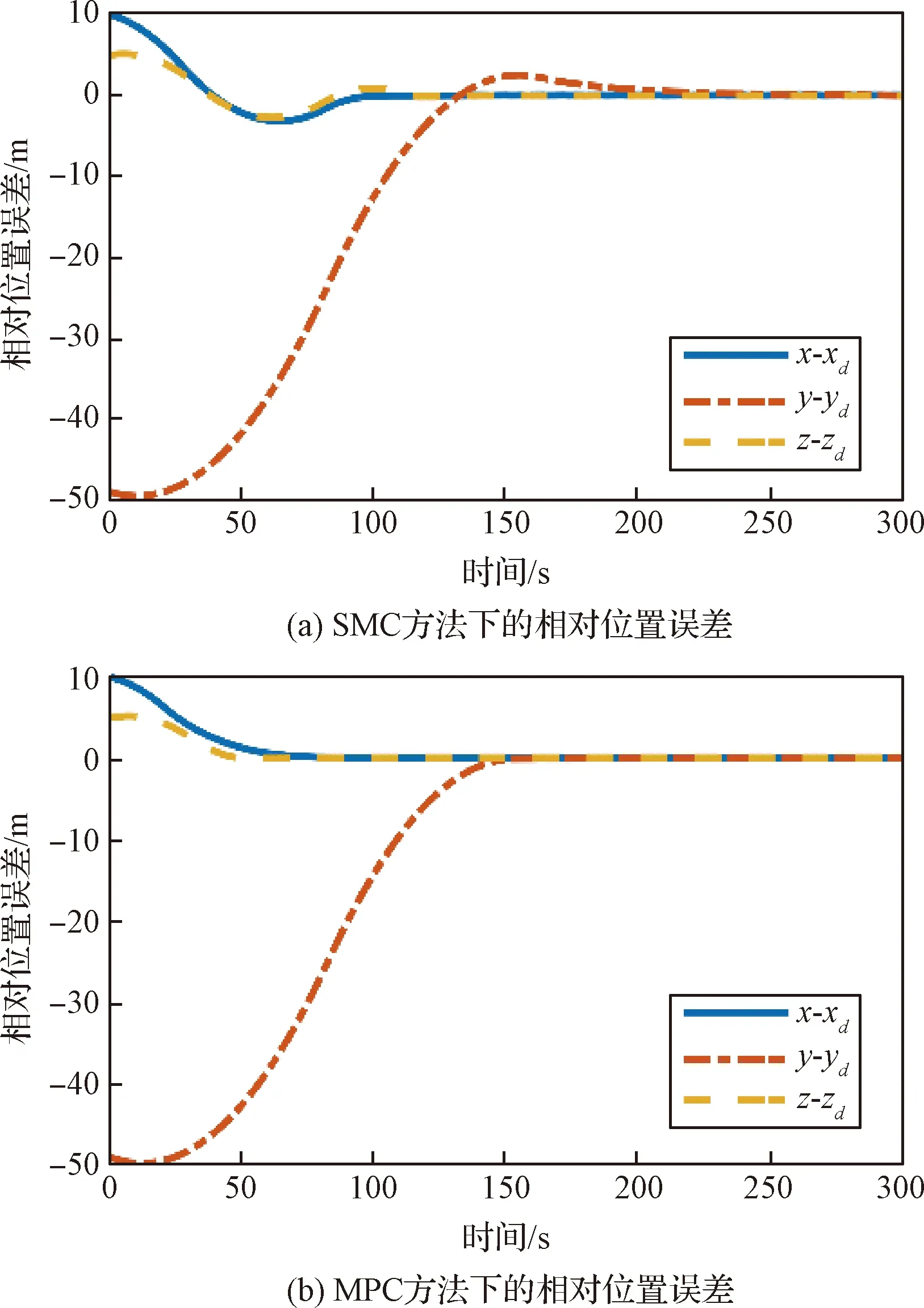
图4 位置误差随时间变化曲线Fig.4 Time response of the relative position error

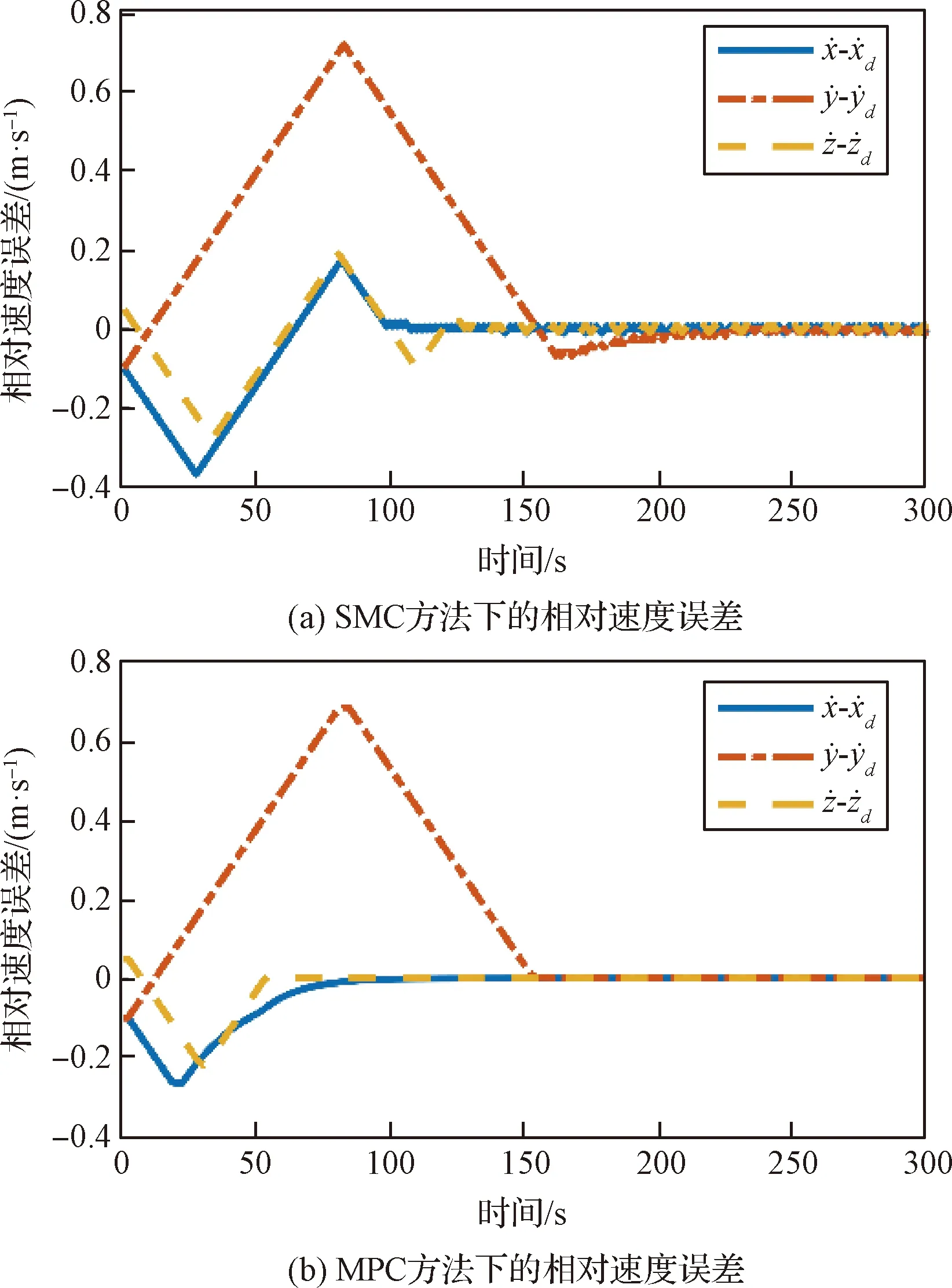
图5 速度误差随时间变化曲线Fig.5 Time response of the relative velocity error

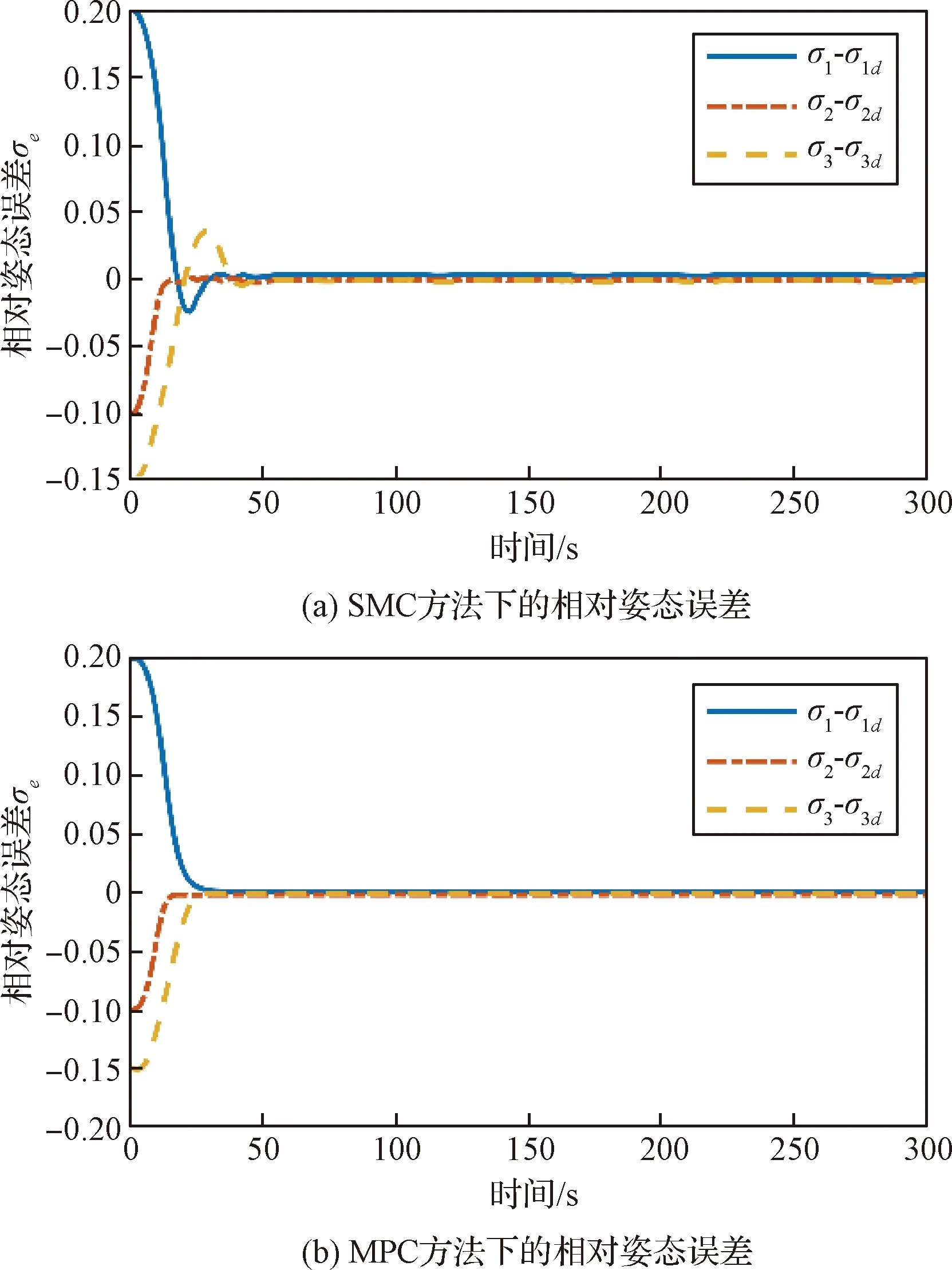
图6 相对姿态误差在追踪星体坐标系下随时间变化的曲线Fig.6 The relative attitude error in the chaser spacecraft body frame

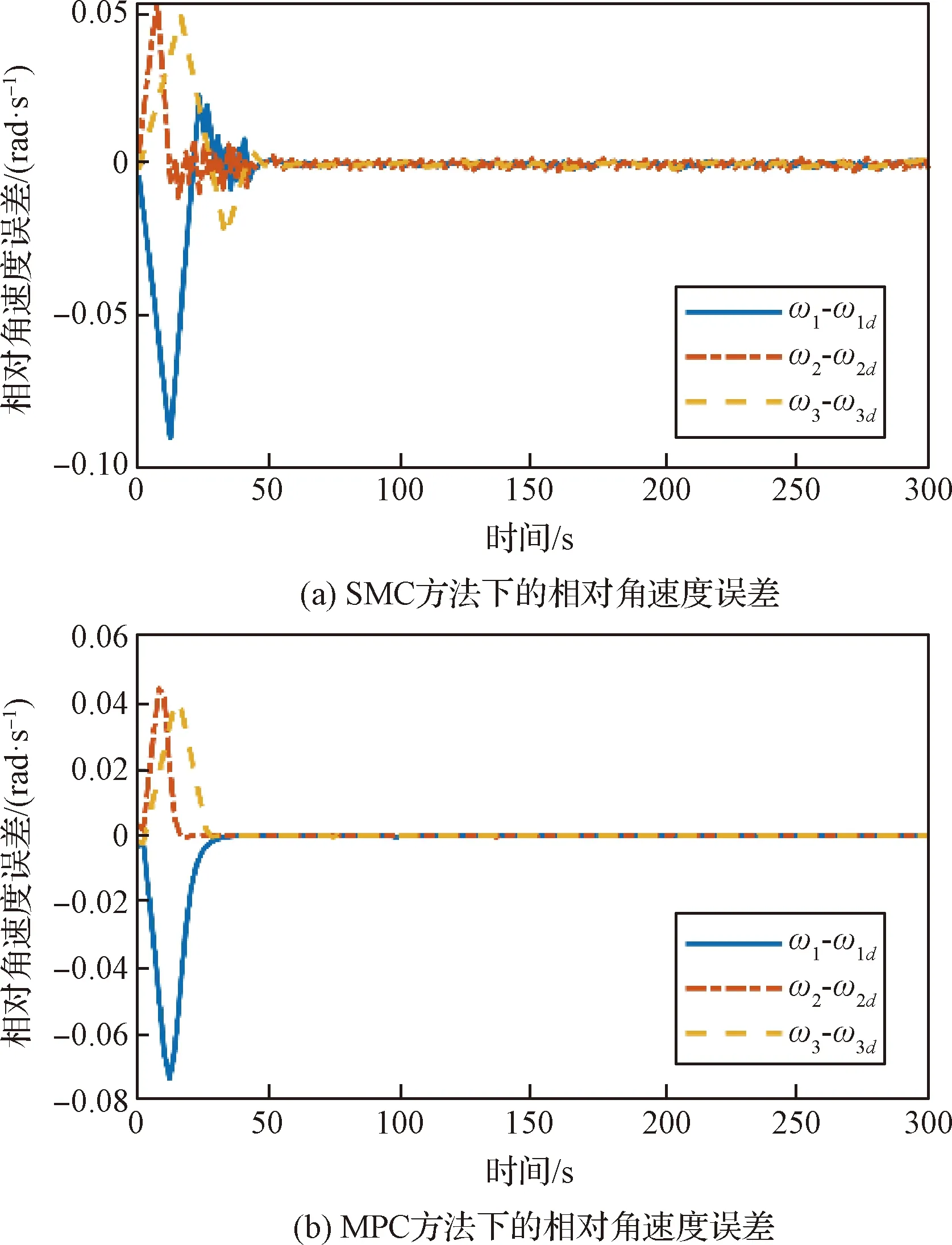
图7 相对角速度误差在追踪星体坐标系下随时间变化的曲线Fig.7 The relative angular velocity error in the chaser spacecraft body frame

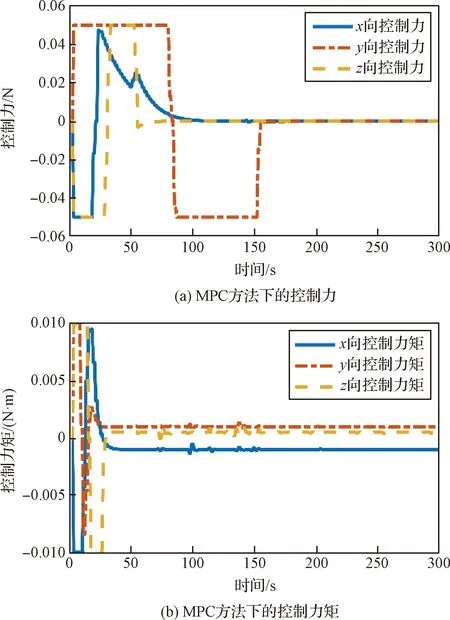
图8 MPC方法下控制输入随时间变化的曲线Fig.8 Time response of control input under MPC

3.2 在多约情况下与翻滚目标对接校验

在此场景下,令追踪星追踪一个动态翻滚目标,该目标存在一定的初始角速度并受到一定的干扰力矩(物理参数如表2所示)影响。在此情况下,期望位置、相对速度、相对姿态及相对角速度均为时变量。追踪星和目标的物理参数数值以及约参数如表2所示。另外,半长轴、追踪星质量,两者的转动惯量及目标对接轴参数与3.1小节相同。控制参数选择为Np=5,Nc=5。

表2 翻滚目标对接仿真主要参数Table 2 Main parameters of the simulation for docking with a tumbling target

仿真结果如图9～13所示。图9～11分别给出了追踪星实际状态量与期望状态量随时间变化的曲线,分别为相对位置、相对速度、相对姿态变化情况。从图中可以注意到,尽管在目标翻滚情况下,控制器依旧在300 s内到达期望对接位置,100 s内实现对目标的姿态同步,之后保持对目标姿态的追踪。位置跟踪误差在0.04 m之内,速度误差在2×10-3m/s之内,姿态同步误差在5×10-3之内,角速度误差在6×10-3rad/s之内。

另外,可以从图5中观察到,在与相对静止目标对接时,追踪星y向速度分量达到了0.7 m/s。在实际对接操作过程中,应该尽量保持速度在一个较小的范围,这样可以保证紧急情况下有足够的时间对卫星进行相应的调整。从图10可以观察到,在增加速度增量约后,y向速度分量始终在约量0.5 m/s之内,可以认为所设计的控制律能够有效地处理速度约。从图9可以观察到追踪星与目标对接轴之间的相对距离始终大于预定的边界距离,以及在图12中,接近目标对接轴的角度始终保持在边界值60°以下,满足安全接近走廊约。因此可以认为所设计的控制律能满足避碰需求。在图13中可以观察到目标在追踪星视线坐标系下的相对路径始终在追踪星光学设备的视场约之内,保证了追踪星对目标的持续可观性。

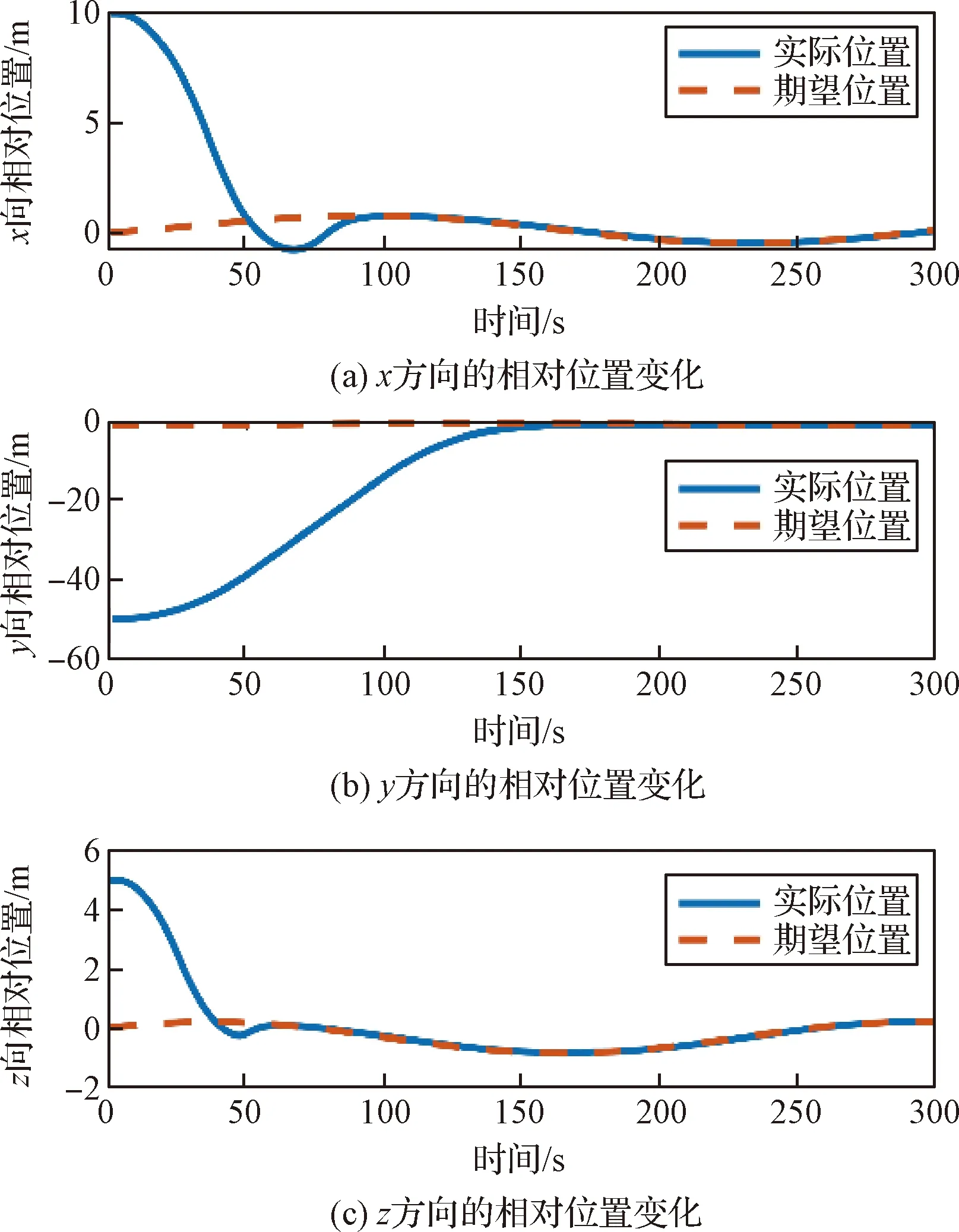
图9 相对位置随时间变化曲线Fig.9 Time response of the relative position

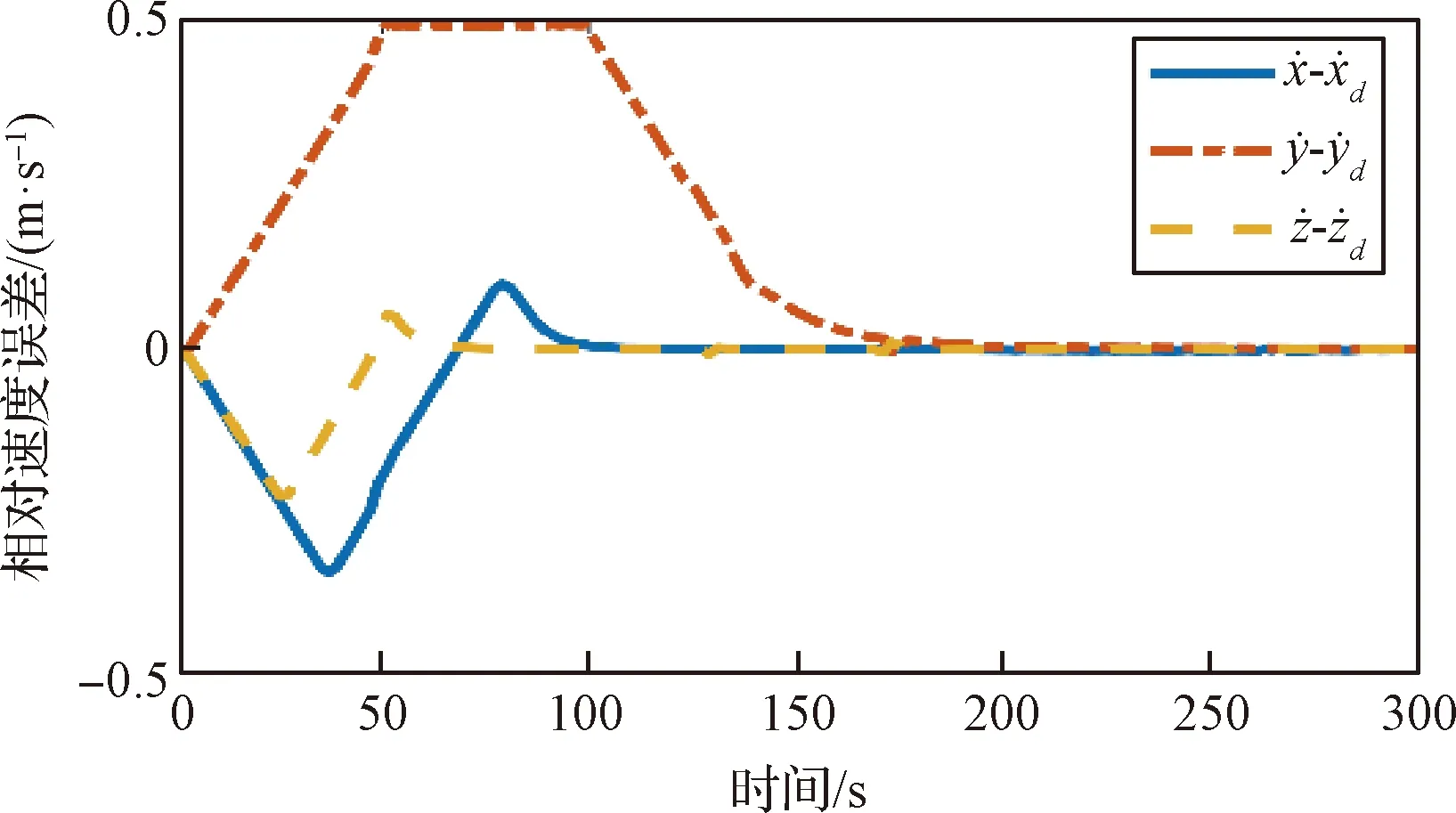
图10 相对速度误差随时间变化曲线Fig.10 Time response of the relative velocity error

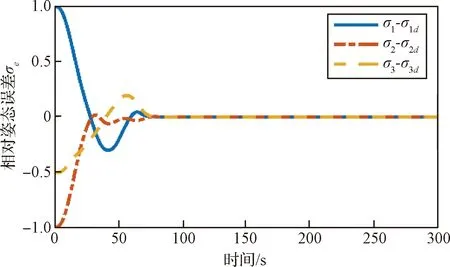
图11 相对姿态误差在追踪星体坐标系下随时间变化曲线Fig.11 Time response of the relative attitude error in frame Fc

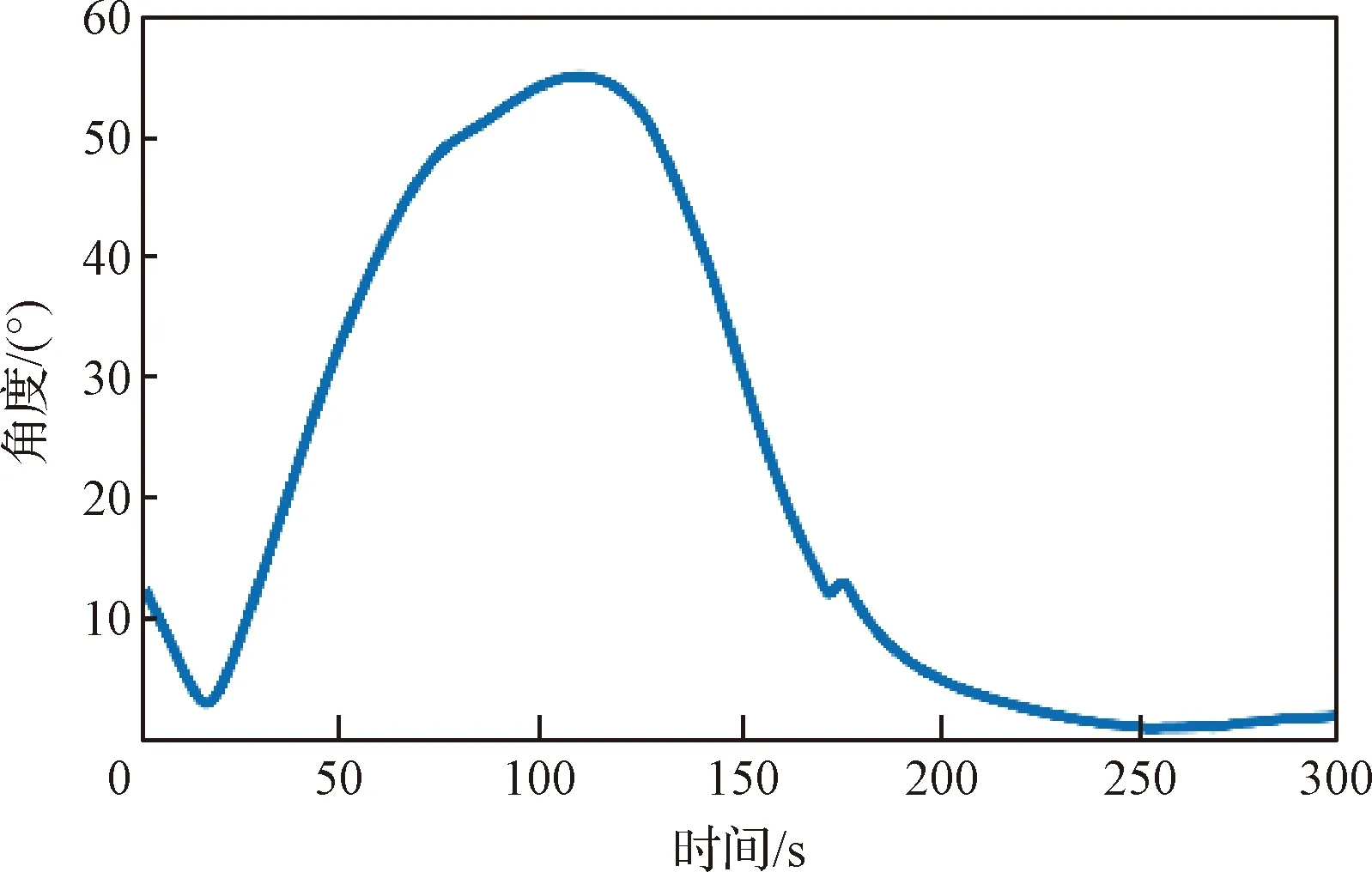
图12 与目标对接轴夹角随时间变化的曲线Fig.12 Time response of the approach angle

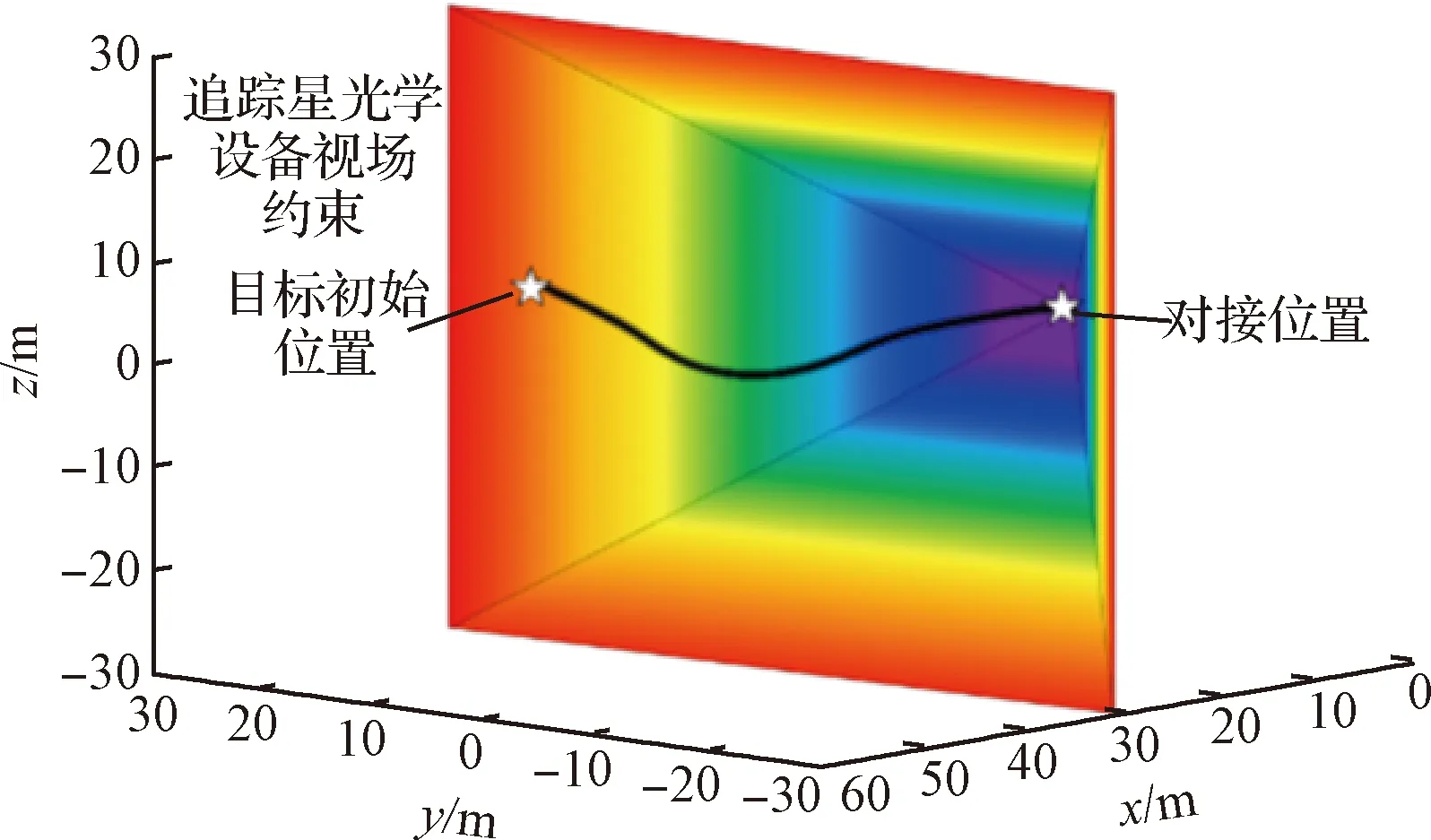
图13 三维对接轨迹图Fig.13 3D docking trajectory diagram

4 结 论

本文针对微纳卫星与非合作翻滚目标交会对接过程中的控制问题,面向位置跟踪与姿态同步过程,结合姿态与轨道动力学耦合关系及MPC控制策略,充分考虑控制输入饱和约、速度约、追踪星视场约以及安全接近路径约等一系列工程实际约,完成了多约下微纳卫星与非合作翻滚目标对接器的设计。在此基础上,针对不同的对接场景,评估所开发MPC控制器的有效性和鲁棒性。仿真校验结果说明本文所设计的MPC控制器能够有效实现与翻滚目标的位置跟踪与姿态同步。相比于一般的SMC控制器,本文提出的MPC控制器具有更高的精度,并且无超调现象发生。当目标为翻滚目标时,MPC控制器的位置跟踪误差在0.04 m之内,速度误差在2×10-3m/s之内,姿态同步误差在5×10-3之内,角速度误差在6×10-3rad/s之内。另外,其能够有效保证追踪星在接近目标过程中同时满足所提出的系统约,保证了安全和视觉测量要求,并具有处理控制饱和约的能力。同时,控制器可以较好地处理外部扰动引起的不确定性以及非线性动力学形式的模型不确定性,具有较好鲁棒性。