运载火箭与航天器界面载荷设计优化方法
2023-04-15曾耀祥
何 巍,曾耀祥,刘 晖
(北京宇航系统工程研究所,北京 100076)
0 引 言
运载火箭在跨声速飞行时,受到脉动压力等外激励影响[1],火箭及搭载的航天器会产生明显的动态加速度和内力响应。动态内力是航天器主体结构、火箭适配器、器箭连接装置等航天器内分支结构设计的重要输入条件,而准确合理地给出动态内力设计值能有效降低非必要结构重量、有效提升有效载荷质量,对提升器箭结构效率和整体设计性能有着十分重要的意义。
国内外火箭用户手册中以航天器质心等效加速度的形式规定器箭界面载荷条件,根据航天器质量、质心高度以及质心加速度位置则可计算得到界面力及界面力矩。目前大多数火箭用户手册中,该条件对于任意航天器均取相同值[2-4],根据动力学理论,航天器质量、质心及基频等质量与频率特性必然会对动态内力响应产生影响,而当前的载荷设计条件未考虑航天器特性的影响。近些年,部分火箭的用户手册开始依据不同的航天器参数区间给出界面载荷条件,宇宙神5火箭和“质子”火箭针对不同的航天器质量范围(按照是否大于3175 kg进行划分)给出了不同的横向质心等效过载;同样,猎鹰9火箭按照航天器质量是否大于1814 kg给出不同的横向质心等效过载,不同区间对应的横向质心等效过载最大差异可达100%,但用户手册中未对划分依据进行说明[5-7]。由于动态内力随自身特性参数变化规律的复杂性,需要开展深入研究。
器箭组合体动力学模型复杂,直接通过理论分析研究质心等效加速度的变化趋势十分困难,考虑到器箭组合体属于长细比很大的薄壁结构,符合梁模型动力学基本假设,因此可基于梁动力学理论分析航天器分支特性参数对质心等效加速度的影响规律[8-10]。对于连续梁,其固有频率的影响因素有截面形状、约条件、材料及分段杆长等[11-14],李顺才等[15]、黄志杰等[16]针对不同边界条件下的连续梁振动进行了研究,提出了对应的微分方程形式,对固有频率以及振型等振动特性进行了理论求解,而器箭组合体实际为多分支梁结构,其动态响应的理论解还需进一步研究。
简化的梁动力学模型可用于定性分析质心等效加速度与不同参数间的关联,但当前对质心等效加速度较为准确的计算还依赖于器箭动力学耦合分析,该方法经过逐渐发展,目前已形成成熟工具软件[17-20]。郭峰等[21]研究了有效载荷基频变化对火箭点火起飞时刻动响应的影响,结果表明基频降低会显著增加轴向过载,但未对横向过载变化进行研究,未涉及其他特性参数。
本文基于分支梁动力学理论,构建了器箭组合体的简化模型,对横向激励作用下的横向质心等效加速度进行了理论分析,基于理论解析式,辨识了主要影响因素,并研究了横向质心等效加速度与航天器质量、质心高度以及基频等因素的相关性以及变化规律。同时,采用耦合分析方法,系统获取了跨声速阶段不同航天器参数组合下的横向质心等效加速度,结合理论分析规律,对横向质心等效加速度分布开展进一步分类统计分析,提出了一种可行的器箭界面动态内力精细化设计思路及方法。
1 器箭界面动态内力影响因素分析
火箭跨声速飞行时,激励一般作用在整流罩前锥与柱段连接点位置。因此,可通过施加横向单频激励,基于简化的分支梁动力学理论,推导横向质心等效加速度求解理论方程组,基于理论方程组对质心等效加速度随航天器质量、质心高度以及基频等参数的变化规律进行系统研究。
1.1 器箭组合体分支梁模型
器箭组合体结构可以划分为三个部分,分别为箭体结构、整流罩以及航天器(有效载荷)。考虑到器箭组合体的长细比较大,可以近似用梁模型动力学基本理论进行分析,梁模型如图1。

图1 器箭组合体简化梁模型Fig.1 Simplified beam model of the combination of rocket and spacecraft
其中1~3均为等直梁,1代表火箭箭体(不包含整流罩),2代表整流罩,3代表航天器,虚线框表征器箭界面,三段梁在该处具有共同的节点。在2号梁的右端点即整流罩头部施加频率为为ωF、幅值为F的单频横向外激励模拟火箭在跨声速飞行阶段的横向脉动压力。
构建器箭组合体简化模型后,基于梁振动理论,即可对航天器质心等效加速度ac表达形式进行理论推导。
1.2 航天器质心等效加速度理论求解
火箭飞行过程处于自由状态,因此首先考虑等直梁的自由振动方程:
(1)
式中:yi表征i号梁的横向位移;x代表i号梁上各点坐标;Mi,Li分别为i号梁的质量及长度;Hi代表i号梁的弯曲刚度(EJ)i。
对式(1)频响形式解进行求解,即梁振动频率与外激励频率一致,也即认为梁的横向位移满足如下形式:
yi(x,t)=yi(x)exp(jωFt)
(2)
将式(2)中的横向位移形式代入式(1)中,则可以求解得到频响形式解为
(3)
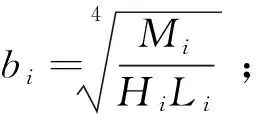
对图1中模拟器箭组合体的分支梁模型,取器箭连接面处为坐标原点,考虑到简化模型为线性系统,取单位外激励对该系统开展分析。
根据结构力学理论,等直梁转角、弯矩以及剪力可由横向位移曲线确定,即:
(4)
对于器箭组合体分支梁模型,火箭(1号梁)及航天器(3号梁)为自由边界,即弯矩与剪力为0;而整流罩由于头部施加横向外激励,因此边界处弯矩为0,而剪力则等于施加的横向外激励。则动力学方程边界条件如下:
(5)
考虑到器箭界面处位移及转角需要满足变形协调条件,界面处可建立以下方程:
(6)
另,考虑界面处平衡条件,即连接面两侧弯矩及剪力需互相平衡,可建立以下方程:
(7)
以上方程构成了器箭组合体系统三段等直梁的各4个非齐次线性方程组,将横向位移代入方程,对以上方程组进行求解,可得到器箭界面弯矩:
(8)
考虑横向质心等效加速度计算公式,记航天器质量为m,质心高度为h,横向质心加速度可通过界面弯矩换算得到:
(9)
将航天器简化为等直梁,M3=m,L3=2h,最终可得到横向质心等效加速度表达式为
(10)
λ1~λ8为与航天器特性(质量及质心高度)无关的参数,具体形式如下:
(11)
其中p0~p4与航天器基频相关,称为频率参数,而ξ1~ξ8只与箭体结构与外激励频率相关,称为箭体参数,两组参数的具体形式分别见式(12)和(13)。
(12)
(13)
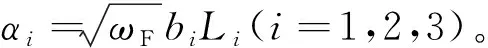
1.3 航天器质心等效加速度变化规律研究
根据动力学理论分析得到的航天器横向质心等效加速度表达式(10),横向质心等效加速度与有效载荷、箭体结构形式以及外激励特性均有关系,考虑到对于特定型号的火箭,箭体结构形式相对固定,同时外激励形式经过多次飞行验证,因此重点研究不同频率外激励作用下航天器质量、质心高度以及基频对横向质心等效加速度的影响。本文选定某型整流罩、火箭及航天器等效参数开展研究,具体参数见表1。

表1 整流罩及火箭参数Table 1 Fairing and rocket parameters
由于质心等效加速度的变化趋势十分复杂,以随质量的变化为例,不同外激励和器箭组合体参数下,质心等效加速度可能呈现完全不同的变化趋势。因此本文定义了趋势指数以更好地描述质心等效加速度随不同参数的整体变化规律。以下对趋势指数进行简要介绍。
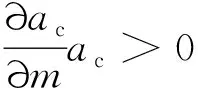
1.3.1航天器质量对质心等效加速度的影响
为了更直观地研究航天器质量对横向质心等效加速度的影响,在选定若干航天器基频及质心高度参数组合下分析横向质心等效加速度随质量的变化规律,基频分别为30 rad/s, 90 rad/s, 150 rad/s,对应质心高度分别为1 m, 3 m, 5 m。
图2~图4为航天器不同质心高度以及基频组合下质心等效加速度变化趋势指数随外激励频率及质量变化的二维分布图。
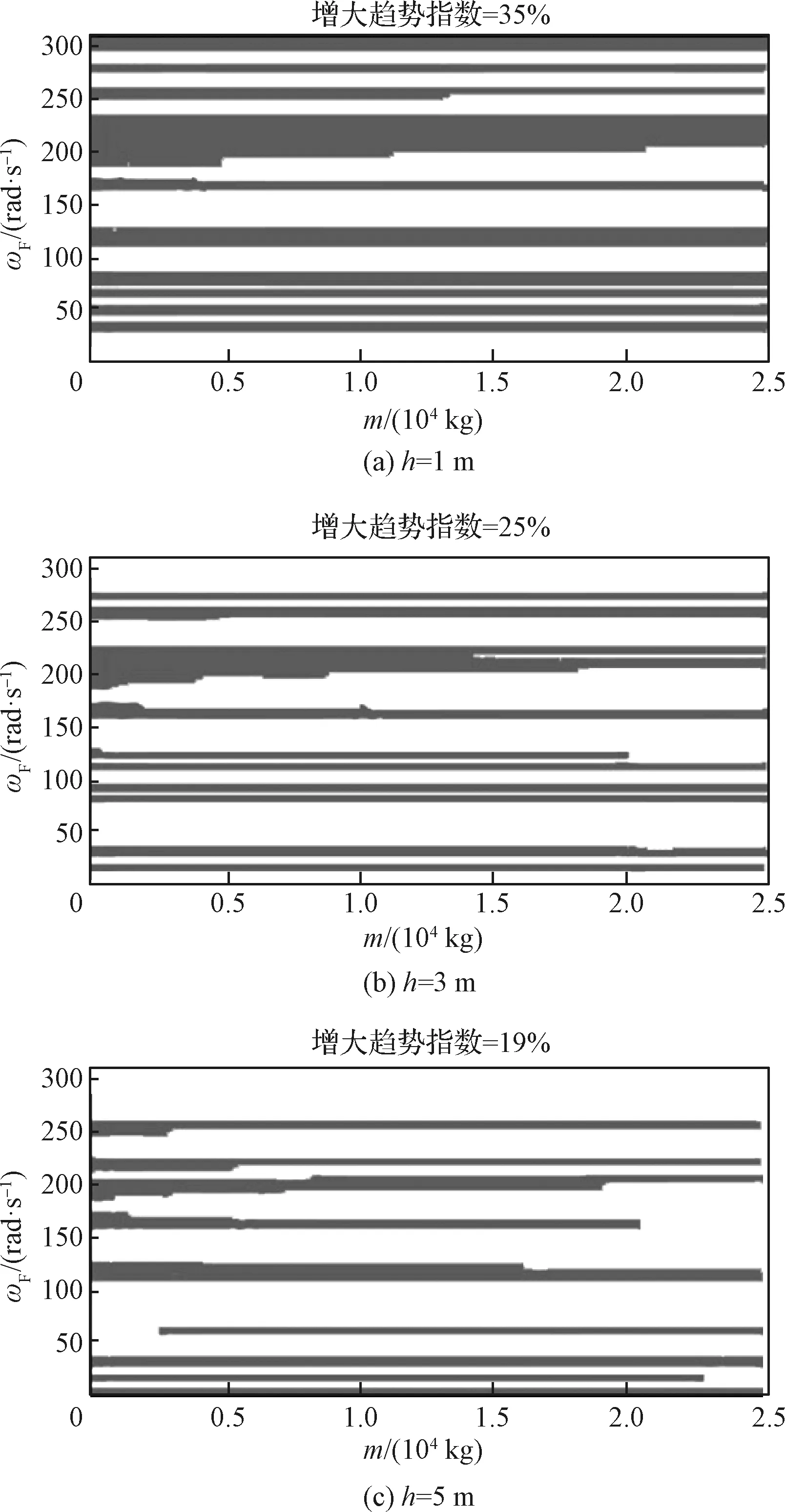
图2 趋势指数随外激励频率及质量分布(ω=30 rad/s)Fig.2 Distribution of trend index on frequency of external excitation and mass (ω=30 rad/s)
根据分析结果,对于各参数组合,尽管不同的外激励频率作用下,横向质心等效加速度随航天器质量的变化规律存在差异,但横向质心等效加速度关于外激励频率ωF与航天器质量m的分布图中均以白色区域占主要部分,占比均在65%以上,即横向质心等效加速度与航天器的质量有明显的相关性,随着航天器质量增加其有显著的下降趋势,并且随着质心高度的增加,横向质心等效加速度随航天器质量而降低的趋势逐渐增强。
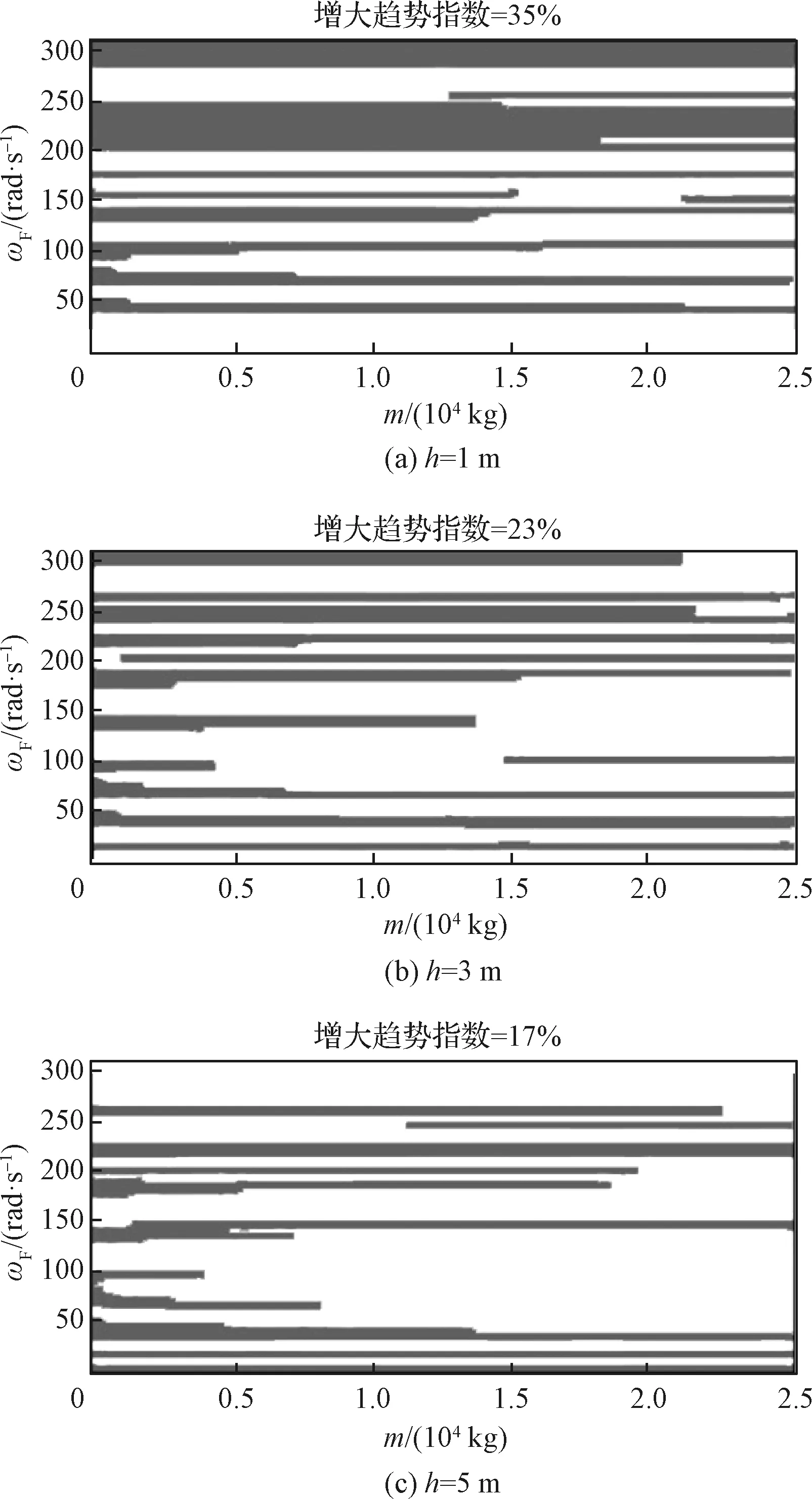
图3 趋势指数随外激励频率及质量分布(ω=90 rad/s)Fig.3 Distribution of trend index on frequency of external excitation and mass (ω=90 rad/s)
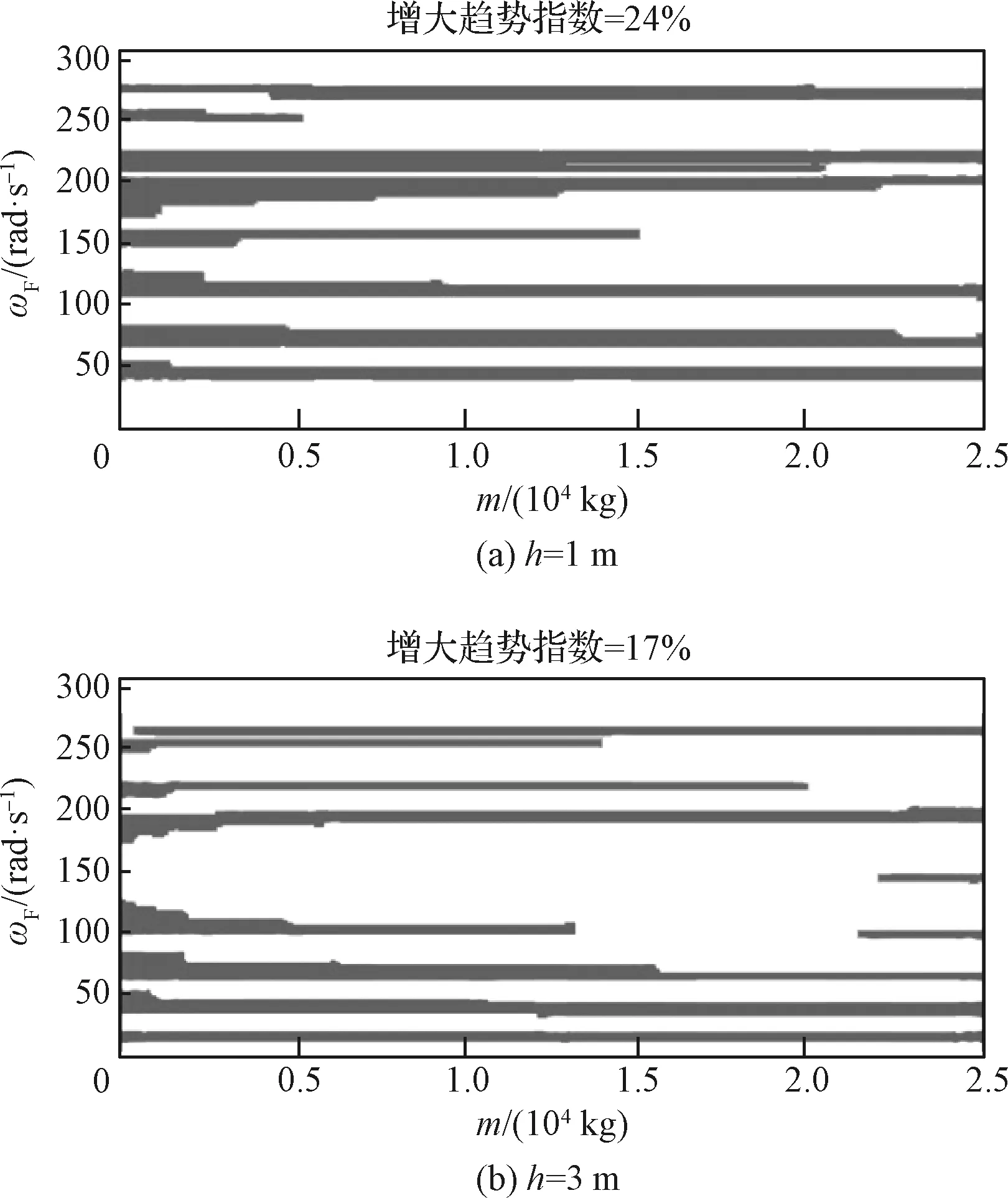
对比相同质心高度、不同基频的分布图,白色及灰色区域占比变化很小,说明基频对横向质心等效加速度随航天器质量的变化趋势影响并不明显。
1.3.2航天器质心高度对质心等效加速度的影响
采用同样方法,在给定的航天器基频以及质量组合下分析质心高度对横向质心等效加速度的影响,基频分别为30 rad/s, 90 rad/s及150 rad/s,对应质量分别为5000 kg, 15000 kg, 25000 kg。
绘制横向质心等效加速度变化趋势指数随外激励频率以及航天器质心高度变化分布图,如图5~图7所示。可以看出,不同航天器质量以及基频组合下,横向质心等效加速度随质心高度的变化规律并不一致,总体呈现出随着航天器质量增加,横向质心等效加速度随质心高度变化减小趋势占比增加,且不同的基频下,该变化趋势差别较大。ω=30 rad/s及ω=90 rad/s时,不同质量分布图中,白色灰色区域占比变化相对较小;ω=150 rad/s时,随着质量增加,白色区域占比增加十分明显,即横向质心等效加速度随质心高度增加而减小趋势显著增强。
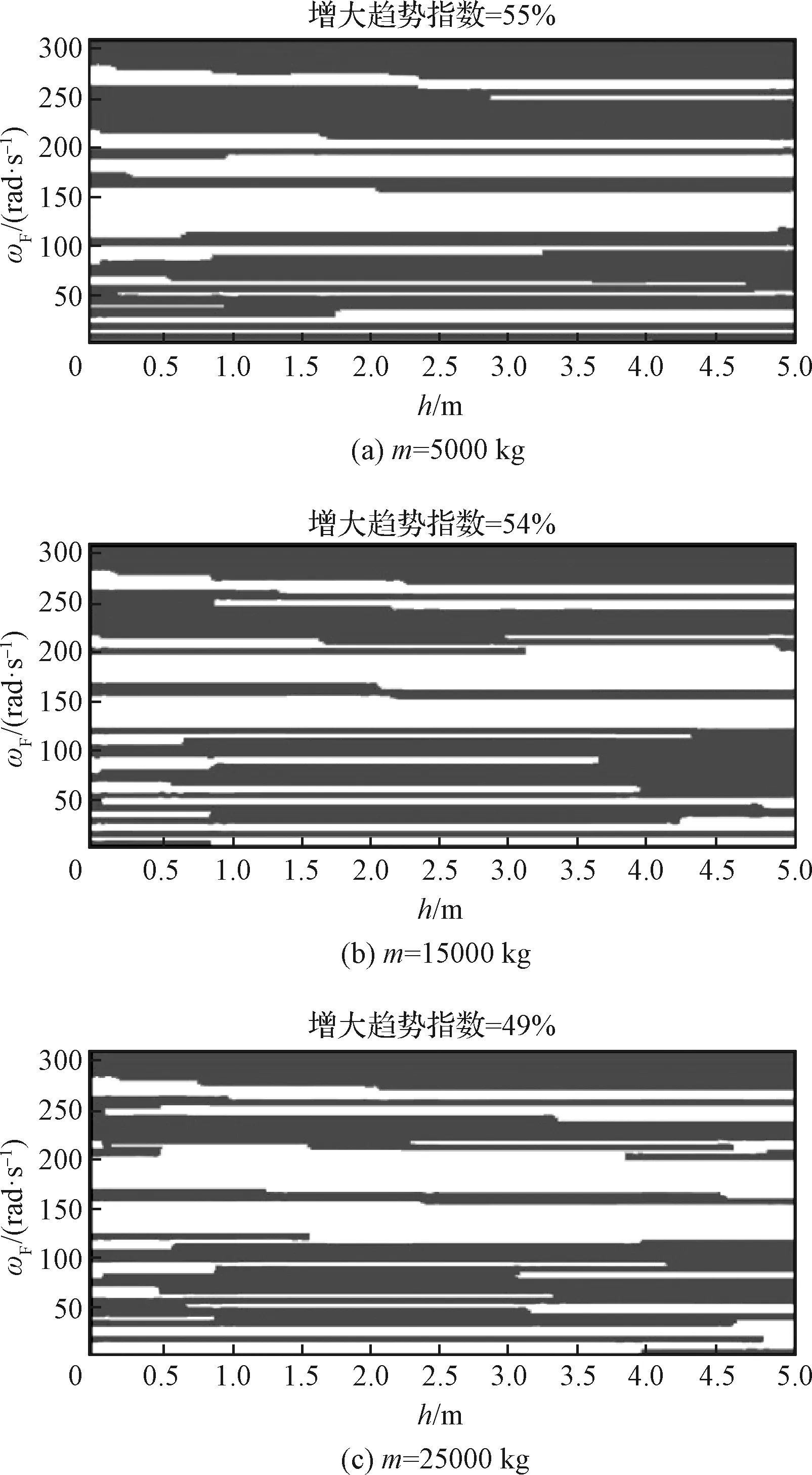
图5 趋势指数随外激励频率及质心高度分布(ω=30 rad/s)Fig.5 Distribution of trend index on frequency of external excitation and centroid location (ω=30 rad/s)
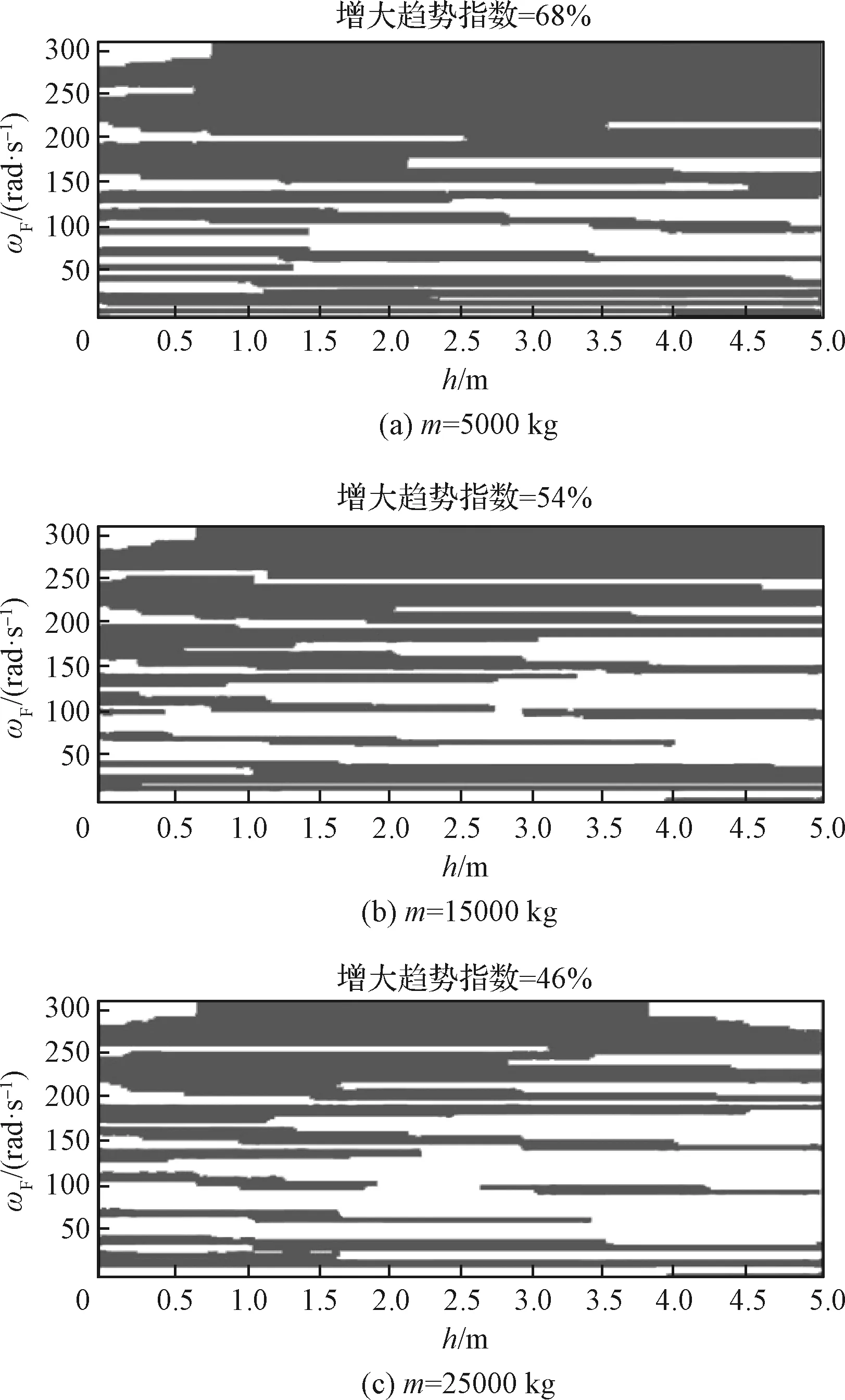
图6 趋势指数随外激励频率及质心高度分布(ω=90 rad/s)Fig.6 Distribution of trend index on frequency of external excitation and centroid location (ω=90 rad/s)
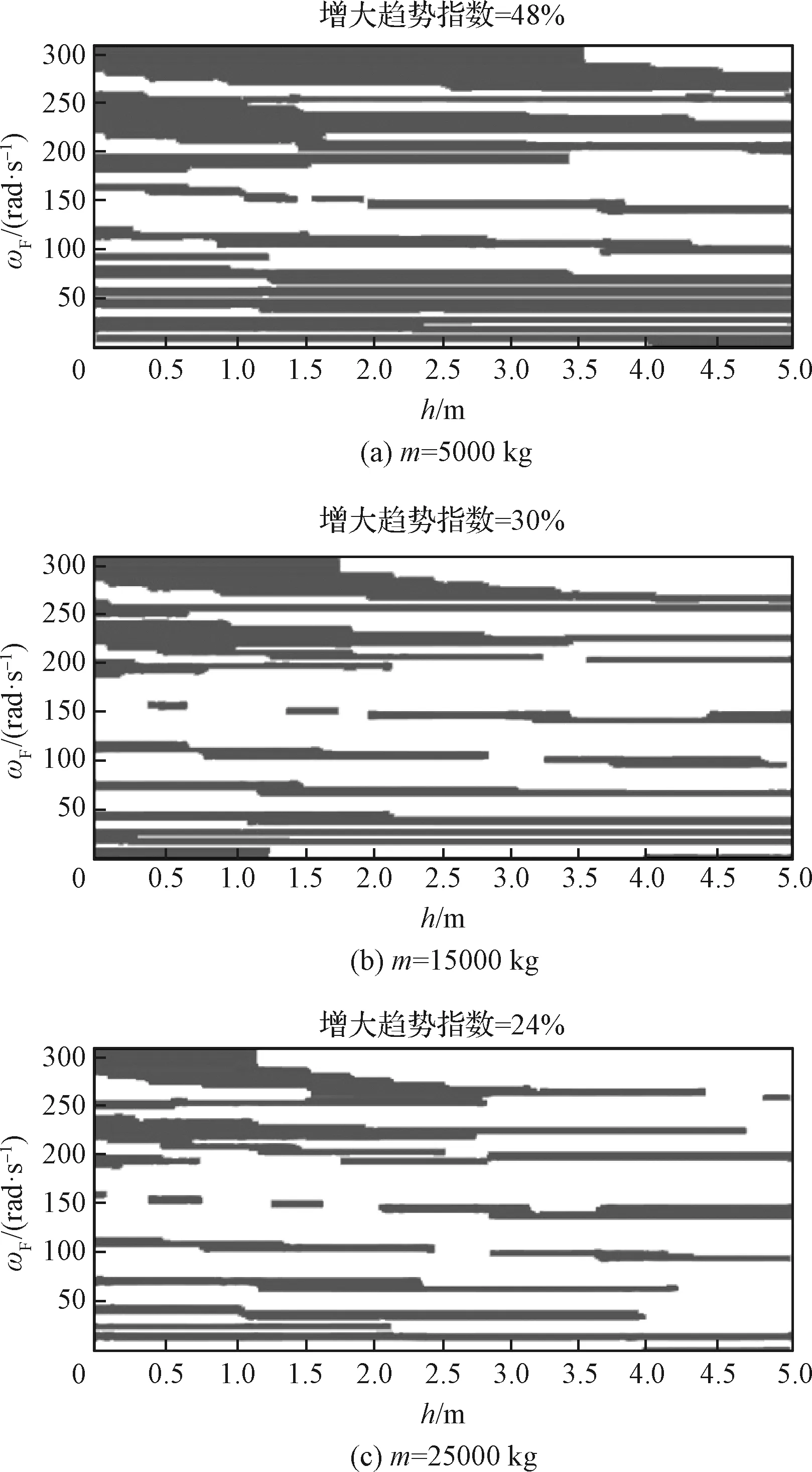
图7 趋势指数随外激励频率及质心高度分布(ω=150 rad/s)Fig.7 Distribution of trend index on frequency of external excitation and centroid location (ω=150 rad/s)
1.3.3航天器基频对质心等效加速度的影响
采用同样方法,在给定的航天器质量及质心高度组合参数下分析基频对横向质心等效加速度的影响,质心高度分别为1 m,3 m,5 m,对应质量分别为5000 kg,15000 kg,25000 kg。
绘制横向质心等效加速度变化趋势指数随外激励频率和基频的分布图,如图8~图10所示。从横向质心等效加速度随基频的变化趋势中可以看出,不同质量及质心高度的航天器,其分布图中白色灰色区域占比没有明显变化规律,可认为单个基频参数对横向质心等效加速度的影响较小,两者相关性较弱。
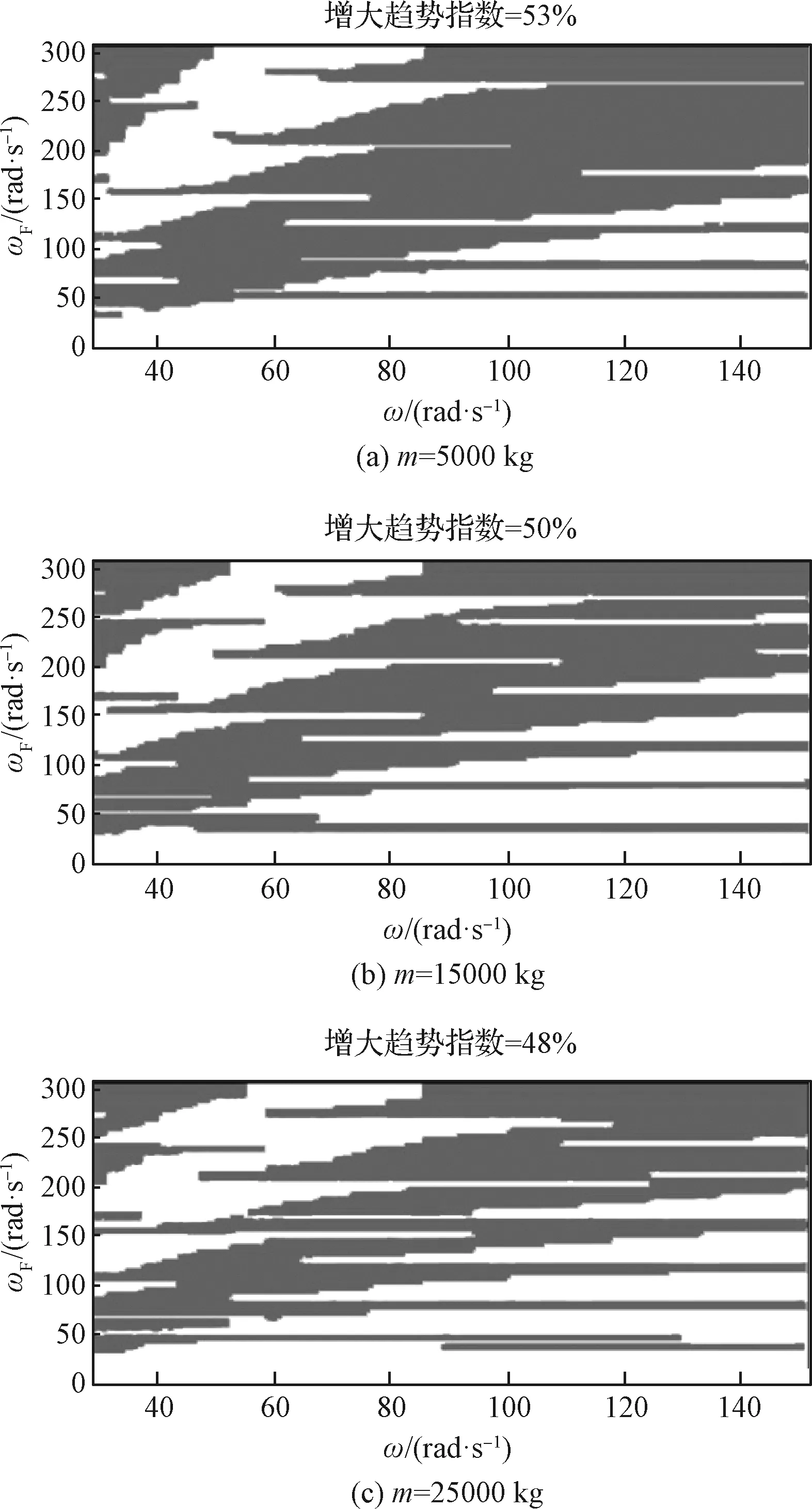
图8 趋势指数随外激励频率及基频分布(h=1 m)Fig.8 Distribution of trend index on frequency of external excitation and fundamental frequency of spacecraft (h=1 m)

图9 趋势指数随外激励频率及基频分布(h=3 m)Fig.9 Distribution of trend index on frequency of external excitation and fundamental frequency of spacecraft (h=3 m)
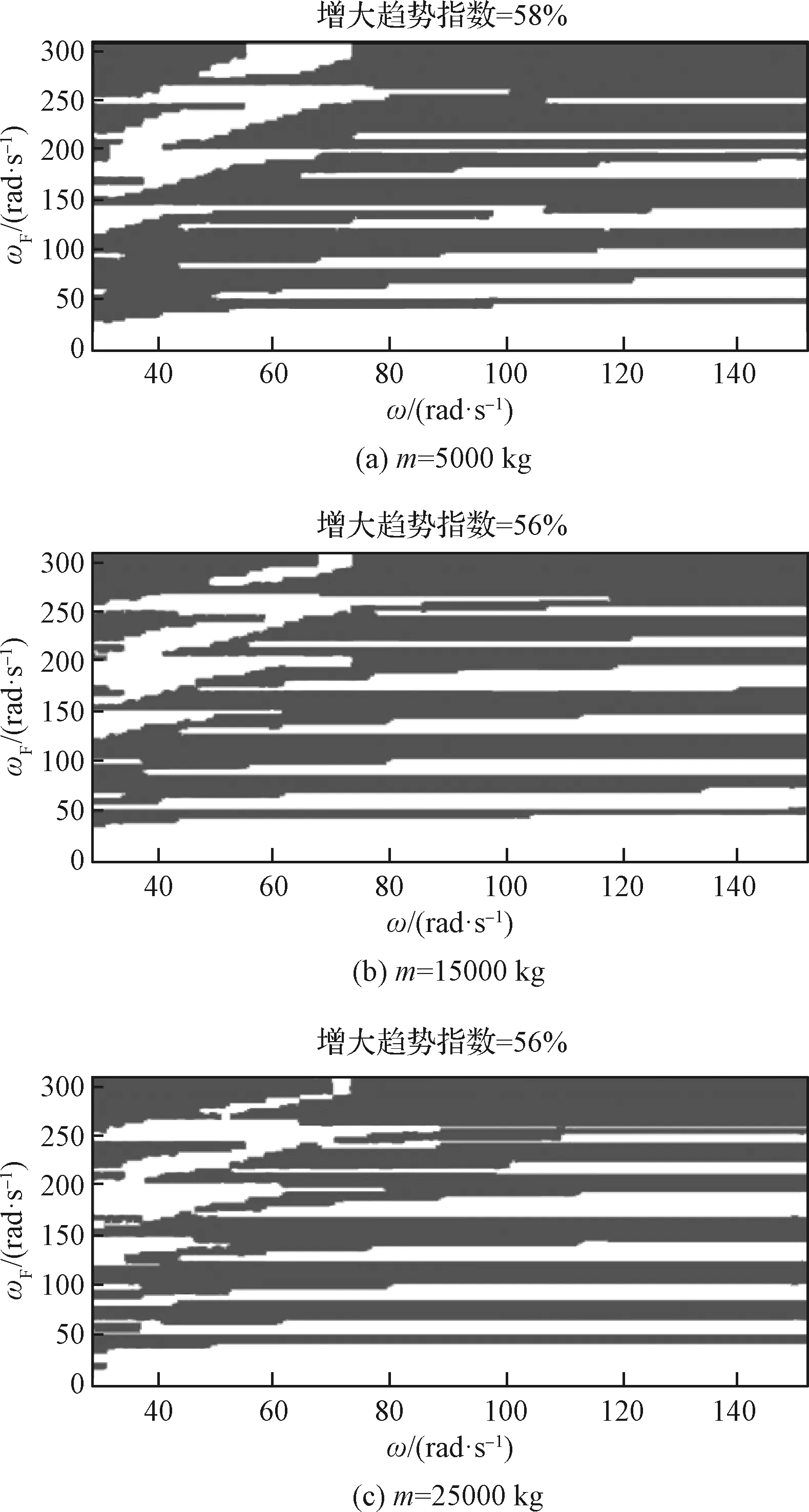
图10 趋势指数随外激励频率及基频分布(h=5 m)Fig.10 Distribution of trend index on frequency of external excitation and fundamental frequency of spacecraft (h=5 m)
2 器箭界面动态内力仿真及精细化设计
前面基于分支梁动力学理论,建立了质心等效加速度的解析表达式,并基于解析表达式对质心等效加速度随主要参数变化趋势进行了研究,阐明了质心等效加速度与不同参数之间的相关性。
考虑理论解析时对器箭组合体和激励形式进行了简化,理论解仅用于分析横向质心等效加速度随不同参数的变化趋势,无法得到较为准确的横向质心等效加速度分布用于器箭精细化设计,因此本章以某型火箭为例,建立器箭动力学有限元模型。通过设计不同航天器的质量、质心位置以及基频等特性参数组,耦合打靶仿真分析得到跨声速飞行工况下真实的质心等效加速度分布,并结合理论分析的规律,对质心等效加速度数据开展分类统计分析。基于统计分析结果,完成器箭界面质心等效加速度条件的精细化设计。
2.1 横向质心等效加速度分布分析
根据航天器合理参数范围,确定参数区间见表2,在给定区间内随机生成航天器质量、质心高度以及基频参数组合,并建立航天器有限元模型,其与火箭有限元模型组合后开展器箭动力学耦合分析,通过打靶仿真得到各参数组合下的质心等效加速度。

表2 航天器参数范围Table 2 Range of spacecraft parameters
根据理论分析规律,横向质心等效加速度与航天器质量有明显的相关性,同时质心高度会对变化趋势产生一定影响,航天器基频对质心等效加速度的影响具有较大的不确定性,因此可按照质心高度对仿真结果进行划分,在每个区间内对质心等效加速度随航天器质量的变化规律进行分析,获得不同质心高度航天器对应的横向质心等效加速度随有效载荷质量的分布曲线如图11所示。
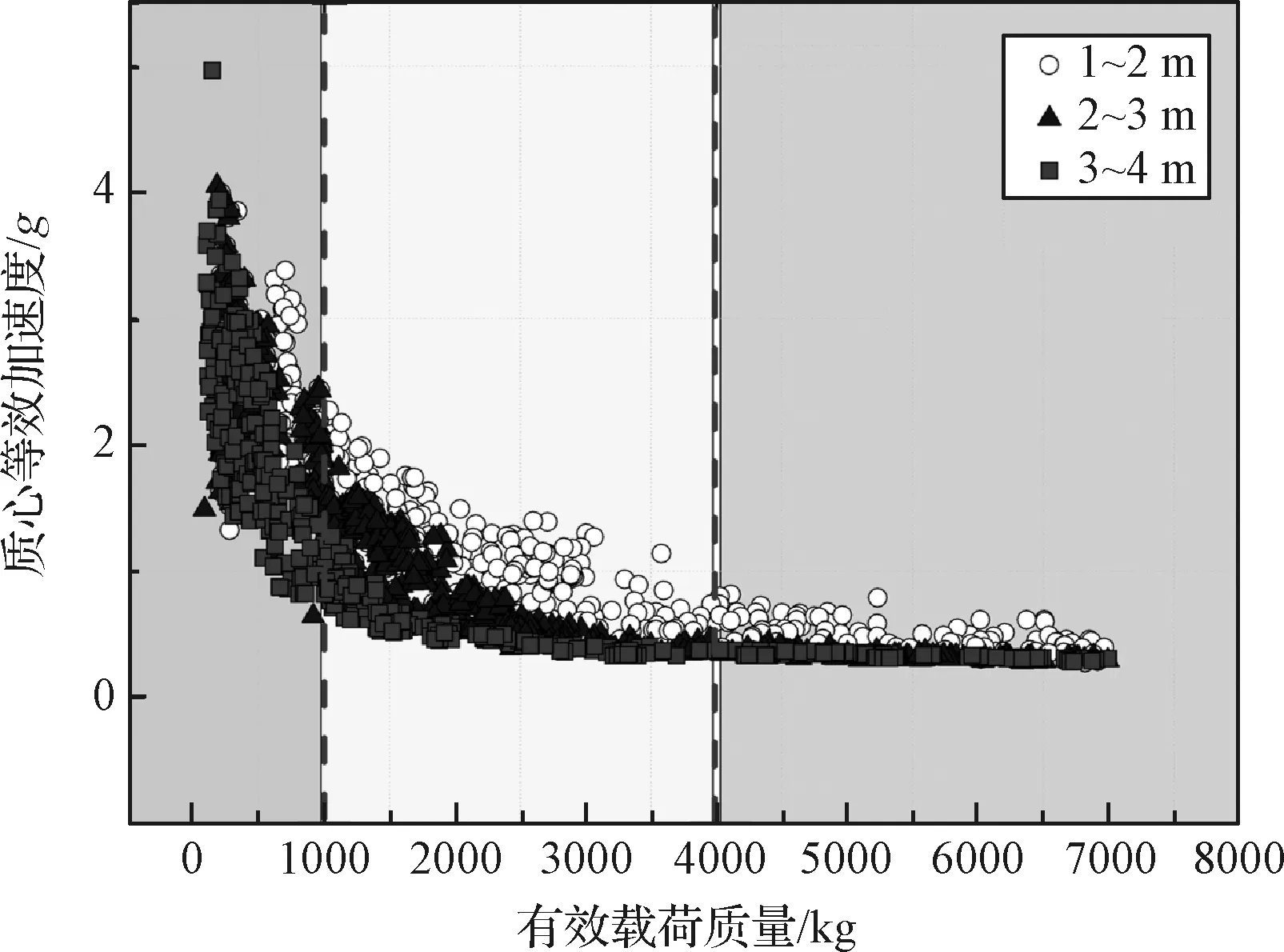
图11 不同质心高度航天器质心等效加速度随质量分布Fig.11 Distribution of equivalence acceleration of spacecraft with different centroid locations
根据上述分布规律,可以再按照航天器质量将不同高度区间的横向质心等效加速度的变化曲线划分为三个区间,其中,当航天器质量<1000 kg时,横向质心等效加速度随着航天器质量的增加迅速降低;而当航天器质量1000 kg≤m<4000 kg时,随着航天器质量的增加,横向质心加速度也会有明显的降低,但是其下降速率要明显低于m<1000 kg时;当航天器质量m≥4000 kg时,横向质心等效加速度随质量的下降曲线较平缓,该区间航天器质量已不是影响横向质心等效加速度的主要因素,质心高度对横向质心等效加速度的影响增强。
2.2 器箭界面动态内力精细化设计
根据上节的分析结论,针对任意火箭构型,可开展器箭界面动态内力的精细化设计。仍以上节中的火箭为对象,对器箭界面动态内力精细化设计过程进行说明。
首先,按照质心高度区间,对横向质心等效加速度精细化设计,选取1.0 m≤h<2.0 m,2.0 m≤h<3.0 m以及3.0 m≤h<4.0 m三个区间进行分类统计,在各区间内绘制横向质心等效加速度关于航天器质量的分布图,如图12~图14所示。
然后,在不同质心高度类别再按照质量区间进行分档,可按照各区间打靶仿真得到的横向质心等效加速度最大值(当区间子样较多时取99%概率统计值),考虑动力学分析不确定性系数(一般取1.25),分别确定各区间的横向质心等效加速度设计值。图12~图14中阴影柱状分布即为不同质量范围的横向质心加速度设计值(工程应用需确保子样数足够),而该型火箭跨声速工况原设计值为1.5g。可以看出,当卫星质量m≥2000 kg时,且质心高度h≥3.0 m时,设计值减小至约0.7g,优化效果达到50%以上。
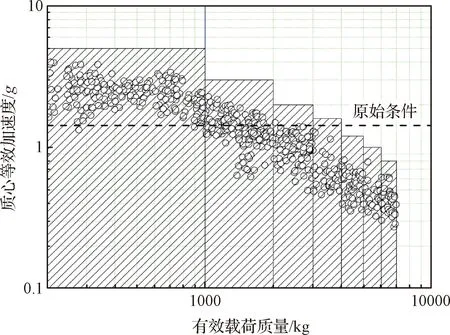
图12 质心等效加速度分布及精细化设计(1.0 m≤h<2.0 m)Fig.12 Distribution and fine design of equivalence acceleration of spacecraft (1.0 m≤h<2.0 m)
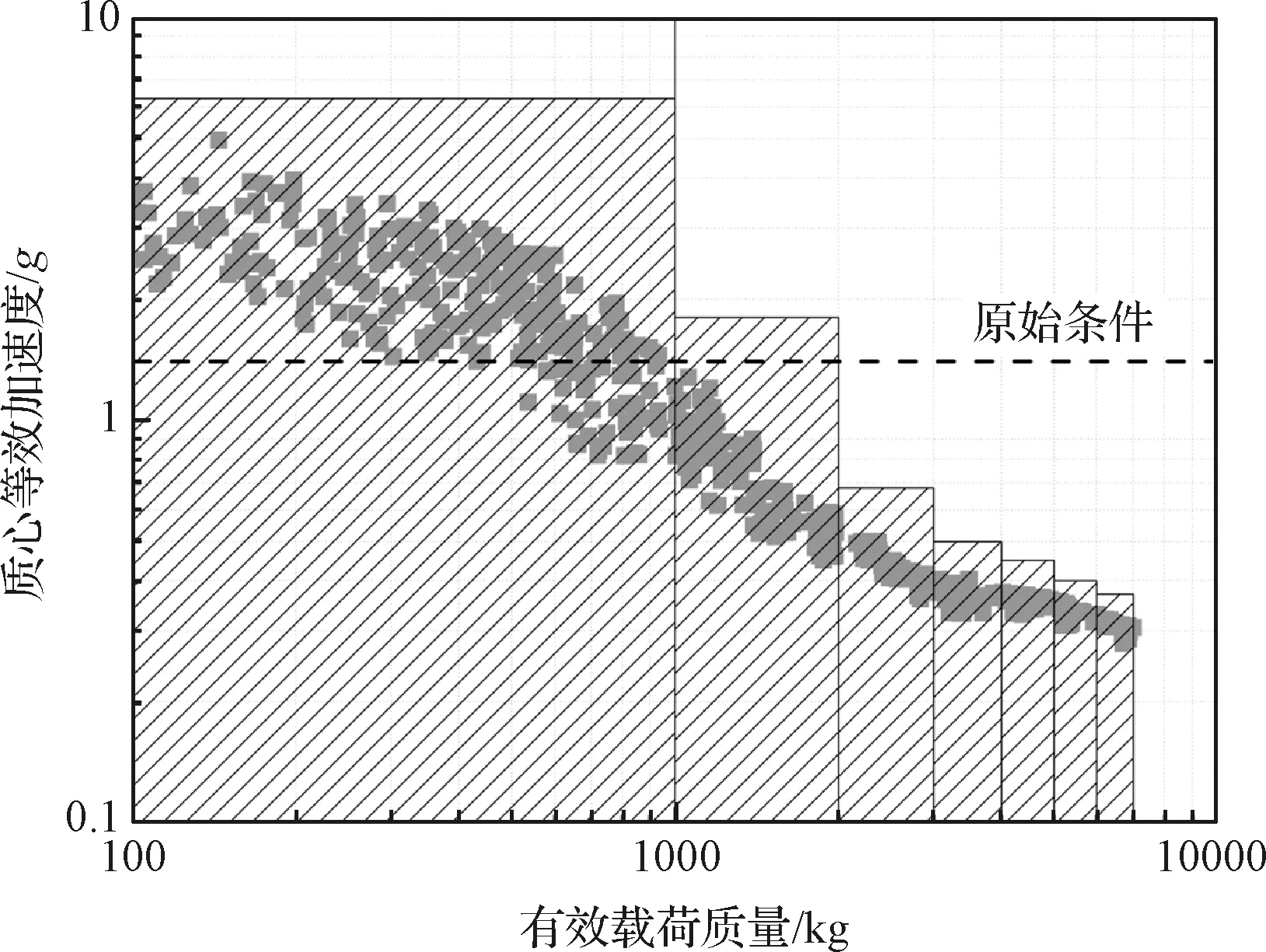
图14 质心等效加速度分布及精细化设计(3.0 m≤h<4.0 m)Fig.14 Distribution and fine design of equivalence acceleration of spacecraft (3.0 m≤h<4.0 m)
当然,为了确保精细化设计条件的正确性,通常在航天器和火箭设计完成后,需根据真实状态再次开展动力学耦合分析,验证精细化设计条件的覆盖性,避免出现复杂因素导致的小概率不确定性。
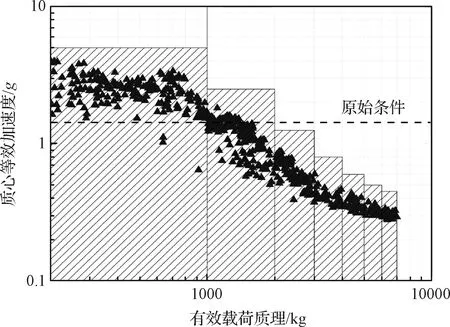
图13 质心等效加速度分布及精细化设计(2.0 m≤h<3.0 m)Fig.13 Distribution and fine design of equivalence acceleration of spacecraft (2.0 m≤h<3.0 m)
3 结 论
本文基于分支梁动力学理论,推导了跨声速飞行时器箭界面动态内力(横向质心等效加速度形式)的解析表达式,辨识出外激励频率、航天器质量、质心高度、基频等主要影响参数,并对横向质心等效加速度随航天器质量、质心高度、基频的变化趋势开展了系统研究。结合理论研究规律,采用器箭动力学耦合仿真方法,通过随机生成航天器质量、质心高度、基频,得到了不同质心高度、质量下横向质心等效加速度的分布规律,并基于加速度分布的统计分析结果,制定了一种器箭界面动态内力的精细化设计方法,研究主要得到以下结论:
1) 根据理论解析推导,横向质心等效加速度与外激励频率、航天器质量、质心高度、基频等参数均存在联系。
2) 横向质心等效加速度与航天器质量间有明显的相关性,随着航天器质量增加有明显的下降趋势;质心高度对横向质心等效加速度的影响规律在不同条件下存在较大差异,但整体上随着质量增加,横向质心等效加速度随着质心高度增加而下降的趋势增强,而基频对横向质心等效加速度的影响并不明显。
3) 针对任意火箭,可通过开展器箭耦合分析打靶仿真,并按照质心高度及质量区间进行分类统计,对器箭界面动态内力完成精细化设计。该精细化方法已在长征五号B和长征七号甲等新一代运载火箭上成功应用,显著降低了器箭设计载荷。
本文聚焦刚度分布较均匀的航天器界面载荷设计规律和优化方法研究,对于刚度分布存在较大差异的航天器,还需增加振型等影响参数。此外,未来将结合理论和仿真方法,进一步系统研究外激励及器箭多个参数的耦合作用效应,补充完善器箭载荷设计优化方法。
