基于AOA-LSTM的施工升降机电机轴承剩余寿命预测
2023-04-14王莉静张建业
郗 涛,王 通,王莉静,张建业
(1.天津工业大学 机械工程学院,天津 300387; 2.天津城建大学 控制与机械工程学院,天津 300384)
施工升降机是建筑领域广泛应用的工程机械,其中,电机主轴轴承作为施工升降机的关键零部件,一旦失效将会导致升降机及整个建筑作业的停工。失效的主要由轴承的故障及运行过程中的寿命退化引起,为在轴承达到失效点前判断其健康状况,对轴承进行退化状态评估和剩余寿命预测具有重要作用[1-3]。
近年来,滚动轴承的剩余寿命预测是机械设备预测和健康管理领域的热点研究话题之一,目前研究领域主要基于数据驱动的方法建立预测模型[4]。徐洲常等[5]通过主成分分析(principal component analysis,PCA)方法把提取的高维退化特征融合成归一化指标,并输入到回归型支持向量机(support vector machine,SVM)预测模型中进行轴承的寿命预测;胡小曼等[6]利用相关向量机(relevance vector machine,RVM)建立预测模型进行滚动轴承剩余寿命预测,取得较好的预测结果。随着深度学习的发展,神经网络预测模型被广泛应用于轴承寿命预测。王奉涛等[7]提出长短时记忆网络的寿命预测方法;尹诗等[8]利用双向循环神经网络(bidirectional recurrent neural network,BI-RNN)的方法预测风电机组主轴承的剩余寿命;韩林洁等[9]提出双向长短时记忆网络(bi-directional long short term memory,BILSTM)的滚动轴承剩余寿命预测方法。上述研究虽然在设备寿命预测方面取得了较好的成果,但在工程机械领域的应用较少,同时预测模型的关键参数由经验值确定,准确率较低。
因此,本文提出一种基于算术优化算法和长短时记忆网络(arithmetic optimization algorithm and long short term memory,AOA-LSTM)的施工升降机电机轴承剩余寿命预测方法。首先,对原始振动信号提取时域和频域特征指标;其次,利用随机森林算法,对提取的高维特征指标进行重要度分析,选择重要度高的特征指标构建退化特征决策表;最后,利用算术优化算法(arithmetic optimization algorithm, AOA)长短时记忆网络(long short term memory,LSTM)模型中的网络层数、每层网络神经元个数和学习率,选择最优参数建立预测模型,并采用均方根误差(root mean square,RMSE)和平均绝对误差(mean absolute error,MAE)指标评估预测模型。该方法分别利用西安交通大学(Xi’an Jiaotong University and the Changxing Sumyoung Technology,XJTU-SY)验证数据集和某施工升降机电机轴承的采集数据,并取得较好的预测结果,证明该方法的可行性和鲁棒性。
1 理论基础
1.1 算术优化算法
AOA 是Abualigah 等[10]在2021 提出的元启发式新型智能优化算法,具有良好的收敛速度和求解精度,核心原理是利用基本的算术运算实现算法的寻优过程,其中乘除运算更新全局最优位置,避免产生局部解;加减运算更新局部最优位置,提高求解精度。算术优化算法优化过程分初始化阶段、探索阶段和开发阶段3 个阶段。其中,探索阶段包括除法运算(D)与乘法运算(M),开发阶段包括加法运算(A)和减法运算(S)。
1.1.1 初始化阶段
初始化参数,在参数范围内随机设置初始解X,每次迭代的最佳候选解确定为当前最优解,X为
式中:X为N×n维矩阵
在算法迭代开始前通过数学优化器加速函数(MOA)对探索阶段或者开发阶段进行选择,取随机数r1∈[0,1]与MOA 进行比较,r1≥fMOA选择探索阶段迭代寻优,反之选择开发阶段,MOA定义式为
式中:fMOA(t)为第t次迭代的函数值;t为当前迭代次数;Mt为最大迭代次数;fmax为fMOA的最大函数值;fmin为fMOA的最小函数值。
1.1.2 探索阶段
在探索阶段主要利用除法机制和乘法机制两个搜索机制作为搜索策略,随机数r2∈[0,1]与0.5进行对比,若r2>0.5 选择最外层除法策略,反之选择乘法策略。式(3)为位置更新函数,式(4)为探索阶段迭代过程:
式中:fMOP(t)为t次迭代时的函数值;a为敏感参数。
式中:xi(t+1)为下一次迭代的第i个解;xi,j(t+1)为第i个解在当前迭代的第j个位置;fbest(xj)为当前迭代最优解的第j个位置;UBj和LBj为第j个位置的上界和下界;ε为一整数;m为调节搜索过程的控制参数。
1.1.3 开发阶段
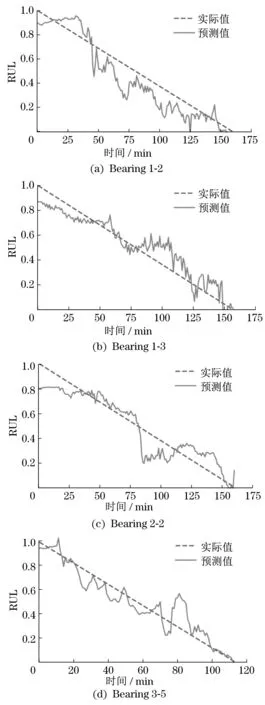
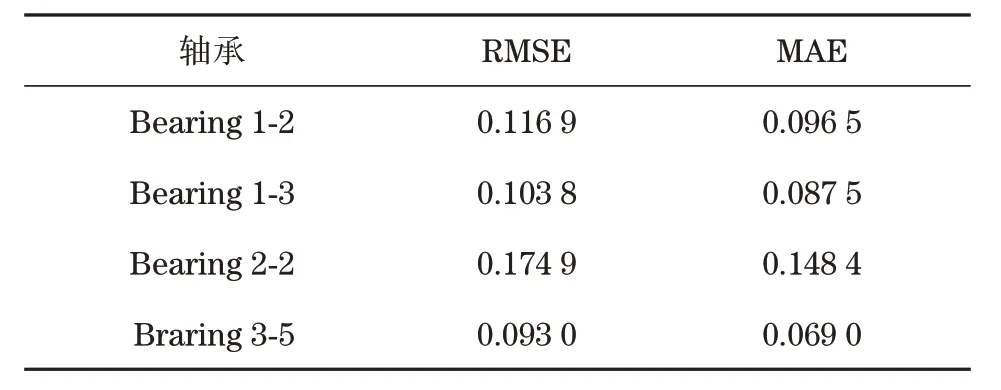
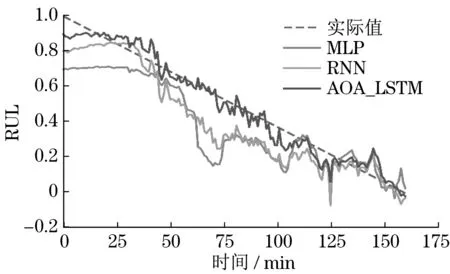
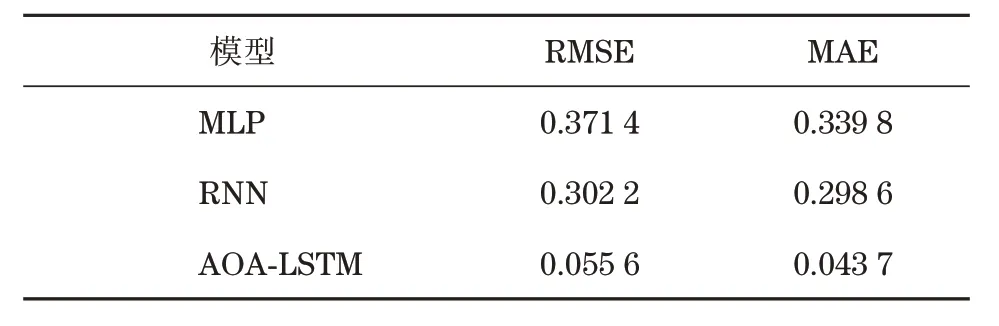
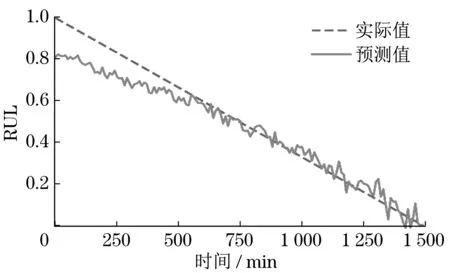
开发阶段利用加法机制和减法机制作为搜索策略进行局部寻优,此阶段搜索范围小,准确度较高。当随机数r1 式中:μ为调节搜索过程的控制参数。 循环神经网络(recurrent neural network,RNN)适合处理时序数据,但在模型训练过程中存在梯度消失、梯度爆炸等问题,LSTM[11]利用门控机制原理使模型具有更强的记忆能力,能够处理更长的时序数据,同时解决了RNN 存在的梯度问题。LSTM 的3 个门控机制分别为遗忘门、输入门和输出门,门控机制通过激活函数把输入数据压缩到[0,1]区间内,同时控制数据的流动。 LSTM 模型结构如图1 所示,箭头方向为数据流动方向,ct-1、ct分别为上一个时间戳输入的记忆数据和当前时间戳输出的记忆数据,ht-1、ht分别为上一个时间戳的输入数据和当前时间戳的输出数据,xt为当前时间戳的输入数据。 图1 LSTM模型结构Fig.1 LSTM model structure 遗忘门为上一个时间戳的输入ct-1和当前时间戳的遗忘门控制变量gf的乘积,输出为gfct-1: 式中:Wf、bf为遗忘门的权重参数和偏置参数;xt为当前时间戳的输入参数;ht-1为上一时间戳的输出数据;σ为激活函数。 输入门为输入门控值变量gi和当前输入数据经过tanh激活函数变换后的状态向量乘积,输出数据为͂: 式中:Wc为输入门的权重参数;bc为偏置参数;tanh为激活函数。 式中:Wi为输入门的权重参数;bi为偏置参数。 输出门为输出门控值变量go和当前时间戳的输出状态向量的乘积,输出数据为ht: 式中:Wo为输出门的权重参数;bo为偏置参数。 LSTM 模型训练过程中参数的选择对网络训练结果影响较大,大部分研究通过经验选择LSTM网络参数,但存在较大误差。本文通过AOA 算法优化LSTM 中的超参数,并利用优化结果建立LSTM 预测模型,关键参数有学习率、网络层数和每层网络的神经元个数。因此,利用AOA 对以上参数寻找全局最优值,并选择RMSE 作为适应度函数: 式中:p为预测值;y为真实值;n为预测样本点个数。 算法优化步骤为: (1) 初始化AOA 算法参数,设置最大迭代次数,随机选择优化参数等,设置均方根误差为适应度函数。 (2) 初始化LSTM 算法参数,设置批处理量等参数,通过初始化优化参数进行模型预测,得到当前迭代适应度值。 (3) AOA 不断迭代更新参数位置,记录每次最优结果,返回步骤2。 (4) 通过步骤2 和3 不断迭代计算最佳适应度值,与记录值对比确定当前最优值是否为最优解,满足迭代条件则终止迭代,输出最优结果,否则返回步骤2 和3 继续更新位置,直到满足迭代条件终止。 AOA-LSTM 预测模型的构建主要分为3 个阶段,即对原始振动信号提取特征并构建退化特征、AOA 优化LSTM 中的超参数、LSTM 预测模型的建立与评估。AOA-LSTM 预测模型流程如图2所示。 图2 AOA-LSTM预测模型流程Fig.2 AOA-LSTM prediction model flow chart 退化特征的构建需要对原始数据提取时域和频域特征指标。时域退化特征提取平均值、标准差、偏度、峭度、最大值、最小值、峰峰值、均方根值、波形因子和裕度因子;频域退化特征提取重心频率、均方频率、频率方差、能量等14 维退化特征,特征提取详细公式参考文献[3]。提取的高维特征指标利用随机森林算法进行特征重要度分析,选择与轴承实际退化特征相关性更高的特征构建退化特征决策表,输入LSTM 预测模型中进行预测与分析。 LSTM 预测模型构建中,退化特征决策表作为训练集输入数据,对应的寿命标签作为训练集标签,为消除不同量纲的影响,对退化特征进行归一化处理,剩余寿命标签初始为1,随着轴承退化过程的进行,剩余寿命最终为0。模型训练结束后输入测试集数据,通过RMSE和MAE评估模型。 平均绝对误差为 式中:p为预测值;y为真实值;n为样本点个数。 选择XJTU-SY 数据集[12]验证该方法的可行性,该数据集包括3种工况下共15组滚动轴承的全生命周期数据,轴承数据集长度和故障类型等信息见表1。实验中选择的轴承型号为LSD UER204滚动轴承,采样频率为25.6 kHz,采样间隔为1 min,采样时间为1.28 s,即每次采样样本点为32 768。实验中轴承施加载荷方向为水平方向,水平方向的加速度振动信号包含更多的有效退化信息,选择该方向的数据进行实验分析。Bearing 1-1 的全寿命轴承数据的时域如图3 所示,由图3 中可知轴承的全生命周期退化过程。 表1 退化特征相对重要性量化结果Tab.1 Quantitative results of relative importance of degradation characteristics 选择Bearing 1-1 提取时域、频域共14 维特征指标,再通过随机森林算法对提取的特征指标进行重要度分析[13],其结果如图4 所示。退化特征重要性量化结果见表1。选择重要度值大于0.04的特征指标共5 维特征构建退化特征决策表,作为LSTM模型的输入数据。 图4 退化特征相对重要性Fig.4 Relative importance of degradation characteristics AOA 对LSTM 中的网络层数、每层网络神经元个数、学习率作为超参数进行优化,选择均方根值作为适应度函数,设置AOA 参数进行模型超参数优化,优化结果为网络层数为2,第1 层神经元个数为88,第2层为35,学习率为0.007 3。 通过AOA 优化结果构建LSTM 预测模型,LSTM网络模型参数见表2。 表2 LSTM网络模型参数Tab.2 LSTM network model parameter 模型训练过程中,MES 损失曲线变化过程如图5 所示,设置迭代次数1 000 次。由图5 可知,训练损失曲线和验证损失曲线随着迭代次数的增加趋于稳定。 图5 损失曲线变化过程Fig.5 The loss curve change process 以Bearing1-1 作为训练集,选择其余4 种轴承作为测试集,不同工况下轴承预测结果如图6 所示,纵轴为剩余使用寿命(remaining useful life,RUL)。由图6 可知,预测值在一定范围内随着实际值上下波动,预测结果较好。 图6 AOA-LSTM预测结果Fig.6 AOA-LSTM prediction results 利用RMSE 和MAE 评估预测模型,评估结果见表3。 表3 预测模型评估结果Tab.3 Prediction model evaluation results 为验证文中所提方法的有效性,选择MLP、RNN 算法与AOA-LSTM 算法对比。3 种不同算法的预测结果对比如图7 所示。由图可知,本文所提方法与实际值预测结果拟合度更高。 图7 不同预测模型预测结果对比Fig.7 Comparison of prediction results of different prediction models 利用RMSE 与MAE 对3 种不同预测模型进行误差评估,结果见表4。由表可知,AOA-LSTM 预测模型误差更小,证明本文所提方法的有效性。 表4 不同预测模型评估结果Tab.4 Evaluation results of different prediction models AOA-LSTM 模型在工程应用中,对某施工升降机的电机轴承采集振动信号数据,该数据包含电机轴承全寿命阶段的共150 组退化数据,每组数据包含2 000 个样本点,采样间隔为10 min。利用本文所提研究方法对采集的振动信号提取特征指标,并提取退化特征后输入AOA-LSTM 预测模型中,预测结果如图8 所示。由图8 可知,在轴承退化阶段和失效阶段,预测结果准确度更高,利用RMSE 和MAE 评估模型,计算结果分别为0.075 8和0.057 4,所提退化特征提取方法和预测模型具有较好的泛化性。 图8 采集数据预测结果Fig.8 Collect data prediction results 本文提出一种基于AOA-LSTM 的施工升降机电机轴承剩余寿命预测方法,通过理论模型与工程实际应用相结合,预测结果较准确,得到以下结论。 (1) 对原始振动信号提取时域和频域特征指标,并利用随机森林算法进行重要度分析,进一步选择的退化特征与实际退化过程相关性更高。 (2) 通过AOA 对LSTM 神经网络寻找最优参数组合,避免经验选择参数的不足,对XJTU-SY 数据集中不同工况的滚动轴承进行预测,预测结果准确度较高。与MLP 和RNN 模型对比,所提方法的预测误差更小。 (3) 分别通过XJTU-SY 数据集和某施工升降机电机轴承的采集数据验证所提方法,XJTU-SY数据集上预测结果:RMSE、MAE 分别为5.56%和4.37%,采集数据RMSE、MAE 分别为7.58% 和5.74%,预测结果具有较高的准确率,证明所提方法的可行性。1.2 LSTM模型及参数优化

1.3 预测模型构建与评估
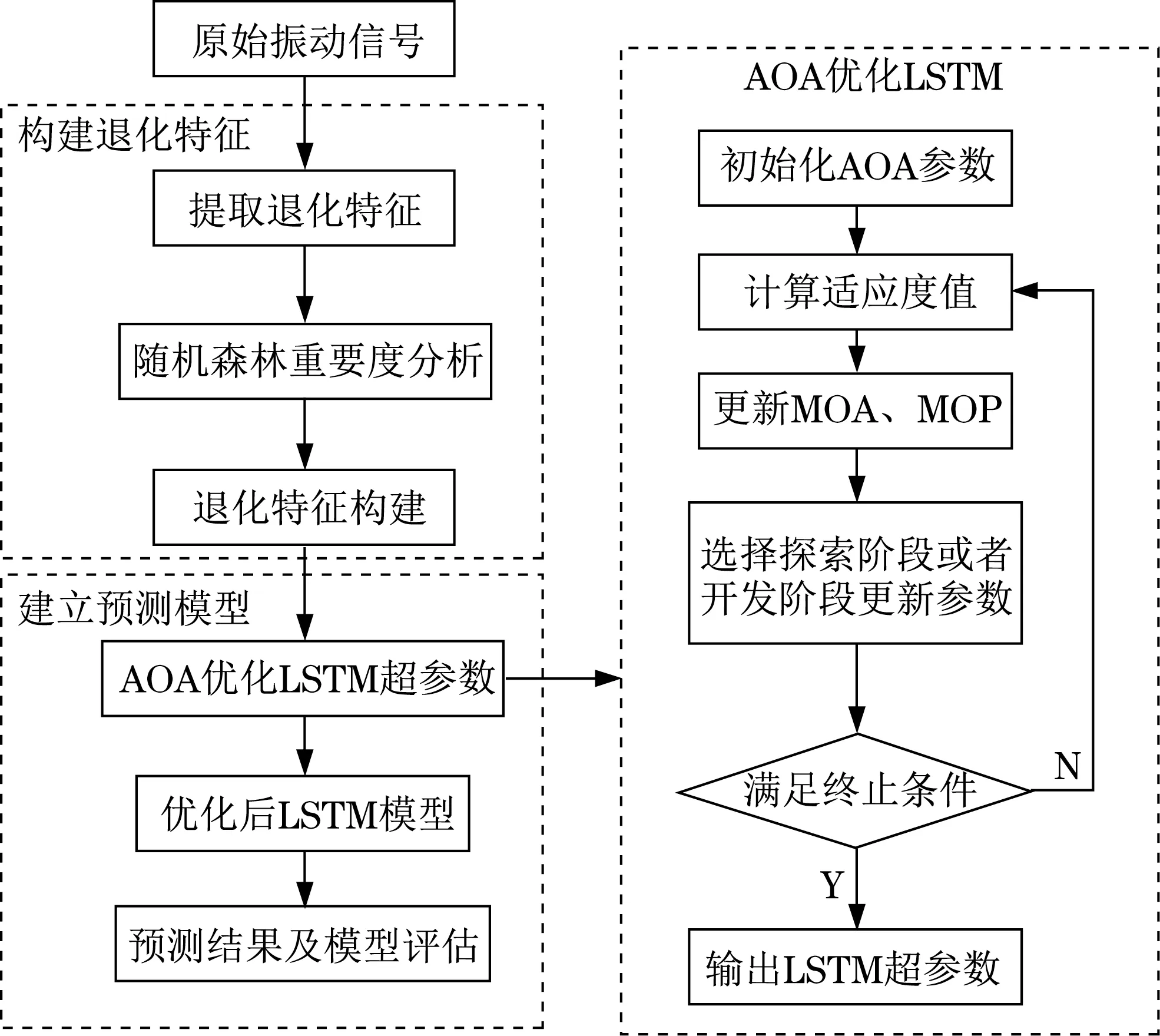
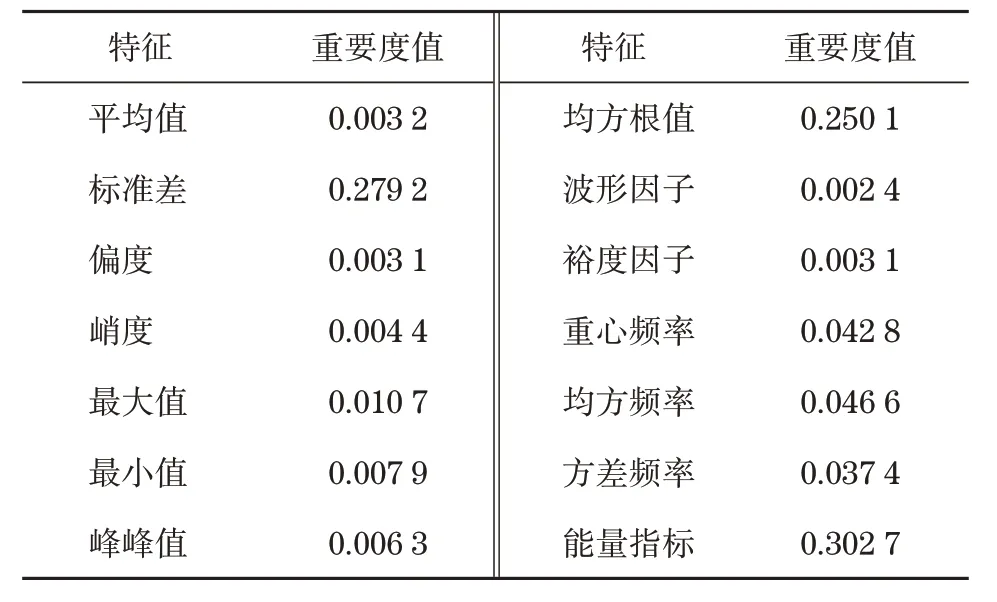
2 实例分析与验证
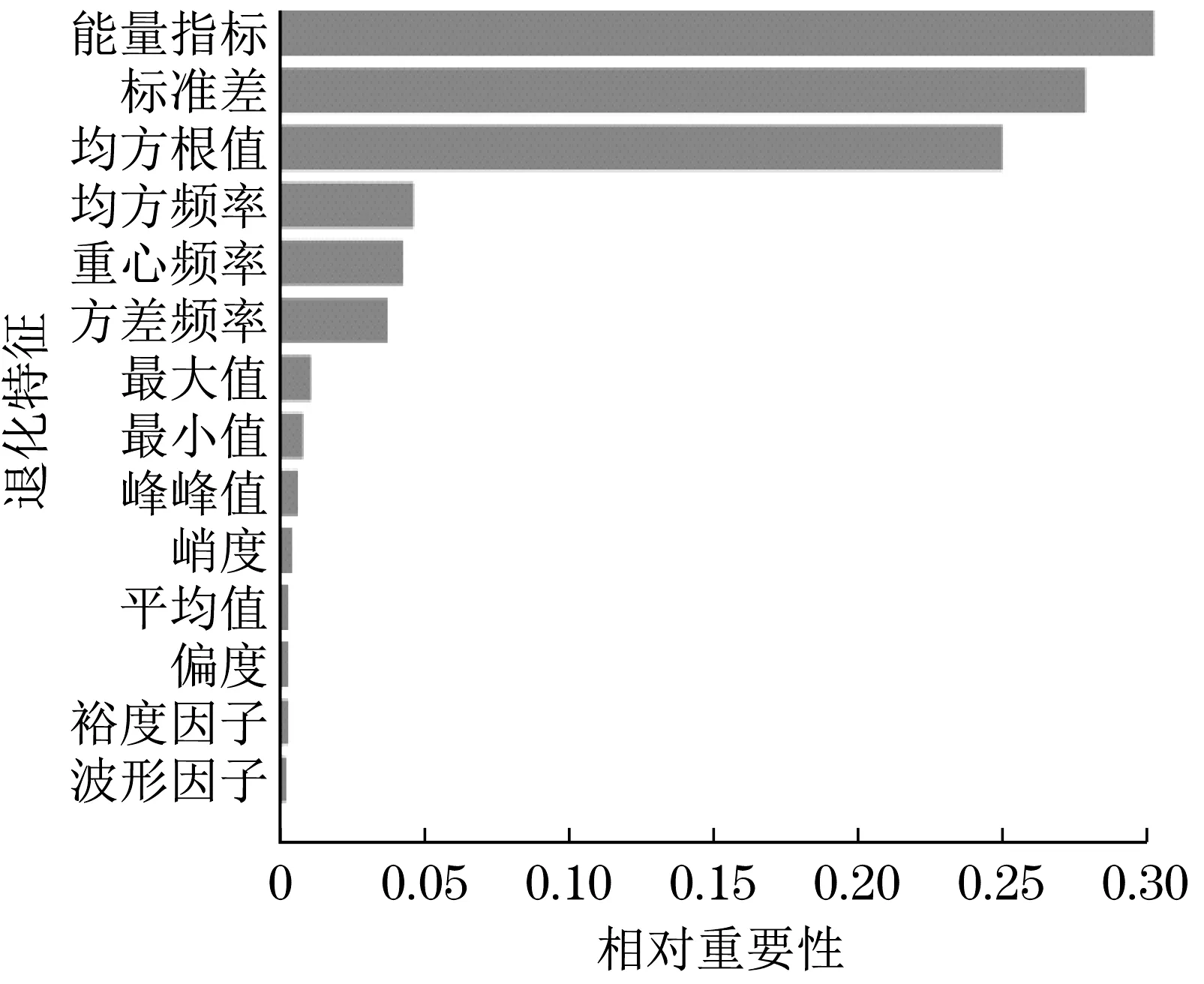

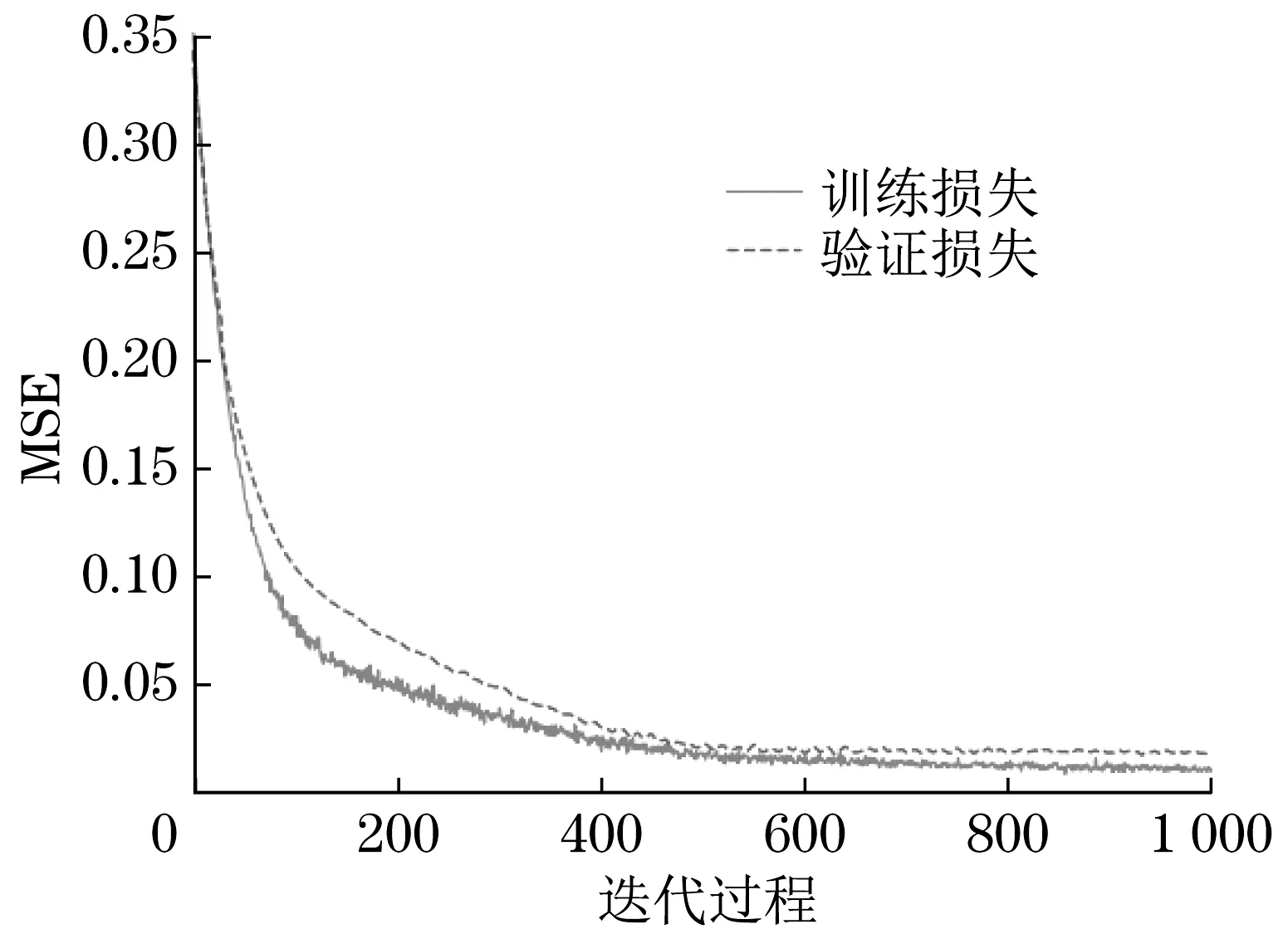
3 结论
