6自由度液压机器人末端执行器控制策略

李亚昆，崔战友

（郑州工业应用技术学院 机电工程学院，河南 郑州 451100）

目前，机器人的驱动主要采用电机、液压和气动系统。液压驱动系统具有反应速度快、运动稳定、强负荷力［1-2］等优点，较快占据了主导地位。但也存在一些不足，比如机器人关节尺寸受到限制，不适合重型场合；液压系统阀控的动态特性不连续，易受到负载的扰动等，使得机器人运动精度下降。与国外发达国家相比，我国在机器人液压驱动系统方面的研究起步较晚，存在一定的差距。如何在短时间内提高机器人液压驱动控制精度，尽快赶超国外液压机器人先进控制技术，使得机器人在复杂环境中保持较高的输出精度，是科研人员研究的热门方向。因此，提升机器人液压驱动控制性能，具有十分重要的意义。

当前，为了提高机器人末端执行器定位精度，国内外学者对机器人末端执行器定位精度展开了研究。Navid等［3-4］研究6自由度并联机器人线性化径向基函数（radial basis function，RBF）神经滑模控制方法，通过仿真验证其跟踪效果，仿真结果满足了设计的要求。朱龙英等［5-6］研究并联机器人神经网络自适应控制方法，将改进的粒子群算法用于神经网络比例积分微分（proportional integral derivative，PID）控制参数调整，从而得到并联机器人最优控制参数。明瑞浩等［7-8］研究2 自由度并联机器人非线性同步控制方法，设计了机器人非线性同步控制方案，通过仿真验证机器人末端执行器跟踪误差，具有较好的跟踪精度。以往研究的并联机器人末端执行器，在控制精度方面有所提高，但随着企业加工精度的要求越来越高，现有控制精度已较难满足高精度产品的需要。因此，本文建立6 自由度液压并联机器人示意图，设计了增量式非线性逆控制方法。在不同期望信号条件下，通过Matlab软件对并联机器人末端执行器位置跟踪误差进行仿真，对比非线性逆控制方法的输出效果，为深入研究6 自由度并联机器人末端执行器跟踪误差提供参考价值。

1 液压系统动力学模型

本文研究的6自由度液压并联机器人如图1所示，主要包括上下2 个平台、6 个伺服液压缸和6 个活塞杆。图1 中，XaYaZa-Oa为上平台坐标系，XbYbZb-Ob为下平台坐标系，1、2、3、4、5、6 为6 个液压缸。下平台为基座，通常固定不动，通过液压缸驱动上平台运动。液压驱动系统如图2 所示，图中，xm为滑阀位移，q为执行器位移矢量。当滑阀向左移动时，液压油通过油管流入气缸室，驱动执行器向右移动；当滑阀向右移动时，液压油通过油管流入气缸室，驱动执行器向左移动。执行器向左或者向右移动，从而驱动6 自由度机器人上平台的伸长与缩短。

n杆机器人的刚体动力学方程一般采用Ⅱ阶非线性微分方程。特别是对于本研究中所考虑的并联机器人系统，采用牛顿-欧拉方法来获得笛卡尔空间中的动力学方程如下：

式中：z、s′和s″分别为笛卡尔空间中定义的末端执行器位姿、速度向量和加速度向量；F为驱动力矢量；M为质量矩阵；η为离心力和科里奥利力矩阵；J为雅可比矩阵。

典型阀门控制的单对称液压执行机构如图2所示。

Φp1、Φp2分别为流入和流出气缸室的液压油流量，Ps、Pt分别为供油和回油压力。

液压缸动力学方程［9-10］为

式中：Ap为活塞面积，m2；Cl为泄漏系数，L/s·Pa；PL=（Pp1-Pp2）为液压缸压力差，Pa；Φm=(Φp1-Φp2)/2 为液压油流量，L/s；Cm为液压油液压刚度，Pa/L；q为执行器位移，m。

液压油液压刚度表达式［11］为

式中：E为液压缸油的体积模量，Pa；V1和V2为气缸室体积，L。

对于具有匹配和对称节流孔的理想临界中心阀，液压油流量表达式为

式中：Cd为流量系数，L/m3；w为孔口宽度，m；xm为滑阀位移，m；Ps为供油压力，Pa。

将最大阀门行程xm，max和零负载压力下的最大流量定义为

由式（3）和式（5）可以得到如下表达式：

式中：GA（PL，xm，q）为一个函数表达式；fA（PL，q，q′）为一个函数表达式；u为控制输入。

2 增量非线性动态逆控制

n阶非线性控制输入系统方程式［12］定义为

式中：f为向量场；d为外部干扰；G为控制效果矩阵；h（x）为一个函数表达式。

x、d、h假设是连续的。假设f（x）和G（x）是x的函数，所有微分都是有界的。

假设h（x）=x，系统的相对度为（1，1，…，1）1×n，输出的Ⅰ阶时间导数为

式中：y=f（x）为一个函数。

对于m=n的全驱动系统，如果G（x）是可逆的，采用传统的非线性动态逆或一般的反馈线性化方法。与非线性动态逆方法不同，为了得到所研究系统的增量形式，在每个采样间隔（用下标0 表示）的开始时刻，应用泰勒级数对［13］式（9）中的系统动力学展开后得到表达式如下：

假设对式（10）等式定义为

式中：O为无穷小的一种表示符号。

则式（10）可转换为

式中：x′0为系统状态导数。

利用x和d的连续性及f（x）和G（x）微分的有界性，将式（11）的极限计算为

式（12）中的系统输入u不假定连续性。在给定的每个采样间隔内，采用式（12）中的非线性动态逆设计增量非线性动态逆控制律，表达式为

式中：v为伪控制输入。

对于每个采样间隔，计算控制增量Δu=G-1（x0）（v-x′0）并递归地添加到u0，即前一个样本的集成或测量控制输入，如图3所示。

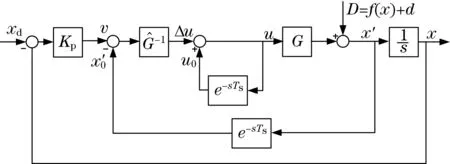
图3 增量非线性动态逆控制器Fig.3 Incremental nonlinear dynamic inversion controller

由于系统被线性化为单积分器，因此，通常选择简单的比例控制器作为伪控制ν。图3 给出了增量非线性动态逆控制器的一般结构，其中表示单个采样时间Ts中的传输延迟。当G存在模型不确定性时，用估计值̑作为控制器。

因此，式（14）写成递归离散形式为

式中：uk、uk+1为控制输入k次和k+1 次；xk-1、x′k-1为控制输入k-1次和k-1次变化率。

由式（12）和式（14）可得表达式如下：

由式（13）和式（16）可知，在无限小的采样时间下，系统是完全线性化的。简单地选择线性控制律v=x′d+Kp（xd-x），则系统误差动力学表达式如下：

式中：e=x-xd为误差；x为实际轨迹；xd为期望轨迹。

3 结果与分析

6自由度液压并联机器人末端执行器采用增量式非线性逆控制方法，通过Matlab软件进行仿真验证，可知执行器跟踪误差效果，并与非线性逆控制输出结果进行对比。仿真参数设置如下：执行器等效质量m= 3 000 kg，液压缸行程l=1.0 m，负载力F= 50 kN，工作压力为P=150 bar，仿真时间t=4 s。

假设并联液压机器人末端执行器期望信号如图4 所示，则采用非线性逆控制方法跟踪误差如图5 所示，采用增量式非线性逆控制方法跟踪误差如图6所示。

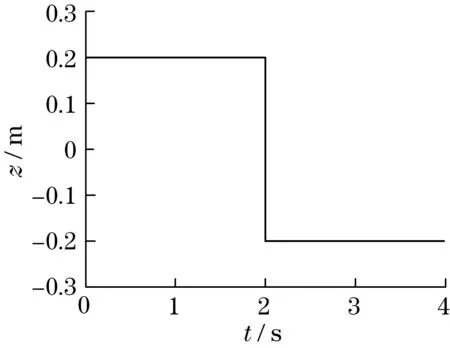
图4 阶跃波信号Fig.4 Step wave signal

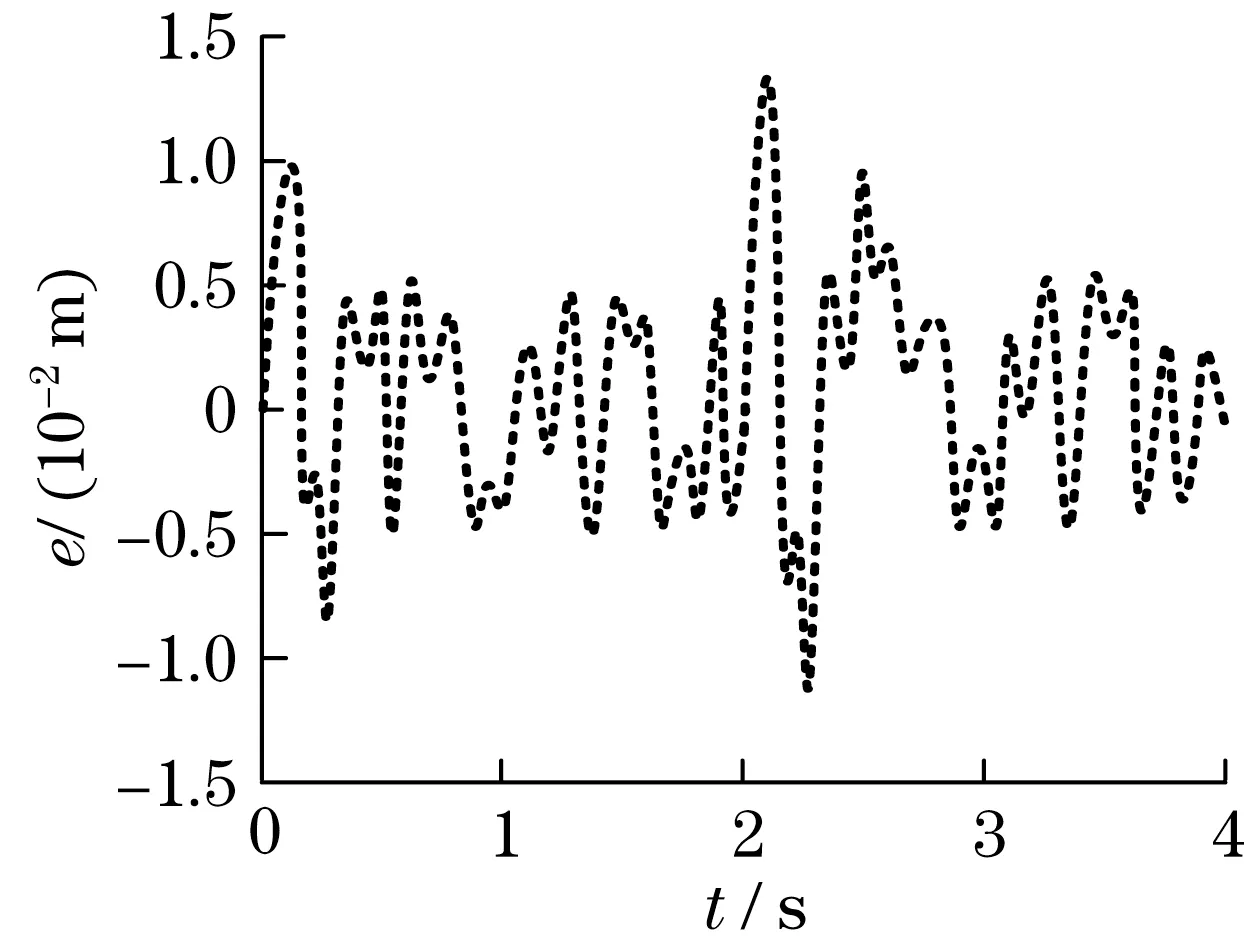
图5 非线性逆控制方法Fig.5 Nonlinear inverse control method

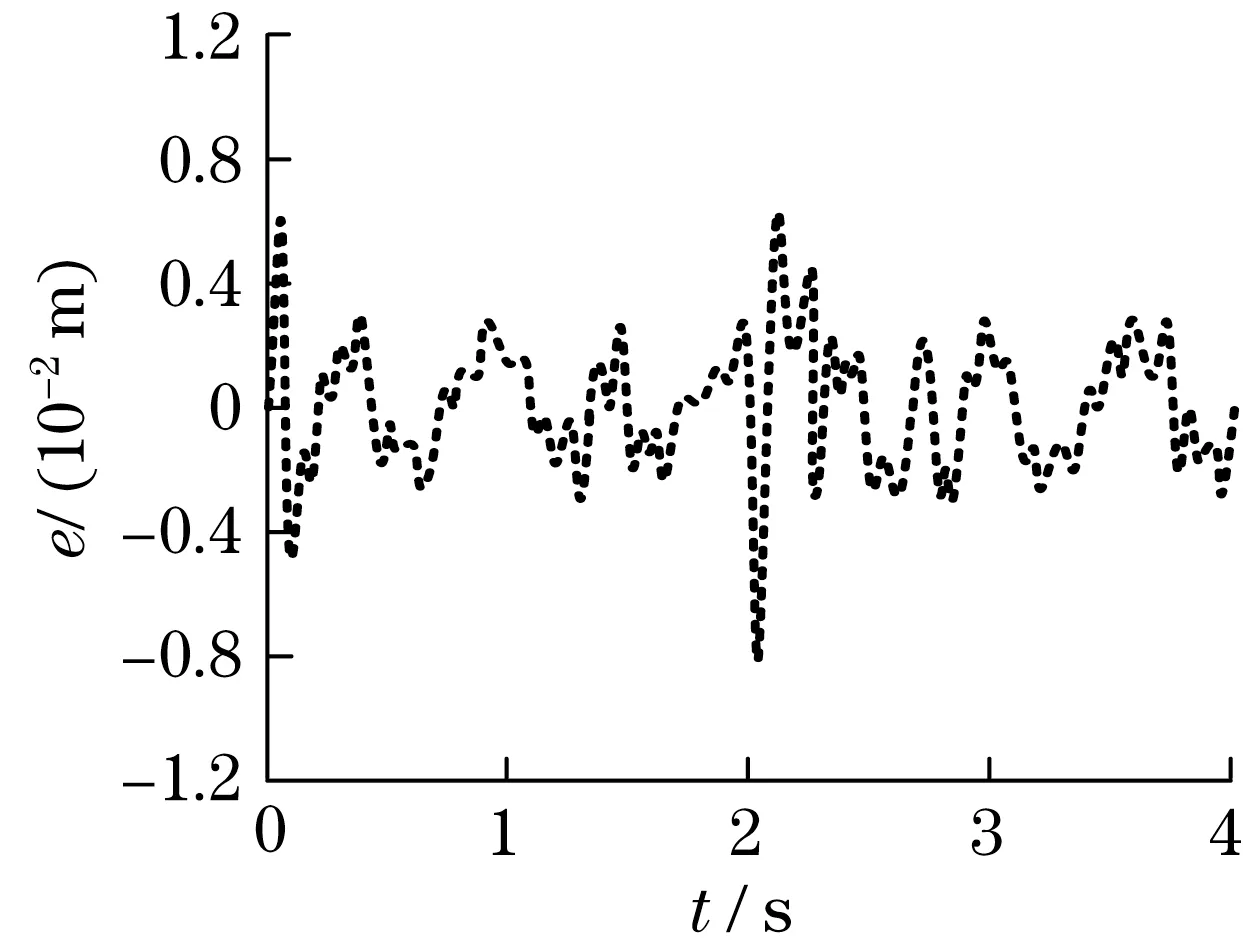
图6 增量式非线性逆控制方法Fig.6 Incremental nonlinear inverse control method

由图5 和图6 可知，如果机器人末端执行器期望信号为阶跃信号，采用非线性逆控制方法，机器人末端执行器产生的最大误差为1.39×10-2m，当控制系统处于稳定状态时，其误差在［-0.5×10-2， 0.5×10-2］ m 范围内。而采用增量式非线性逆控制方法，机器人末端执行器产生的最大误差为0.8×10-2m，当控制系统处于稳定状态时，其误差在［-0.3×10-2， 0.3×10-2］ m 范围内。同等条件下，通过输出误差对比，采用增量式非线性逆控制方法，机器人末端执行器输出误差较小，能够提高机器人末端执行器追踪精度。

4 结论

针对6 自由度液压机器人末端执行器运动轨迹跟踪误差较大问题，设计了增量式非线性逆控制的液压系统，通过仿真验证末端执行器跟踪效果，主要结论如下。

（1） 采用非线性逆控制方法，6 自由度液压机器人末端执行器跟踪误差较大，而采用增量式非线性逆控制方法，6 自由度液压机器人末端执行器跟踪误差较小。

（2） 采用Matlab 软件对机器人末端执行器跟踪误差进行仿真，可以检验不同控制方法输出效果，为设计人员提供参考资料，避免控制方法设计不当而造成控制系统输出精度下降。