液压驱动型水下掘进机器人臂架运动控制研究

刘修成，董奇峰，纪晓宇，范晨阳，孟林园

（1.中交第二航务工程局有限公司 技术中心，湖北 武汉 430040； 2.长大桥梁建设施工技术交通行业重点实验室，湖北 武汉 430040； 3.燕山大学 机械工程学院，河北 秦皇岛 066004）

液压驱动型机器人综合机械、液压、电气、控制等多学科领域的先进技术，因其具有负载能力强、响应速度快、控制精度高及功率重量比大等优点被广泛应用于工业制造、医疗服务、工程建造等技术领域［1-5］。串联机械臂作为液压驱动型机器人的重要分支，其运动控制因应用需求不同而成为该技术领域的重要研究方向。

在液压机械臂运动控制中，主要目的是根据所规划的运动轨迹执行特定的任务。其中，轨迹规划根据任务属性而制定，轨迹跟踪由液压控制系统完成。覃艳明等［6-7］针对八自由度液压凿岩机器人任务需求，使用D-H 法求解机器人正、逆运动学方程，在关节空间内采用五次多项式算法进行轨迹规划，并基于串级自抗扰控制器进行轨迹跟踪控制；王亚丽等［8-9］为实现五自由度光伏板清洁机器人液压机械臂的精准运动控制，基于D-H法和几何法求解机器人运动学描述方程，使用比例-积分-微分（proportional integral derivative，PID）控制器对臂架电液比例控制系统进行校正；黄振东等［10］根据3 自由度清污机器人液压机械臂工作中路径重复的特点，基于几何法求解机器人正、逆运动学模型，使用位置反馈结合速度前馈的控制方法对电液控制系统进行优化。

上述学者基于各自工程领域的任务特点，对机器人液压臂架运动控制的研究均取得了较好的应用效果。水下掘进机器人臂架主要应用于沉井施工中刃脚位置的取土作业，本文根据其作业特点对其进行运动控制研究。

1 运动学分析

1.1 总体结构与作业流程

水下掘进机器人总体结构如图1 所示，伸缩机械臂内置伸缩油缸，可由摆幅油缸驱动围绕其与摆幅基座的铰接点进行回转运动，同时摆幅基座由回转驱动控制可绕中心轴线进行回转运动。机器人臂架各关节驱动方式均为液压驱动，为3 自由度机械臂。

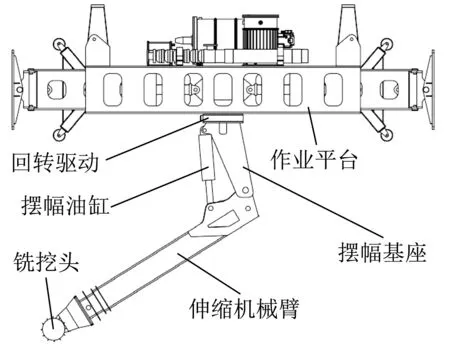
图1 水下掘进机器人结构Fig.1 Structure of underwater tunneling robot

为有效清理沉井刃脚位置的土层，水下掘进机器人需控制铣挖头深入刃脚下方进行铣挖作业，主要作业流程如图2 所示。首先为初始状态：铣挖作业初始状态如图2（a）所示，此时摆幅油缸处于最大行程状态，伸缩机械臂处于最小行程状态；其次为下挖运动：摆幅油缸不动作，伸缩机械臂伸长指定距离，如图2（b）所示；然后为摆幅运动：伸缩机械臂不动作，摆幅油缸缩回指定距离，直至铣挖头伸至刃脚下方，如图2（c）所示；最后为重置运动：摆幅油缸不动作，伸缩机械臂缩回至最小行程状态，结束一轮铣挖作业，如图2（d）所示。摆幅基座转动180°，重复上述流程可对另一侧刃脚下方进行铣挖作业。

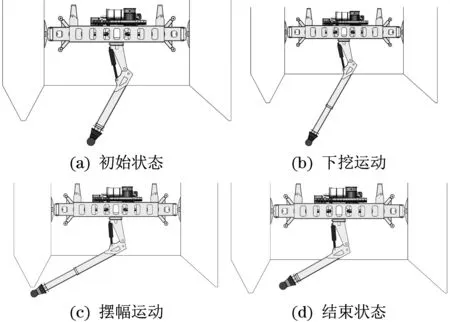
图2 作业流程Fig.2 Operation process chart

水下掘进机器人取土作业中，铣挖头需按照预定轨迹进行运动，不仅需铣挖到位，还要避免碰触刃脚，因此需要对铣挖头进行精确、稳定的运动规划和控制。

1.2 运动学模型

水下掘进机器人执行臂架第1 个关节绕回转驱动轴线运动时，对取土作业平面内的运动无影响，因此可简化为2 自由度机械臂，建立其D-H 坐标系，如图3 所示。其中，基坐标系｛0｝Y0轴垂直于纸面向里，坐标系｛1｝Z1轴垂直纸面向外，坐标系｛2｝Y2轴垂直纸面向外，工具坐标系｛h｝与坐标系｛2｝重合；θ1为杆件转角，a0、a1、d2为杆件尺寸，C为X1轴与Z2轴交点。

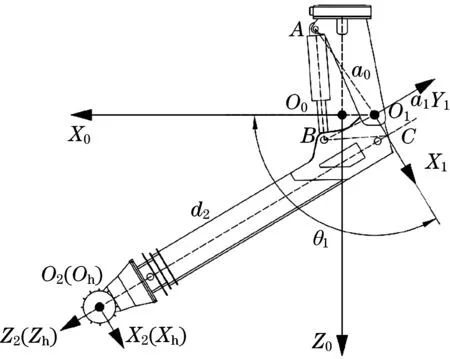
图3 臂架D-H坐标系Fig.3 The D-H frame of the boom

根据连杆参数和坐标系可得D-H 参数，见表1。

表1 水下掘进机器人臂架D-H参数表Tab.1 D-H parameter table of boom

根据D-H 坐标系和D-H 参数表可得各连杆间齐次变换矩阵。其中，相邻坐标系间齐次变换矩阵为

关节2坐标相对于基坐标系位姿矩阵为

代入表1参数，可得

式中：c1=cosθ1，s1=sinθ1。

由于工具坐标系｛h｝与坐标系｛2｝重合，则臂架末端铣挖头坐标相对于基坐标系位姿矩阵为

式中：x、y、z为铣挖头坐标系原点相对于基坐标系的位置坐标；ϕ为铣挖头姿态角。

由臂架运动学正解式（4）可得其反解为

水下掘进机器人执行臂架由摆幅油缸和伸缩油缸调整2 个关节的运动，因此，各关节运动可转换为对应油缸的运动。设摆幅油缸初始长度为L1，伸缩量为x1，伸缩油缸伸缩量为x2。其中，AB=L1+x1，关节2为移动关节，d2=3 855+x2。根据几何关系可得

进而可得摆幅油缸伸缩量与关节1转换关系：

各几何参数为L1=930.0 mm，AO1=1 200.5 mm，BO1=650.0 mm，∠BO1C=94°。

1.3 轨迹规划

轨迹规划是机械臂运动轨迹控制的基础，主要包括在笛卡尔空间和关节空间内的轨迹规划方法。其中，关节空间内的轨迹规划方法只需知道各关节始、末位姿即可规划出所需路径，且具有计算量小、可避免机器人奇异性问题等优点［11］。结合水下掘进机器人臂架作业特点，采用关节空间内的轨迹规划方法。

轨迹规划算法的选取对臂架运动性能有着重要意义，其中，五次多项式算法能够对关节运动始、末角度，角速度和角加速度进行约束，有利于臂架作业的平稳性和安全性。设臂架关节运动始、末时间分别为t0和tf，始、末位移分别为θ0和θf，则五次多项式插值函数可表示为

式中：分别为角度、角速度和角加速度约束函数，其中，θ（t0）=θ0，θ（tf）=θf。

式中：α=θf-θ0。

摆幅油缸和伸缩油缸位移可根据与对应驱动关节之间的几何关系转换为五次多项式位移函数，因此，可将关节内的轨迹规划转换到驱动空间，从而控制液压油缸进行轨迹跟踪控制。

2 轨迹跟踪控制系统

由运动学分析可知，作业过程中，水下掘进机器人铣挖头的运动轨迹控制最终转换为摆幅油缸和伸缩油缸的位移控制。臂架控制系统为电液比例位置控制系统，该系统是一种时变性、非线性系统，且存在着不确定的扰动因素，为实现较好的轨迹跟踪效果，采用模糊PID控制。

2.1 电液比例控制系统线性模型

电液比例位置控制系统结构如图4 所示，其中，液压缸伸缩量通过位移传感器反馈至比较器，与给定信号比较后，控制器通过比例阀对液压缸进行纠偏控制，进而使液压缸沿给定信号进行运动。铣挖头在作业过程中对液压缸造成的负载质量和受力变化可统一作为系统的外部干扰。

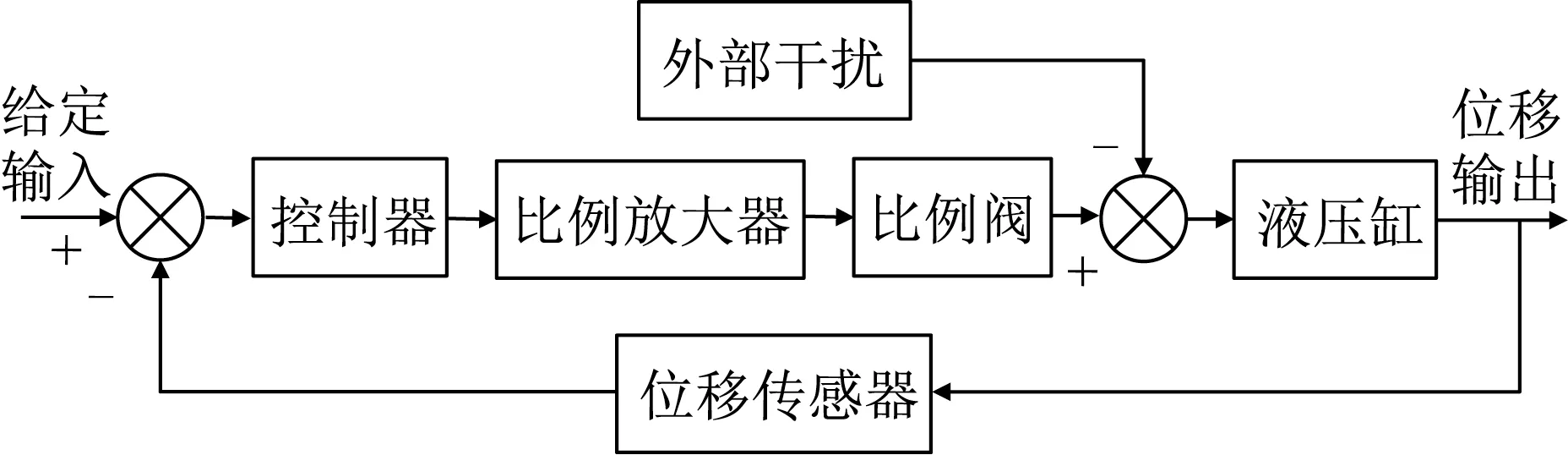
图4 控制系统结构Fig.4 Structure of control system

电液比例阀控非对称液压缸位置控制系统模型如图5所示［12］，图中，Ka为比例放大器增益，Ksv为比例阀增益，ωsv为比例阀频率，ξsv为比例阀阻尼比，Kq为比例阀流量增益，Ap为有效油缸面积，Kce为总流量压力系数，V为液压缸总容积，βe为液压油有效体积弹性模量，ωp为液压固有频率，ξp为液压阻尼比系数，Kx为位移传感器增益，各参数值见表2。

表2 阀控缸系统参数Tab.2 Parameters of valve-controlled cylinder system

图5 电液比例位置控制系统模型Fig.5 Model of electro-hydraulic proportional position control system

2.2 模糊PID控制器设计

模糊PID 控制是将模糊控制和PID 控制相结合的一种控制方法，基于一定模糊规则对PID 控制器的3 个参数进行实时优化，能够适应存在时变性、非线性等模型多变的控制系统，因此其控制效果要优于常规PID 控制［13］。模糊PID 控制原理如图6 所示，其中，e、ec分别为系统偏差和偏差变化率，经模糊化和模糊推理后得到修正参数ΔKP、ΔKI和ΔKD，从而实现对PID 控制器KP、KI和KD参数的实时调整。

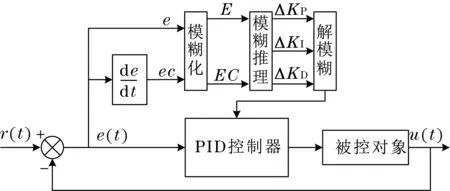
图6 模糊PID控制原理Fig.6 Schematic of fuzzy PID control

将变量e、ec、ΔKP、ΔKI和ΔKD的论域离散为{NB，NM，NS，ZO，PS，PM，PB}7 个子集，分别表示为负大、负中、负小、零、正小、正中和正大。各变量采用三角形隶属度函数，取值范围和控制器模糊规则见文献［14］。

2.3 仿真分析

在Matlab/Simulink 环境下，搭建基于模糊PID 的阀控缸电液比例位置控制系统模型，检验所设计控制器的控制效果。为验证系统的响应速度，输入幅值为0.1 m 的阶跃信号，仿真结果如图7 所示。由图7 可知，经模糊PID 校正后，摆幅油缸调整时间为0.42 s，相较于校正前响应速度提高了96.7%且系统无超调；伸缩油缸调整时间为0.38 s，相较于校正前响应速度提高了95.5%，且系统无超调。

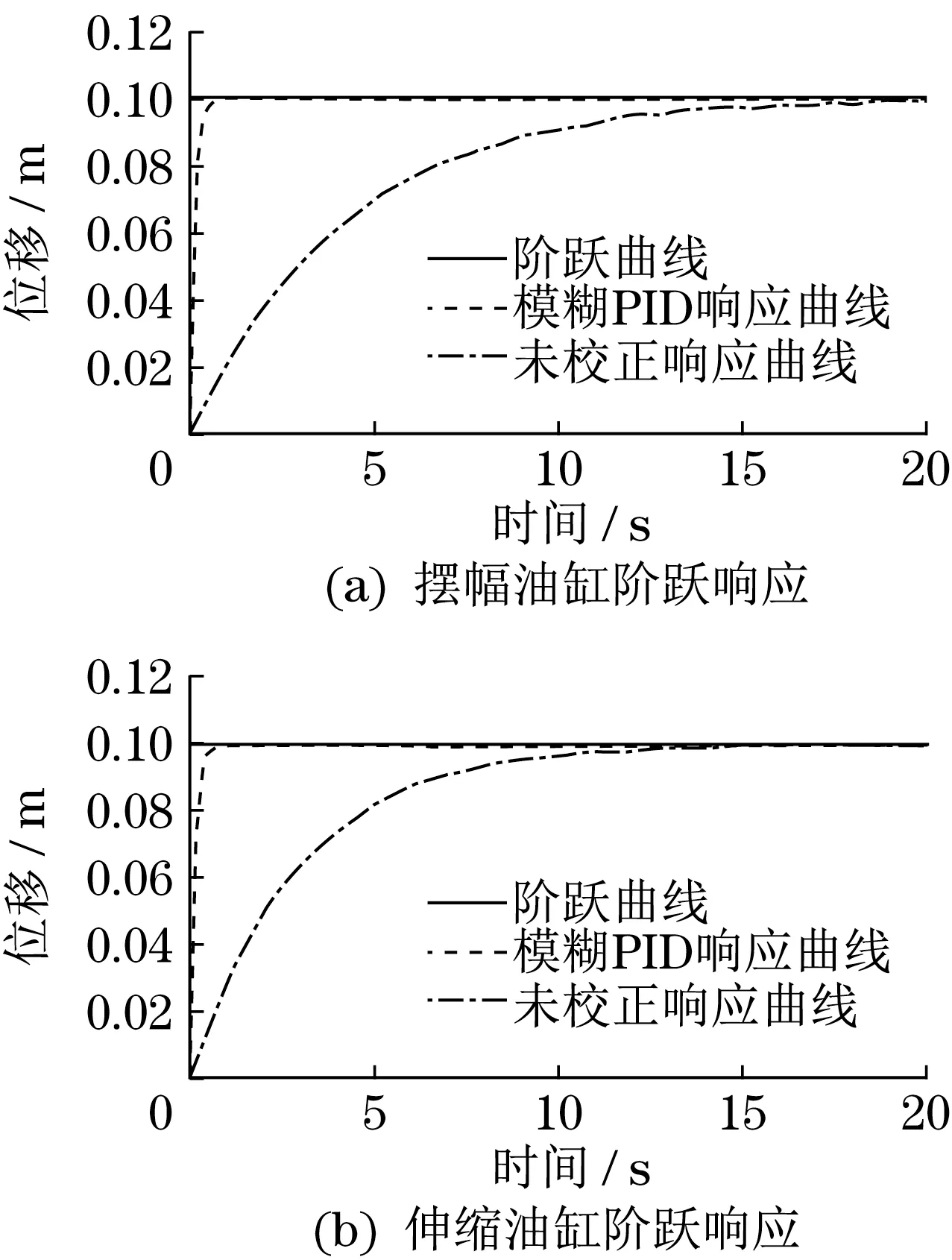
图7 阶跃响应曲线Fig.7 Step response curve

为验证系统的跟随精度，输入斜率为0.01 m/s的斜坡信号，仿真结果如图8所示。由图8可知：经模糊PID 校正后，摆幅油缸最大跟随误差为1.7 mm，相较于校正前跟随精度提高了95.9%；伸缩油缸最大跟随误差为1.8 mm，相较于校正前跟随精度提高了93.0%。

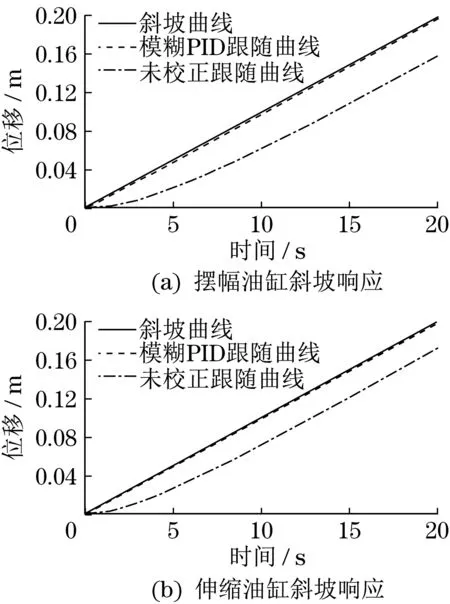
图8 斜坡响应曲线Fig.8 Slope response curve

由仿真分析可知，系统加入模糊PID 控制器后，系统响应速度和跟随精度均得到了较大提升。

3 臂架轨迹运动控制试验

为验证模糊PID 控制器的实际控制效果，在水下掘进机器人实验平台进行应用试验，如图9所示。

图9 实验平台Fig.9 The experimental platform

分2 个阶段分别对伸缩油缸和摆幅油缸进行试验：第1 阶段，伸缩臂伸长量由0.10 m 伸长至0.50 m，耗时50 s；第2 阶段，摆幅油缸伸长量由0.64 m 缩回至0.34 m，耗时100 s。采用5次多项式算法对油缸运动进行轨迹规划后，进行轨迹跟踪控制，试验结果如图10所示。

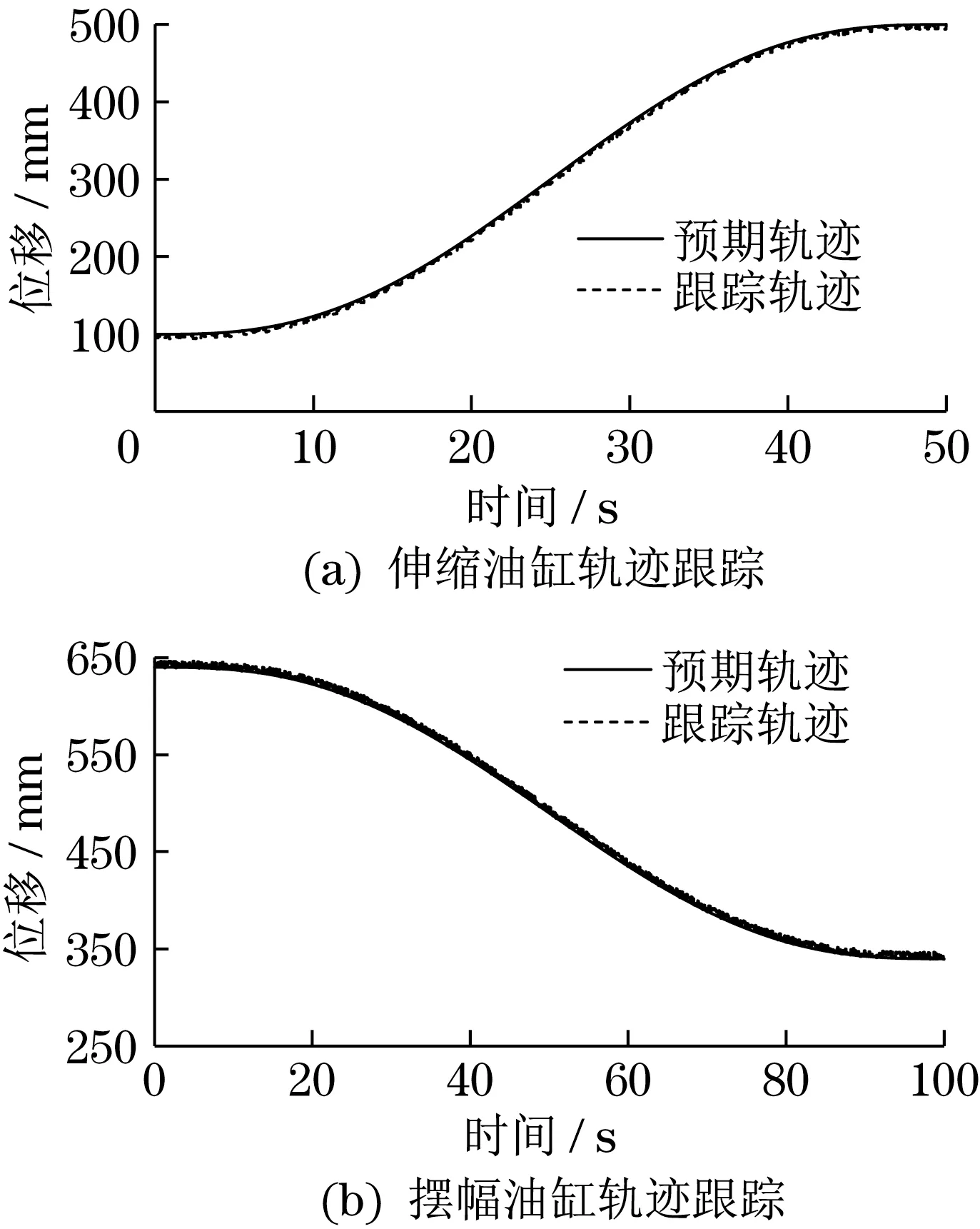
图10 轨迹跟踪曲线Fig.10 Trajectory tracking curve

由试验结果可知，在实际取土作业中，臂架轨迹控制精度虽然受到内、外部非线性因素干扰的影响，伸缩油缸轨迹跟踪误差为7.3 mm，摆幅油缸轨迹跟踪误差为6.9 mm，但误差均小于10.0 mm，符合使用要求，证明了轨迹规划算法、轨迹跟踪控制算法的有效性和实用性。

4 结语

本文根据水下掘进机器人臂架作业运动特点，对其进行轨迹规划和轨迹跟踪控制研究，通过理论分析、仿真和试验研究，得出如下结论：机器人臂架取土作业每个流程均为始、末关节角度已知的运动，且无须考虑中间点轨迹，考虑臂架运动的稳定性，采用关节内5 次多项式轨迹规划算法对其进行轨迹规划；利用模糊PID 控制器对驱动控制系统进行校正，相较于未校正前，既提高了控制系统的响应速度又提升了跟随精度；取土作业试验结果表明，机器人臂架运动的轨迹规划算法和轨迹跟踪控制算法在实际应用中能达到预期的效果，具有一定的可行性和有效性。