汽车半主动悬架RBF模糊滑模控制器设计及仿真
2023-04-14刘邱祖张建林
刘邱祖,张建林
(太原理工大学 机械与运载工程学院,山西 太原 030024)
磁流变阻尼器具有低能耗、结构可靠、易于控制、快速响应的多项优势,得到广泛使用,尤其是在智能建筑材料、仿生结构等领域发挥了重要作用[1-3]。 磁流变阻尼器(magneto rheological damper,MRD)的传递介质是磁流变液,可通过调节磁流变液剪切屈服应力实现调控的功能。还有学者设计了半主动控制系统,除了可以实现简单结构、低运行成本以及低能耗的优势以外,对于特定工况甚至可以实现主动控制状态下减振性能,目前半主动控制系统已在动力机构、车辆系统等方面不断获得应用推广,市场规模持续扩大[4-5]。
为达到精度控制的效果,首先需要构建准确有效的磁流变阻尼器数学模型作为仿真测试系统[6]。因为MRD 呈现明显非线性滞回的特征,此时对力学模型的选择为是否可获得理想控制性能的关键因素,直接影响模型仿真结果的准确性和效率[7-8]。随着学者对MRD 力学模型的不断研究,分析Bingham 模型可知,受磁流变液黏度影响,产生剪切稀化与稠化的状态,需设置大量模型参数,进而构建对应的逆模型。Wereley 等[9]通过构建模型分析剪切稀化特性,同时,为准确描述MRD 实际的滞回效果,利用Sigmoid 函数对MRD 进行力学性能解析。
另外,合理选择控制策略也是获得优异控制性能的因素。赵强等[10]综合运用模糊控制与滑模控制方法进行测试,发现模糊滑模控制模式具备明显优势。庞辉[11]利用T-S 模糊模型,为主动悬架构建滑模容错调节器。郭存涵[12]在滑模面分析中加入分数阶微积分的处理方法,为模糊分数阶构建主动横向稳定杆算法,经测试表明,该算法可实现汽车侧倾角的精确控制。
基于上述研究,本文为半主动悬架MRD 构建力学模型并对其控制状态进行表征,辨识Sigmoid模型的各项参数。利用天棚阻尼系统建立滑模控制器,选择径向基函数(radial basis function,RBF)神经网络与模糊控制优化控制系统,开展仿真测试。
1 悬架模型
半主动悬架可在控制性能与运行成本间达到最优平衡状态,从模型结构及控制性能层面考虑,为半主动悬架设计1/4 模型时,整体结构较为简单,且可反馈车辆沿垂直方向的动力学性能,使其成为半主动悬架的重要模型结构[13]。半主动悬架构建的1/4 车辆模型与相应的参考模型如图1所示。
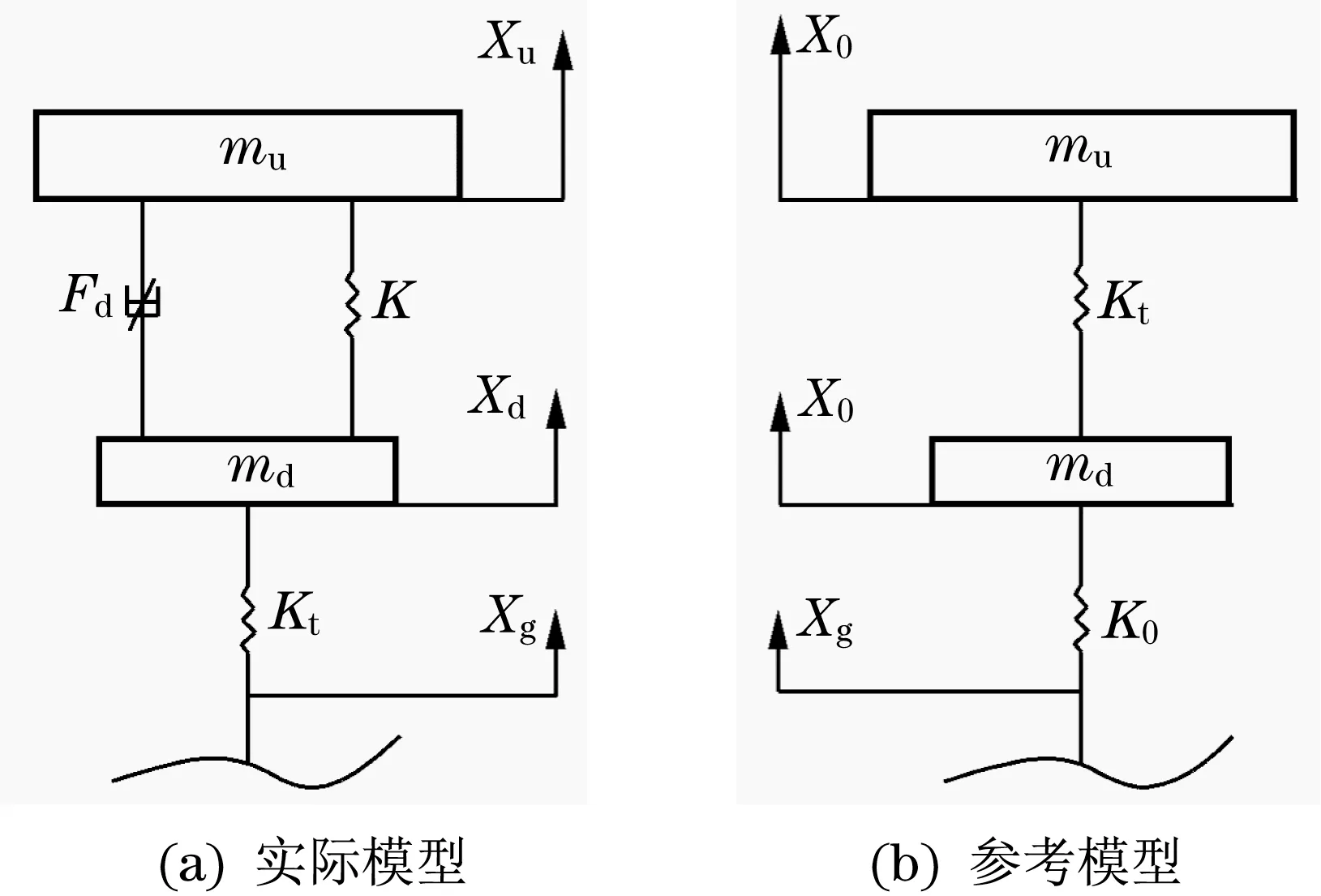
图1 悬架模型Fig.1 Suspension model
由图1 可知,参考模型通过最优控制方法设计,得到具备优异鲁棒性的主动控制策略[9]。本文在牛顿第二定律基础上,构建得到以下动力学方程:
式中:mu为簧载质量,kg;md为非簧载质量,kg;Xu为簧载的位移参数,mm;Xur为簧载的实际位移参数,mm;Xd为非簧载位移,mm;Kt和K分别为对应轮胎的刚度及悬架的刚度,N/m;Xg为路面产生的激励位移,mm;Cdr和Cur为阻尼系数;Fd为MRD 输出阻尼载荷。
2 基于RBF神经网络的滑模控制器
2.1 滑模控制器的设计
式中:e为状态误差矢量,mm。
建立切换函数表达式如下:
式中:A为误差变量项函数;B为误差增量项函数;G为误差调节项函数;Z为误差调节项权重;H为误差波动项函数。
共存在3 项误差矢量,以c表示3 列、1 行向量,表达式为c=[c1,c2,c3],其中,c3取值为1,经过简化后的误差动力学方程如下:
滑动模态方程对应的特征多项式为f(s)=s2+c2s+c1。仅对系统左半平面进行滑动分析,特征根表示为-6±5i,得到c1=55、c2=-12,从而确定c=[55,A-12,1]。
将上述各表达式联立后,得到结果如下:
式中:s为滑膜状态自变量。
随着的时代不断更新,会计工作不再是简单地为企业记账、发放工资等行为。企业启动财务软件等数字化设备为媒介记录公司的各种财务数据,可以让会计人员从单据中解放出来,更多地参与到管理中来。企业披露会计人员制作并经过审核的财务报表以及相关数据信息,股民可以通过企业官网定期发布的各种数据、新闻等了解企业的经营状况。一旦大型企业的经营者为了追求利益而无视法律让财务人员进行违规操作,将会造成市场混乱、股市震荡等后果,使股民的利益受损、行业的发展受到阻碍。此时,会计行为带来的职业风险对社会、行业的危害将是无法估计、难以挽回的。
为确保参考模型与实际模型之间达到最低误差,设定切换函数s导数等于0,因此,计算模控制器输出阻尼力如下:
式中:Feq为等效阻尼力,N。
分析实际悬架系统运行过程可知,其在运动过程中同时受气体摩擦载荷和悬浮颗粒阻挡的作用,整个系统表现出明显的不确定性变化规律。为降低外界干扰影响,增强滑模运动控制性能,为系统构建优化滑模控制方式。
按照等速趋近方式建立模型表达式如下:
式中:sgn()为取值0 或1 的符号函数;ξ为调节系数。
其中,ξ大小直接影响滑模面速度,当该值较大时,可在更短时间内到达滑模面,但会引起更明显抖振现象。结合前面各项因素的综合影响,获得滑模控制力如下:
式中:ms为取决于s的系数;sgn(s)为符号函数;Fe为等效输出阻尼力,N;Fs为滑模实际控制力,N。
设置约束条件后得到方程式如下:
式中:Fd为MRD输出阻尼载荷。
2.2 RBF神经网络滑模控制器优化
通过上述推导可知,RBF神经网络会形成复杂的控制状态,此时无法仅通过Simulink模块达到控制的效果,本文选择S函数与Simulink 开展联合测试,得到联合仿真流程,如图2所示。

图2 滑模变控制RBF神经网络优化流程Fig.2 Optimization flow chart of sliding mode control RBF neural network
设置仿真参数b=15.0、y=1.3,动量因子α为0.05,学习速率x=0.15,输入1 列2 行向量,以5 列2行向量作为径向基参数,结合之前仿真分析结果,确定切换函数s取值区间为[-0.03,0.03],对切换函数求导得到的s介于[-0.3,0.3],因此设定径向基参数中心如下:
从1~5 之间随机选择网络初始权值,对于S函数,通过Persistent 函数设置持久变量w、b和ci,并把计算结果保留至函数调用内层,更新权值wi。
2.3 滑模控制器模糊优化
采用不同控制策略测试滑模控制器优化的性能,本研究选择模糊控制方式,实现不同增益参数的切换。采用模糊控制方式分析时,以人工经验作为依据;以模糊理论作为分析基础时,无须为被控对象构建精确数学模型,也较易被使用者接受,同时具备优异适应性,因此在各类控制系统中,得到推广应用。
采用模糊控制时,通过双输入单输出方式实现,输入项为s和s0,依次对应滑动模态距离及其趋向速度,以模糊控制器输出作为增益指标,实现以模糊控制方式进行增益切换的功能。结合前期仿真结果,设置较小切换函数s和s0,提升滑模控制器的稳态性能,为避免滑模控制器与稳态方式偏离的问题,按照s<0、s0<0 的原则建立模糊规则,相关数据见表1。设置模糊语言变量{NB,NM,ZO,PM,PB},建立三角函数计算隶属度。NB 表示非常不可能,NM 表示不太可能,ZO 表示可能,PM 表示很可能,PB表示非常可能。
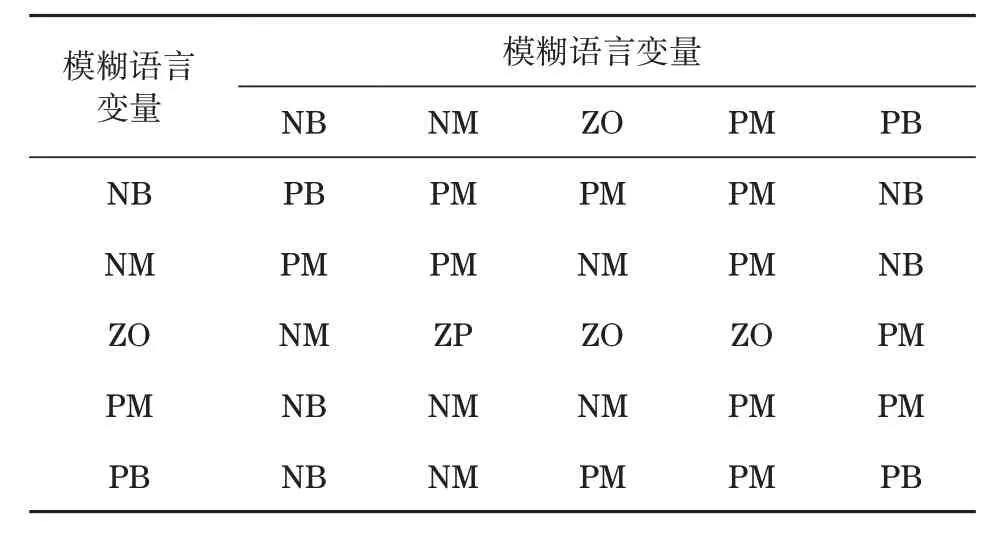
表1 模糊控制规则Tab.1 Fuzzy control rules
3 仿真结果分析
本文设计2 种控制策略优化增益系数,利用饱和函数取代符号函数验证优化策略的可靠性。对本文各控制器进行测试比较,仿真测试10 s,获得半主动悬架1/4模型的簧载运动参数与悬架振动速度,簧载速度、加速度和悬架振动速度测试情况如图3 所示。同时计算仿真参数的均方根数据。由图3 可知,采用3 种控制模式进行控制性能测试的结果。
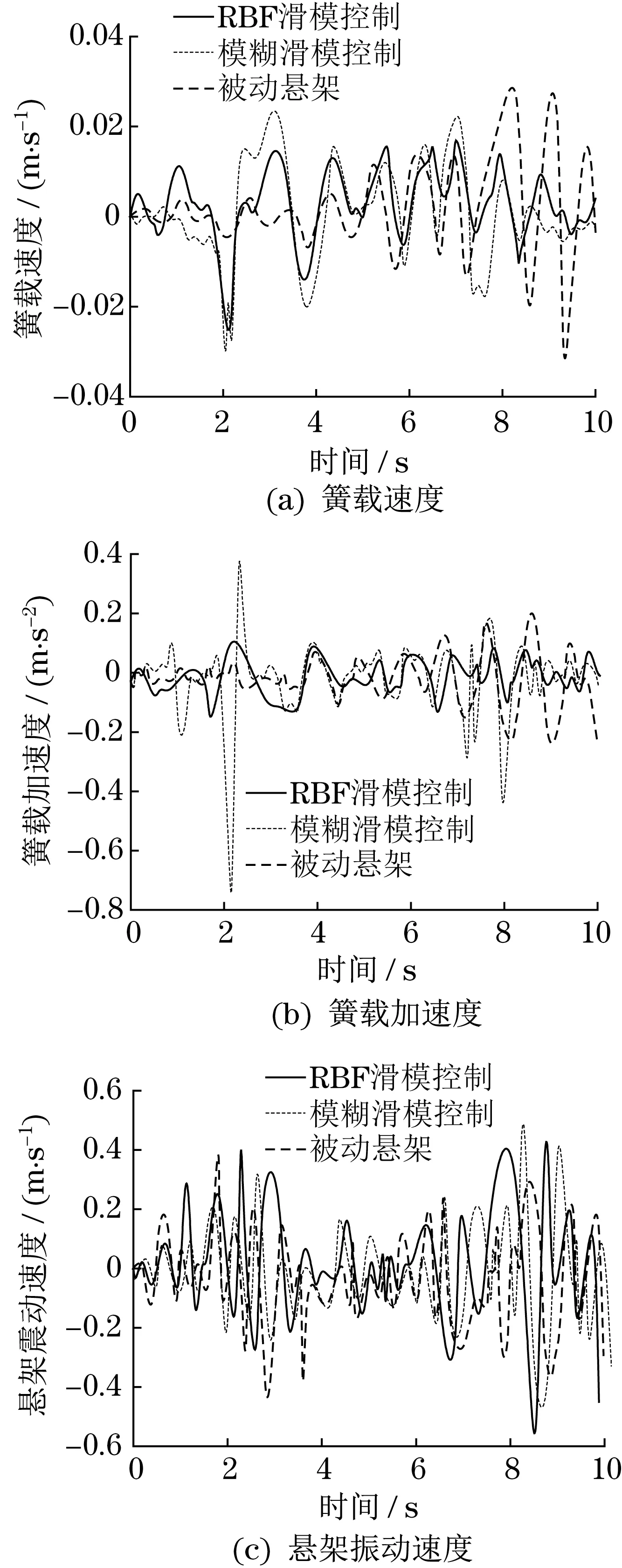
图3 悬架性能指标Fig.3 Suspension performance index
由图3(a)和图3(b)可知,模糊滑模控制条件下,簧载速度与加速度形成比RBF 滑模控制方式更大的峰值,模糊滑模控制还会造成激变,严重影响车辆乘坐舒适度,增加操控难度。由图3(c)可知,不同控制模式的悬架振动速度虽然存在一定的偏差,但总体变化趋势一致,经综合对比发现,RBF神经网络达到了最优控制效果。
各控制策略下,对悬架性能指标进行均方根计算,结果见表2。由表2 可知,与被动悬架的簧载速度和加速度相比,RBF 滑模控制和模糊滑模控制方式均有明显减小,悬架振动速度基本相近。
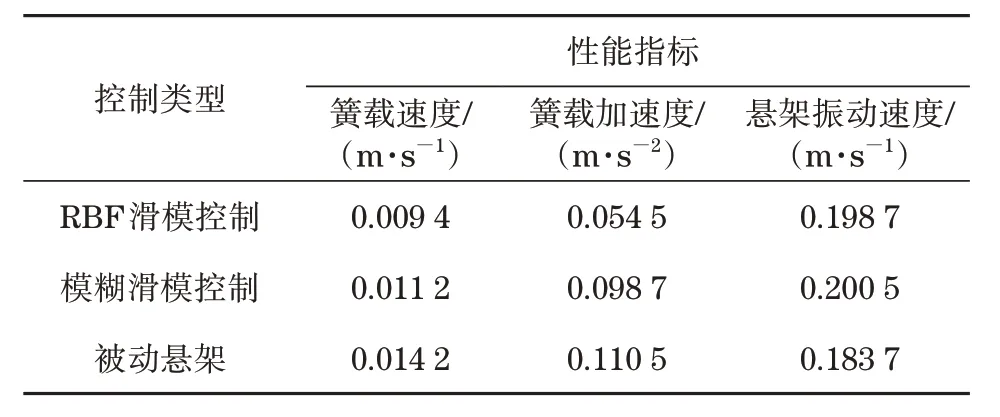
表2 悬架性能指标均方根Tab.2 Suspension performance index root mean square
4 结论
(1) 悬架系统表现出明显的不确定性变化规律,为增强滑模运动控制性能,构建优化滑模控制,采用模糊控制方式构建精确数学模型。
(2) 模糊滑模控制条件下,簧载速度与加速度形成比RBF 滑模控制方式更大的峰值,存在一定的偏差,但总体变化趋势一致,对比发现RBF 神经网络达到了最优控制效果。
(3) 与被动悬架的簧载速度和加速度相比,RBF滑模控制和模糊滑模控制方式均有显著减小,悬架振动速度基本相近。
