基于粒子群算法和变分模态分解的起重机滚动轴承性能退化评估
2023-04-14陆后军孙跃峰
陆后军,张 飞,孙跃峰
(上海海事大学 物流工程学院,上海 201306)
滚动轴承是机械设备的核心部件之一,对设备状态和寿命影响较大[1],及时准确评估滚动轴承退化对设备安全稳定运行至关重要。带故障滚动轴承的振动信号为非线性、非平稳,且噪声复杂[2],使得故障特征的提取具有挑战性。
变分模态分解(variational mode decomposition,VMD)是一种新的自适应时频分析方法,用于分离信号频率成分。艾红等[3]使用小波包变换诊断水泥回转窑轴承故障。夏均忠等[4]将最大相关峭度解卷积和VMD 方法应用于滚动轴承故障特征提取。赵玮[5]将VMD 与快速谱峭度方法联合应用于故障类型判断。马洪斌[6]以模态分量包络熵为适应度函数,通过蛙跳算法优化参数处理故障诊断。丁承君[7]使用粒子群(particle swarm optimization,PSO)算法全局寻优径向基神经网络参数,用于压缩机故障诊断。
本研究通过PSO改进VMD,将多特征融合后输入向量数据描述(support vector data description,SVDD)模型,定量评估滚动轴承性能退化。验证结果表明,该方法准确描述轴承性能退化,相较于其他方法具有优势。
1 变分模态分解原理
假设VMD 每个模态函数都有不同中心频率的带宽,中心频率的带宽随算法的迭代而更新。在各个模态分量互相迭代后,能还原成原始信号的前提条件下,求解出k个估计带宽之和为最小的模态函数uk,表达式如下:
式中:f为原始信号;{uk}={u1,u2,…,uk}为分解后的K个模态分量;ωk为第k个模态分量的频率中心;t为时间。
式(1)为约束变分问题,为求解其最优解,引入二次惩罚因子和Lagrange 乘子构造扩展拉格朗日函数为
式中:α为惩罚因子;λ为Lagrange乘子。
VMD 中采用交替方向乘子法求解以上无约束变分问题,交替更新、和,直到满足迭代停止条件,计算得到约束变分模型的最优解,n+1表示迭代代数。
2 基于粒子群算法优化的VMD(PSOVMD)
PSO 寻找最优解的基本思想是通过种群中不同个体间的协作与信息共享来实现的[8],具有快速收敛的能力,同时也具有良好的全局寻优能力[9]。其算法描述如下:
设Xi=(xi1,xi2,…,xiM)表示M维空间中第i个粒子,粒子以一定速度Vi=(vi1,vi2,…,viM)飞行;pibest=(pb1,pb2,…,pbM)表示经历的最好位置;pigest=(pg1,pg2,…,pgM)表示群体粒子经过的最好位置。
位置和速度的更新公式如下:
式中:c1、c2为学习因子,分别调节向pibest(粒子经历的最好位置)和pigest(群体粒子经过的最好位置)位置的加速权重;r1和r2为在[0,1]范围内的均匀随机数;vid∈[ -vmax,vmax],vmax为常数。
基于PSO 改进VMD 关键参数优化,即利用PSO 优秀的全局寻优能力,并行优化VMD 参数K和α,自适应地选择出最佳的参数组合。利用PSO算法寻优时,需要确定1 个适应度函数,比较当前粒子的适应度及pibest、pigest大小移动粒子的速度和位置。本文选用包络谱峰值因子为指标[10]。
PSO算法优化K和α的流程如图1所示。
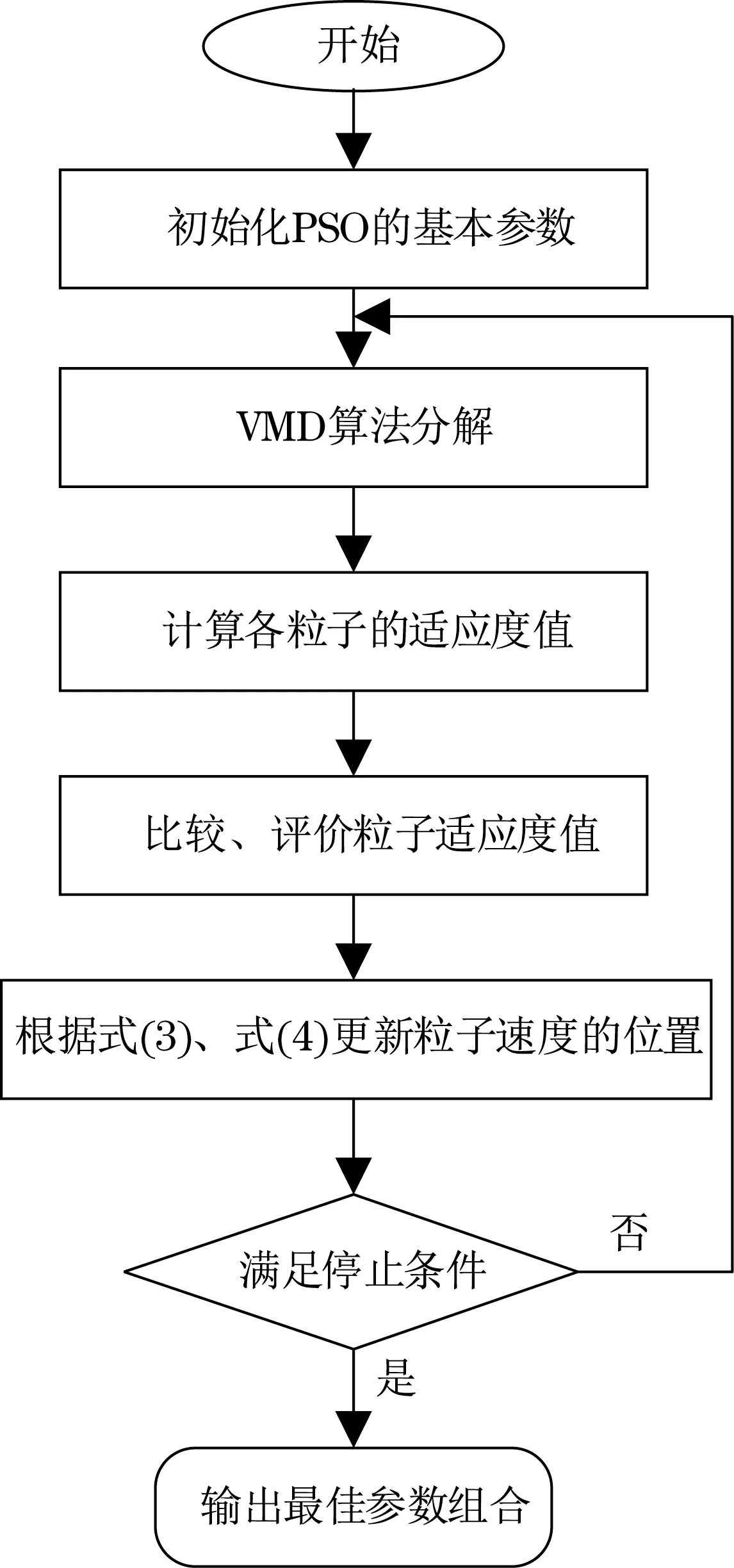
图1 PSO算法优化VMD参数流程Fig.1 PSO algorithm optimization VMD parameter flow chart
(1) 以参数组合(Ki,αi)作为PSO 算法中粒子Xi的位置,初始化各粒子参数。
(2) 基于VMD,在粒子i经过的各位置,即Xi(Ki,αi)分解信号,分解过程中计算每个分量的Ec(包络谱峰值因子),Ec值越大,i粒子在该位置的适应度值越大。
(3) 将当前粒子适应度值与Ppbest、Pgbest的大小进行比较,实现粒子个体及种群极值的更新。
(4) 根据式(6)移动(更新)粒子的速度和位置。
(5) 重复步骤2 和步骤3,直到满足式(6)的判别精度,结束循环,得到粒子的最优解和对应的位置(Ko,αo)。
3 支持向量数据描述
SVDD 是单值分类算法,基于支持向量机理论(support vector machines,SVM)与集成学习结合发展而来[11-13],其功能为实现目标样本与非目标样本的分离,被广泛应用于异常、故障检测等领域。
针对一个目标类样本集{xi,i=1,2,…,n}寻找包含所有或大多数目标类样本的最优超球,该超球由中心c和半径R描述,满足以下优化函数:
式中:C为惩罚参数,控制超球体和误差之间的权衡;ξi为松弛变量,允许一些训练数据在超球体之外。
结合拉格朗日乘子法求解该问题,即在构造拉格朗日函数时,引入拉格朗日乘子αi≥0和γi≥0,如下所示:
对式(9)中的R、c和ξi分别求其偏导,令其等于零,再代入式(8),则式(10)的最小化问题转化为
式中:K(xi,xj)为核函数。
通常在SVDD方法中,选用高斯核函数如下:
式中:σ为宽度参数。
当αi=0 时,样本在超球体内部;当0<αi 超球体半径R等于球心与支持向量xsv的距离,公式如下: 式中:N为终止值。 对于任意样本z,其与超球体球心的距离D的表达式如下: 比较D与R的差异,推断轴承的运行状态。如D≤R,则表示轴承正常;如D>R,则轴承存在故障,且差值越大,故障程度越严重。因此,该方法可有效地评估轴承当前状态。 滚动轴承全寿命周期有正常、轻微退化、严重退化和失效3 个阶段,研究重点为轻微和严重退化。优秀的性能退化特征指标应在各个阶段保持相对稳定,在初始退化阶段具有高敏感性。已有特征指标有时域和复杂度。经分析可知,样本能量、均方根值和样本熵能更准确地反映滚动轴承全寿命周期指标的变化趋势。 滚动轴承从开始正常运行到完全失效全寿命样本,为更好地获取该轴承的性能退化程度,本文提出基于PSO-VMD 和SVDD 结合的性能退化评估方法,流程如图2所示。 图2 轴承性能退化评估流程Fig.2 Flow chart for assessment of bearing performance degradation 其具体步骤如下。 步骤1对每个轴承全寿命周期样本信号进行VMD分解,去除高噪分量,重构其余分量。 步骤2提取重构信号的均方根值、样本能量和样本熵特征,构建轴承性能退化特征矩阵,并进行特征融合。 步骤3以轴承正常状态信号特征为训练样本,使用SVDD 算法训练评估模型,获得超球体参数,包括球心和半径。 步骤4将轴承全寿命周期信号特征作为测试样本,计算每个样本特征到超球体中心的距离,比较距离与超球体半径,得到轴承退化状态曲线和距离的隶属度函数,用作性能退化评估指标。 使用XJTU-SY 轴承数据集[14]进行实验验证,该数据集由西安交通大学和长兴昇阳科技公司合作的机械装备健康监测实验室提供,数据完整地涵盖了滚动轴承从正常运行到失效的完整过程。 在实验中,电机转速为2 250 r/min,施加11 kN径向力于测试轴承。采样频率为25.6 kHz,单次采样时长为1.28 s,每隔1 min 记录1 次数据,共采集533组样本数据。 5.2.1 基于 PSO 得到 VMD 参数K和α 选取轴承早期运动的第60 min 振动信号进行PSO-VMD 分解。最佳分解层数为7,惩罚系数为5 525。适应度函数随PSO 算法迭代次数的变化情况如图3(a)所示。经VMD 分解,每个BIMF 分量的包络谱峰值因子指标如图3(b)所示。 图3 适应度函数与包络谱峰值因子指标Fig.3 Fitness function and peak factor index of envelope spectrum 根据改进PSO-VMD方法特征提取出的滚动轴承振动信号进行重构,轴承全寿命周期信号共有533组样本,每个样本包含32 768个样本点,分别提取每组样本重构信号的样本能量、均方根值及样本熵特征的特征变化曲线,如图4所示。 图4 轴承全寿命周期振动信号故障特征曲线Fig.4 Characteristic curve of vibration signal fault for bearing life cycle 将样本能量、均方根值和样本熵特征进行归一化处理,经分析可知,前120 min 轴承信号特征基本稳定。因此,选用前120 组全寿命轴承信号样本进行SVDD 训练,得到超球体半径R=1.886×10-5。将轴承全寿命周期信号样本输入超球体模型,得到每个样本到球心距离D的变化趋势,如图5所示。 图5 样本到超球体球心距离Fig.5 Sample-to-hypersphere spherical center distance diagram 由图5可知:前127组样本特征在超球体内,表明轴承正常工作;从第128 组样本开始,红色虚线圆圈内的样本特征在超球体外,指示早期轻微故障;直至第354 组样本,样本特征发生显著变化,表明轴承磨损加深,之后变化无规律,表现为严重故障,直至失效。 为定量评估轴承性能退化,引入隶属度函数计算样本特征相对于正常状态的隶属度,得到性能退化指标性能指数(performance index,PI)。 采用降半柯西隶属函数进行计算,表达式如下: 式中:a和b为调整参数,使得PI 在指定范围内分布。 根据上述隶属度函数公式,选取a=165,b=1,得到轴承全寿命周期振动信号的性能退化曲线,如图6所示。 图6 轴承性能退化评估曲线Fig.6 Assessment curve of bearing performance degradation 为进一步证明本文所提方法的优越性,提取有效值、峭度指标、波形指标、峰值指标、脉冲指标和裕度指标这6 个常用的传统时域特征,与前文提出的特征提取方法作对比。使用SVDD算法训练6个时域特征,得到轴承样本至超球体球心距离和轴承性能退化指标,如图7和图8所示。 图7 传统时域特征全寿命样本到球心距离Fig.7 Traditional time-domain feature life-cycle sample to spherical center distance graph 图8 传统时域特征性能退化曲线图Fig.8 Performance degradation curve of traditional time-domain characteristics 由图8 可知,在100~300 min 时,轴承处于初级退化阶段,时域特征表现过于敏感,最后一段时间又趋于稳定变得很小,无法区分性能退化的程度。因此,本文提出的特征提取方法与传统的时域特征提取方法相比,更具有优势。 本文采用PSO-VMD 与SVDD 相结合的方法,对滚动轴承性能进行退化评估,利用轴承全寿命数据验证,对所提出的评估模型进行验证,得出主要结论如下。 (1) 采用基于PSO 的VMD 参数优化方法,对比传统的VMD 分解,克服了凭借经验设置参数的问题,且分解模态的故障特征明显。 (2) 提取重构信号的均方根值、能量和样本熵特征,融合多个特征,充分利用每个特征对轴承信号在不同维度的刻画,结合实验证明对轴承性能退化评估具有更强的敏感性。 (3) 使用传统时域特征指标分析与本文所提出的PSO-VMD 特征提取方法做对比,进一步验证本文方法的优越性。4 结合PSO-VMD 和SVDD 的性能退化评估方法
4.1 特征指标的选择
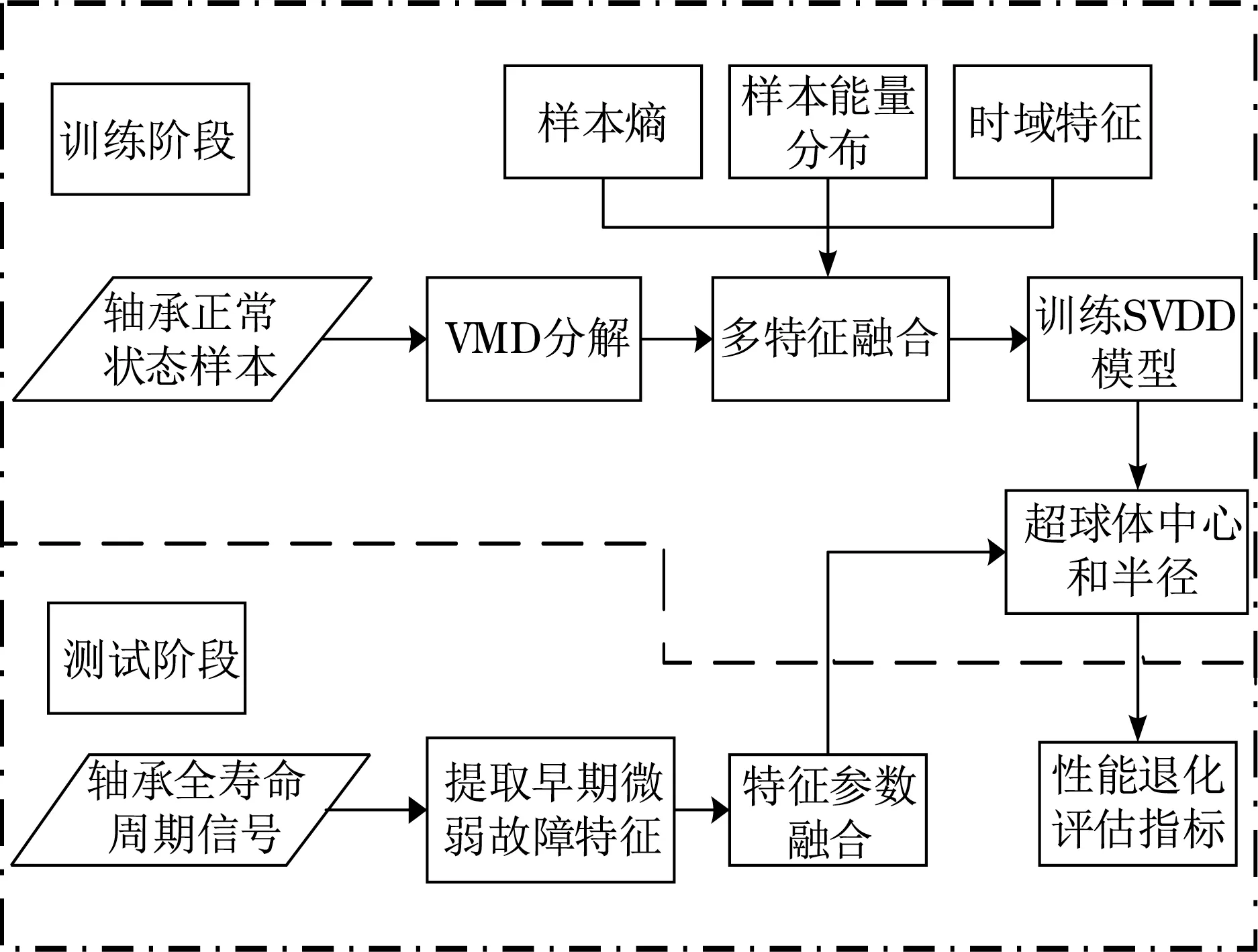
4.2 滚动轴承性能退化程度评估流程
5 实验验证与分析
5.1 实验台介绍
5.2 基于PSO改进VMD的滚动轴承特征提取
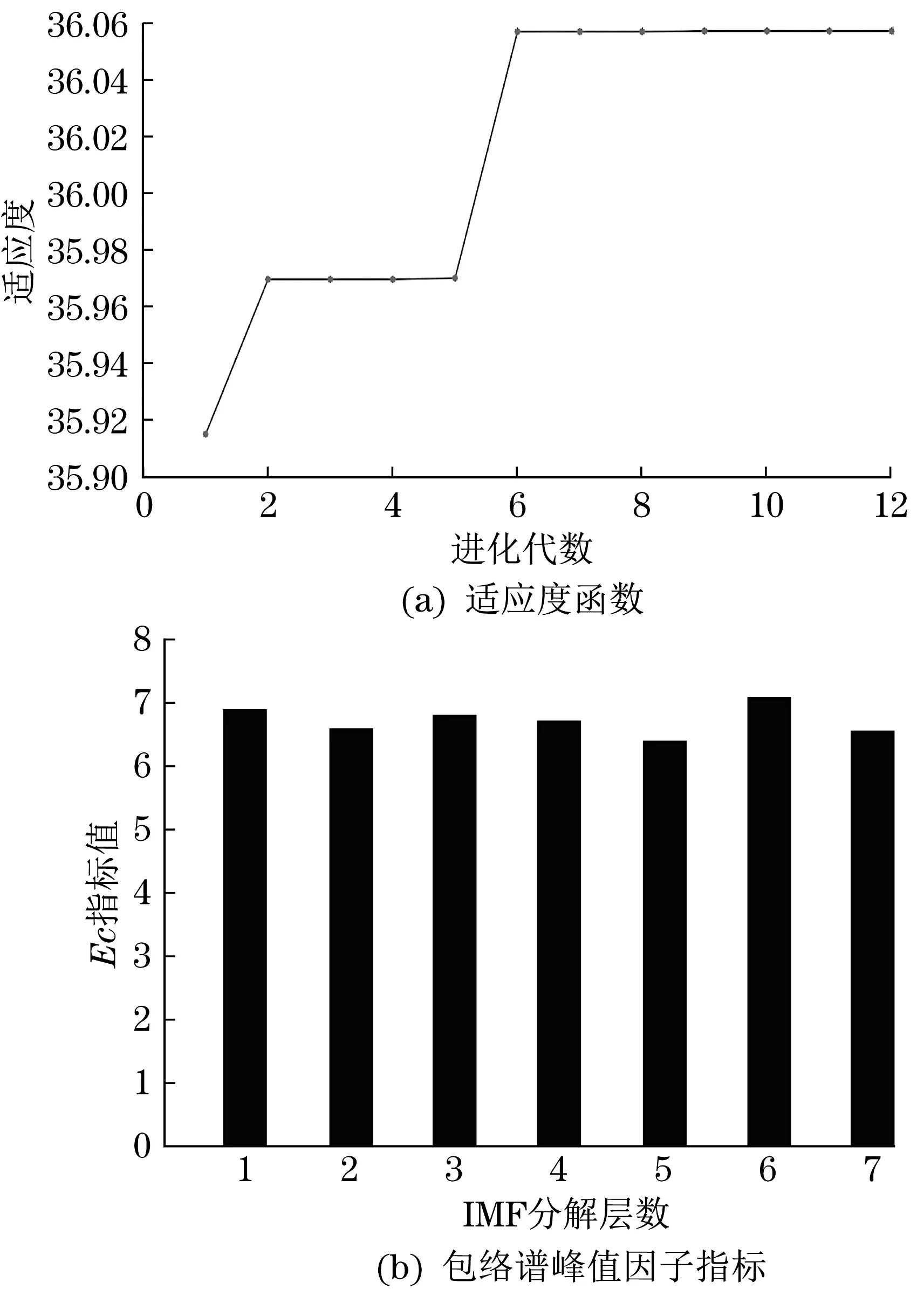
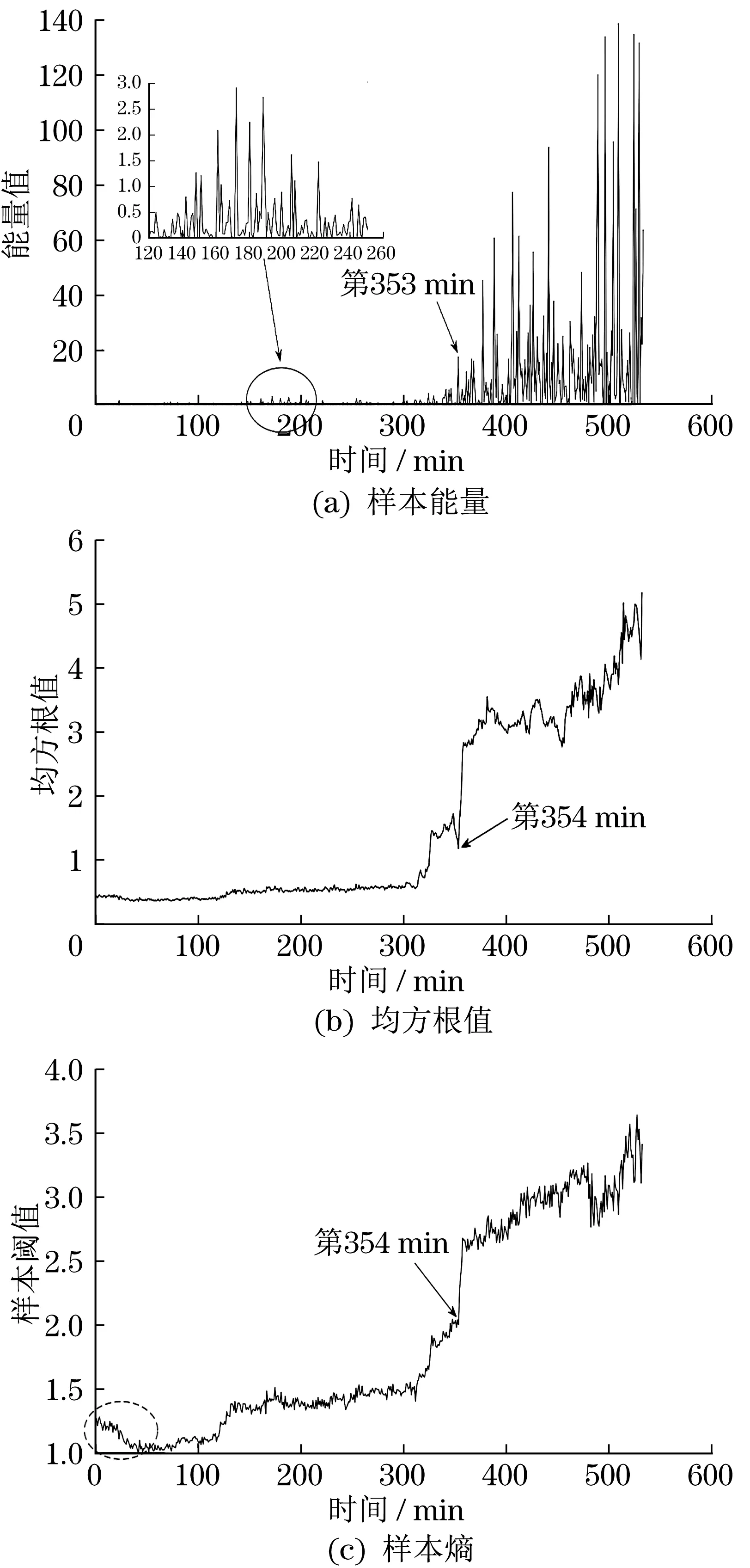
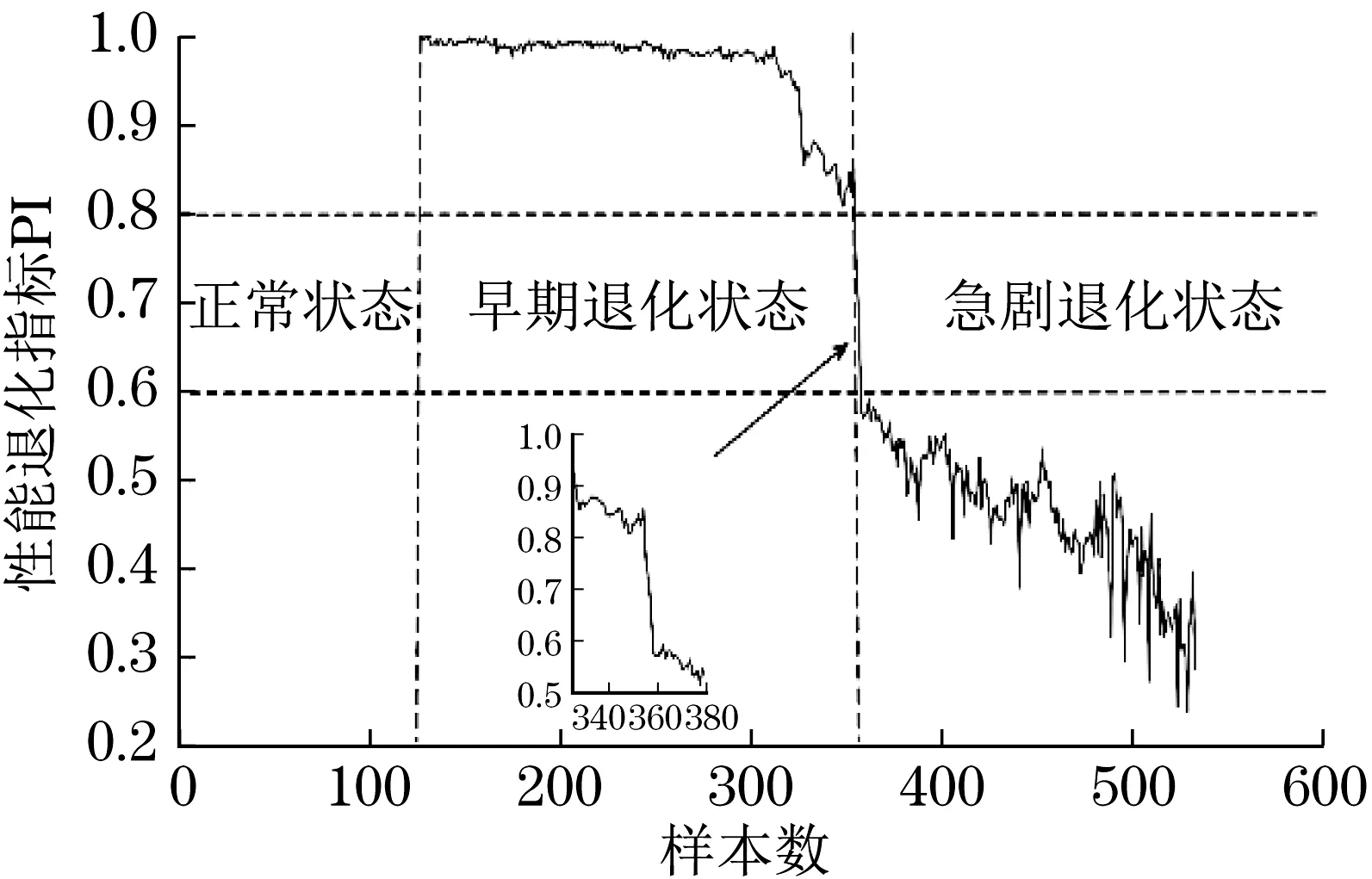
5.3 滚动轴承性能退化评估

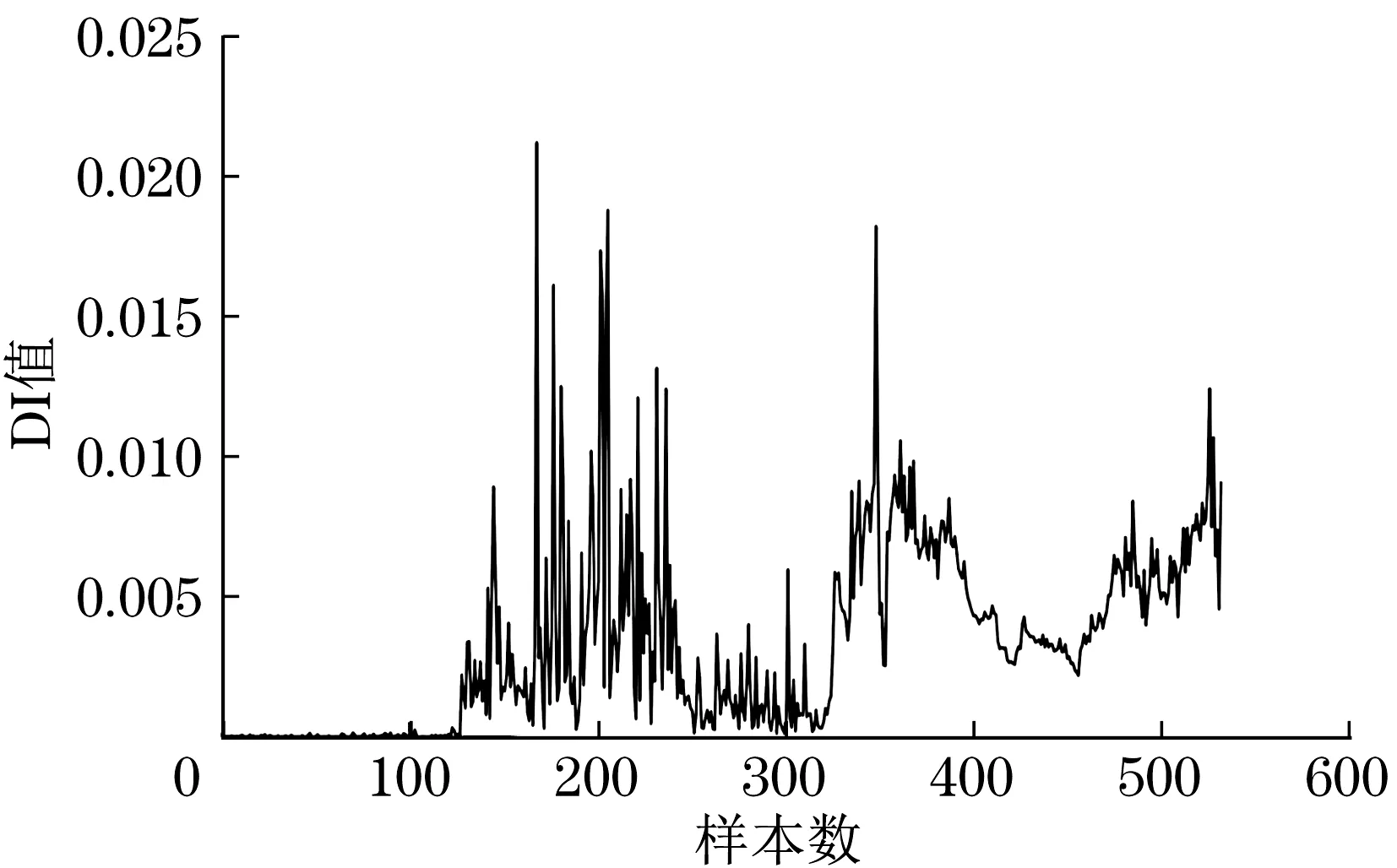
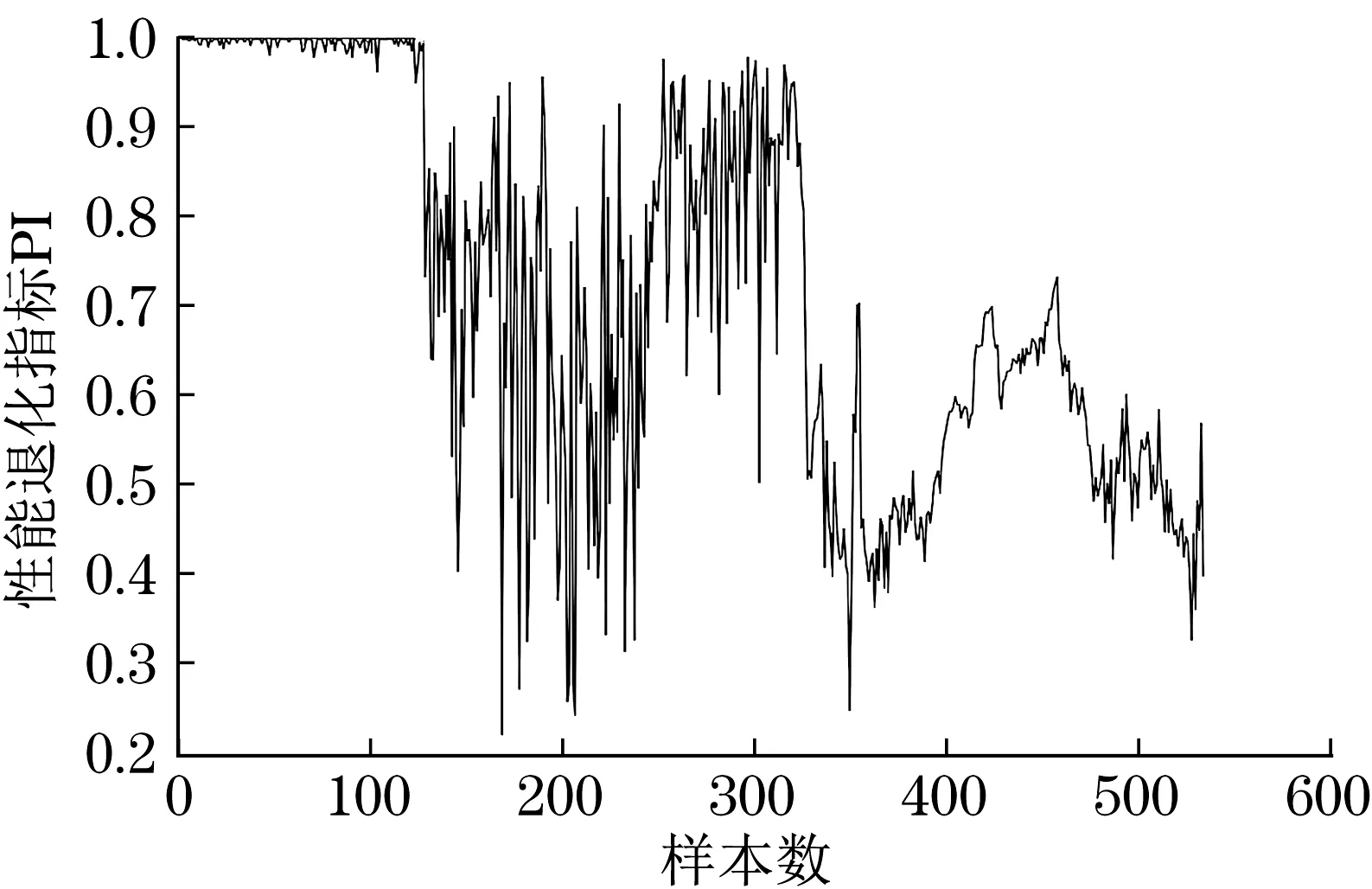
5.4 与传统时域特征指标分析结果的对比
6 结论
