破拆机器人拆除窑衬的时间最优轨迹规划
2023-04-14滕儒民张文帅王大洪
滕儒民,张文帅,王 欣,王大洪
(1.大连理工大学 机械工程学院,辽宁 大连 116023; 2.深圳市先进智能技术研究所,广东 深圳 518049)
破拆机器人常被应用于高粉尘环境下拆除回转窑窑衬,可以提高效率,减少危险事故的发生,提升回转窑的利用率[1]。操作员在操控破拆机器人拆除窑衬时,要反复调整才能准确定位到破拆点[2],破拆点转换费时、费力。另外,自动化和智能化是破拆机器人未来发展的趋势[3],因此对破拆机器人进行时间最优轨迹规划具有重要意义。
段伟雄[4]用3次Bezier曲线对破拆机器人换装属具生成无碰撞路径,对路径上关键点的关节角用5 次多项式拟合,为破拆机器人自动换装属具提供依据。李虹等[5]采用4-3-3-3-4 分段多项式对挖掘机进行轨迹规划,并根据粒子群算法获得时间最优的运动轨迹。洪振宇等[6]在关节空间采用5-3-5 多项式插值规划装载机器人轨迹,并用遗传算法得到时间最优轨迹,该方法运行平稳,可顺利避障。
本文针对破拆机器人拆除窑衬这一工作场景,先用4-3-4 多项式进行轨迹规划,再用改进鲸鱼优化算法优化运动时间,能有效地发挥破拆机器人的运动学性能,提高工作效率。
1 破拆机器人正运动学求解
破拆机器人基本结构如图1 所示,破碎锤通过转台的旋转和4 个油缸的伸缩定位到破拆点。根据基本结构建立关节坐标系,如图2所示。
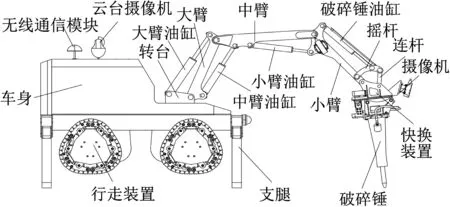
图1 破拆机器人基本结构Fig.1 Basic structure of demolition robot
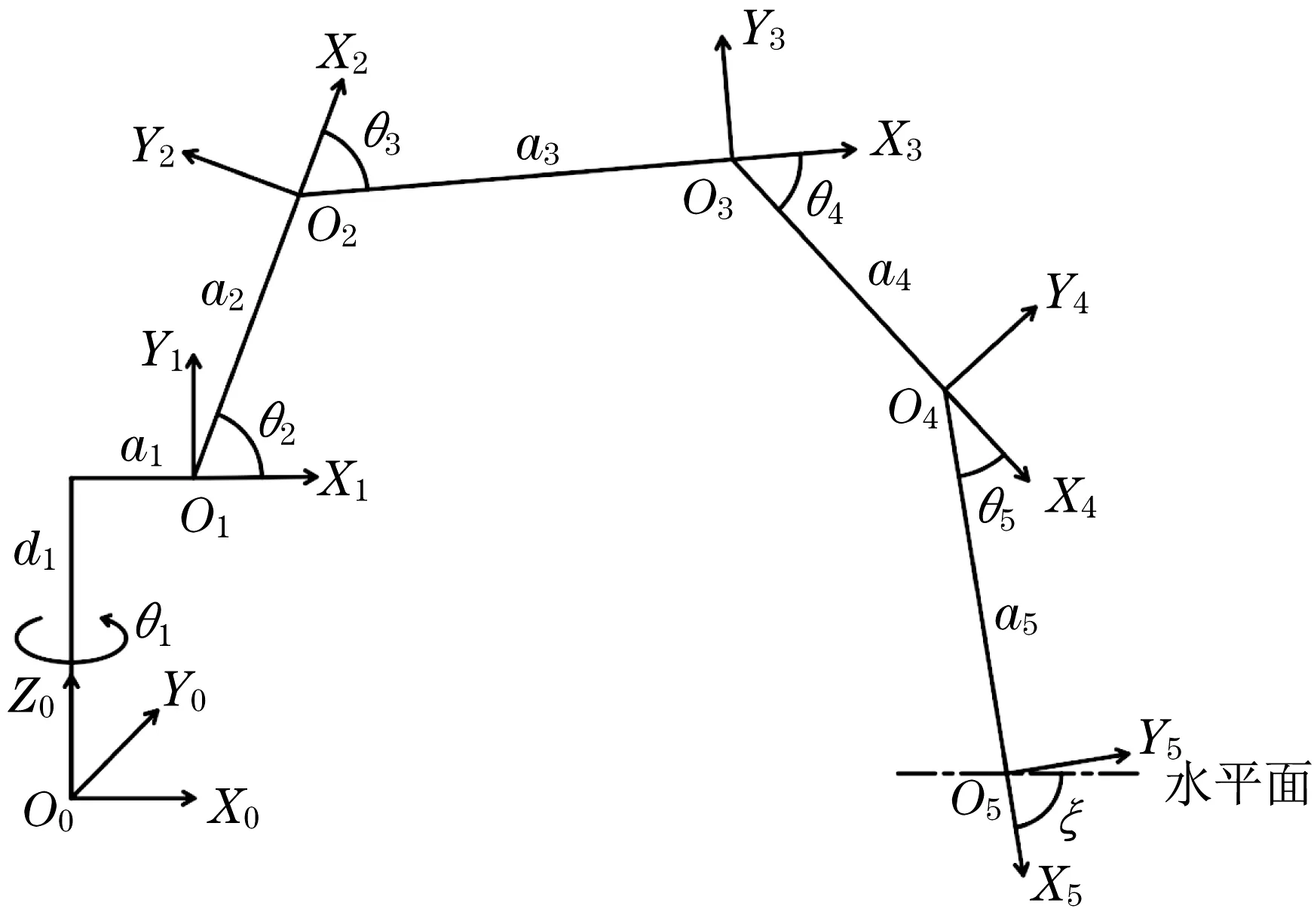
图2 关节坐标系Fig.2 Joint coordinate system diagram
由标准D-H 法的齐次变换矩阵和破拆机器人D-H参数,得到破碎锤锤尖的位姿表达式为
式中:px、py、pz为破碎锤锤尖在基坐标系下的X、Y和Z向坐标;a1、a2、a3、a4和a5为连杆长度;d1为连杆偏移量;ξ为破碎锤锤尖与水平面的夹角;θ1为转台关节角;θ2为大臂关节角;θ3为中臂关节角;θ4为小臂关节角;θ5为破碎锤关节角;c1=cosθ1;c2=cosθ2;c23=cos (θ2+θ3);c234=cos (θ2+θ3+θ4);c2345=cos (θ2+θ3+θ4+θ5);s1=sinθ1;s2=sinθ2;s23=sin (θ2+θ3);s234=sin (θ2+θ3+θ4);s2345=sin (θ2+θ3+θ4+θ5)。
2 破拆机器人拆除窑衬轨迹规划
2.1 拆除窑衬过程分析
根据破拆机器人拆除窑衬的特点,认为需在1个圆环上间隔一定距离和角度进行拆除,因此破碎锤需频繁地转换和定位破拆点。为方便研究,单独分析其中相邻2 个破拆点中的转换路径,假设破碎锤需从破拆点P1定位到相邻破拆点P2。由于在关节空间中进行轨迹规划,并且多关节联动,无法直观地看到在笛卡尔空间的运动轨迹,因此在破拆点转换路径中,预设防撞点D1和D2,使得破碎锤陆续经过防撞点,避免与窑衬发生碰撞,从而将转换路径分为3段轨迹,如图3所示。
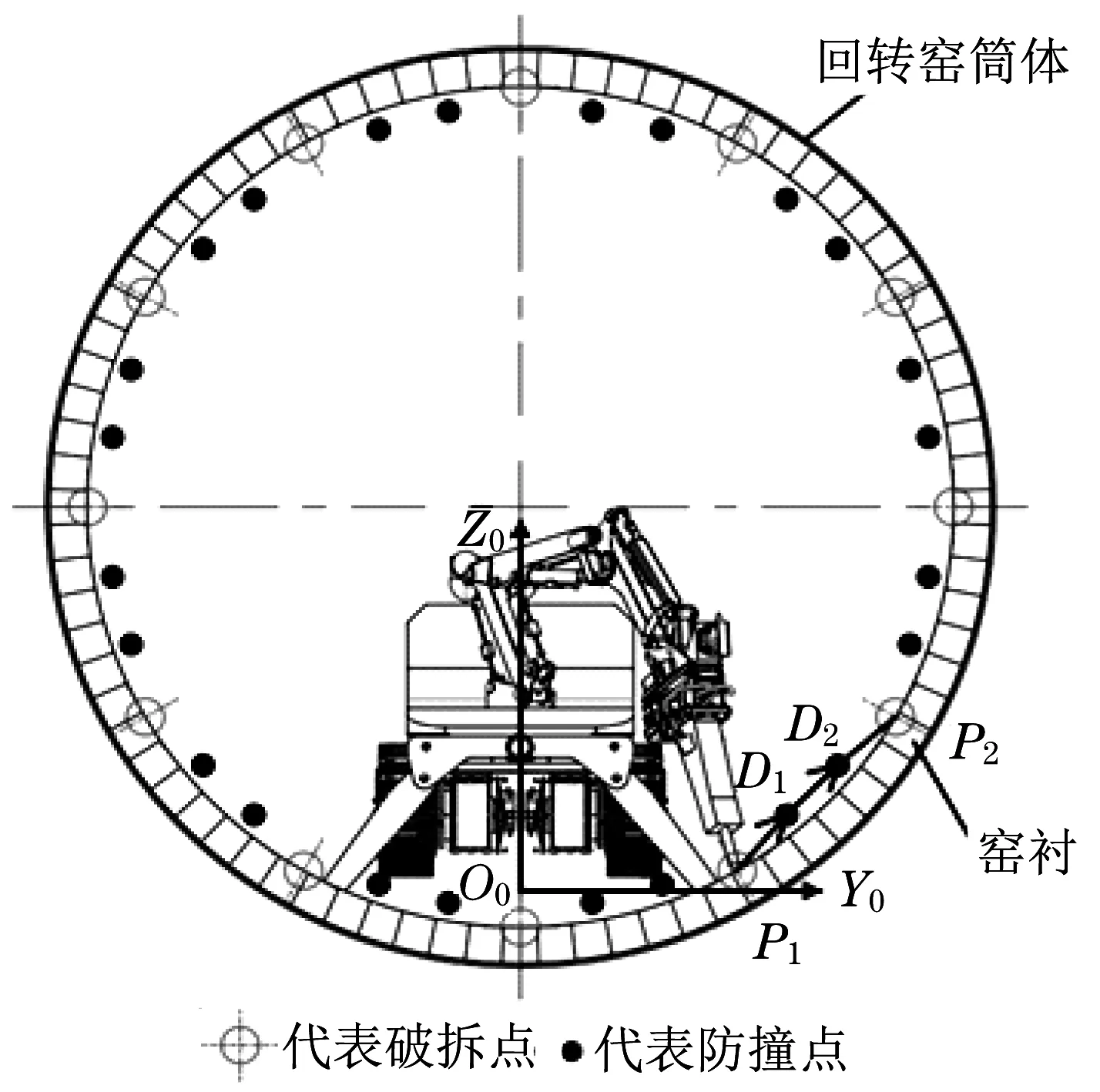
图3 拆除窑衬示意图Fig.3 Schematic diagram of demolish the kiln lining
各关节在破拆点和防撞点的角度见表1。
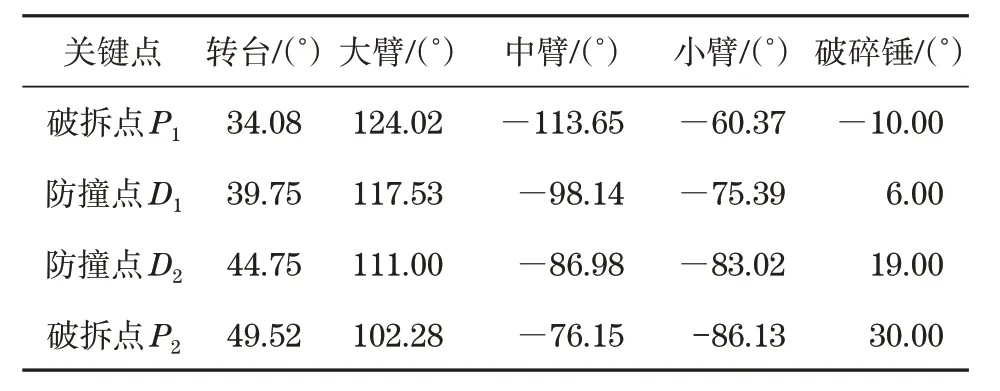
表1 关键点对应关节角度Tab.1 Key points correspond to joint angles
2.2 关节空间的4-3-4多项式插值函数
第i个关节的3段插值函数分别为
式中:θij(t)为破拆机器人第i关节在第j段轨迹内的角度变化;aijk为第i关节在第j段轨迹的第k+1个多项式系数。
破碎锤在破拆点执行拆除任务,各关节在破拆点的角速度和角加速度需为0。此外,各关节在防撞点的角度、角速度和角加速度均需连续。可得约束方程为
式中:Xi0、Xi1、Xi2和Xi3分别表示第i关节在破拆点P1、防撞点D1、防撞点D2和破拆点P2的角度;vi1和vi2分别为第i关节在防撞点D1和D2的角速度;ai1和ai2分别为第i关节在防撞点D1和D2的角加速度;ti1、ti2、ti3为第i关节在第1、2和3段轨迹内所用的时间。
式(3)改写为矩阵的形式为
矩阵的表达式为
根据式(4)~式(7),可求得4-3-4 多项式的系数表达式。
2.3 优化目标和约束条件
优化目标是破拆点转换路径中3 段轨迹的使用时间最少,第i关节的优化目标函数为
运动学约束条件为
式中:Vij、Aij为第i个关节在第j段轨迹的角速度变化和角加速度变化;vimax、aimax为第i个关节的最大角速度和最大角加速度。
各关节角速度和角加速度约束见表2。

表2 各关节角速度和角加速度约束Tab.2 Angular velocity and angular acceleration constraints for each joint
3 改进鲸鱼优化算法描述
3.1 标准鲸鱼优化算法
鲸鱼优化算法是2016 年由Mirjalili 等[7-8]提出的一种群体智能优化算法,分为围着猎物、气泡网攻击和探索猎物3种阶段。
(1) 围着猎物。
座头鲸群体会先假定1 个最优位置,其他座头鲸以最优位置更新自己的位置,表达式如下:
式中:D为鲸鱼个体与最优位置的距离;X*(t)为最优位置;X(t)为当前位置;X(t+1)为更新后的位置;r为[0,1]的随机数。
(2) 气泡网攻击。
气泡网攻击有收缩包围和沿着螺旋形路径2种更新方式。鲸鱼个体采用螺旋形路径来更新位置的公式如下:
式中:D'=|X*(t)-X(t)|代表鲸鱼个体与当前最优位置的距离;b为控制螺旋形状的常数,取1;l为[-1,1 ] 内的随机数。
由于座头鲸同时以收缩包围和沿着螺旋形路径围绕猎物游动,采用概率p确定下一代更新位置的方式,公式如下:
式中:p为[0,1 ] 内的随机数。
(3) 探索猎物。
当|A|≥1 时,鲸鱼个体通过随机选择其他个体位置来更新自己的位置,公式如下:
式中:Xrand(t)为当前随机选择的其他个体位置。
3.2 改进方法
(1) 混沌映射。
标准鲸鱼优化算法通常是随机初始化鲸鱼种群,种群多样性低。混沌具有随机性和遍历性,采用Logistic混沌映射初始化种群[9],公式如下:
式中:Xk为第k个鲸鱼位置的逻辑混沌值;X0∈(0,1),X0∉{0.0,0.25,0.5,0.75,1 .0} ,η=4。
(2) 非线性收敛因子。
鲸鱼优化算法通过收敛因子a控制参数A的变化,进而调整搜索区域[10]。对a采用非线性策略,使得a在搜索前期速度下降明显,加强全局的搜索能力;a在搜索后期的下降速度逐渐变缓,增强局部的搜索能力。公式如下:
式中:t为当前迭代次数;tmax为最大迭代次数。
改进鲸鱼优化算法优化运动时间流程如图4所示。

图4 优化流程Fig.4 Optimization flowchart
4 时间最优轨迹规划仿真
设置鲸鱼种群数量为50,种群维度为3,最大迭代次数为100。用改进鲸鱼优化算法迭代得到转台关节在每段轨迹上的插值时间,如图5所示。改进鲸鱼优化算法对每个关节优化后的插值时间见表3。

表3 每个关节优化后的插值时间Tab.3 Optimized interpolation time for each joint

图5 转台关节插值时间迭代Fig.5 Rotary joint interpolation time iteration diagram
为保证每个关节能够同步运行,不发生碰撞,将每段轨迹的最大时间值作为最终插值时间,可得改进鲸鱼优化算法优化后的总时间为5.882 5 s,未优化前所用总插值时间为7.500 0 s,改进鲸鱼优化算法优化后的总时间比未优化前节省1.617 5 s。
将最终插值时间代入4-3-4 多项式的系数表达式中,得到各关节的位置、角速度和角加速度曲线,如图6~图8 所示。由图可知,优化后的关节位置、角速度和角加速度均连续,且未出现突变,各关节的初末角速度和角加速度均为0。此外,各关节的角速度和角加速度均在运动学约束条件以内,可较好地发挥破拆机器人的运动学性能。
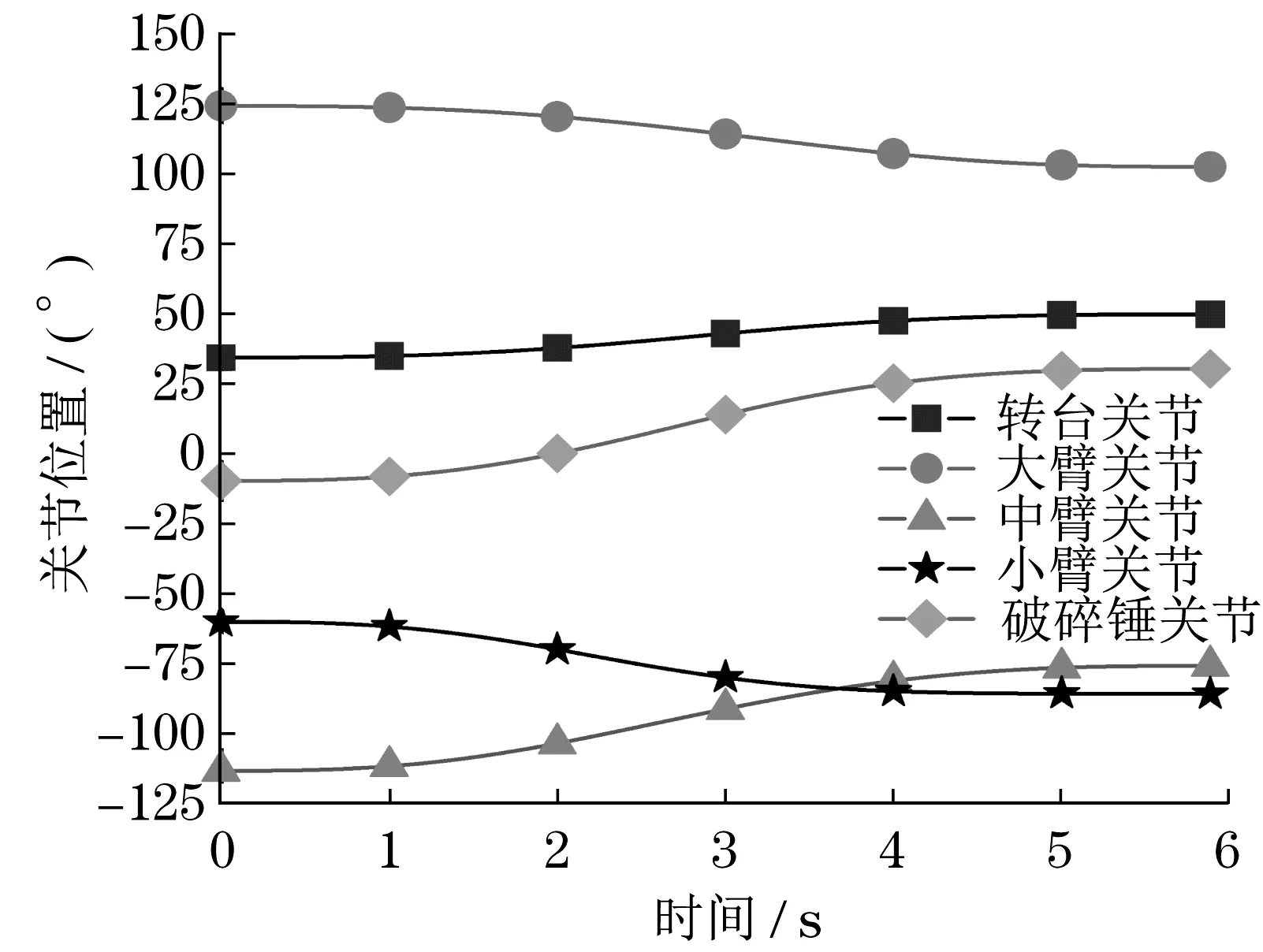
图6 各关节位置曲线Fig.6 The position curve of each joint

图7 各关节角速度曲线Fig.7 Angular velocity curve of each joint

图8 各关节角加速度曲线Fig.8 Angular acceleration curve of each joint
5 结语
本文以破拆机器人拆除窑衬为研究对象,采用4-3-4 多项式插值法在关节空间进行轨迹规划,在满足运动学约束条件下,以运动时间最短为优化目标,采用改进鲸鱼优化算法优化插值时间,运动时间从7.500 0 s 减少到5.882 5 s,提高了破拆机器人的工作效率。
