基于APDL及粒子群优化算法的摩天轮优化设计

黄 游，俞亚新，黄建文，刘云辉

（1.浙江理工大学 机械工程学院，浙江 杭州 310018； 2.浙江巨马游艺机有限公司，浙江 绍兴 312000）

摩天轮主要由支撑系统、轮盘、驱动系统等组成，由于结构和载荷形式十分复杂，目前对摩天轮设计常采用有限元技术进行分析，主要集中在摩天轮重要构件的分析和优化、各荷载对摩天轮的影响。杨蕾璟等［2］采用力学理论，对摩天轮主轴弯曲切应力和弯曲正应力进行公式推导，结合Workbench 对摩天轮主轴进行有限元仿真分析，并研究摩天轮主轴力学特性和安全性。徐伟等［3］对摩天轮在积雪载荷下的空载工况和偏载工况，以及摩天轮在积雪融化后的裹冰荷载下满载运行工况展开分析，通过分析得出摩天轮在积雪和裹冰情况下可安全运行。赵九峰［3］通过对摩天轮进行模态分析得出摩天轮的动力特性，通过振型分解响应谱法，从不同方向计算摩天轮的地震响应，可得水平地震对摩天轮的影响最大。有限元分析软件ANSYS 的参数化设计语言（ANSYS parameter design language，APDL），可对结构进行参数化设计。张滕［4］基于APDL语言建立摩天轮有限元分析模型，分析静力学、动力学和重要零部件。APDL参数化设计语言可以为摩天轮的设计带来便利，但要求设计者熟练掌握ANSYS 的命令。随着摩天轮建造高度的增加，为尽量节约材料，对摩天轮进行整体优化设计具有重要意义。张琦等［5］通过导重法对摩天轮进行轻量化设计。

粒子群优化［6］（particle swarm optimization，PSO）因具有参数少、易理解、易实现等特点，在结构设计中得到广泛关注。郭娟［7］针对双臂机器人末端执行器运行轨迹协调能力差的问题，基于粒子群算法对其优化，优化后的双臂机器人末端执行器精度更高，且协调轨迹能够克服机器人动力学奇异性问题。白洁等［8］针对发动机气门无凸轮驱动控制进度低问题，基于粒子群算法对其优化，优化后气门较优化前控制升程、速度和加速度最大误差更小，控制效果更好。

本文基于Visual Basic.NET 编程语言、APDL语言及Matlab 平台，结合改进的粒子群算法，开发摩天轮参数化设计系统，通过该系统完成摩天轮的优化设计。

1 摩天轮参数化设计系统

本文建立的摩天轮参数化设计系统是将ANSYS 力学分析能力与Matlab 数据处理能力相结合，使用Visual Basic.Net 语言设计交互性良好的界面。系统逻辑如图1 所示。由图1 可知，用户通过界面进行输入和输出参数，系统通过内部代码调用ANSYS和Matlab完成摩天轮参数化建模和基于粒子群算法的摩天轮优化设计。

图1 系统逻辑示意Fig.1 System logic diagram

2 系统理论基础

2.1 摩天轮结构基本形式

摩天轮通过减速机将高转速电动机滚轴转换为低转速转轴，进而实现转轮低速旋转。摩天轮模型如图2 所示，主要包括大立架、转轮、主轴、吊厢系统、电气系统等部分，其中转轮由外环、内环、斜撑、拉索、吊臂架等组成。转轮内环通过交叉布置的拉索与主轴相连，大立架通过主轴底座与主轴相连，通过底部与基础固定联接，从而有效地承载来自各个方向的载荷。

2.2 摩天轮数学模型

2.2.1 设计变量

摩天轮的大立架、转轮内环及转轮外环均为空间桁架结构，采用型材焊接而成。根据GB/T 8162—2018《结构用无缝钢管》、GB/T3094—2012《冷拔异型钢管》和GB/T 11263—2017《热轧H型钢和剖分T型钢》，建立摩天轮型材常用截面数据库，按截面形状分为以下5种类型，各截面参数如图3所示。

图3 摩天轮常用截面Fig.3 Common cross section of ferris wheel

2.2.2 约束条件

空间构件分析时，摩天轮优化设计的约束条件分为强度约束和变形约束，前者保证摩天轮有足够的承载力，后者保证摩天轮在满载运行工况或极限大风工况下不会产生过大的变形。

应力安全系数表达式如下：

式中：σb为材料破断强度，MPa；σmax为构件最大应力，MPa；[n]为许用应力安全系数。

一般构件的安全系数取3.5，重要构件如主轴等安全系数取5［9］。

变形安全系数表达式如下：

式中：∆μ为最大变形，m；H为结构总高度，m。

满载运行工况中，结构最大变形与高度之比小于1/75［9］，极限大风工况中，结构最大变形与高度之比小于1/400。

2.2.3 适应度函数

在摩天轮优化过程中，以降低摩天轮整体质量为目标，因此适应度函数计算公式如下：

式中：i为结构件序号，i=1，2，…，n；mi为第i个结构件的质量，单位kg。

2.3 粒子群算法的改进

粒子群算法在进化过程中易陷入局部极值，存在早熟收敛或停滞现象［10］。针对粒子群算法的不足，提出改进的粒子群算法（improved particle swarm optimization，IPSO），改进策略分别为混沌初始化、粒子动态等级策略及早熟收敛机制。算法优化流程如图4所示。

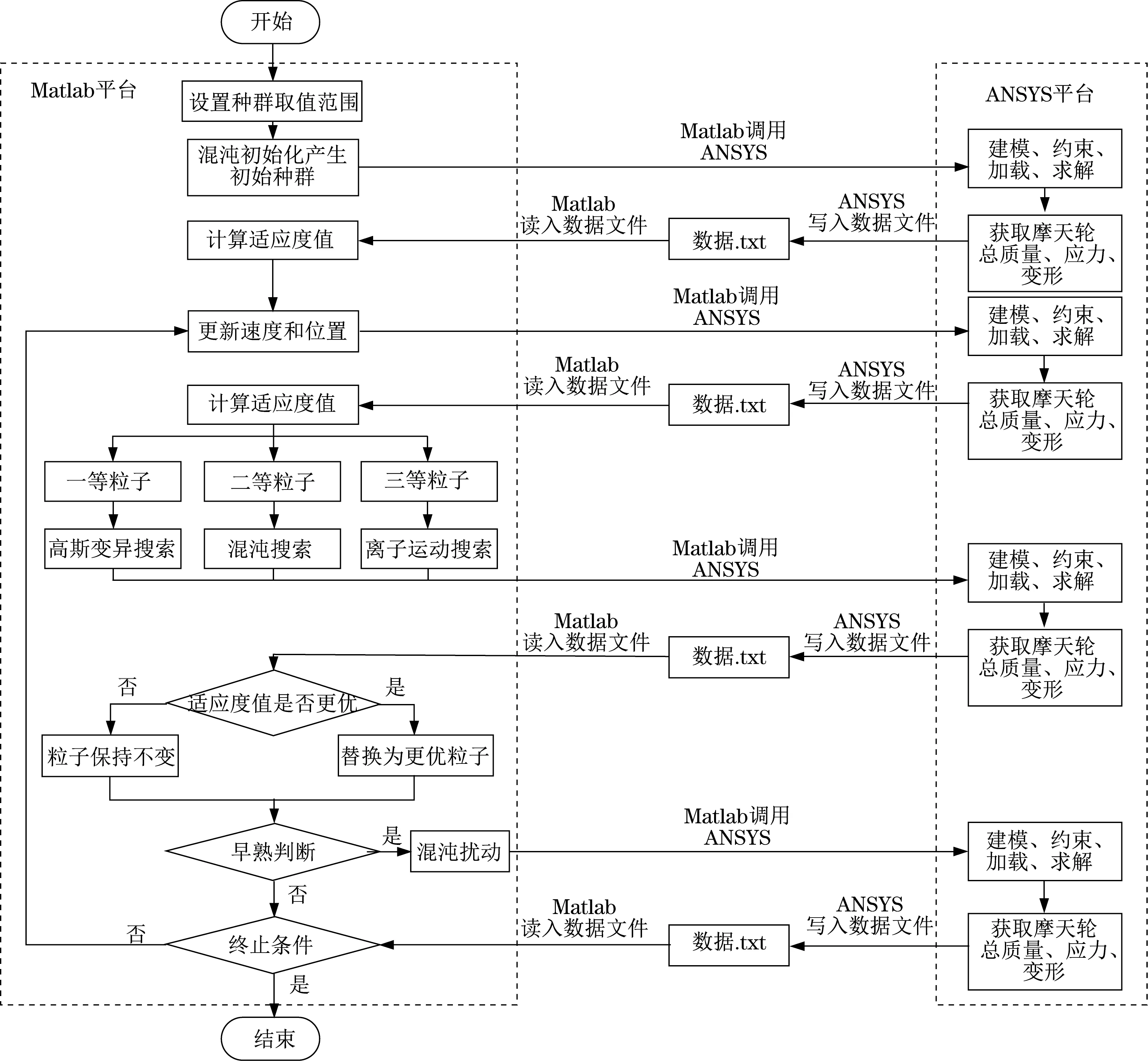
图4 算法优化流程Fig.4 Algorithm optimization flow diagram

2.3.1 混沌初始化

本文采用Tent 混沌映射［11］，利用其遍历性产生均匀分布的混沌序列特点，减少初始值对算法优化的影响，表达式如下：

式中：zi为第i个粒子的混沌序列；，q=4π。

2.3.2 粒子动态等级策略

本文采用一种粒子动态等级策略。迭代过程中，首先根据适应度值计算出个体平均适应度值favg，然后计算优于favg粒子的平均适应度值fa和劣于favg粒子的平均适应度值fb。最后将适应度值优于fa的粒子定义为Ⅰ等粒子，将适应度值劣于fb的粒子定义为Ⅲ等粒子，适应度值介于fa和fb的粒子定义为Ⅱ等粒子。根据不同等级粒子特点，采用不同的搜索策略。

对Ⅰ等粒子采用高斯变异搜索进行局部搜索，公式如下：

式中：N(0，1)为期望为0、标准差为1 的正态分布随机数；为第i个粒子第d维的值；为经过高斯变异后第i个粒子第d维的值。

对Ⅱ等粒子采用混沌搜索，利用混沌映射的随机性和遍历性，增加种群多样性，提高算法的开拓性［11］。

Ⅲ等粒子为当前种群中适应度较差的粒子，距离最优解较远，对Ⅲ等粒子采用离子运动算法（ion motion optimization，IMO）［12］中液体阶段的搜索方式。以全局适应度值最优粒子作为阳离子，Ⅲ等粒子作为阴离子，通过阳离子对阴离子的吸引力，提高Ⅲ等粒子向全局最优解的趋近速度和全局收敛能力。

2.3.3 早熟收敛机制

随着种群的进化，粒子会越来越集中，为防止算法陷入局部最优解，引入早熟收敛机制［13］。当种群粒子个体平均距离l小于临界值λ时，认为算法出现早熟，即l<λ。平均距离l计算公式如下：

式中：N为种群粒子总数；D为粒子维数；xij为第i个粒子第j维的值；xa，j为第j维粒子平均值。

3 优化结果与性能评估

本文以某高为91 m 的摩天轮为例，为体现改进后的粒子群算法的优化性能，选用混沌粒子群算法（chaotic particle swarm optimization，CPSO）、离子运动算法作为对比。各算法相关参数设置见表1。

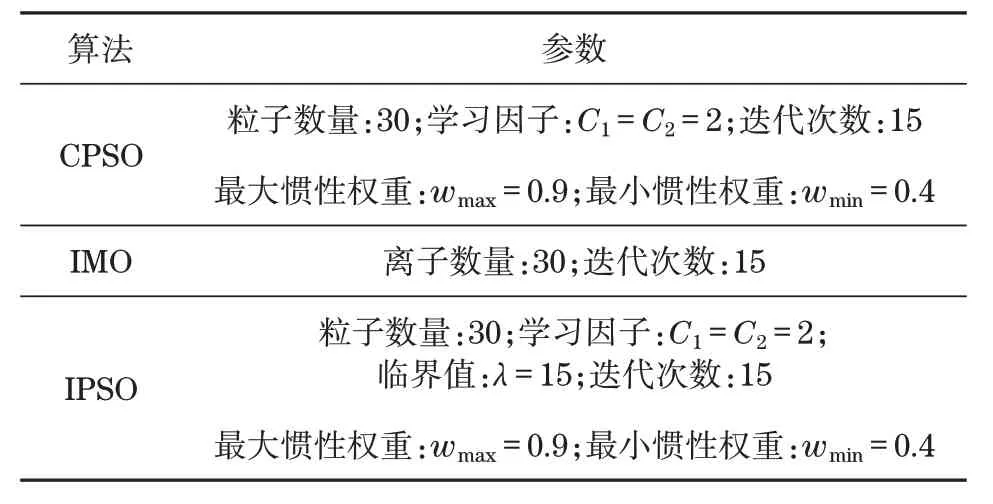
表1 算法相关参数设置Tab.1 Algorithm-related parameter settings

经3 种算法优化后，大立架、转轮内环和转轮外环截面参数见表2。其中，大立架截面和转轮内环截面均为环形截面，转轮外环截面为环形截面与矩形管组合截面；Dc、tc分别为大立架圆环外径和壁厚；Dk、tk分别为转轮内环圆环外径和壁厚；Dr、tr1、Br、Hr和tr2分别为转轮外环圆环外径、圆环壁厚、矩形管外宽、矩形管外高和矩形管壁厚。

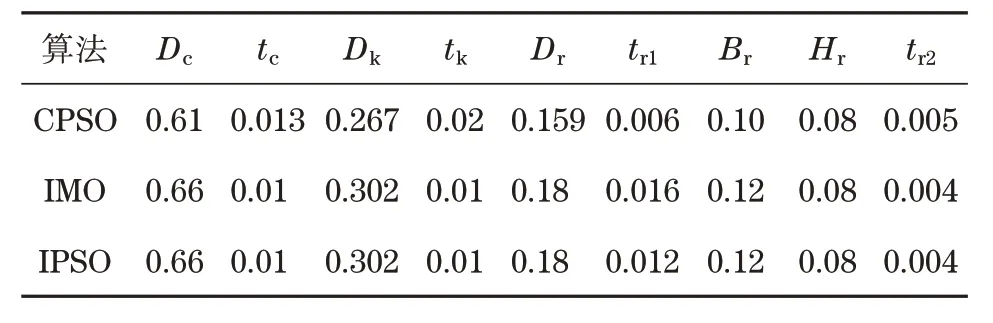
表2 构件截面参数Tab.2 Component section parameters

3 种优化算法模型应力及变形见表3。由表3可知，经算法优化后的摩天轮均达到强度要求和刚度要求，且完成了摩天轮优化设计要求。以大立架为例，CPSO 优化后的大立架安全系数为470/127=3.70，IMO 优化后的大立架安全系数为470/133=3.53，IPSO 优化后大立架安全系数为470/134=3.51。其中IPSO 优化后的大立架安全系数最小，且满足大于许用安全系数3.5的约束条件。因此认为IPSO 算法找到全局最优解，其他2 种算法皆陷入局部最优解。

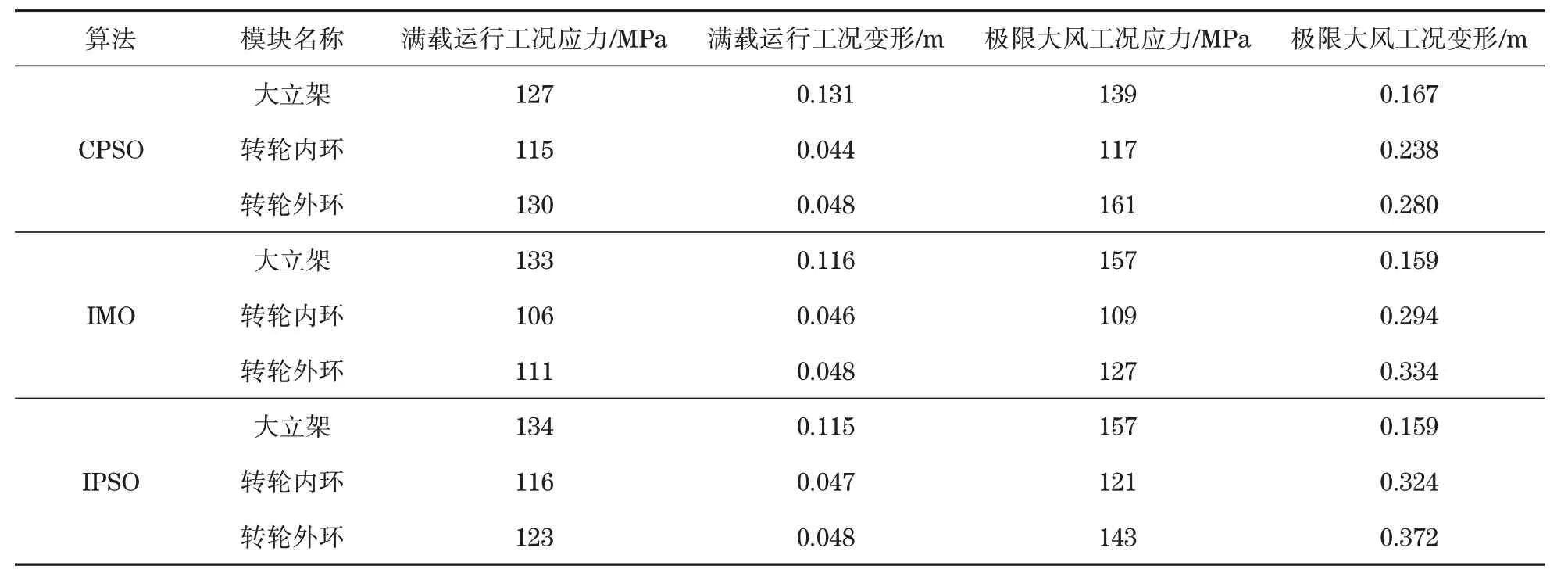
表3 3种优化算法模型应力及变形Tab.3 Three optimization algorithms model stress and deformation

3种优化方法整体质量对比见表4。由表4可知，在3种算法中，IMO优化效果最差，摩天轮整体质量最大，为343 406 kg。CPSO优化效果次之，优化后的摩天轮整体质量为331 252 kg。IPSO优化效果最好，优化后的摩天轮整体质量为321 650 kg，与IMO优化后的摩天轮整体质量相比，减少21 756 kg；与CPSO优化后的摩天轮整体质量相比，减少9 602 kg。

表4 3种优化方法整体质量对比Tab.4 Comparison of the overall quality of the three optimization methods

综上所述，通过摩天轮参数化设计系统可提高摩天轮设计效率，且改进的粒子群算法优化效果明显。在实际的摩天轮设计中，设计者考虑安全裕度，不会采用一般构件应力安全系数接近3.5 的极限值，但通过算法对摩天轮优化设计后的数据可为设计者提供参考。

4 结论

（1） 以摩天轮为研究对象，基于VB.NET编程语言、APDL语言及Matlab平台，编制摩天轮参数化设计系统。利用该系统完成摩天轮的参数化建模、分析及优化，可以缩短设计时间，提高设计效率。

（2） 通过混沌初始化、粒子动态等级策略及早熟收敛机制对粒子群算法提出改进，有效地改善粒子群算法容易陷入局部最优解、早熟收敛等问题，提高了粒子群算法的优化效果和稳定性。

（3） 通过摩天轮参数化设计系统对摩天轮进行优化。优化结果表明，优化后的摩天轮在满足设计要求的条件下，达到优化设计效果，对摩天轮设计具有指导意义。