基于刚柔耦合的机械臂架系统关键焊缝精细化计算与优化

张 鑫，周志红，朱 奇

（湖南工业职业技术学院 机械工程学院，湖南 长沙 410208）

臂架系统是混凝土泵车、挖掘机、登高车、折叠式消防车等诸多工程机械装备中的重要部件［1］。通常由多节单元臂架及连接部件组成，单元臂架一般采用薄壁箱型焊接梁结构，由不同规格的高强度钢板拼装焊接形成，焊缝直接影响设备的使用安全。因此，焊缝的设计计算是臂架系统设计的重要组成部分［2］。对于长度更长、柔性更大、臂节数更多的长臂架系统，其焊缝特别是关键焊缝的计算和校核尤为重要。

刚柔耦合分析是多体动力学与有限元相结合的技术，非常适用于柔性体因素影响较大的臂架系统。对臂架系统进行刚柔耦合分析，不但能得到部件在不同工况下的应力应变，也能得到部件在典型工况下更为真实的铰孔载荷，这些可为部件与局部结构的设计优化提供更加准确的依据［3-5］。

子模型技术是对局部结构进行精确计算的方法，子模型技术既考虑了整体模型中局部结构计算不准确的问题，又考虑了计算资源与计算效率的问题，适合大型构件局部结构的计算［6-8］。

混凝土泵车臂架系统是典型的大柔性、多臂节、多工况部件。本文以一款长臂架混凝土泵车的臂架系统设计为例，基于臂架系统的刚柔耦合特性，以关键焊缝为研究对象，利用子模型技术对焊缝进行精细化计算和评估，提出优化方案，并应用于工程实际。

1 混凝土泵车臂架系统

混凝土泵车臂架系统主要由转台、单元臂架、连杆组、油缸及相关辅件组成，如图1 所示。各节臂从转台开始，分别命名为第1 节臂至第N节臂，臂架之间通过油缸驱动实现臂架系统的不同姿态，以适应不同工况［9-10］。各单元臂架的铰孔，通过销轴分别与前后臂架、连杆及油缸相连接。通常臂架系统中1 节臂、2 节臂、连杆组、油缸等具有较好的刚性，而转台、3 节臂、4 节臂、5 节臂是典型的细长杆、大柔性部件。转台为单板结构，如图2 所示。3节臂是Z 形臂架，如图3 所示，这2 个部件受力复杂，其关键焊缝的设计尤为重要。

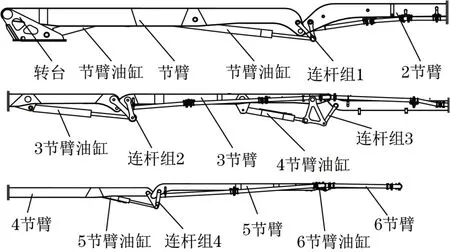
图1 混凝土泵车臂架系统组成Fig.1 Structure of boom system of concrete pump

图2 转台三维模型Fig.2 3D model turret

图3 3节臂三维模型Fig.3 3D model 3rd boom

2 臂架系统关键焊缝设计

某型号长臂架混凝土泵车3 节臂由高强度钢板焊接而成，上、下盖板的对接焊缝是臂架的关键焊缝。上盖板由厚度10 mm 与5 mm 的钢板对接，下盖板由厚度12 mm 与8 mm 的钢板对接，对接边开单面全长度坡口，坡口角度35°，钝边1 mm，焊缝设计成“V”形焊，上、下盖板坡口及焊缝标注如图4所示。焊接时，使用高强度等级焊丝（屈服强度为890 MPa，许用应力为530 MPa），采用单面焊双面成型工艺。

图4 3节臂上、下盖板对接坡口尺寸与焊缝标注Fig.4 Dimensions of butt groove and weld marking of the upper and lower cover plates

转台使用的钢板材料、焊丝与臂架相同，底板、左右立板、围板和连接板的钢板厚度分别为55、40、12 和10 mm。立板与底板相交处的焊缝是转台的主焊缝，也是关键焊缝。立板下端开双面全长度坡口，坡口角度35°，长度19 mm，立板下端坡口尺寸如图5 所示。焊缝设计成坡口焊加角焊，焊高20 mm，焊缝标注如图5 所示。焊接时双面连续、对称施焊。

图5 转台立板坡口尺寸与焊缝标注Fig.5 Dimensions of groove and weld marking of the turret vertical plate

为校核3 节臂与转台关键焊缝的强度，优化焊缝参数，本文基于臂架系统刚柔耦合特性，利用子模型技术，对关键焊缝进行精细化计算与优化。

3 臂架系统刚柔耦合动力学分析

将混凝土泵车臂架系统中的转台与3、4、5 节臂视为柔性体，在ANSYS Workbench 中建立整个臂架系统的刚柔耦合模型，并进行动态仿真分析。臂架系统刚柔耦合分析中水平工况下的整体应力与变形云图如图6 所示。由图6 可知，臂架系统整体应力分布与变形较合理，臂架系统刚柔耦合模型具有较好的可信度。臂架系统在施工过程中有无数种姿态，部件与局部结构计算时，一般选取典型工况作为计算工况。

图6 水平工况下臂架系统整体应力与变形云图Fig.6 Overall stress and deformation cloud diagram of boom system under horizontal working condition

3.1 转台动力学仿真分析

转台的危险工况是1 节臂在油缸作用下由水平至竖直状态运动，其他臂架始终保持水平。转台上、下铰孔在危险工况过程中的载荷变化曲线如图7所示。由图7可知，转台2个铰孔的载荷均出现不同程度的波动，1节臂接近竖直的状态下，铰孔载荷出现较大范围的波动，说明柔性体因素对载荷振动性的影响，与臂架系统在实际工作过程中的振颤现象较为相符。转台典型计算工况为臂架系统水平工况，从载荷曲线中分别提取转台上、下铰孔载荷，见表1，表中FX为轴向载荷，FY为径向载荷，∑F为当量载荷。

表1 水平工况下转台上、下铰孔载荷Tab.1 Load on upper and lower holes of the turret under horizontal working condition

图7 转台铰孔载荷变化曲线Fig.7 Load variation curve on the hole of the turret

3.2 3节臂动力学仿真分析

3 节臂的危险工况是4、5 和6 节臂始终保持水平并在0°~135°的范围内运动。3 节臂的典型计算工况为水平、油缸力最大和转角最大3 个工况，臂架姿态示意如图8 所示。在载荷曲线中分别提取3种典型工况下各铰孔的载荷数据，见表2~表4。由表可知，A为3臂与2臂铰孔，B为3臂与连杆组2铰孔，C为3臂与油缸铰孔，D为3臂与连杆组3铰孔，E为3臂与4臂铰孔。注：FX为轴向载荷；FY为径向载荷；∑F为当量载荷。

表2 水平工况下3节臂各铰孔载荷Tab.2 Load of upper and lower holes of the 3rd boom under horizontal working condition

表3 最大转角工况下3节臂各铰孔载荷Tab.3 Load on each hole of the 3rd boom under the max angle condition

表4 油缸力最大工况下3节臂各铰孔载荷Tab.4 Load on each hole of the 3rd boom under the condition of max cylinder force

图8 3节臂计算工况Fig.8 Calculation working condition of the 3rd boom

通过臂架系统的刚柔耦合动力学分析，获得转台与3 节臂在典型工况下的初步应力结果和铰孔载荷，为关键焊缝的精细化计算奠定了基础。

4 臂架系统关键焊缝精细化计算

4.1 3节臂与转台整体结构应力分析

利用子模型技术对焊缝进行精细化计算，对部件展开整体结构应力分析。分别计算3节臂在3种工况下的整体应力，对比应力云图发现，3 节臂上、下盖板对接处应力在水平工况下最大，应力云图如图9 所示。由图9 可知，上盖板对接处大部分区域的应力已接近许用应力。同样计算转台在水平工况下的应力，得到整体应力云图，如图10 所示。由图10 可知，转台立板与底板相交处大部分区域应力较低，立板工艺孔处最大应力为612.3 MPa，范围较小且未超出材料屈服强度。为获得3 节臂与转台关键焊缝更精确的应力分布，建立焊缝模型，并对焊缝进行二次应力分析。

图9 3节臂整体及对接处应力云图Fig.9 Stress cloud diagram of the whole and joint of the 3rd boom

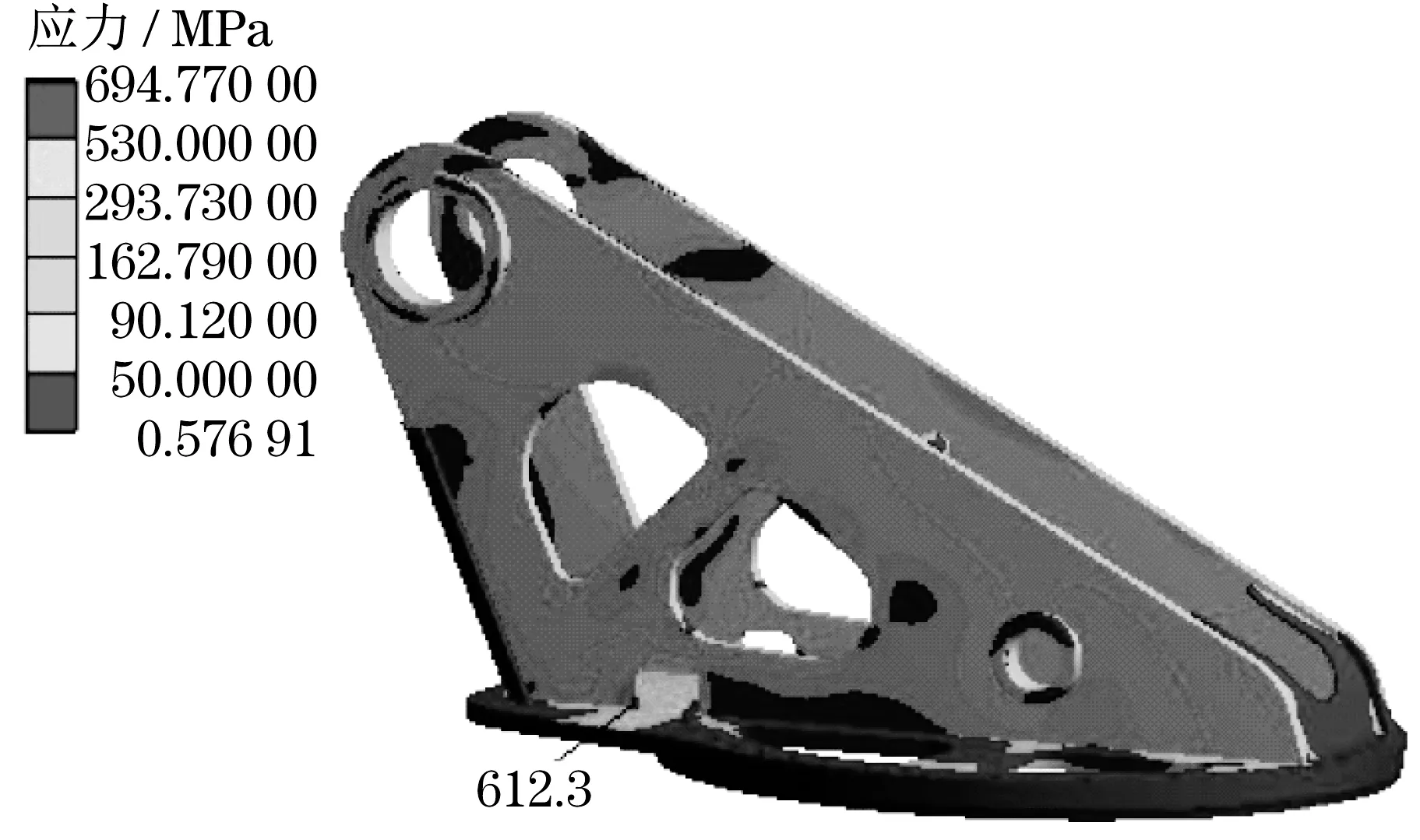
图10 转台整体应力云图Fig.10 Overall stress cloud diagram of the turret

4.2 焊缝子模型计算

在3 节臂上、下盖板对接处及转台立板与底板交接处距离焊缝合适的位置截取模型，按照实际参数建立焊缝模型，将整体模型切割边界上的位移值作为边界条件，并施加在截取的模型上，得到3 节臂上、下盖板对接焊缝与转台主焊缝的子模型。为验证计算结果的收敛性和可靠性，对子模型进行逐步网格细化计算。不同网格划分方式下计算得到的焊缝最大应力值变化曲线如图11 所示。由图11可知，随着网格细化，焊缝区域的最大等效应力逐渐收敛。由图12 和图13 可知，子模型焊缝区域最大应力比整体模型计算时的应力明显偏大，3 节臂上盖板对接焊缝最大应力已超过材料的许用应力且范围较大；与整体计算时的最大应力相比，转台立板工艺孔焊缝处应力明显偏大，但分布范围较小，小于材料的屈服强度。

图11 子模型焊缝最大应力变化曲线Fig.11 Max stress variation curve of welding of the sub model

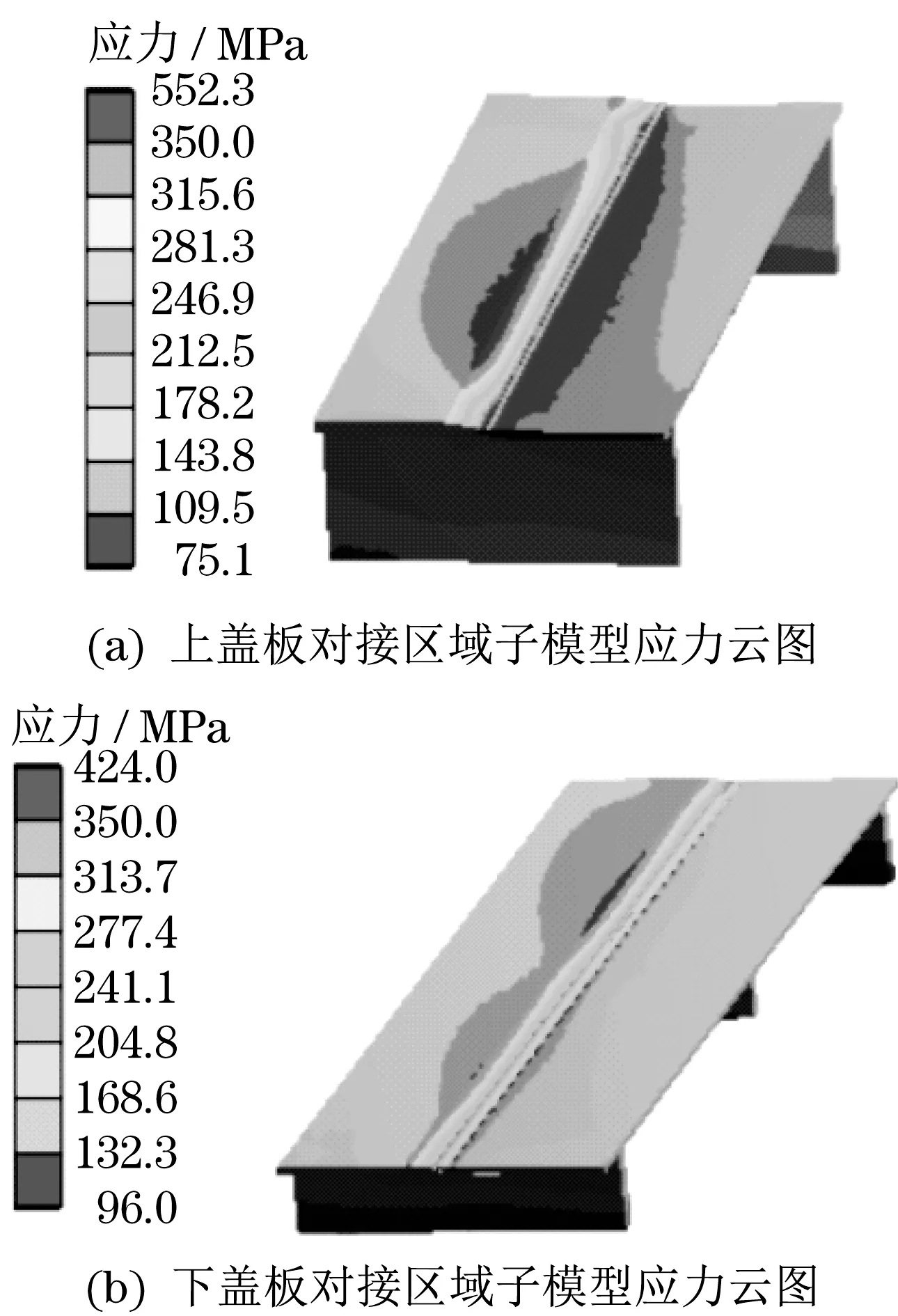
图12 3节臂上、下盖板对接区域子模型应力云图Fig.12 Stress nephogram of the sub-model of the joint area of the upper and lower cover plates of 3rd boom

图13 转台主焊缝区域子模型应力云图Fig.13 Stress nephogram of the sub-model of the key weld area of turret

4.3 焊缝子模型边界验证

为验证子模型切分方法的可信度，对模型的切割边界进行验证，在整体模型和子模型中，分别创建切割面路径，获取沿路径的应力分布并进行对比。3 节臂与转台整体模型、子模型切割面路径应力分布对比曲线如图14 和图15 所示。由图14和图15 可知，子模型与整体模型在切割面上的应力分布基本一致，因此切分方法具有较高的可信度。

图14 3节臂切割面路径应力对比曲线Fig.14 Comparison curves of path stress on the cutting surface of the 3rd boom

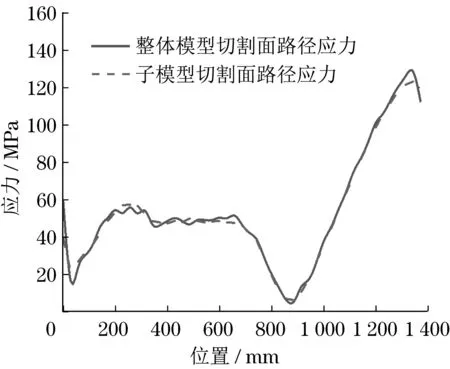
图15 转台切割面路径应力对比曲线Fig.15 Comparison curves of path stress on the cutting surface of the turret

5 臂架系统关键焊缝优化设计

5.1 3节臂对接焊缝优化设计

由3 节臂子模型计算结果可知，需适当降低上盖板对接焊缝应力值。将对接钢板坡口由35°改为45°，计算后发现焊缝应力值有所降低但不明显，且增大坡口角度将增加机加与焊接工作量，因此不宜调整坡口角度。根据臂架整体应力分布，将上盖板对接焊缝后移400 mm，下盖板对接焊缝前移200 mm。计算上盖板焊缝最大应力为431 MPa，与优化前相比有明显降低，且高应力区大大减少；下盖板焊缝最大应力为447 MPa，与优化前相比变化不大。上、下盖板焊缝位置调整后，对接焊缝应力满足要求且臂架整体重量几乎没有增加。

5.2 转台主焊缝优化设计

转台主焊缝共4 条，每条焊缝长度在1.5 m 以上，焊缝由坡口焊和角焊组成，焊接工作量与焊接变形较大。由转台子模型分析结果可知，转台主焊缝虽然满足强度要求，但如果进一步优化主焊缝参数对生产将具有重要意义。目前主焊缝焊高为20.0 mm，实际的最低焊高要求为13.3 mm（实际产品中最低焊缝高度须高于焊缝坡口角度为35°、宽度为19 mm 的对边高度），将焊高调整为15.0 mm，计算后发现主焊缝应力值为758 MPa，满足强度要求，且可减少焊接工作量。

6 结论

本文以某型号长臂架混凝土泵车臂架系统的关键焊缝为研究对象，基于刚柔耦合特性，采用子模型技术对焊缝进行精细化计算与优化，得出以下结论。

（1） 通过大柔性、多臂节机械臂架系统的刚柔耦合动力学分析，不仅可得到部件的初步计算结果，还可获得臂架系统不同工况下铰孔的真实载荷，为部件与局部结构的精确计算奠定基础。

（2） 使用子模型技术对臂架系统关键焊缝进行精细化计算，可得到焊缝更加真实的应力分布，为焊缝强度的评估与优化提供依据。

（3） 本文的分析方法可为大型构件局部结构的设计提供参考。