在数学活动课中促进学生高阶思维能力发展

[摘  要] 文章从以下三个方面阐述在数学活动课中如何促进学生高阶思维能力发展：把培养学生高阶思维能力作为数学课堂教学的价值追求;创设合适的情境，唤醒学生的数学意识;精心设计问题，让数学活动植入理性思维.

[关键词] 数学活动课;高阶思维能力

作者简介：陈颍（1984—），本科学历，中学一级教师，从事初高中数学教法和学法的研究工作，曾获广州市优秀教师称号，广东省首届中小学青年教师教学能力大赛一等奖，广州市第六届初中数学十佳青年教师，广州市中小学数学骨干教师.

高阶思维是指发生在较高认知水平层次上的心智活动或认知能力[1]. 数学是思维的体操，思维是数学的心脏，培养学生高阶思维能力需要串联的高阶数学学习活动予以支撑，而数学活动课则是一个有效的载体. 本文以人教版数学七年级上册第二章“整式的加减”中的数学活动为例，谈谈数学活动课中如何促进学生高阶思维能力的发展.

教学实践过程

1. 教学环节1：创设情境，初探规律

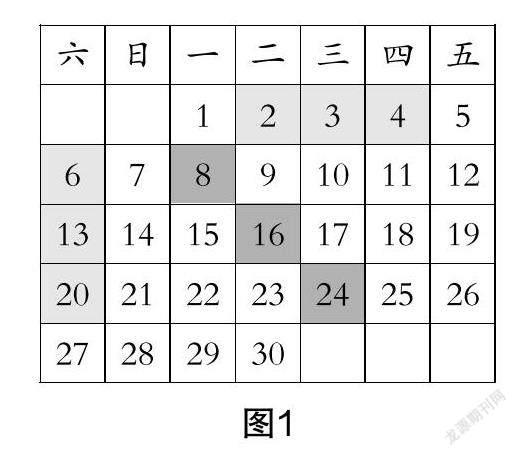
师：今天我们先玩一个“猜和”游戏，需要几组同学配合完成. 同学A出题，同学B答题. 游戏规则是：如图1所示，同学A框出某月的月历中任意形式连续的三个数，求和后告诉同学B;同学B在3秒内说出这三个日期.

（学生踊跃参与，学生A分别从横、竖、斜三个不同的角度提问）

师：大家是如何得到这三个日期的？

生1：把它们的和除以3可以得到中间的日期.

师：你是怎么发现的？

生1：月历中三个连续的数的排列有规律，横的差1，竖的差7，左斜差6，右斜差8，首尾两个数与中间的数的差正好抵消了.

师：很好！我们怎么用数学的方法表示这种规律？以横排差1的为例.

生2：可以设中间的数为a，前面一个数为a-1，后面一个数为a+1，三个数的和为3a，即中间数的3倍.

生3：也可以设第一个数为a，则中间的数为 a+1， 第三个数为a+2，三个数的和为3a+3=3（a+1），也是中间数的3倍.

生4：还可以设第三个数为a，则第一个数为 a-2， 中间的数为a-1，三个数的和为3a-3=3（a-1），也是中间数的3倍.

教师板书以上三种表示方式进行对比：

师：三种表示方式不同但都是正确的，大家觉得哪种方式更好？

生5：第一种！因为关系最简洁明显，计算也最简便.

师：这个结论对任何一个月历都成立吗？为什么？

生6：都成立，因为字母a可以表示月历中的任何一个数.

师：是的，这就是用字母表示数并进行推理的好处，更具有一般性.

教学分析 高阶思维的产生源于学生的求知欲，教师通过游戏创设情境，能激发学生的好奇心，引导学生观察发现规律，会用字母表示数来证明规律.

2. 教学环节2：合作交流，规律再探

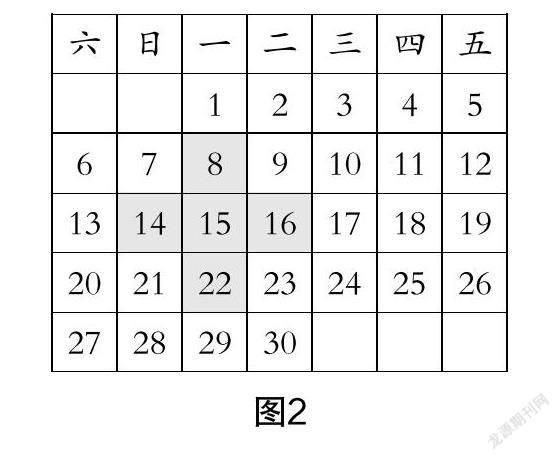
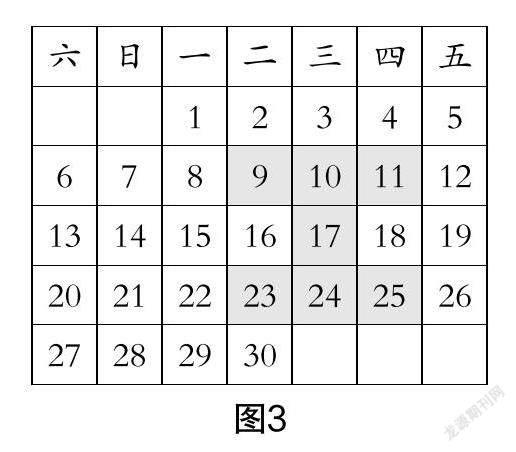
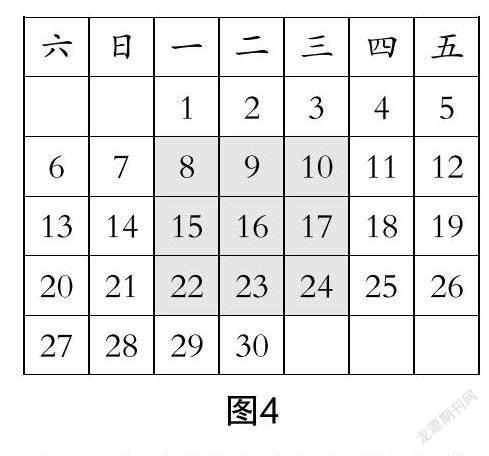
师：我们发现了三个相邻日期的规律，如图2、图3、图4所示，如果方框变为十字形（5个数）、工字形（7个数）、“3×3”九宫格（9个数），方框中所有数的和是多少呢？怎样运算简便？

生7：十字形方框中所有数的和是正中心数的5倍，工字形方框中所有数的和是正中心数的7倍，“3×3”九宫格中所有数的和是正中心数的9倍.

师：你是怎么得到这个关系的？如果移动方框，这个结论是否依然成立？

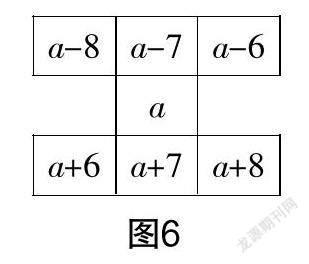
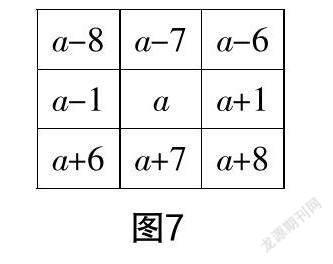
生7：与前面的方法类似，设正中心数为 a，其他数全部可以用a表示出来，所有数的和也可以用a表示出来（如图5、图6、图7所示，教师投影学生画的图），求和时常数项部分全部抵消了，只剩下含字母a的了，就可以得到十字形5个数之和是5a，工字形7个数之和是7a ，“3×3”九宫格9个数之和是9a.

师：不错，你运用类比的方法发现了一般性结论.

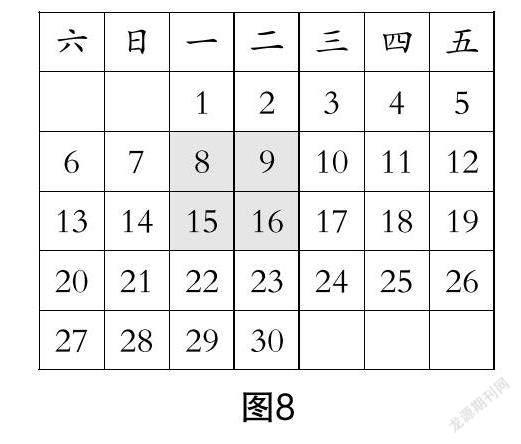
师：接下来，我们继续改变方框的形状，如果方框变化为“2×2”正方形呢？（如图8所示）

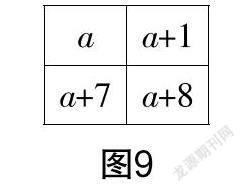
生8：对角线数之和相等， 即a+（a+8）=（a+1）+（a+7），如图9所示.

生9：所有数之和为a+a+1+ a+7+a+8=4a+16=4（a+4），和为4的倍数，但是和并不是其中任何数的4倍.

生10：老师，我还发现（a+1）（a+7）-a（a+8）=7，也就是对角线两个数乘积的差都等于7.

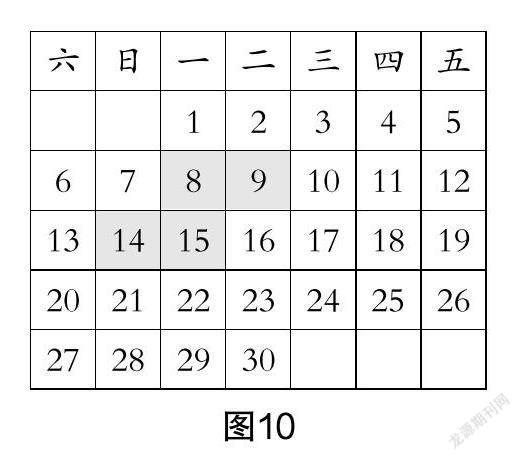
师：你们能从不同的角度去看问题，非常好！若再改变一下方框的形状，如图10所示，又会有哪些结论？

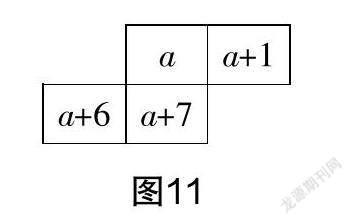
生11：还有对角线数之和相等，即a+（a+7）=（a+1）+（a+6），如图11所示.

生12：对角线两个数乘积的差都等于6， 即（a+1）（a+6）-a（a+7）=6.

生13：但是它们的和为4a+14， 不是4的倍数.

师：确实！类比前面的思考，发现结论是不一样的.

教学分析 方框形狀的变化，方框里的日期从奇数个变化到偶数个，体现了认知过程和认知方法的系统性与连贯性，以及用字母来推理的理性思维，是发展符号意识、抽象素养和数学建模的过程. 结论不是唯一的，能发散学生的思维，引导学生关注问题本身，关注问题提出和解决的过程，关注思维的方式方法，从而提升高阶思维能力.

3. 教学环节3：发散思维，举一反三

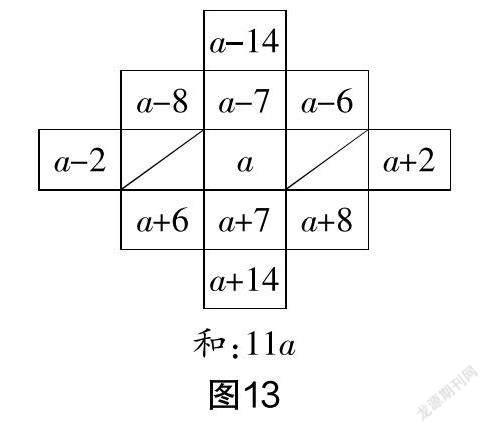
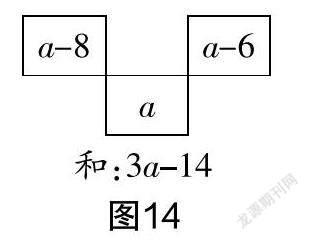
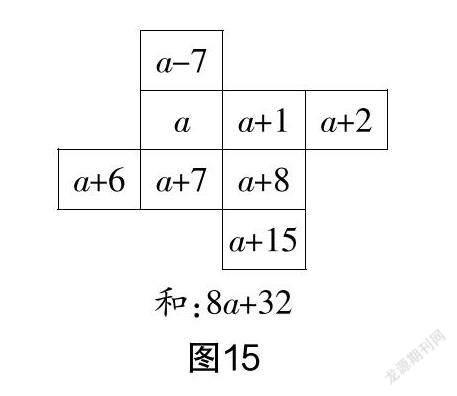
师：以月历为背景，请你设计一个与之前形状不同的阴影方框，尝试发现其中的规律. （图12、图13、图14、图15是部分学生给出的设计和结论）

师：大家给出了各种各样的设计，我们来对比一下，思考：为什么有的设计的结论很简洁，数的关系也很直观，而有的设计的结论并不是那么简洁和直观？为什么有些规律是延续的，有些规律不是延续的？这与什么有关呢？

生14：与设计的方框的对称性有关.

生15：具有中心对称的方框中所有数的和等于中心數乘数的个数，并且只有奇数个才成立.

师：不错，在中心对称的前提下，我们体会了背景变化下规律的不变性.

教学分析 条件和结论双开放性探究，能使学生发散思维，有助于学生创新思维的发展. 此环节给了学生一个足够的思维空间，让学生在自主参与、动手实践、展示设计、表达交流中生长思维. 有些学生设计的方框中的规律并不明了，教师应引导学生进一步思考其内在联系，即结论的简洁性与方框的对称性的关系.

4. 教学环节4：经验内化，拓展迁移

问题：所示的数阵全部由偶数排成.

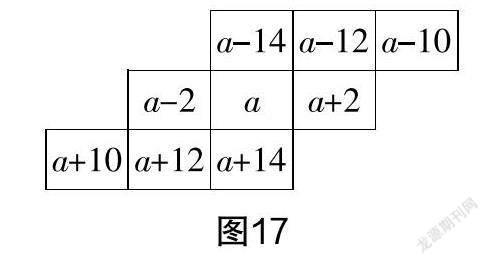
（1）如图16所示，用一个平行四边形任意框出9个数， 这9个数之和能等于1017吗？1980呢？2016呢？若能，请写出这9个数中最小的数;若不能，请说明理由.

生16：设中心数为a，则平行四边形框内的数都可以用a表示，如图17所示. 9个数之和为9a，令9a=1017，则a=113，因为a是偶数，所以9个数之和不可能等于1017;同理，令9a=1980，则a=220，所以最小的数是206;令9a=2016，则a=224，所以最小的数是210.

师：转化成一元一次方程来解决，很好！大家有没有不同的想法？这个过程有没有问题？

（基于前面解决问题的经验，大部分学生都同意生16的想法）

师（追问）：题目问某数是否存在，是一个存在性问题，大家试一试在数阵中找找数的位置.

（学生又投入到了思考当中，数分钟后）

生17：老师，我发现a=220是数阵中的第110个偶数，数阵每一行有7个数，110÷7=15……5，因此220在数阵中是第16行从左到右的第5个数，是存在的;但是a=224是数阵中的第112个偶数，在数阵中是第16行从左到右的最后一个数，这样的平行四边形框是不存在的，所以这9个数之和不可能等于2016.

（教师板书过程，学生通过仔细聆听有所顿悟）

师：嗯，这个补充使整个解答过程更完美，平时学习中我们既要捕捉关键的信息，还要注意严谨性.

（2）如图18所示，用“4×4”方框任意框出16个数，它们的和等于1120是否可能？若能，请写出这16个数中最小的一个数;若不能，请说出理由.

（由于时间原因，第（2）个小问留给学生课后思考）

教学分析 这类问题可以分解为多个小问题：用字母表示数分析规律，利用一元一次方程解决存在性问题. 此环节中，学生不仅要类比迁移探究方法和过程，而且要通过“是否存在这样的数”把解方程的结果回引到数阵中进行检验. 通过问题解决，深化建模思想，学生能做到融会贯通这种高阶思维发展的表征.

5. 梳理回顾，提升认识

月历→数→字母表示数→代数式运算探索、证明规律→研究一般数阵.

数学知识：整式的加减，一元一次方程.

数学思想：从特殊到一般，转化与化归，数学建模，方程思想.

教学分析 引导学生提炼知识和方法，体会数学思想，将感性认识提升为理性认识.

数学活动课中促进学生高阶思维能力发展的教学思考

1. 把培养学生高阶思维能力作为数学课堂教学的价值追求

作为教师，先要明确日常课堂教学是培养学生高阶思维的主阵地，把培养学生高阶思维能力作为教学的价值追求. 所以备课时，教师要在理解教材的前提下对教材内容进行整合和深化，要设计层层递进的环节引领学生深入思考，不仅让学生掌握通性通法，还要看到问题的本质. 本节活动课的素材是探究月历中“3×3”正方形方块和“2×2”正方形方块中数字求和的规律. 这一数学活动素材的意义何在？即在活动中积累解决问题的经验和方法以利于学生思维的生长. 显然，仅仅探究月历中数与数的关系是不够的，所以教师在设计中，一方面利用方框形状的变化丰富研究的角度，另一方面以一般数阵中新的情境问题为载体，来检验学生是否具备迁移运用、融会贯通的能力，因为深层次思考也是高阶思维能力.

2. 创设合适的情境，唤醒学生的数学意识

数学活动课的意义在于通过积累数学基本活动经验，唤醒学生的数学意识，即将实际问题转化为数学问题. 教师创设或设计融入问题的情境，不仅能激发学生的兴趣，还能唤醒学生的符号意识、建模意识、运算意识、应用意识等数学意识，为学生高阶思维的培养做好铺垫.

3. 精心设计问题，让数学活动植入理性思维

问题是思维活动的原动力和牵引力[2]，学生的思维在问题的解决中能得以发展. 实践证明，好问题可将理性思维植入数学活动. 教师通过设计情境性问题、层次性问题、发散性问题、思辨性问题，让学生在观察、分析、验证、推理等一系列思维活动中表达、领悟、反思、内化和创造. 而教师在关键点进行有效追问，是思维品质进阶的有力杠杆，比如追问“题目问某数是否存在，是一个存在性问题，大家试一试在数阵中找找数的位置”有利于培养学生思维的严谨性，追问“为什么有些规律是延续的，有些规律不是延续的？这与什么有关呢？”引导学生对问题的特点、差异和本质进行思考，有利于培养学生思维的批判性和深刻性，提高学生学习的自主性.

数学家波利亚说过，“数学教育主要目的之一是发展学生解决问题的能力，教会学生思考. ”教材每一章节后都有数学活动，但因为课时，常常被教师忽略. 在常规教学中，数学活动课虽不是主体，但是笔者认为教师应利用好数学活动课这个平台，让学生在真实、开放、有趣、综合等情境中发现问题、分析问题、解决问题，从而促进学生发展高阶思维能力.

参考文献：

[1]林勤. 思维的跃迁：高阶思维能力的培养及教学方式[M]. 上海：华东师范大学出版社，2016.

[2]夏培培. 以问题为“驱动”发展学生数学高阶思维能力——以“几何最值问题”的专题探究为例[J]. 中学数学，2019（06）：44-46.