1969—2017 年拉萨强降水日数变化特征*

多典洛珠 丁真贡嘎 拉巴 潘多 边玛罗布

（1.西藏自治区气象台；2.西藏拉萨市气象局，西藏 拉萨 850000）

近年来，我国极端天气气候事件频发，台风、暴雨、高温、干旱、风雹、雪灾等气象灾害给人民生命财产安全和经济社会运行带来严重影响。

极端降水事件已逐渐成为国内专家学者研究的热点议题［1-4］。杨金虎等［2］针对中国西北近45a汛期极端降水事件的发生频次和分布特征进行了统计分析；张楠楠等［3］对宁夏中雨以上降水过程气候特征进行了研究，发现随着地势的差异，宁夏中雨及以上降水事件自北向南逐渐递增；邹立尧等［4］研究得出近60a 三江平原夏季强降水日数总体呈增多趋势，其中最多年比最少年偏多8.6d；吴丹等［5］通过阈值分析法将江淮流域不同测站汛期极端强降水事件进行统计分析，并定义了每个测站相应的阈值。

极端降水事件不仅会直接对社会、环境造成重要影响，持续性强降水事件还会致使洪涝灾害的发生［6］。在全球变暖气候大背景下［7,8］，西藏地区大部分极端降水指数呈现不显著的增加趋势［9］。西藏作为青藏高原的主体，本身地质环境脆弱，地形结构复杂多样，气象灾害多发易发。首府城市拉萨又是人口相对密集的地区，气象灾害给人民生命和财产安全造成的影响更大。通过分析2019—2021 年气象资料，拉萨市范围近90 余气象观测站共出现378 站次24h 降水量≥25mm，其中2站次24h降水量≥50mm。不仅如此，受城市特殊下垫面的影响，午后到傍晚时分更容易出现中小尺度的强对流天气，根据统计有314 个站次1h降水量≥10mm，其中22 站次1h 降水量≥20mm。极端性天气的频繁出现使气象灾害发生的突发性、极端性和不可预见性随之加强。因此，研究拉萨地区的强降水天气气候特征及其影响因子，有利于进一步揭示河谷地区天气气候特征，为该地区极端天气的预测和防范提供可参考依据。

近年来，针对拉萨地区强降水的研究也有很多，但是大多仅限于一两次天气个例的分析［10,11］，对强降水的长期变化及其成因分析较少。本文基于拉萨近49a（1969—2017）汛期降水资料，首先采用百分位法分析了拉萨强降水阈值，其次利用趋势系数、滑动t 检验和累积距平曲线以及Morlet 小波分析法对拉萨强降水的气候特征进行诊断分析，最后结合相关性分析进一步研究了拉萨强降水变化可能的影响因子。

1 资料与方法

1.1 资料

选取1969—2017 年拉萨站汛期（5—9 月）20:00至次日20:00 累积降水量分析了拉萨强降水日数的长期变化，利用日最高气温、日最低气温和两个时次（08:00 和20:00）探空资料分析了拉萨强降水日数变化可能的影响因子。

1.2 强降水日

按照中国气象局降水等级划分标准，将日降水量超过50mm 的降水事件，称为暴雨；日降水量超过25mm 的则视为大雨［12］。然而，对于不同地区来说，出现的降水概率、强度和造成的影响等存在很大的差异，在高原地区，受复杂地形和区域特殊天气气候的影响，完全用全国统一的日降水量来简单定义当地的极端降水事件是不合理的，需要根据当地的实际情况，因地制宜，研究出适合本地的强降水阈值。本文采用逐年日降水序列的第90 个百分位值作为强降水阈值［13］，根据计算得出拉萨近49a 强降水阈值为14.2mm，日降水量（R24）≥14.2mm 时定义为一次强降水日。

1.3 整层大气水汽含量和稳定度k 指数计算方法

1.3.1 整层大气水汽含量。一般情况下，在探空观测资料中，用温度露点差来表示各层高度上的湿度量。因此，要计算整层水汽含量［14］首先要通过温度露点差来确定各层的水汽压值。

式（1）中：a 和b 均代表常数，在水面饱和情况下a=17.26，b=35.86;在冰面饱和情况下取a=21.87,b=7.66,再通过水汽压值e 计算出比湿q:

式（2）中：e 表示水汽压，p 表示气压。最后利用比湿计算整层水汽含量的公式如下：

式（3）中，q 为比湿（g/kg）,Ps 为地面气压（hPa），Pz 为积分上限，取200hPa。

1.3.2 K 指数。K 指数［15］可以反映大气的层结稳定情况。K 指数越大（越小），层结越不稳定（稳定）。

式（4）中，T500 和T300 分别代表500hPa 和300hPa 的温度，Td500 代表500hPa 露点，(T-Td)400代表400hPa 温度露点差，K 指数计算式中第一项表示温度直减率，第二项表示低层水汽条件，第三项表示中层饱和程度。

1.4 分析方法

首先建立强降水日数序列与时间序列之间的一元线性回归方程：

式（5）中，y 为强降水日数，x 为时间序列，a为线性倾向率，当a ＞0（＜0）表示近49a 强降水日数有上升（下降）趋势，该方法主要用来评估强降水日数的长期变化趋势，之后分别采用累积距平曲线和Morlet 小波方法［16］分析了强降水日数的气候突变特征和周期变化，最后通过相关性分析讨论了强降水日数与其他气象要素之间的相互关系。

2 强降水日数变化趋势

2.1 长期趋势变化特征

为进一步分析拉萨强降水日数的长期变化特征，图1 给出了拉萨汛期强降水日数年际变化趋势，1969—2017 年强降水日数总体上呈增多趋势，其气候倾向率为0.6d/10a，通过了0.05 的显著性检验，表明强降水日数显著增多。其中，峰值出现在2014 年，共计17d；次峰值则分别出现于1995 年和2016 年，均为13d。近49a 强降水日数最少的年份为1992 年，只有2d；而次少的则为1975 年和1981 年，均为3d。同时，强降水日数年际变化幅度较大，最多年与最少年相差15d。

图1 1969—2017 年拉萨强降水日数变化特征

根据5 阶多项式拟合，可以看出，拉萨市强降水日数以波动的形式逐渐增多，20 世纪60 年代到70年代间呈递减趋势，此后整体为上升趋势，转折期在1980 年左右，特别是20 世纪90 年代和21 世纪10年代初经历了频繁出现强降水天气时期。

2.2 突变分析

为进一步分析强降水日数的多年序列是否存在气候突变，图2 给出了1969—2017 年强降水日数的标准化距平序列的10a 滑动t 检验和累积距平曲线，发现1989 年和1992 年分别为滑动t 统计量最小值和次小值，并且通过了0.05 显著性检验，即1989 年前后强降水日数距平值出现了明显的差异。从累积距平曲线的变化趋势可以得出：在1989 年前，降水日数距平表现为持续的下降趋势，以负距平为主，1989 年以后，降水日数距平表现为上升趋势，以正距平为主。说明1989 年前后降水日数变化趋势出现了明显的转折。

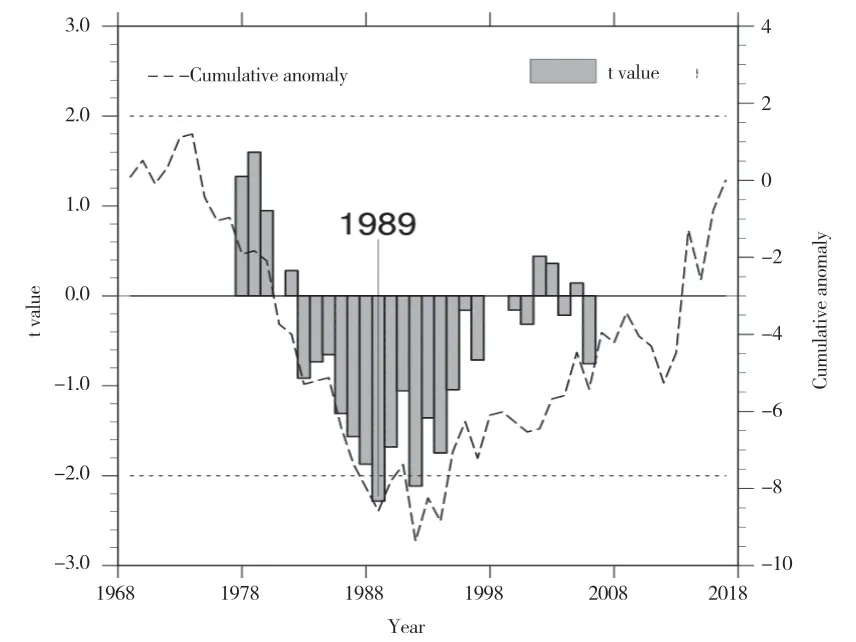
图2 1969—2017 年拉萨强降水日数标准化距平10a滑动t 检验及累积距平曲线

2.3 周期分析

小波变换具有多分辨率特点，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，能够有效提取气候序列在各种尺度扰动的周期变化。

图3 绘制了拉萨市近49a 强降水日数Morlet 小波分析，左图为周期变化，右图为小波功率谱，倒锥形为影响锥，网格线区域代表边缘区域，该区域周期变化具有一定的不确定性，对应右侧功率谱，当功率越大时等值线越密集。

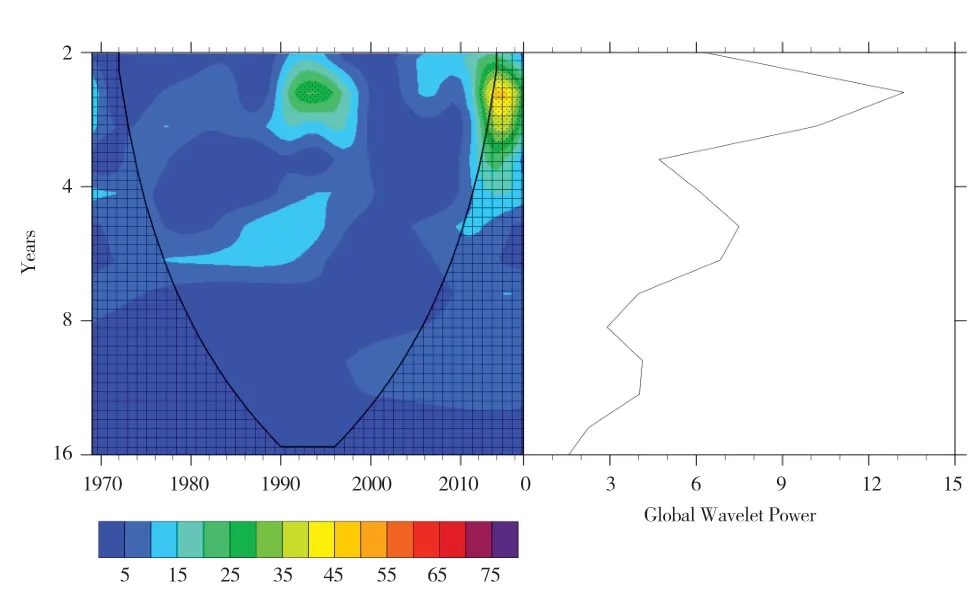
图3 1969—2017 年拉萨强降水日数小波分析

可以看出拉萨强降水日数存在准3a 和4a～6a 尺度的年际变化周期，其中主周期为3a，同时还存在4a～6a 的次周期。

3 强降水日数增多可能的影响因子

3.1 与大气水汽含量的相互关系

从产生降水的基本成因分析，降水形成的首要条件是水汽由源地输送到降水地区，水汽是大气中活跃多变的气象因子，水汽条件的差异直接影响到是否发生降水，更是决定降水强度的根本因素。拉萨地区地处雅鲁藏布江河谷地区，降水日变化特征非常明显，从多年平均降水强度日变化上看，一般存在两个峰值，第一个峰值出现在午后，第二个峰值出现在夜间［17］，因此选取拉萨站08 时（北京时，下同）探空观测数据和20 时探空观测数据，分别计算出汛期逐日大气整层水汽含量并进行算数平均，从而得到逐年汛期平均整层水汽含量。将整层水汽含量序列与强降水日数序列进行相关性分析。

由于1979—2014 年期间探空观测资料缺测率相对较少，本文选取该时段探空资料与汛期拉萨强降水日数进行对比分析，图4 给出了降水日数与汛期降水出现日平均08 时和20 时整层水汽含量之间的时序图，可以看出强降水日数和水汽含量之间的变化趋势基本一致，通过相关性分析发现强降水日数与两个时次的整层水汽含量之间呈现正相关，相关系数分别达到了0.42 和0.41，均通过了0.01 的显著性检验。说明，拉萨的强降水日数分别与08 时和20 时大气整层水汽含量之间有较好的相关性，当汛期平均整层水汽含量高（低）时强降水日数多（少）。

图4 1979—2014 年拉萨强降水日数分别与汛期降水日08 时（a）和20 时（b）整层水汽含量之间的相关性

3.2 与大气稳定度K 指数的关系

一般情况下,形成暴雨的三个主要条件分别为充足的水汽条件、较强的垂直上升运动和大气层结不稳定条件。K 指数往往可以较好的反映大气的层结稳定度。与3.1 节中的统计方法一样，利用拉萨站汛期降水出现日08 时和20 时的探空资料计算了逐日k 指数，通过算数平均得到汛期平均K 指数序列。根据相关性分析结果（图5），拉萨强降水日数与K 指数呈现正相关关系，当K 指数越大（小）时大气层结越不稳定（稳定），强降水日数越多（少），对比来看，强降水日数与20 时K 指数之间的相关系数大于08 时K 指数，通过了0.05 的显著水平。说明强降水日数和下午的不稳定条件之间的关系更加密切，这可能与拉萨地区午后易出现对流性天气有关。

图5 1979—2014 年拉萨强降水日数分别与汛期降水日08 时（a）和20 时（b）平均k 指数之间的相关性

3.3 与地面气温之间的关系

降水和气温之间的关系也十分密切，当白天有天气系统过境时，天空云量往往较多，此时最高气温往往偏低；而夜间有天气系统过境时，天空云量较多，云层保温效应明显，易造成最低气温上升。

分析拉萨强降水日数与地面气温的相关性，表1给出了近49a 汛期降水出现日平均最低气温、最高气温和气温日较差与强降水日数之间的相关系数。可以看出，强降水日数与日最低气温关系密切呈现正相关，通过了0.05 的显著水平。拉萨地区降水主要集中在夜间，平均夜雨率达到了75%［18］，而日最低气温一般出现在清晨06:00～08:00 时之间，因此，当有降水天气系统过境时，在云层的保温效应和潜热释放的双重作用下，日最低气温往往偏高。

表1 汛期强降水日数与降水日平均地面气温之间的相关性

此外，强降水日数与气温日较差呈现反相关关系，相关系数达到了-0.34，通过了0.01 的显著水平。由于气温日较差是一天中最高气温和最低气温的差值，再次说明，降水天气系统过境时高温偏低、低温偏高，易造成气温日较差偏小，因此，强降水日数越多时，平均气温日较差越小。

4 小结

本文首先利用1969—2017 年拉萨站汛期地面和探空观测资料，分析了拉萨地区近49a 强降水日数的长期变化趋势、突变特征和周期变化，其次分析了强降水日数与其他气象要素之间的相互关系，得到如下主要结论：

（1）拉萨近49a 强降水日数呈现显著的增多趋势（增多率为0.6d/10a），强降水日数最多的年份出现在2014 年，达到了17d，强降水日数最少的年份为1992 年，只有2d；在19 世纪80 年代强降水日数出现了由少到多的突变，突变年为1989 年；强降水日数在近49a 存在准3a 的主周期和4a～6a 的次周期。

（2）强降水日数与大气整层水汽含量呈现正相关关系，与08 时和20 时整层水汽含量的相关系数分别达到了0.42 和0.41 均通过了0.01 的显著水平，强降水日数与K 指数也呈现正相关关系，其中与20 时K 指数之间的相关系数高于08 时，通过了0.05 的显著水平。

（3）强降水日数与地面日最低气温呈现显著的正相关关系，与气温日较差呈现显著的负相关关系，与地面最高气温相关性不明显；当强降水日数越多（越少）时日最低气温越高（低）而平均气温日较差越小（大）。