基于层次分析法的林芝地区滑坡灾害稳定性模糊综合评价*

2023-04-11林琴郭永刚苏立彬渠士豪

西藏科技 2023年1期

林琴郭永刚苏立彬渠士豪

（西藏农牧学院水利土木工程学院，西藏林芝 860000）

滑坡是重要的地质灾害之一，其影响程度仅次于地震，且滑坡具有的突发性特点与地震相似，多发生在山区。藏东南地区地质灾害广泛分布，地质灾害（图1 所示）的类型有滑坡、泥石流、崩塌、地面塌陷、地面沉降、地裂缝和土地冻融，由于不同区域的地形地貌和地理位置的不同，地质条件、水文条件和岩土特征差异较大，地质灾害分布不均，研究区以泥石流、滑坡、崩塌灾害为主（表1 所示）；可以看出地质灾害比例中滑坡灾害所占比例较高。要想有效地减轻滑坡对人口、经济、社会环境造成的影响，就要对滑坡灾害发生的机理与规律深入分析，弄清楚哪些地方容易发生滑坡，哪些地方发生滑坡的几率大。霍张丽等人采用模糊数学中的模糊综合判定方法建立了滑坡稳定性评价模型，对各影响因子进行等级标准分类并得出权重［1］；本文采用层次分析法(AHP)对研究区的滑坡稳定性进行了研究，层次分析法由美国运筹学家T.L.saaty 于20 世纪70 年代提出，它是一种定性与定量相结合的决策分析方法，广泛应用于地质灾害领域［2］。毛宇昆通过卡方检验对所有可能的影响因子进行分析计算，最后得出几个适合研究区内影响滑坡稳定性的评价因子，使用随机森林、LightGBM 等机器学习方法构建滑坡稳定性评价模型并进行模型融合，在此基础上开发设计了滑坡稳定性评价系统［3］；卢崇明利用有限元分析软件Midas/GTS，采用莫尔-库仑模型及屈服准则对坡体进行数值模拟计算，根据稳定性分析结果，结合滑坡工程的实际情况，利用模糊层次分析法对设计方案进行了优选研究，进一步验证层次分析法优选结果的可靠性［4］；李朋丽将平均坡度等6 个影响滑坡稳定性的因素作为评价指标,建立滑坡数据库，并利用MATLAB 对ANNs 进行了设计、权值初始化,在此基础上对滑坡稳定性分析与预测模型进行了训练。结果表明：样本训练结果和实际情况基本吻合,证明该模型能够符合工程实际［5］；胡安龙等人在论述SVM 交叉验证法粒子群优化算法、GA等理论基础上，构建滑坡稳定性预测模型，结果表明: 遗传算法优化的支持向量机滑坡稳定性预测模型效果明显胜于粒子群优化算法和交叉验证法优化的预测模型［6］。本文基于层次分析法对林芝地区滑坡灾害稳定性进行模糊综合评价，层次分析法是一种有效的方法，但单纯的层次分析法并不能完全反应人类的思维方式。基于层次分析法的模糊综合判定可以使用设定的标准和替代方式做出更灵活、更高效和现实的决策。

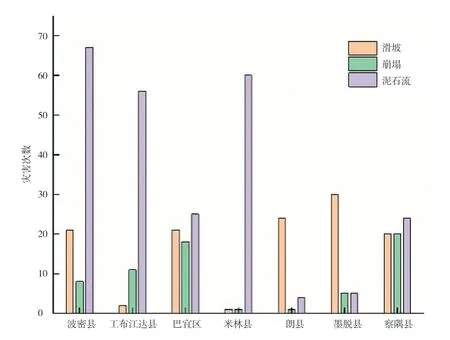
图1 西藏自治区地质灾害规模统计

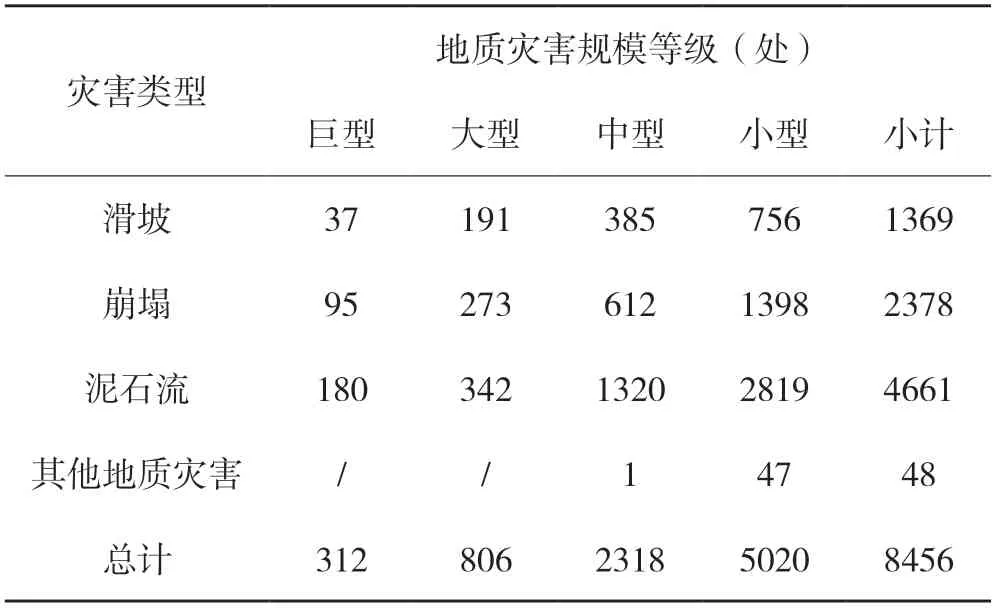
表1 2019 年藏东南地质灾害类

1 研究区概况

研究区位于西藏东南部和雅鲁藏布江下游，26°52′N 到30°40′N，92°09′E 到98°47′E 之间，西部和西南部分别与拉萨、山南毗邻，东部是昌都市，北部是那曲地区，南部与印度、缅甸两国相接壤，海拔高差与地形起伏大，大多数地区海拔在3000 米左右。区域地质构造活跃，内外动力影响剧烈，气候变化异常，滑坡发生频繁。

2 基于GIS 的滑坡易发地区

2.1 数据来源

滑坡稳定性所用的基础数据见表2。

表2 数据目录

2.2 指标体系建立

本文结合研究区的地理环境和灾害特征，充分考虑所需资料能否获取，研究尺度、精度和范围的大小及要求等，再综合大量已有研究成果和野外地质的实质调查结果，最终确定评价因子。

2.2.1 高程。研究区域高程，如图2 所示，在GIS 中利用空间分析工具得出每个滑坡点的高程（图3 所示），可知高程在1500～4500 之间，易发生滑坡灾害。随着海拔持续地上升，到一定的临界值时，气温越低，人口密度越小，人类活动强度越小，发生滑坡的可能性就越小。

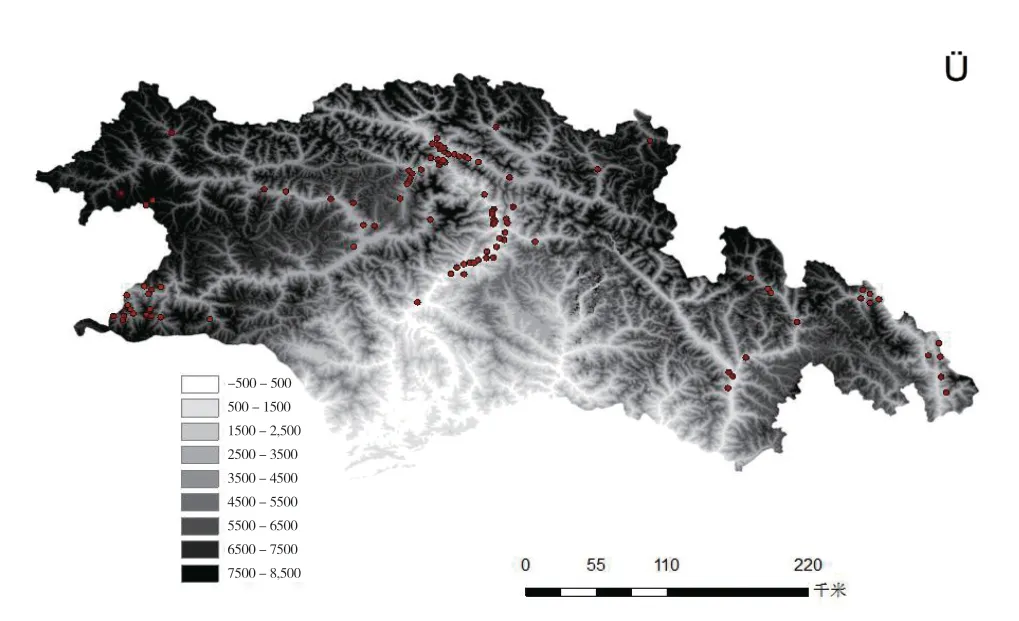
图2 林芝地区高程图

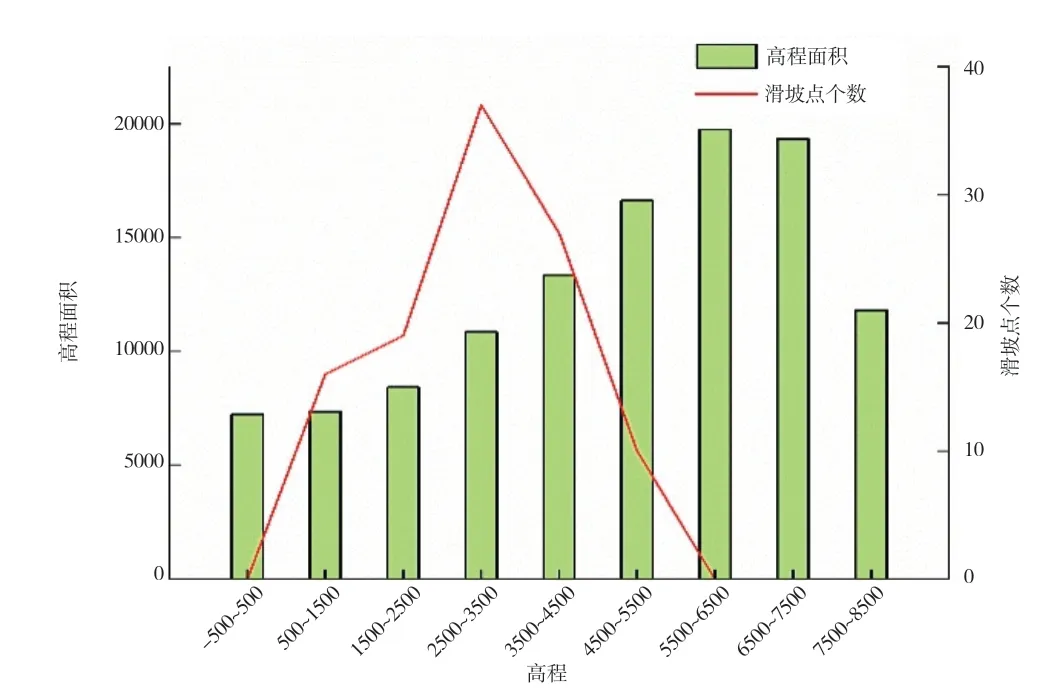
图3 林芝地区高程分布图

2.2.2 坡度。在影响滑坡因素中，坡度所占的权重最高［7］。根据研究区域的实际情况，将坡度分为9 个等级（图4 所示），再利用栅格转面工具算出每个滑坡点的坡度（图5 所示）。结果表明，当山体的坡度在10 度到40 度之间时，山坡坡度大，山地陡峭，河流谷坡陡峻，形成深切的高山峡谷地貌，山体高陡临空面发育，出现侧向拉应变，促进卸荷裂隙发育和岩体内部应力的释放，造成表层岩体结构松弛，发生滑坡的概率最大。

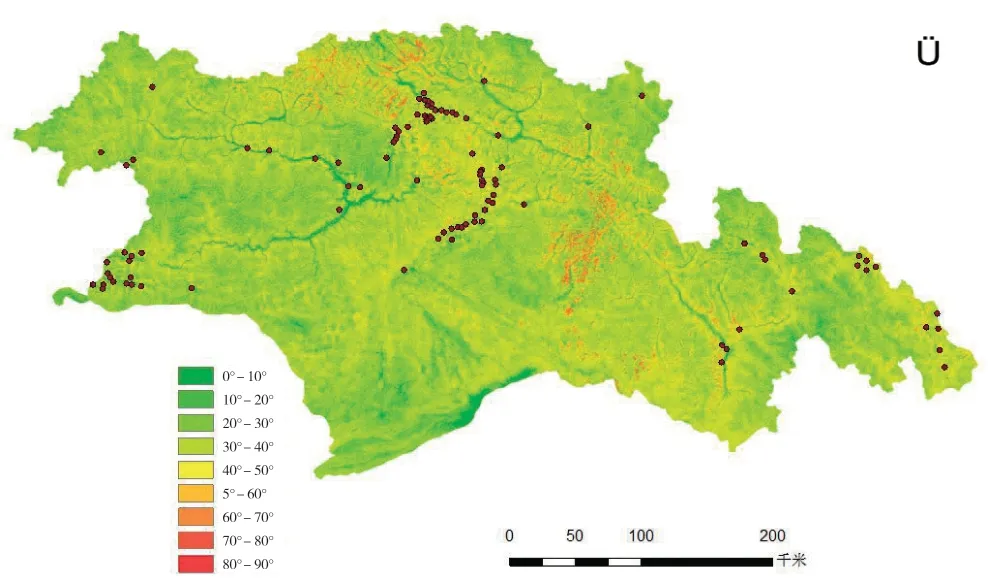
图4 林芝地区坡度分级图

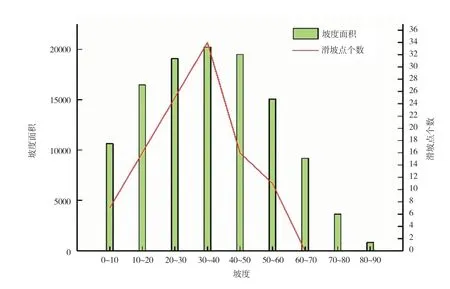
图5 坡度分类及面积占比

2.2.3 道路。林芝地区地质地貌独特，其气候特征为高原高寒气候，土壤中的养分散布不均衡，边坡的土质极其疏松且不稳定，再加上风蚀和水蚀的外力作用，很容易发生水土流失现象，最终可能会造成公路坍塌和山体滑坡等结果［8］。利用ARCGIS 空间分析功能，对道路数据建立100 米为间隔的缓冲区(图6 所示)，各滑坡点距道路距离见（图7 所示），由表可知，距离道路越近，越容易发生滑坡灾害，一些修筑道路等人类工程活动加上不利天气因素影响，很大概率会造成滑坡。

图6 林芝地区主要道路图

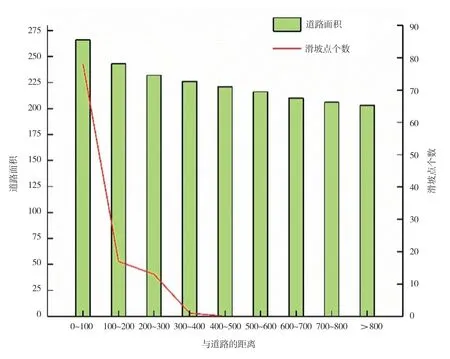
图7 距道路距离与滑坡个数

2.2.4 水系。影响滑坡发育的条件中，水系是其中的一个重要因素，河流的冲刷和开挖会影响边坡的稳定性，发生滑坡的可能性也会增大［9］。林芝地区的河流主要由怒江、雅鲁藏布江、尼洋曲等组成。本文在GIS 的平台上，以100 米为间隔，生成9 个河流缓冲区（图8 所示），在计算出距河流不同距离的面积与滑坡点距河流的位置（图9 所示），由表可知，越靠近河流，河流侵蚀、水土流失、土壤软化现象愈加明显，越容易发生滑坡灾害。

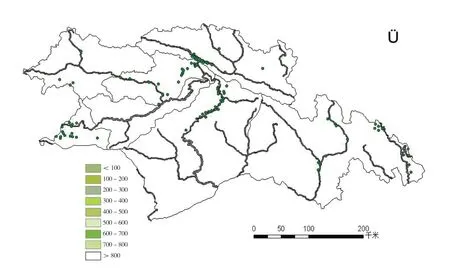
图8 林芝地区河流缓冲区

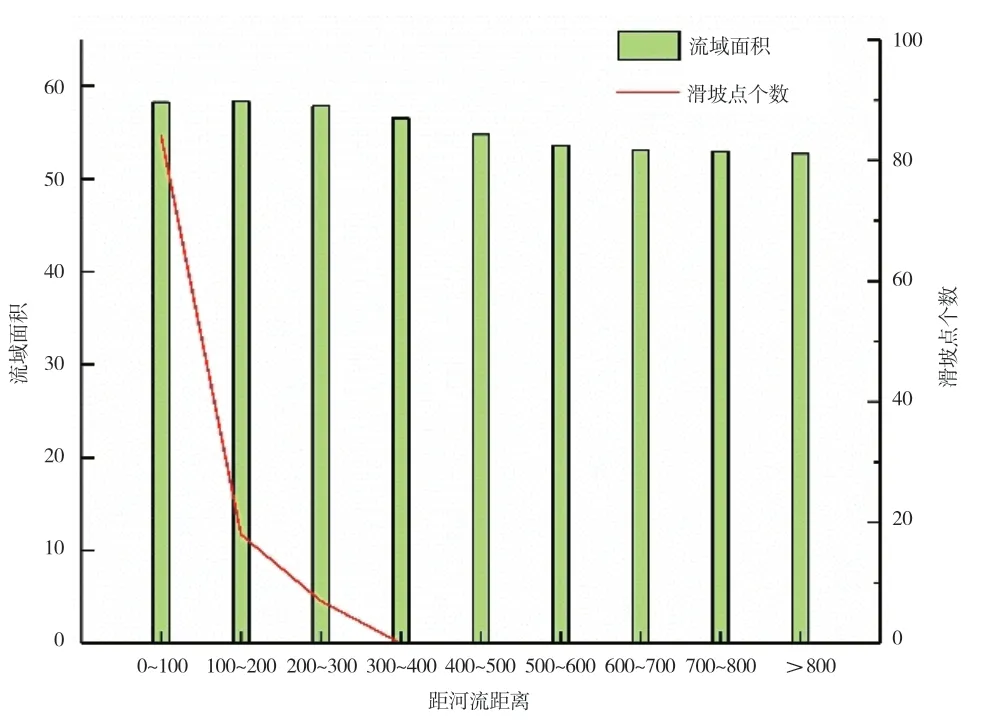
图9 距河流距离与滑坡个数

2.2.5 断裂带。研究区域位于印度洋板块和亚欧大陆板块碰撞断裂地带，该地带地质灾害发生较为频繁。本文将研究区域的断裂带以100 米为距离生成缓冲区（图10 所示）由生成的距断裂带面积与滑坡点信息（图11 所示）可知，越靠近断裂带发生滑坡灾害的可能性越大。

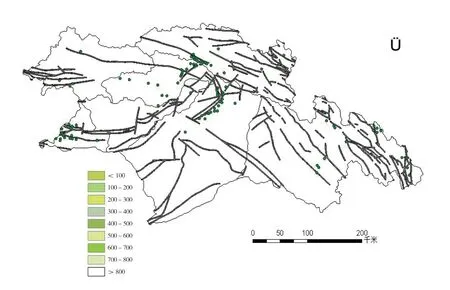
图10 林芝地区断裂带分布图

图11 距断裂带距离与滑坡个数

2.2.6 土地利用。通过遥感影像进行目视解译，生成不同土地利用类型（图12 所示）的面积及各部分面积所占的比例（图13 所示），由图12 及图13 中可以看出，林芝地区滑坡灾害大部分发生在林地，且林地面积几乎占了总面积的一半。

图12 林芝地区土地利用类型

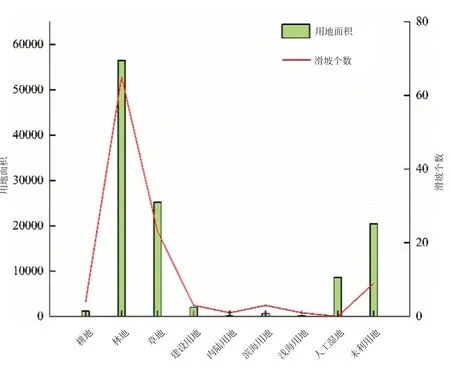
图13 土地利用类型及面积占比

2.2.7 地层岩性。林芝地区内地层岩性极为混杂，从中生界及至元古界均有涉及。不同岩土体的化学物理性质、坚硬程度、抗风化能力等性质均不相同［10］。本文根据岩石的坚硬程度将林芝地区的岩土体分成5种类型：坚硬、较坚硬、较软弱、软弱和极软弱（图14 所示）；并将生成滑坡点个数与岩土体坚硬程度图（图15 所示），结果表明：68%的滑坡发生在白垩统、二叠统、元古界中的板岩、砂岩、角闪片岩和片麻岩，18%的滑坡发生在白垩纪中的花岗岩、板岩，说明林芝地区的滑坡在片岩、砂岩、板岩等软硬相间的岩层中稳定性较低。

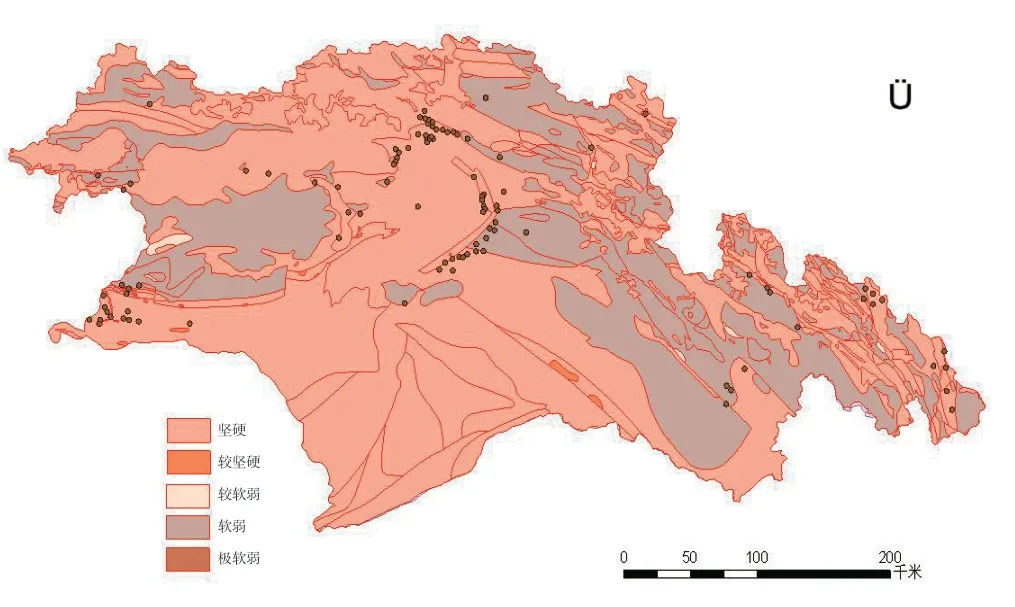
图14 林芝地区地层岩性

图15 滑坡灾害点个数与岩土体坚硬程度图

3 评价方法及模型

3.1 层次分析法

层次分析法可用于多目标优化问题，通过给定每个因素的权重占比，将多对象问题转变为可以解决的单目标规划问题，用来解决一些方案选择问题。层次分析法通过整理构建系统各要素之间的关联，建立上下层两两之间判断矩阵，一致性通过之后填充权重矩阵得出结果。

3.1.1 构建层次结构模型。通过收集到的滑坡灾害数据并分析林芝地区滑坡发育的结构特性、地质情况等因素，建立层次结构模型（图16 所示）。

图16 林芝地区滑坡灾害稳定性评价指标

3.1.2 构造判断矩阵。对于已经选定的评价指标，通过专家评分法将影响因素与两种比较的构造矩阵模型进行比较，生成判断矩阵［11］（表3～6）。

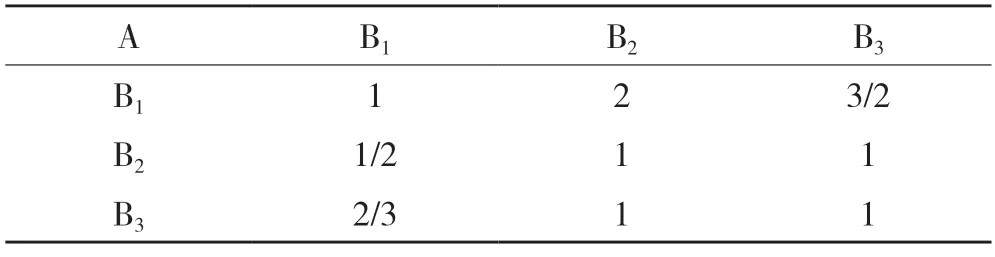
表3 A-B 判断矩阵

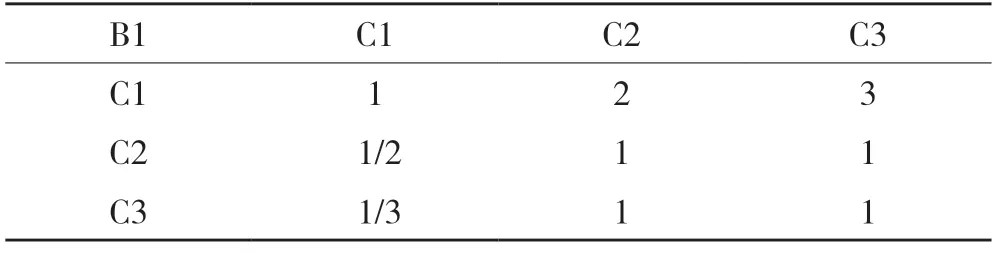
表4 B1-C 判断矩阵

表5 B2-C 判断矩阵

表6 B3-C 判断矩阵

3.1.3 一致性检验。对判断矩阵进行分析，并用公式（1）验证判断矩阵的一致性。

式中：λ 为矩阵最大特征值；W 为各影响因子的权重值，也是特征向量；A 为影响因子矩阵；n 表示矩阵的阶数；CI 表示一致性指标；RI 表示平均随机一致性指标；CR 表示一致性比例。若CR ＜0.1，说明此矩阵的权重分布合理，否则需要重新对权重赋值调整矩阵。根据公式(1)得到A-B 矩阵对应特征值为极值，为3.009，CI 值计算后为0.005，CR 值为0.009；B1-C矩阵对应的特征值的极值为3.018，CI值为0.009，CR 值为0.016；B2-C 矩阵对应的最大特征值为2，CI、RI、CR 值均为0；B3-C 矩阵对应的最大特征值为3.054，CI 值通过计算后为0.027，CR 值为0.047；ABC 三层的CR 值均小于0.1，符合一致性检验。用和积法按列归一化之后得到各影响因子所占权重（表7 所示）。通过对影响因子权重的计算，发现地区内影响稳定性最大的因素为坡度，之后水系分布、道路分布、断裂带分布、地层岩性分布、行政区划图、土地利用类型和DEM 图的影响程度降低。

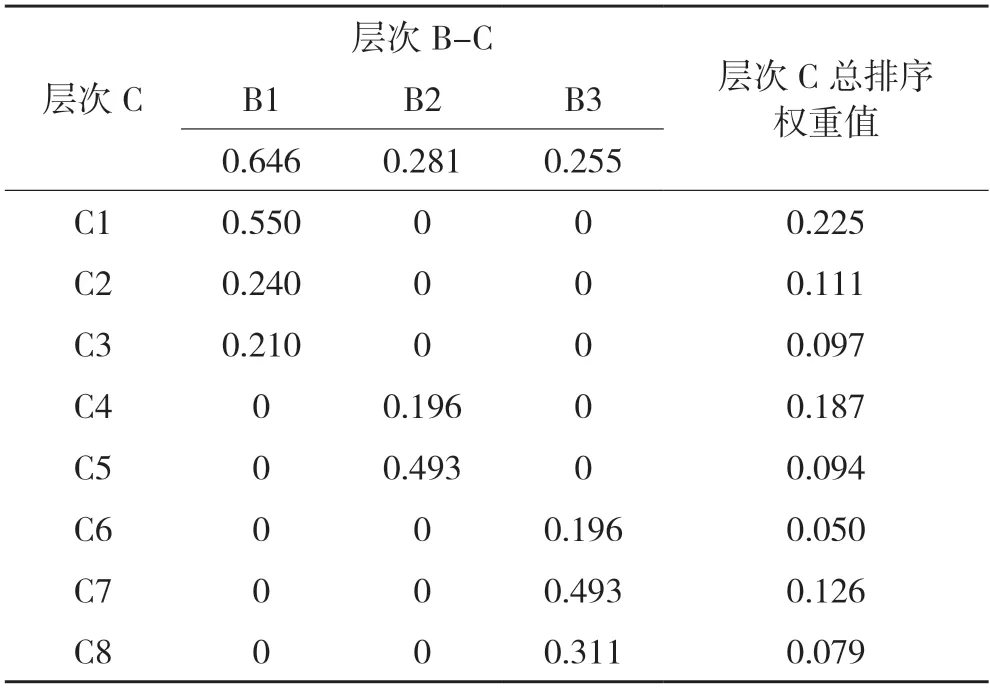
表7 A-C 层次总排序

3.2 模糊综合评价滑坡稳定性

3.2.1 模糊综合判定。模糊综合判定基于模糊数学理论，对实际的问题提供综合评价，应用模糊关系合成原理，将一些边界不清、不易定量的因素定量化，进而进行综合性评价的一种方法。近年来，模糊综合判定方法逐渐被运用到地质灾害领域中。本文将地质因素、背景因素、环境因素中的8 个评价指标，生成评价指标I 低稳定性、Ⅱ较低稳定性、Ⅲ中稳定区、Ⅳ较高稳定区、Ⅴ高稳定标准（表8 所示）。

表8 评价指标稳定性分级标准

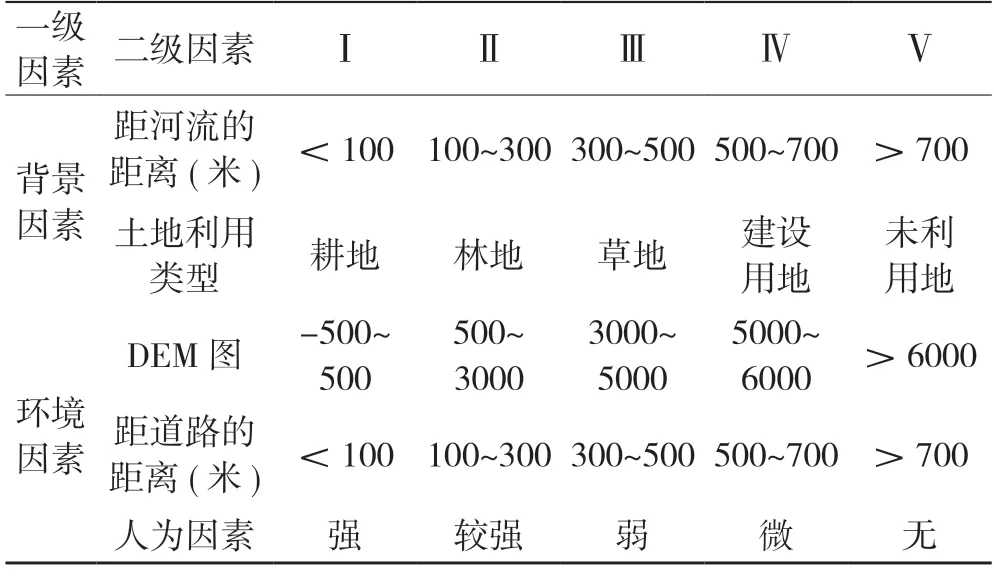
表8 （续）

3.2.2 稳定性评价。对生成的滑坡根据公式（2）进行稳定性评价，具体计算公式如下：

式中：A 为滑坡稳定性评价的最终结果向量，W为上文中通过层次分析法得出的各影响因子的特征向量，A1至An为二级评价因子对一级的特征向量，R1至Rn为隶属关系矩阵，“O”为模糊算子，本文采用加权平均型模糊算子。

4 滑坡稳定性评价结果

将地质因素、背景因素、环境因素中的8 个评价指标，生成评价指标稳定性分级标准（表9 所示）后，对图15 中的影响因子采用梯形隶属度函数构建评价因子的特征向量，得到影响因子的隶属度结果（表10 所示），再利用层次分析法得出的各影响因子的特征向量与隶属度矩阵进行加权平均，并进行归一化，得出稳定性评价结果为（0.105,0.5929,0.2866,0,0）［11］。在此基础上，利用生成的权重比，采用栅格重分类工具，按照自然间距分类方法将滑坡稳定性结果栅格图分成低稳定区、较低稳定区、中稳定区、较高稳定区、高稳定区5 个等级，得到林芝地区稳定性分区图（图17 所示），图层颜色越浅代表滑坡越不稳定，每个滑坡点对应的滑坡稳定性等级（图18 所示）。

表9 评价指标稳定性分级标准

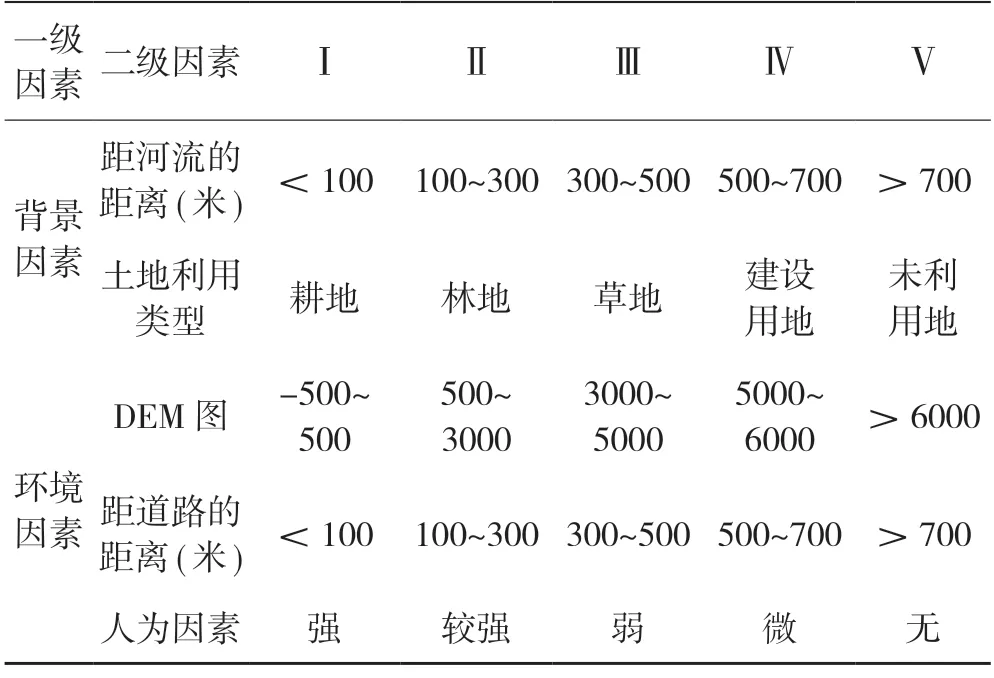
表9 （续）

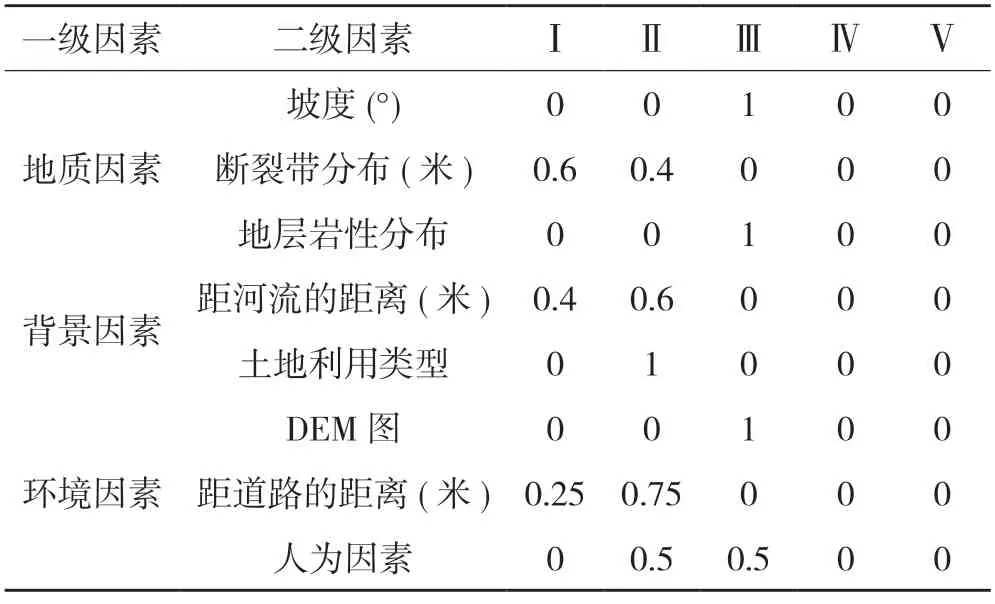
表10 影响因子隶属度结果

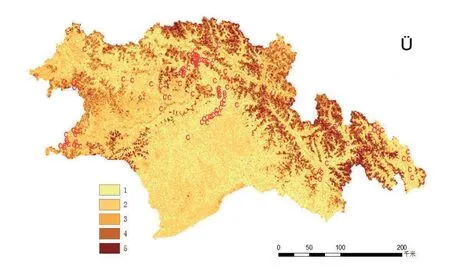
图17 滑坡稳定性评价分区图

图18 滑坡稳定性等级面积及滑坡点个数

结果表明：林芝地区的滑坡灾害易发生在1500～4500高程之间，坡度在20～40 之间，距道路、河流、断裂带200 米以内的范围，应在此类地点采取监控手段，预防更多滑坡灾害的发生。低稳定区的面积为28887km2,占林芝地区总面积的25.2%，覆盖易贡-索通-波朗段，朗县西南部登木附近、察隅县东南怒江附近及墨脱的绝大部分地区；较低稳定区的面积为48336km2,占总面积的42.2%，涵盖工布江达西部娘蒲，金达地区；中稳定区、较高稳定区、高稳定区的面积一共37425km2,占总面积的32.6%，包括察隅县北部的德拉，贡日嘎布曲附近及波密东北部康玉及东部松宗的大部分地区。再根据图18 对滑坡点进行验证，在Ⅱ区有67 个滑坡点，占滑坡总数的61.5%.结果表明：模糊综合判定方法对林芝地区滑坡稳定性进行评价具有较高准确性，对Ⅱ的隶属度最大，滑坡类型属于较低稳定性。