“周”是前提，“长”是本质——关于“周长的认识”的学情分析、教材对比与教学实践

重庆市梁平区力帆光彩小学（405200） 李小元

“周长的认识”一课是“周长”单元的第一课时，引导学生挖掘周长概念的本质，从而建立正确的周长概念是本节课的重点。笔者试图从学情调查中确定教学起点，从人教版、北师大版、苏教版教材的对比分析中确立教学重心，从课堂实践中探寻教学路径。

一、学情调查，明确教学起点

笔者经常在公开课中听“周长的认识”一课，发现大多数教师会在第一个教学环节花大量时间让学生去指认实物或平面图形一周的边线，从而让学生感知“一周”和“封闭”，建立“封闭图形”和“一周”这两个概念。对于这样的教学，笔者有一些疑惑：学生真的对“一周”和“封闭”一无所知吗？为此，笔者抽取三年级一个班的38 名学生为样本，在教学“周长的认识”一课前进行了一次学情调查。

［调查题目1］

下面几个图形中，哪些是封闭图形？请你在封闭图形下面的括号里画“√”。

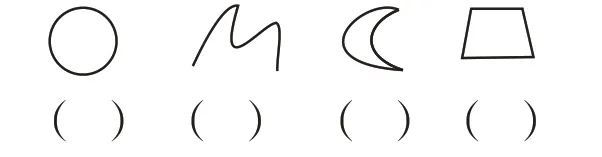
［调查结果］

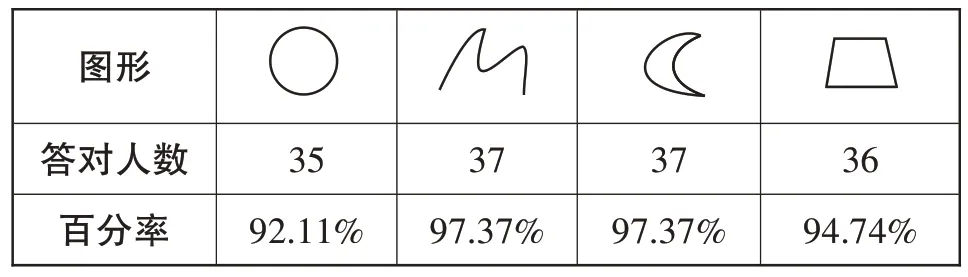
图形答对人数百分率35 92.11%37 97.37%37 97.37%36 94.74%

［结果分析］

从调查结果看，大多数学生都能正确判断封闭图形。在与回答不正确的学生交谈时，笔者指着第一个图形“圆”与第二个曲线图形问：“对比一下，它们有什么不同？”其中一名学生说：“第二个曲线图形的线没有封口。”笔者顺势指出第一个图形“圆”是封闭图形，然后让学生对调查题目1 重新判断，学生给出了正确的回答。由此说明学生对图形的封闭性有一定的理解。

［调查题目2］

请用红笔描出下面图形的“一周”。

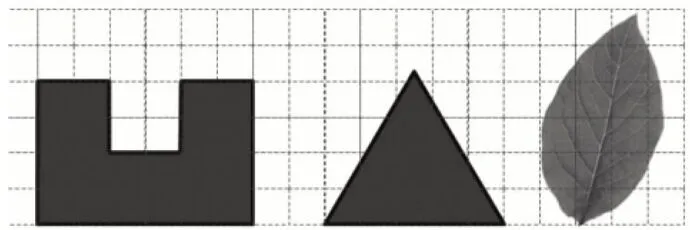
［调查结果］

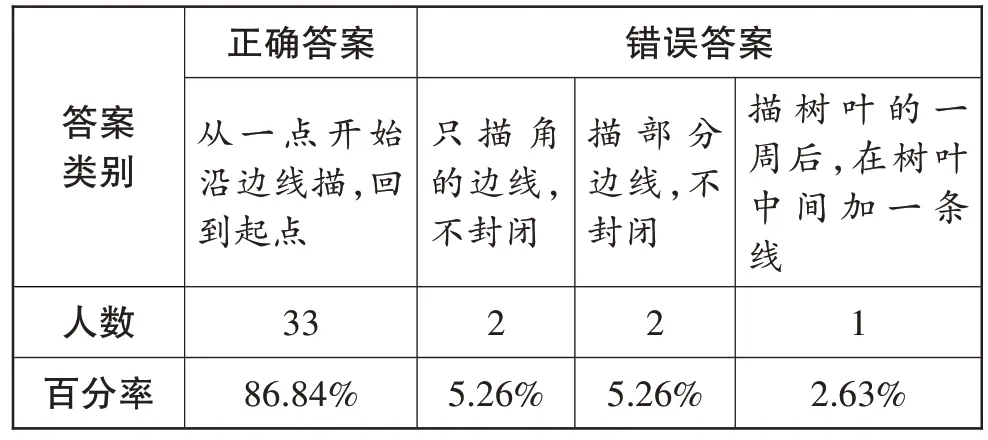
答案类别人数百分率正确答案从一点开始沿边线描，回到起点33 86.84%错误答案只描角的边线，不封闭2 5.26%描部分边线，不封闭2 5.26%描树叶的一周后，在树叶中间加一条线1 2.63%

［结果分析］

从调查结果看，学生对“一周”和“封闭”并不陌生，多数学生不但能描出图形的一周，还能区分图形是否封闭，认为封闭图形才有“一周”。有2 名学生只描角的边线，没有连接所有边线，还有2 名学生只描图形的部分边线，没有将所有边线连接。测试后，笔者对做错的5 名学生分别进行了访谈，笔者问：“你画的是图形的‘一周’吗？”随后4 名“只描了部分边线”的学生都正确描出了这几个图形的一周，“描树叶的一周后在树叶中间加一条线”的学生擦掉了树叶中间的那一条线。由此可见，尽管周长的概念是在“一周”的基础上拓展的，但是在“周长的认识”教学中，用较少的时间激活学生关于“一周”与“封闭”的经验就可以了，不必开展过多关于“一周”和“封闭”的数学活动。

二、教材对比，明确教学重心

1.教学路径对比

笔者从揭示概念、理解概念、应用概念三个方面分别对人教版、北师大版、苏教版教材提供的教学路径进行了梳理，整理结果见表1。

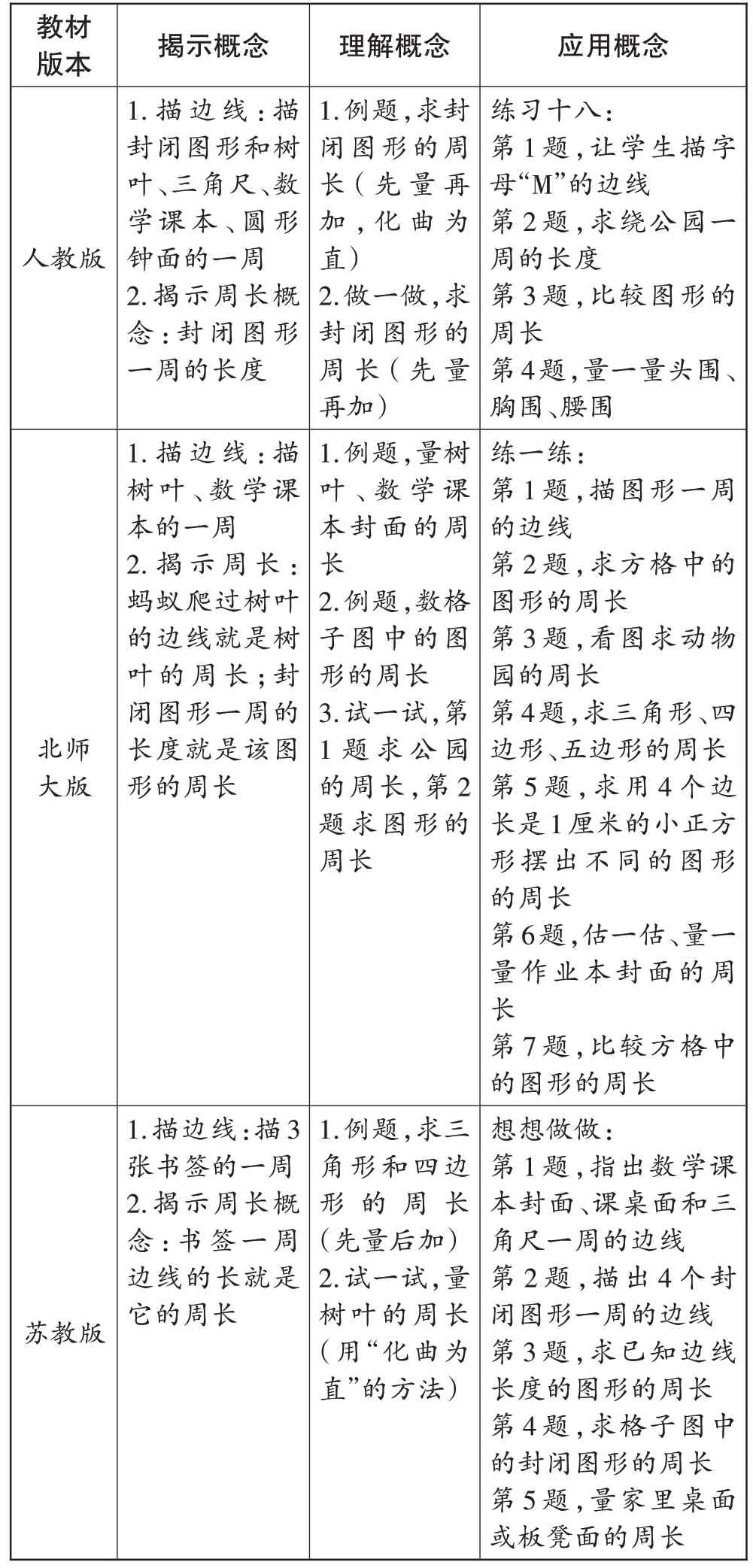
表1 三个版本教材的对比

对比分析人教版、北师大版、苏教版教材中关于“周长的认识”这一内容，笔者发现，三个版本教材呈现的教学路径非常相似。第一环节：描边线，揭示“一周”，概括周长的概念（封闭图形一周的长度即该图形的周长）。第二环节：通过先量（数）再加、“化曲为直”等方法求图形的周长，理解周长概念的本质。第三环节：通过多层次的求图形周长的活动，加深对周长概念的理解，为周长的计算教学打好基础。

笔者还发现，人教版和北师大版教材都安排了一道比较图形的周长的练习题。这也引发笔者对本节课教学的新构思：本课第二环节已经渗透了“先量（数）再求和，得到周长”的思路，学生应该会运用这种思路来比较两个图形的周长。教学中还可以尝试增加“先平移再比较”这种思维方式，让学生从一一对应的视角理解“如果两个图形对应边的长度相等，那么这两个图形的周长也相等”。

2.教学活动对比

笔者对比分析人教版、北师大版、苏教版教材中提供的学习素材和练习作业，将数学活动方式分类统计（见表2）。

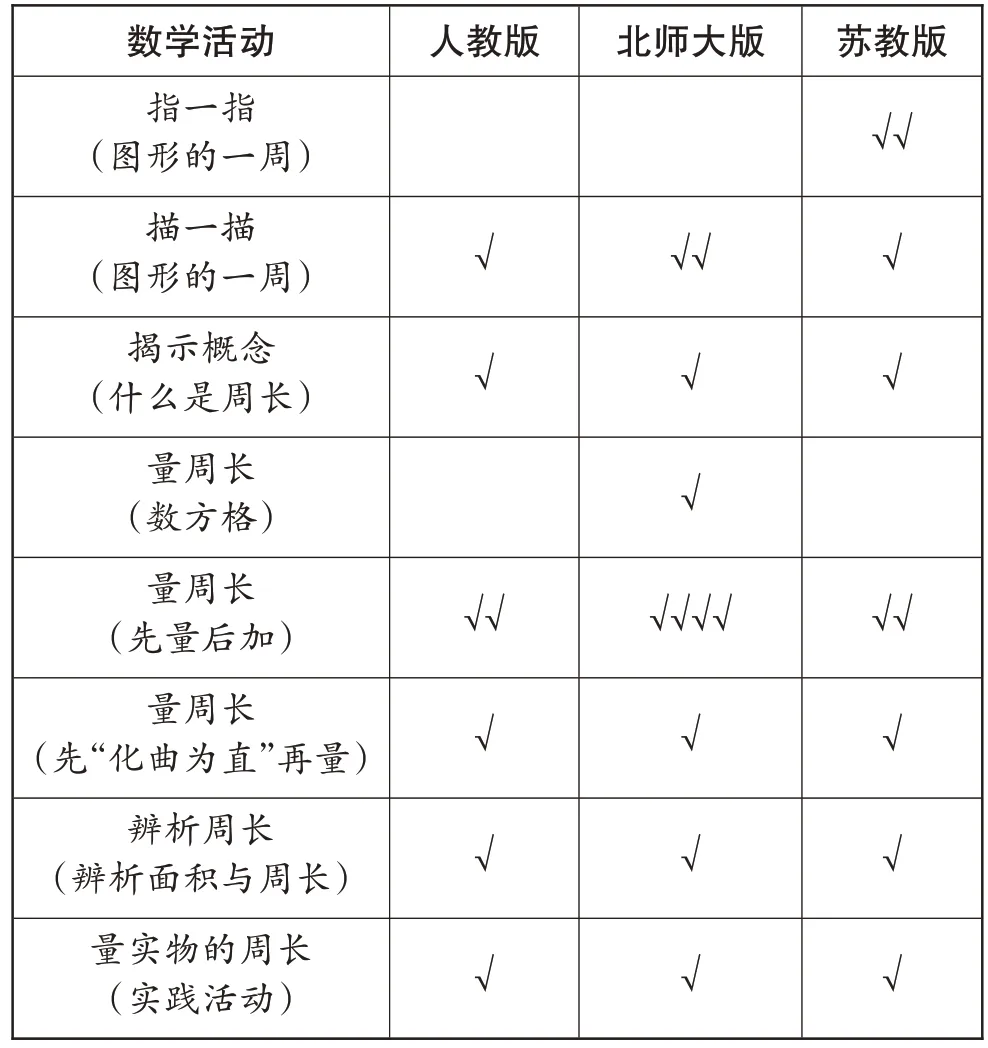
表2 数学活动方式

从表2 可以看出，只有苏教版教材安排了让学生指出封闭图形“一周”边线的活动。三个版本的教材都只安排了少量的描一描封闭图形“一周”的活动。

虽然不同教材提供的活动各不相同，但都把活动重心放在周长的本质——“长”的理解和应用上。人教版教材和苏教版教材都安排了3 个量图形周长的活动，其中，2 个先量线段的长度再相加的活动，1 个先“化曲为直”再量周长的活动。而北师大版教材更加重视利用多种方法量图形周长的活动，共安排了6 个活动，1 个数方格得周长的活动，4 个先量后加得周长的活动，1 个先“化曲为直”再量周长的活动。

教学中，教师应该重视这几个活动，让学生想办法量图形的周长，在格子图中数图形的周长，量多边形的各边长再相加得到图形的周长，通过量、数、加、“化曲为直”等方式，让学生理解“周长是封闭图形的边长之和”。

三、课堂实践，明确教学路径

1.辨别“封闭”和“一周”

操作：出示几根长度都是20 厘米的线，教师分别弯折后，在展台上展示（如图1）。

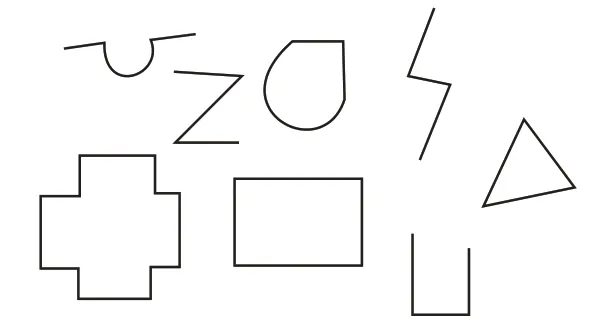
图1

师：哪些图形是封闭的？哪些图形是不封闭的？

封闭图形：

不封闭图形：

师：你们是怎么区分的？

生1：看图形的边线是否首尾相连。

师：封闭图形与不封闭图形有什么不同点？

生2：封闭图形有“一周”，不封闭的图形没有“一周”。

2.揭示周长概念

师：每根线的长度是20 厘米，弯折成这些图形后，现在它们的长度是多少？

生1：不管是封闭图形还是不封闭图形，这根线的长度都是20厘米。

师：同样都有长度，有什么不同的地方？

生2：围成封闭图形的这根线的长度是该图形一周的长度。封闭图形一周的长度叫周长。

师：不封闭图形有周长吗？

生3：不封闭图形没有周长。

［思考］

此环节通过两个活动帮助学生初步建立周长概念。

第一个活动，促进学生观察与比较，发现封闭图形与不封闭图形的不同点——封闭图形的线首尾相连，不封闭图形的线首尾不相连，从而帮助学生建立起“一周”的概念。

第二个活动，以“每根线的长度是20 厘米，弯折成这些图形后，现在它们的长度是多少？”这个问题引导学生关注长度，“同样都有长度，有什么不同的地方？”这个问题继续将学生的目光引到“一周”上。通过这两个问题，学生对周长的认识逐渐清晰，明白周长就是封闭图形一周的长度。此时教师继续追问：“不封闭图形有周长吗？”学生充分体会到周长与线段长度的区别就在于是否有“周”这个前提。

3.理解周长概念

活动：测量与计算图2 中各图形的周长（每个方格的边长都是1厘米）。

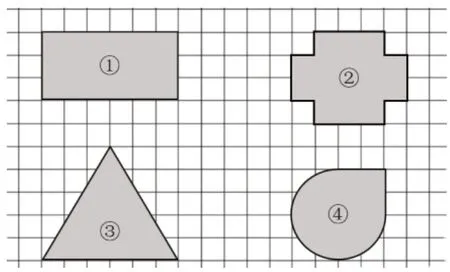
图2

师：要想知道它们的周长是多少，该怎么办？

（学生独立测量和计算图形①、②、③的周长，小组合作测量图形④的周长）

生1：图形①（长方形）、图形②可以直接数方格，数出它们的周长。还可以先数出每条边的长度，再把几条边的长度加起来，算出它们的周长。

生2：先量出图形③（三角形）每条边的长度，再将三条边的长相加，得到它的周长。

生3：无法通过数方格或直接量得图形④的周长，那么可以用绳子绕图形一周，做好标记，再拉直绳子测量，量出的长度就是该图形的周长。

［思考］

此环节通过两个活动帮助学生理解周长的本质。

通过“量（数）与加”求出图形①、②、③的周长，学生从测量单条线段的长度，到计算几条线段的长度之和得到图形的周长，初步感悟到直边图形的周长就是图形所有边的长度之和。

通过“化曲为直”的方法求出图形④的周长，用线绕曲线图形一周，拉直线后测量线的长度。从“封闭图形一周的长度”到“封闭图形的所有边的长度之和”，学生从“累加”的角度出发，对周长概念的理解从一条线的长度扩展到多条线长度之和。

4.辨析周长概念

活动：一分为二。

操作：画一条线把长方形对角的两个顶点连起来，将长方形分成两部分。（提示：越特别越好）

展示：教师在黑板上画出“两部分的周长相等”“两部分的周长不相等”“有疑问”三栏，让学生将自己的作品贴在其中一栏上。

师：将长方形沿对角线分成两部分，得到的图形①和图形②的周长相等吗？

生1：周长相等。因为图形①的两条直角边和图形②的两条直角边分别相等，对角线既是图形①的边也是图形②的边，所以图形①和图形②的周长相等。

师：在长方形中画一条曲线，沿曲线将长方形分成两部分，得到的图形①和图形②的周长相等吗？

生2：图形①的两条直角边和图形②的两条直角边分别相等，这条曲线既是图形①的边也是图形②的边，因此图形①和图形②的周长相等。

师：周长是封闭图形一周的边线的长度之和，如果两个图形对应的边长度都相等，那么它们的周长也相等。

［思考］

学生用线段、任意曲线分别连接长方形对角顶点将其“一分为二”，然后判断分成的两部分图形的周长是否相等。辨析活动中，学生体会到“如果两个图形对应的边长度都相等，那么它们的周长相等”，从而促使学生更灵活地理解一一对应视角下的周长。

笔者从学情调查中确定教学起点，从多版本教材的对比分析中确立教学重心，从课堂实践中探寻教学路径，这一堂课的研究思路，也指引了这一类课的研究路径。