铁路物流实时监控系统中具有消息恢复的身份认证方案
2023-04-07易传佳左黎明陈艺琳
易传佳 左黎明 陈艺琳
(华东交通大学理学院 江西 南昌 330013) (华东交通大学系统工程与密码学研究所 江西 南昌 330013)
0 引 言
随着现代物流业迅猛发展,铁路物流凭借运量大、辐射广、安全可靠等特点成为了现代物流业中的主要方式之一[1]。近年来,铁路交通事故频发,仅2020年,我国已经发生了三起铁路交通事故[2],造成了重大的人员和财产损失。“6·13”温岭槽罐车爆炸事故造成20人死亡,172人受伤[3]。铁路物流要防范上述事故的发生,必须建立有效的智能监控平台,实时保证铁路运输的安全性。依托新兴的大数据、云计算、人工智能等互联网技术,铁路物流实时监控系统的设计已经成为当前的研究热点[4-6]。在复杂的互联网环境下,物流实时监控系统的数据交互过程存在信息泄露和信息篡改的网络安全隐患,这会严重威胁到整个监控系统的稳定运行。物流监控系统存在风险的根本主要在于数据来源缺乏安全性认证,数据传输缺乏完整性保护。针对铁路物流实时监控系统存在的信息安全问题,需要一种高效安全的签名方案来解决。在网络传输带宽受限环境中,具有短的消息签名长度的签名方案很适用。目前缩短签名长度有两种方式:(1) 设计短签名方案,短签名的概念由Boneh等[7]首次提出,在同等安全条件下,其签名长度与DSA签名相比缩短一半;(2) 直接压缩传输的消息,该方法源于Nyberg等[8]首次提出的具有消息恢复功能的签名方案,该方案不需要将消息同签名一起传送给验证者,而是将原始消息嵌入到签名,验证者可以自行从签名中恢复原始消息。本文主要研究第二种具有消息恢复功能的签名方案并应用到铁路物流实时监控系统中。
Shamir[9]在1984年提出了基于身份的密码体制,用户私钥通过一个可信的私钥生成器(Private Key Generator,PKG)利用系统主密钥和用户身份信息生成。Ma[10]构造了一种高效的基于身份的群签名方案。Li[11]提出了一种具有消息恢复的基于身份的强指定验证者签名方案。Rao等[12]针对表达型线性秘密共享方案的可实现访问结构,设计了两个基于密钥策略及属性的具有消息恢复的密钥隔离签名方案。Chande等[13]应用自认证密钥和消息恢复的概念提出了一个有效的多代理签名方案,该方案可以同时执行公钥验证、多代理签名验证和消息恢复。Verma等[14]给出了一种可证明安全的、高效的基于身份的消息恢复盲签名方案。James等[15]利用盲签名和消息恢复特性,提出了一种基于身份的具有消息恢复的无配对盲签名方案。阚元平[16]在格密码基础上提出了一种具有消息恢复功能的身份签名方案,该方案能够抵抗伪造攻击。针对铁路物流实时监控系统存在的信息安全问题,本文提出一种高效的基于身份的带消息恢复功能的签名方案,并以该签名方案为核心设计一种身份认证方案,整个方案交互过程计算量小、数据传输少,可以有效保障物流监控系统数据来源的可靠性和安全性。
1 基础知识
1.1 物流实时监控系统设计
物流实时监控系统整体架构如图1所示,主要由电子标签、数据采集装置和云服务平台三部分组成。
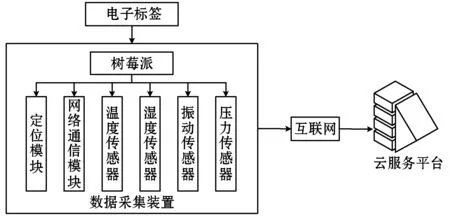
图1 整体架构
电子标签内嵌有密码芯片,数据采集装置以树莓派为控制中心,通过传感器实时采集当前的数据,并通过网络通信模块实现与云服务平台的通信。数据采集装置中传感器包括定位模块、温度传感器、湿度传感器、振动传感器、压力传感器。
在该物流实时监控系统中,货物封箱完毕后,电子标签粘贴于货物的启封处,当电子标签激活后,如果没有收到云服务平台的授权,电子标签的损坏将会导致数据采集装置向云服务平台发送警告信息。在物流过程中,数据采集装置通过传感器实时采集货物当前的状态数据并传输到电子标签中,然后电子标签对状态数据进行数字签名,再由数据采集装置将签名信息发送给云服务平台,云服务平台接收签名信息并验证签名,签证成功后恢复数据信息,然后将数据保存在云服务器中。
1.2 基于身份具有消息恢复功能的签名方案
基于身份的具有消息恢复功能的签名方案[17]由系统初始化、私钥解析、签名和验证签名四个算法组成,具体描述如下:
1) 系统初始化:给定安全参数,输出系统参数和主密钥,PKG秘密保存主密钥,公开系统参数。
2) 私钥解析:输入用户身份ID,计算用户私钥,并通过一个安全的通道发送给用户。
3) 签名:输入系统参数、身份ID和用户私钥,输出签名,并发给验证者。
4) 验证签名:输入系统参数、签名,输出验证结果:“TRUE”或者“FALSE”,输出恢复的完整消息。
在物流实时监控系统中,云服务平台中有私钥生成器(PKG),每个电子标签有唯一的ID,PKG通过电子标签ID生成签名私钥,在电子标签初始化时,向电子标签内注入系统参数以及PKG生成的私钥。当云服务器对签名信息进行验证时,验证成功则输出恢复的完整消息,验证失败则发出警告信息。
2 签名方案构造
基于椭圆曲线上离散对数问题的难解性,提出一种基于身份的具有消息恢复功能的签名方案。
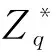
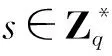
H3:{0,1}*×G×G→{0,1}l1+l2,
F1:{0,1}l1→{0,1}l2,
F2:{0,1}l2→{0,1}l1。
最后PKG掌握并保密系统主密钥s,公开系统参数params={q,P,e,Ppub,H1,H2,H3,F1,F2,l1,l2}。
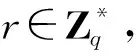
3) 签名:对任意给定的消息m∈{0,1}l1进行签名,过程如下:
T=tP
(1)
h2=H2(ID,R,T)
(2)
u=t+xIDh2
(3)
(2) 计算:
h3=H3(ID,R,uP)∈{0,1}l1+l2
(4)
h4=F1(m)‖(F2(F1(m))⊕m)∈{0,1}l1+l2
(5)
h=h3⊕h4
(6)
则σ=(h,T)为电子标签对消息m的签名。
4) 签名验证:对给定消息m的签名σ=(h,T),云服务端可以验证签名合法性并恢复出原始消息,验证过程如下:
(1) 依次计算:
h1=H1(ID)
(7)
h2=H2(ID,R,T)
(8)
h3=H3(ID,R,T+h2R+h1h2Ppub)
(9)
(2) 计算h4=h3⊕h,从h4的二进制串表示中分离出长度为l2的串f1和长度为l1的串f2,恢复消息m′=F2(f1)⊕f2。
(3) 验证等式f1=F1(m′)是否成立,若成立则接受签名σ=(h,T)为合法签名,并输出1,否则输出0。正确情况下f1=F1(m)和f2=(F2(F1(m))⊕m),因此我们不难看出消息恢复过程的正确性。
整个签名验证和消息恢复过程正确性证明如下:
h3=H3(ID,R,uP)=
H3(ID,R,(t+(r+sh1)h2)P)=
H3(ID,R,(t+xIDh2)P)=
H3(ID,R,T+h2R+h1h2Ppub)
(10)
h4=h3⊕h
(11)
由于:
h4=F1(m)‖(F2(F1(m))⊕m)
(12)
f1=F1(m)
(13)
f2=(F2(F1(m))⊕m)
(14)
可得:
m′=F2(f1)⊕f2=
(F2(F1(m)))⊕(F2(F1(m))⊕m=m
(15)
3 具有消息恢复的身份认证方案设计
图2为具有消息恢复的身份认证方案数据交互原理图,其中:Sign表示签名;Verify表示验证签名。方案具体的交互流程如下:
(1) 数据采集端采集数据。数据采集端通过传感器采集实时数据data,然后将实时数据data传输到电子标签。
(2) 电子标签生成签名。电子标签接收数据采集端传输的数据data后,然后调用签名算法对data进行签名处理,最后电子标签将签名结果和电子标签ID以ID#Sig的封包格式传输到数据采集端。
(3) 数据采集端将签名结果传输到服务端。数据采集端将ID与签名结果以ID#Sig的封包格式通过网络通信模块传输到服务端。
(4) 服务端身份验证。服务端接收数据采集端传输的消息封包后,对消息封包解析,得到ID和Sig,通过ID检索对应的主公钥Ppub对签名进行验证,如果验证成功,恢复出消息得到data并保存到云服务器中,如果验证失败则提示异常警告。
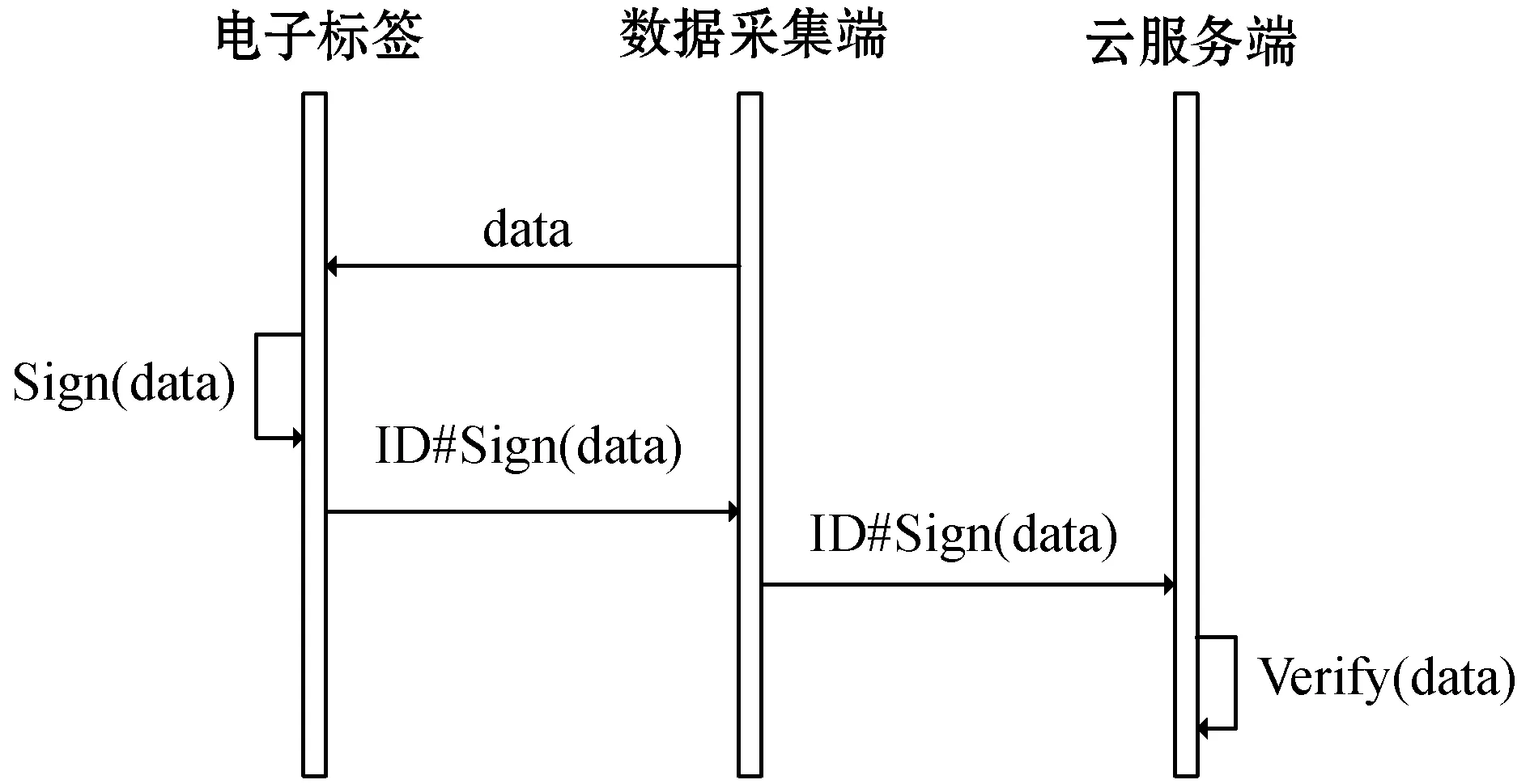
图2 数据交互
4 方案实现与效率分析
4.1 方案实现
在Windows 7 64位操作系统Microsoft Visual Studio 2012微软平台下,采用C#轻量级密码术包(bouncy castle)实现了本文方案,实验结果显示本方案签名所消耗时间为0.057 s,验证所消耗时间为0.054 s,表明该签名方案效率较高。实现结果如图3所示,核心代码如下:
//签名算法
BigInteger t=new BigInteger("8");
//计算T=tP
ECPoint T=myecc.ecc_point_g.Multiply(t);
string RR=R.X.ToBigInteger().ToString()+
R.Y.ToBigInteger().ToString();
string TT=T.X.ToBigInteger().ToString()+
T.Y.ToBigInteger().ToString();
string IDRT=ID+RR+TT;
BigInteger uu=new BigInteger(
myhash.TanGetDigestByteArray(IDRT));
//计算u=H2(ID,R,T)
BigInteger u=uu.Mod(myecc.ecc_n);
//计算U=t+xID*u
BigInteger U=
t.Add(xID.Multiply(u)).Mod(myecc.ecc_n);
ECPoint UP=myecc.ecc_point_g.Multiply(U);
string strUP=UP.X.ToBigInteger().ToString()+
UP.Y.ToBigInteger().ToString();
string IDRUP=ID+RR+strUP;
//计算h1=H3(ID,R,UP)
byte[]h_1=
myhash.TanGetDigestByteArray(IDRUP);
byte[]h1=new byte[64];
Array.Copy(h_1,0,h1,0,32);
Array.Copy(h_1,0,h1,32,32);
//计算h2
byte[]F1=myhash.TanGetDigestByteArray(m);
byte[]F2=myhash.TanGetDigestByteArray(F1);
byte[]F2Xorm=HexXorByte(F2,m);
byte[]h2=new byte[64];
Array.Copy(F1,0,h2,0,32);
Array.Copy(F2Xorm,0,h2,32,32);
//计算h等于h1与h2的“异或”
byte[]h=HexXorByte(h1,h2);
//(4)签名验证
//计算R+l*Pub
ECPoint TRu=T.Add(xID_rignt.Multiply(u));
string TRu_xy=TRu.X.ToBigInteger().ToString()+
TRu.Y.ToBigInteger().ToString();
string IDRTRu=ID+RR+TRu_xy;
//计算h1=H3(ID,R,T+(R+l*Pub)u)
byte[]h1_1=
myhash.TanGetDigestByteArray(IDRTRu);
byte[]h11=new byte[64];
Array.Copy(h1_1,0,h11,0,32);
Array.Copy(h1_1,0,h11,32,32);
//计算h2=h与h1的“异或”
byte[]h21=HexXorByte(h,h11);
byte[]h21l2=new byte[32];
byte[]h21l1=new byte[32];
//截取h2的前l1长度的字节
Array.Copy(h21,0,h21l2,0,32);
//截取h2的后l2长度的字节
Array.Copy(h21,32,h21l1,0,32);
byte[]F21=myhash.TanGetDigestByteArray(h21l2);
//恢复消息m
byte[]m1=HexXorByte(h21l1,F21);
//消息恢复比较
byte[]left=myhash.TanGetDigestByteArray(m1);
byte[]right=h21l2;
if (ByteEquals(left,right)){
Console.WriteLine("消息恢复成功,签名验证通过!");
}
else{
Console.WriteLine("消息恢复失败,签名验证失败!");
}
Console.WriteLine("原消息:{0}",msg);
Console.WriteLine("恢复的消息:{0}",
Encoding.UTF8.GetString(m1));
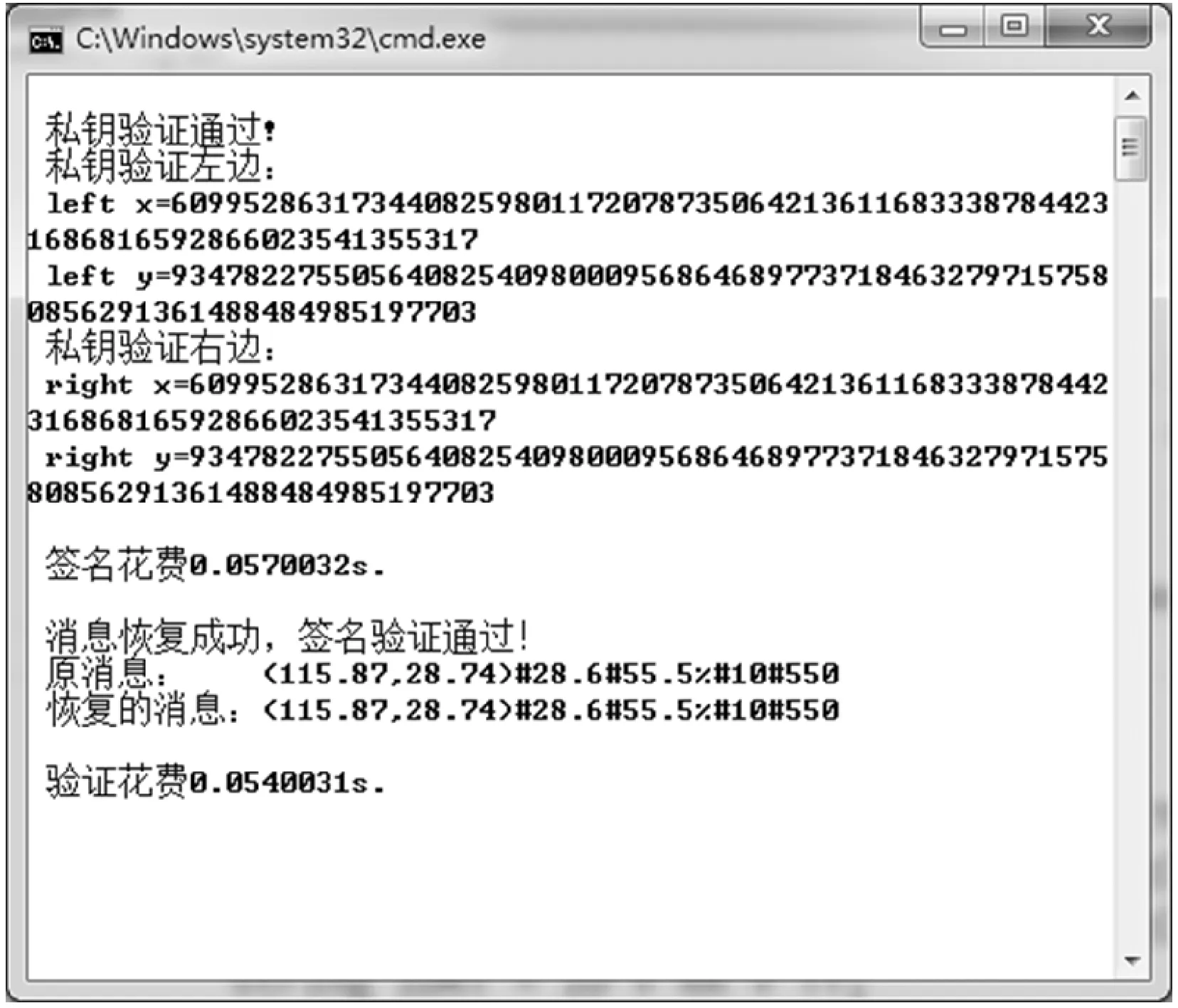
图3 方案实现结果
4.2 效率分析
表1为本文方案与其他基于身份的签名方案的性能比较,其中:M表示标量乘运算;P表示双线性对运算;E表示指数运算;|G1|是G1中的元素长度;|q|是Zq中元素的长度;n是一个常数;“√”表示具有可恢复消息功能;“×”表示不具有可恢复消息功能。
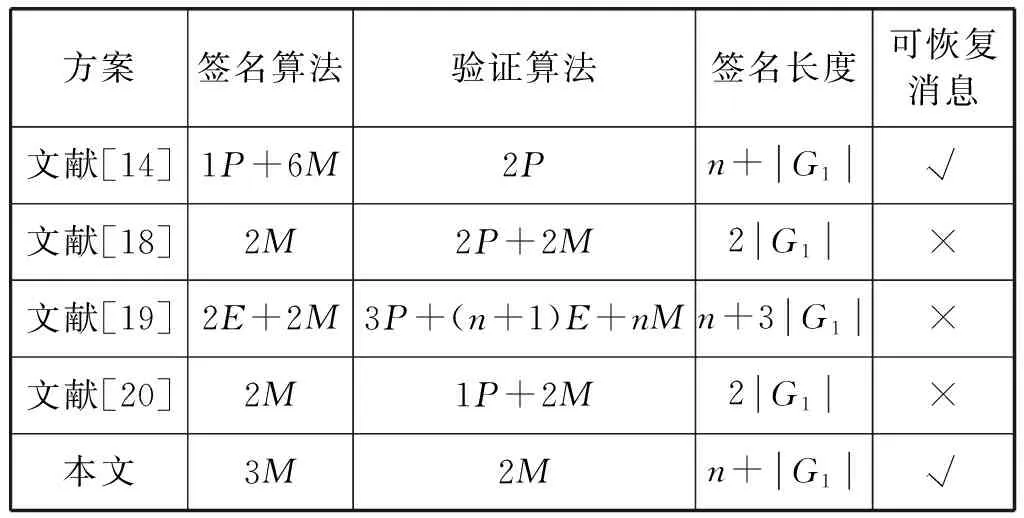
表1 本文方案与现有方案性能比较
由表1可得,与其他方案相比,本文方案签名长度是最短的,与文献[14]方案接近。在计算量方面,文献[14]使用了3次双线性运算,文献[18]使用了2次双线性运算,文献[19]使用了3次双线性运算,文献[20]使用了1次双线性运算,本文方案没有使用双线性运算,由于双线性对的计算消耗是最大的,因此本文方案相比其他签名方案计算量较小,所需的传输带宽更低、性能更优、运算效率更高。
5 结 语
针对铁路物流实时监控系统存在的信息安全问题,本文结合基于身份密码体制和消息恢复功能,提出基于身份具有消息恢复功能的签名方案。并以此方案为基础,设计一种铁路物流实时监控系统中具有消息恢复的身份认证方案。使用C#语言版轻量级密码包对方案进行实验仿真,与几种基于身份的签名方案进行了效率比较。该方案可以减少通信量、降低通信代价,能很好地用于铁路物流实时监控系统中。
