针对大规模数据的随机权值前馈神经网络模型优化

黄婷婷 冯 锋

(宁夏大学信息工程学院 宁夏 银川 750021)

0 引 言

近年来,前馈神经网络(FNNs)以其结构的灵活性和良好的表示能力而受到越来越多的关注。前馈神经网络(FNNs)具有自适应特性和普遍逼近特性,在回归和分类中得到了广泛的应用,同时为大量的自然和人为现象提供了研究模型,已经应用于科学研究和工程的各个领域。在传统的神经网络理论中,FNNs的所有参数,例如输入权值、偏置和输出权值都需要在特定的情况下进行调整,但由于网络结构的层次性,这一过程复杂并且低效。通常采用基于梯度的优化方法,如反向传播(BP)算法,但是这种方法通常存在局部极小值、收敛速度慢和学习速度敏感等问题。此外,一些参数,如隐藏节点的数量或学习算法参数,必须手动调整[1-6]。针对这一系列的问题,具有随机权值的前馈神经网络(FNNRWs)应运而生。FNNRWs是Schmidt等[7]在1992首次提出的,其中输入权值和偏置随机分配,均匀分布在[-1,1]中,输出权值可以用著名的最小二乘法进行分析确定。许多文献的仿真研究表明,随机化模型与完全适应模型相比具有较高的性能,提供了更简单的实现和更快的训练速度。

从理论上讲,输入权值和偏置的随机分配很明显不能保证全局的逼近能力[8-9]。针对各种各样的侧重点,随机学习算法层出不穷。例如,文献[3]提出了一种具有随机权值的前馈神经网络迭代学习算法;文献[6]对随机权重网络的稀疏算法及随机单隐层前馈神经网络元启发式优化进行了研究;文献[9]为了确保普遍逼近性质,针对随机权值和偏置的约束,推动了神经网络随机化方法的发展;文献[10]对随机向量函数链网络的分布式学习进行了研究;文献[11]提出了一种利用随机权值神经网络进行鲁棒建模的概率学习算法。此外,文献[12]对于神经网络的随机化方法进行了完整的论述。但是,随着信息技术的不断发展,数据处在一个爆炸增长的阶段。随之而来的问题就是NNRWs模型中数据样本或神经网络隐含层节点的数量变得非常大,从而计算输出权值的方法非常耗时。针对这个问题,在过去的几十年里,也有很多关于大规模数据建模问题的研究。文献[13]描述了如何在大数据集上有效地训练基于神经网络的语言模型;文献[14]介绍了一个用于大规模数据建模和分类的节能框架;文献[15]分析了一种便于神经网络大规模建模的种群密度方法;文献[16]提出了一种用于大规模神经网络训练的并行计算平台;文献[17]介绍了一种用于大规模神经网络仿真的多处理机结构。其中处理大规模数据集的最简单的策略可能是通过子抽样减少数据集的大小。这种分解方法首先是由Osuna等[18-19]提出的,Lu等[20]也提出过该方法,用于解决模式分类问题。不过本文所采用的对于大规模数据处理的方法与文献[21-22]提出的贝叶斯委员会支持向量机(Bayesian committee SVM)处理大规模数据的方法类似。这种方法是将数据集划分为大小相同的子集,并从各个子集派生出一些模型,各个子模型单独训练,最后进行汇总得出最终的结论。

本文针对大规模数据集,研究了基于分解技术的具有随机权值的前馈神经网络模型。本文主要采用的方法就是将样本随机地分为大小相同的小子集,每个子集派生出相对应的子模型。在具有随机权值的前馈神经网络中,决定非线性特征映射的隐藏节点的权值和偏差是随机设置的,不需要学习。选择适当的区间来选择权重和偏差是非常重要的。这个话题在很多文献中还没有得到充分的探讨。本文所采用的方法根据激活函数计算出最优的输入权值和偏置的取值范围,每个子模型在该最优取值范围内初始化相同的输入权值和阈值,同时采用迭代的方案对输出权值进行评估。

1 传统的具有随机权值的前馈神经网络学习算法

前馈神经网络在很多领域都有广泛的应用,单隐层前馈神经网络一般描述为:

(1)

式中:x=[x1,x2,…,xn]T∈Rn表示输入;ωi=[ωi1,ωi2,…,ωin]∈Rn表示输入权重;bi∈Rn是偏置;g(·)表示激活函数,激活函数一般采用比较常见的Sigmoid函数,如式(2)所示;βi∈R表示输出权重。前馈神经网络神经元的数学模型如图1所示。

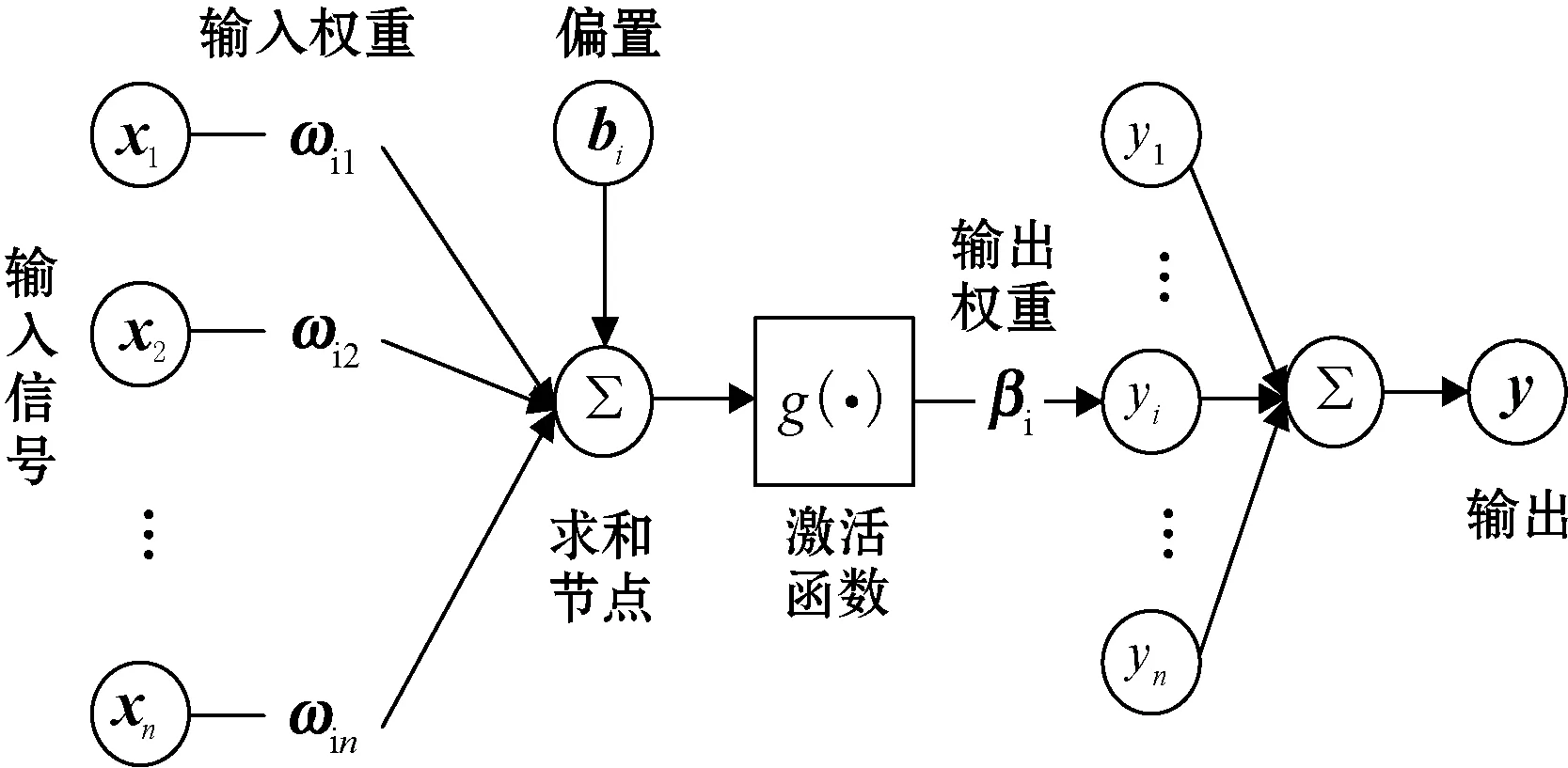
图1 前馈神经网络神经元的数学模型

s={(xj,tj):xj∈Rn,tj∈R,j=1,2,…,M}为训练样本,针对该训练样本有Hβ=T,其中:β=[β1,β2,…,βN]T是输出权重;T=[t1,t2,…,tM]T是目标输出。并且:

一般情况下,输入权值和偏置都是随机分配的,并且ωi～U(ωmin,ωmax),bi～U(bmin,bmax),输出权值可以通过著名的最小二乘法来确定。

式中:β=(HTH)-1HTT。但最小二乘问题一般是不适定的,可以使用L2正则化方法来解决这类问题:

式中:μ>0是一个正则化因子。如果HTH+μI是可逆的,则式(5)可以写成:

β=(HTH+μI)-1HTT

(6)

式中:I表示单位矩阵。

2 改进的具有随机权值的前馈神经网络学习算法

针对大规模数据,将样本随机分为m个部分,s={s1,s2,…,sm},对于每一个子集si派生出相对应的子模型,初始化相同的输入权值和偏置,计算隐含层输出矩阵Hsi,并且使Hsi为正定矩阵。同时,在初始化子模型的过程中,每个子模型的隐含层输出矩阵Hsi和目标输出Tsi等相关的参数会确定下来,在后期计算过程中不再发生改变。整体结构如图2所示。

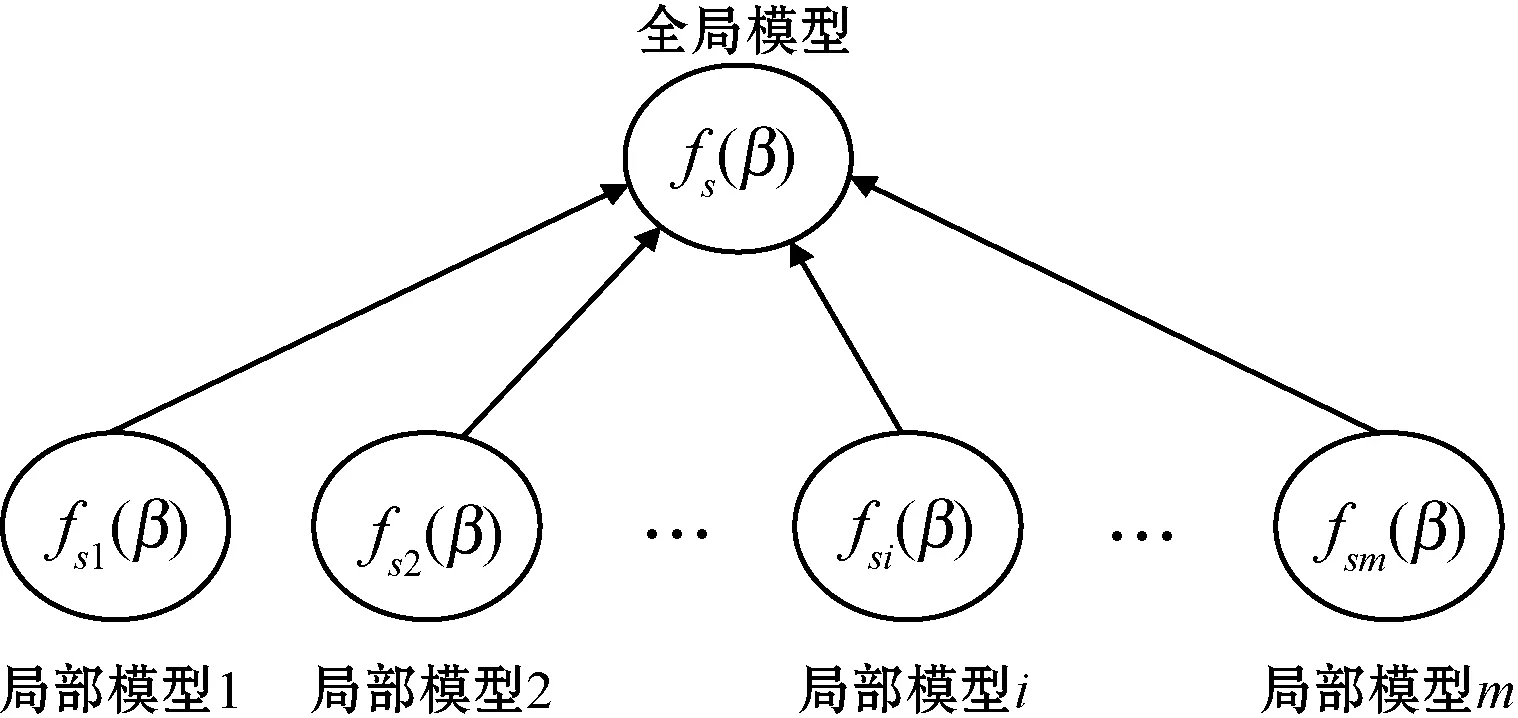
图2 整体结构

在本文算法中,激活函数使用最常见的Sigmoid函数,为方便起见,激活函数可以记为:

式中:参数ω是输入权值,参数b是偏置,根据式(7)可以看出参数b控制g(x)的图像在x轴上的移动。对激活函数求导如式(8)所示,可以看出当ω>0时,导数也大于零,也就是激活函数g(x)的斜率大于零;同理,当ω<0时,激活函数g(x)的斜率也小于零,所以可以将ω作为g(x)的斜率参数。由图3可知,当x=0时,g(x)=0.5;x=1时,假设g(x)=r。当r=0.5时,g(x)是最平坦的;当r=0时,g(x)是最陡峭的。可以看出,r控制了激活函数g(x)的陡峭程度。

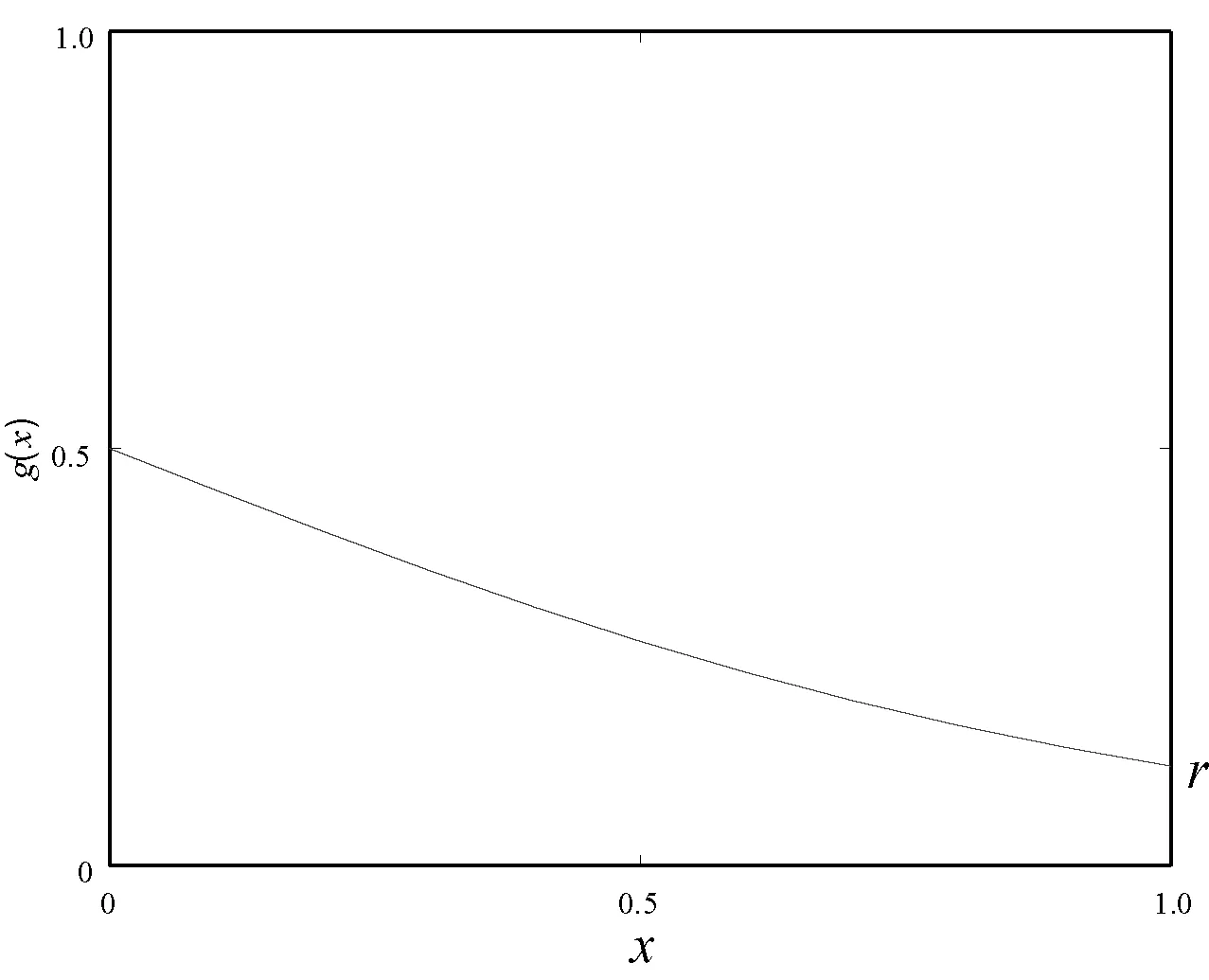
图3 激活函数中最平坦的部分

当x=1时,g(x)=r,当偏置b=0时,可以得到:

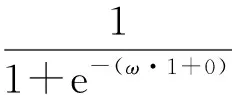
(9)

通过式(9)得到:

从激活函数的图像中可以看出,图像中最平坦的区间在x=1周围,则:

ω≤-|ω1|或者ω≥|ω1|

(11)

为了更准确地确定参数的范围,令ω2=s·ω1,其中参数s>1,用来定义最大的输入权值,也就是激活函数中最陡的部分,则:

ωi∈[-|ω2|,-|ω1|]∪[|ω1|,|ω2|]

(12)

从而得到:

式中:参数s决定了激活函数中最陡的部分,其具体取值通过目标函数来确定。

对于参数b的确定,当x∈[0,1]时,根据图3可以得到:

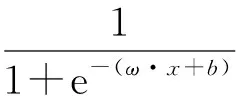
(14)

从而可以得到:

b=-ω·x

(15)

对于x=0,可以得到b的第一个边界b1=0;对于x=1,可以得到b的第二个边界b2=-ω。可以看出,偏置b是依赖于输入权重ω的,从而可以得到偏置b的范围为:

在输入权值ω和偏置b的随机确定过程中,最优的确定范围如式(16)所示。

在输出权值的确定过程中,随机初始化输出矩阵为β(0),分别计算局部梯度为:

和全局梯度:

同时计算出:

式中:Tsi是第i个局部模型的目标输出。

在进行每次迭代运算时对每个局部模型进行优化:

(20)

为了更好地理解这个局部模型,引入Bregman散度:

Bψ(β,β′)=ψ(β)-ψ(β′)-▽ψ(β′)·(β-β′)

(21)

在本算法中,对于每个fsi(β),有:

式中:σ是正则化参数。其对应的Bregman散度为:

(23)

根据式(23),式(20)可以转化为:

与此同时,根据泰勒展开式,Bregman散度转化为:

(β-β(t-1))

(25)

从而,式(20)可以更进一步转化为:

由上述推导,可以得到最终的输出权值为:

▽fs(β(t-1))

(27)

3 实验与结果分析

本节对本文算法的性能进行了验证,所有实验均在MATLAB 7.10.0 (2010a)环境下进行,运行奔腾(R)双核E5400处理器,速度2.70 GHz,内存2 GB。算法使用的激活函数是Sigmoid函数g(x)=1/(1+e-x)。由于是针对大规模数据的处理,因此,本文采用的数据集是UCI标准数据集中的Statlog数据集、Bank Marketing数据集和Letter Recognition数据集。为验证算法的有效性,首先将样本分为m个相等的子集,并对所有样本进行归一化处理。在实验过程中,在计算输入权重和阈值的过程中选用的参数r=0.1、s=3。采用的正则化参数σ=0.05、学习速率η=10-3、阈值ε=10-3。

表1-表3分别展示了当子集个数m=15时的Statlog数据集、子集个数m=15时的Bank Marketing数据集和子集个数m=10时的Letter Recognition数据集的FNNRWs学习算法和优化后的FNNRWs学习算法的精确度对比。可以看出,随着样本的大小或者隐含层节点数量的增大,优化后的FNNRWs学习算法的精确度高于FNNRWs学习算法的精确度。图4、图5和图6从折线图的角度更直观地展示了优化后的FNNRWs学习算法的精确度和FNNRWs学习算法的精确度随着隐含层节点数量的增大,其训练精度和测试精度的对比,可以非常直观地看到优化后的FNNRWs学习算法在精确度方面的优势。图7通过计算相对误差,从相对误差方面展示了优化后的FNNRWs学习算法在三个数据集上的性能优势。

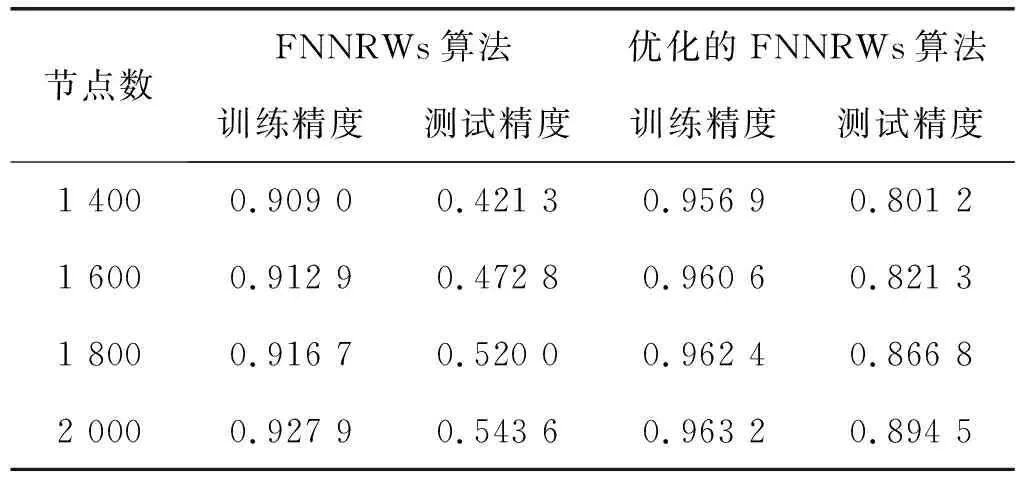
表1 算法在Statlog数据集上的精度

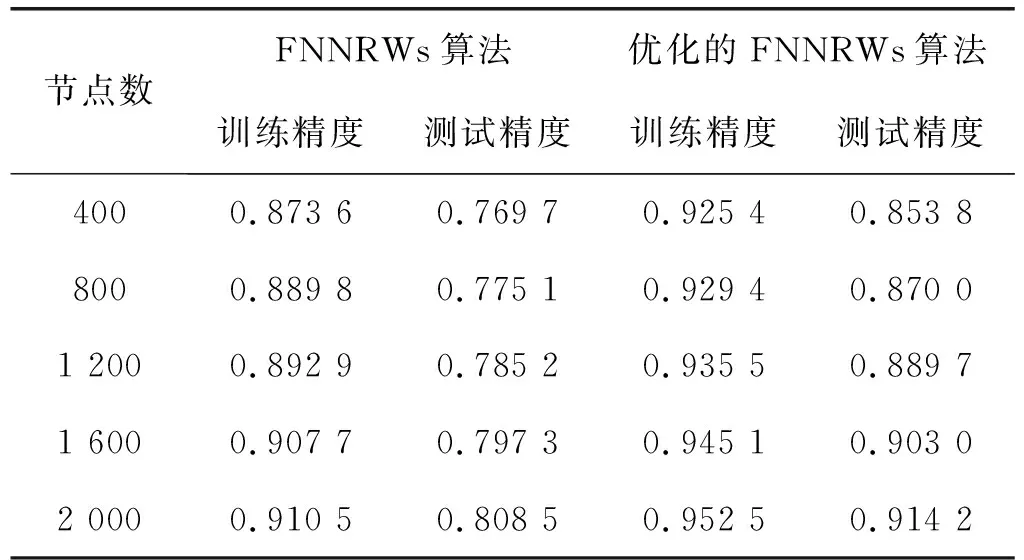
表2 算法在Bank Marketing数据集上的精度

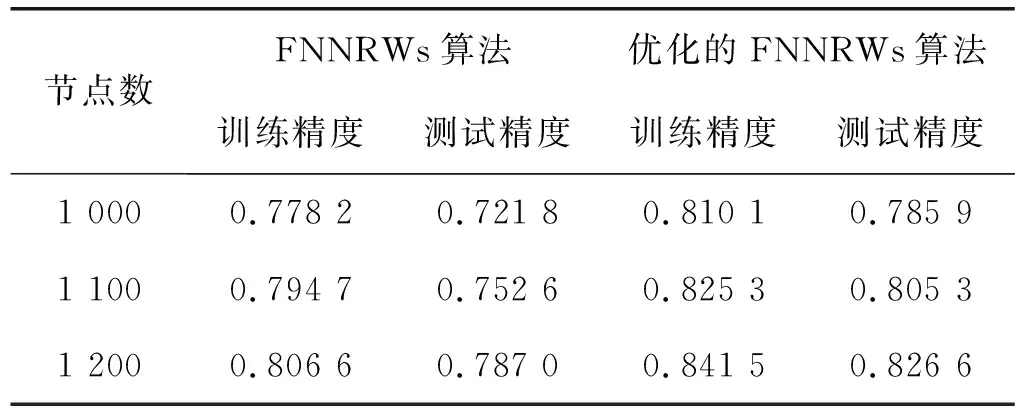
表3 算法在Letter Recognition数据集上的精度

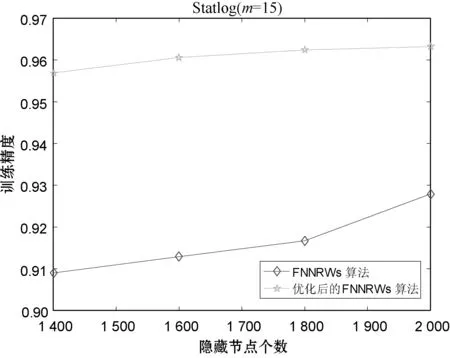
(a)

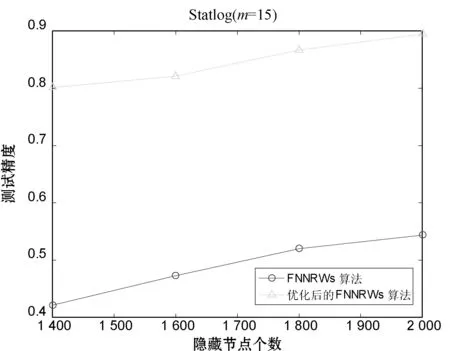
(b)图4 算法在Statlog数据集的训练精确度和测试精确度对比

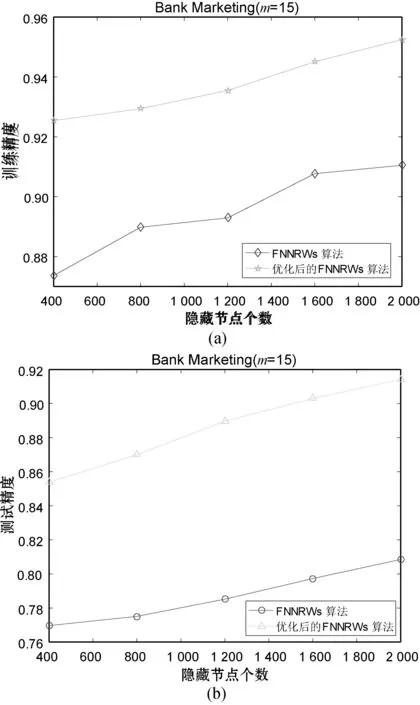
图5 算法在Bank Marketing数据集的训练精确 度和测试精确度对比

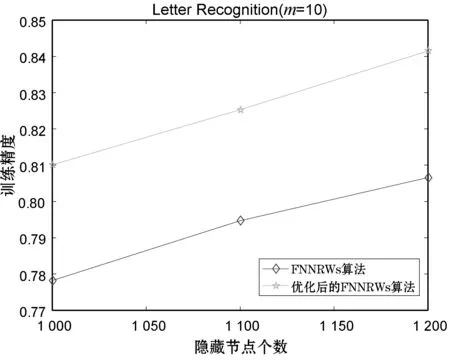
(a)

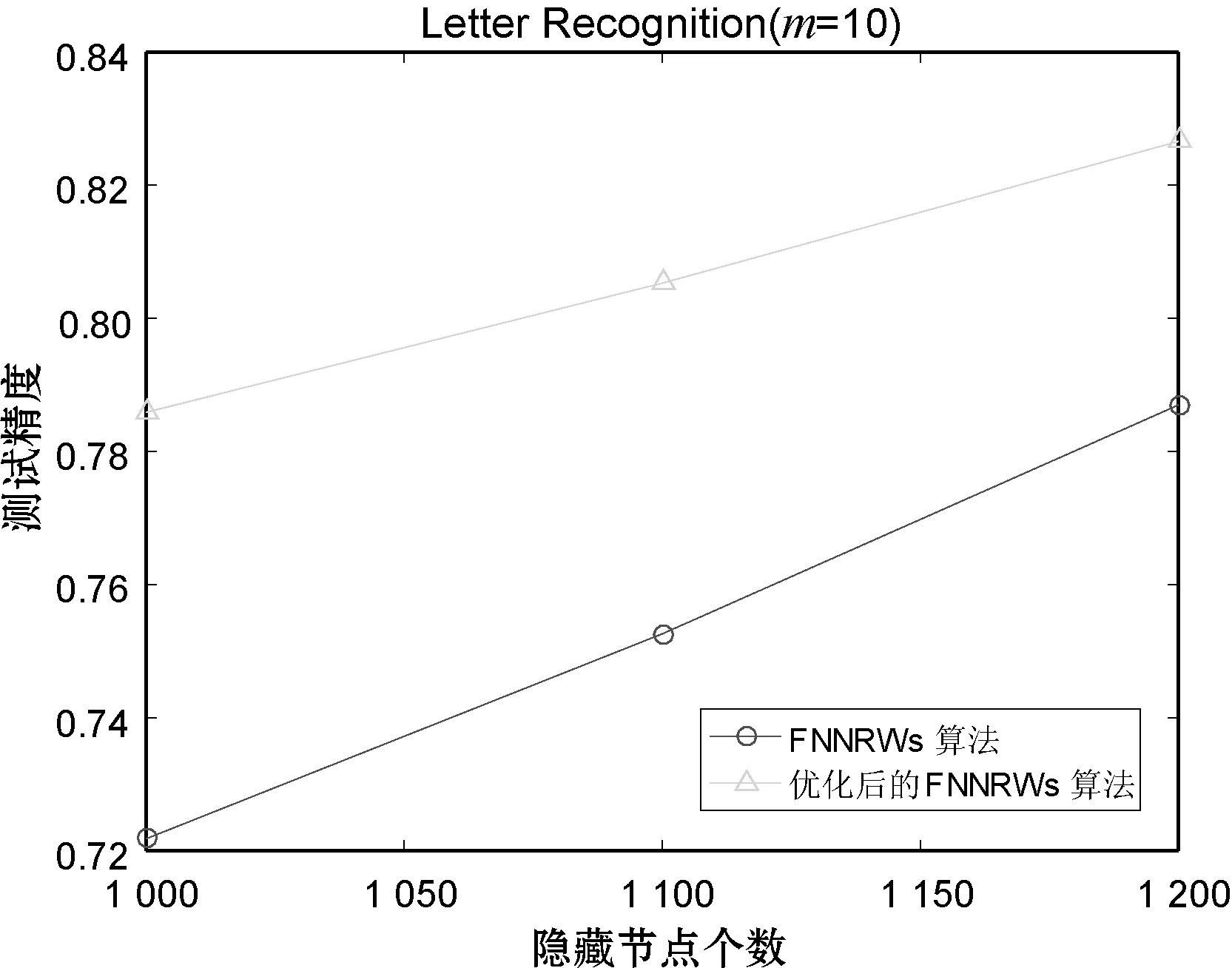
(b)图6 算法在Letter Recognition数据集的训练精确 度和测试精确度对比

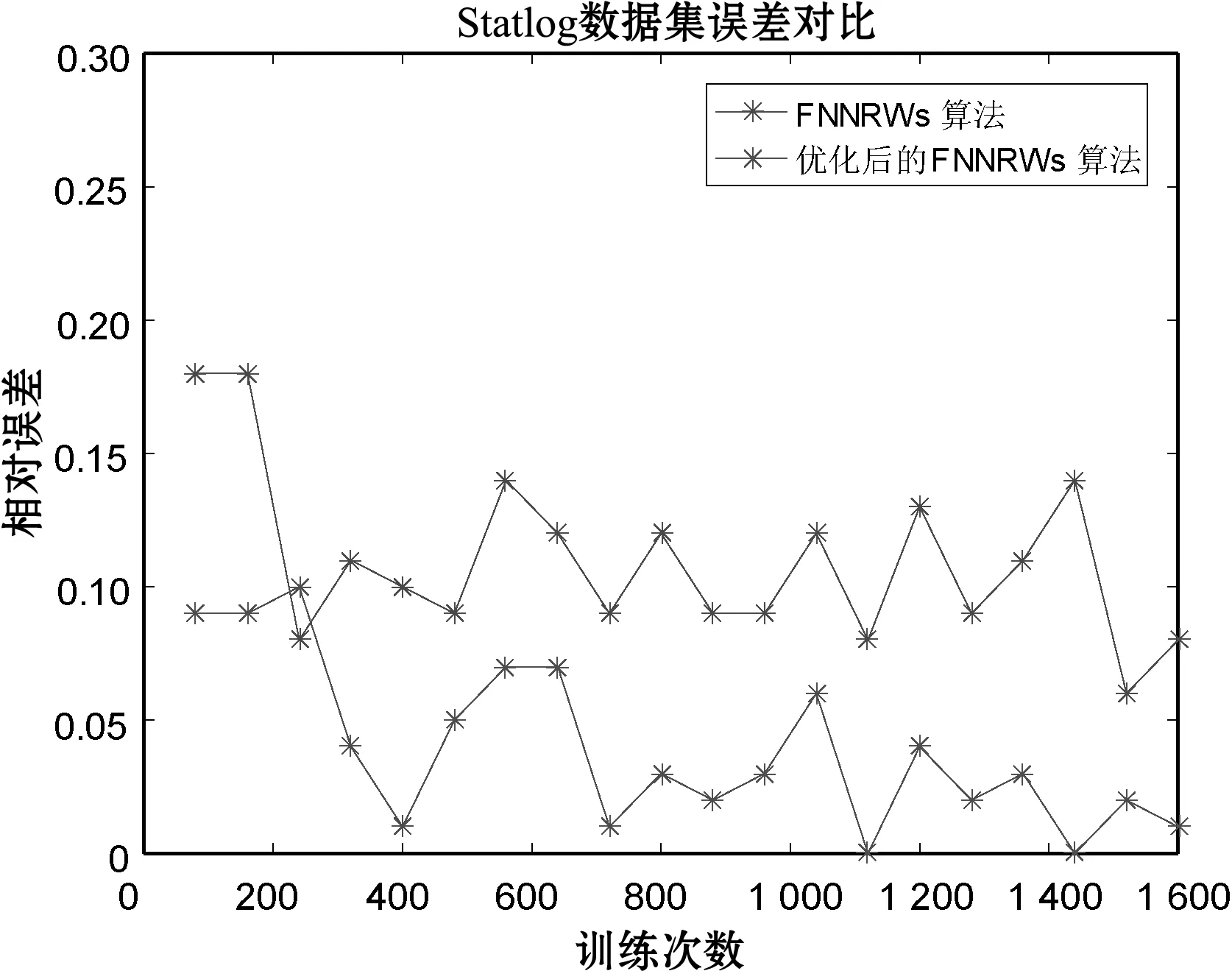
(a) Statlog数据集

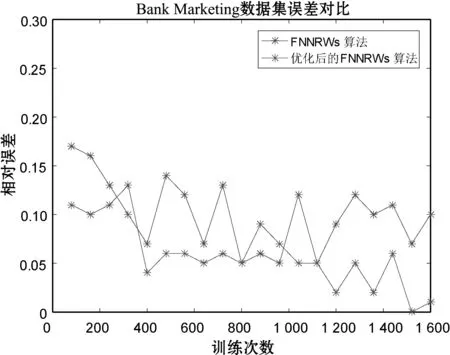
(b) Bank Marketing数据集

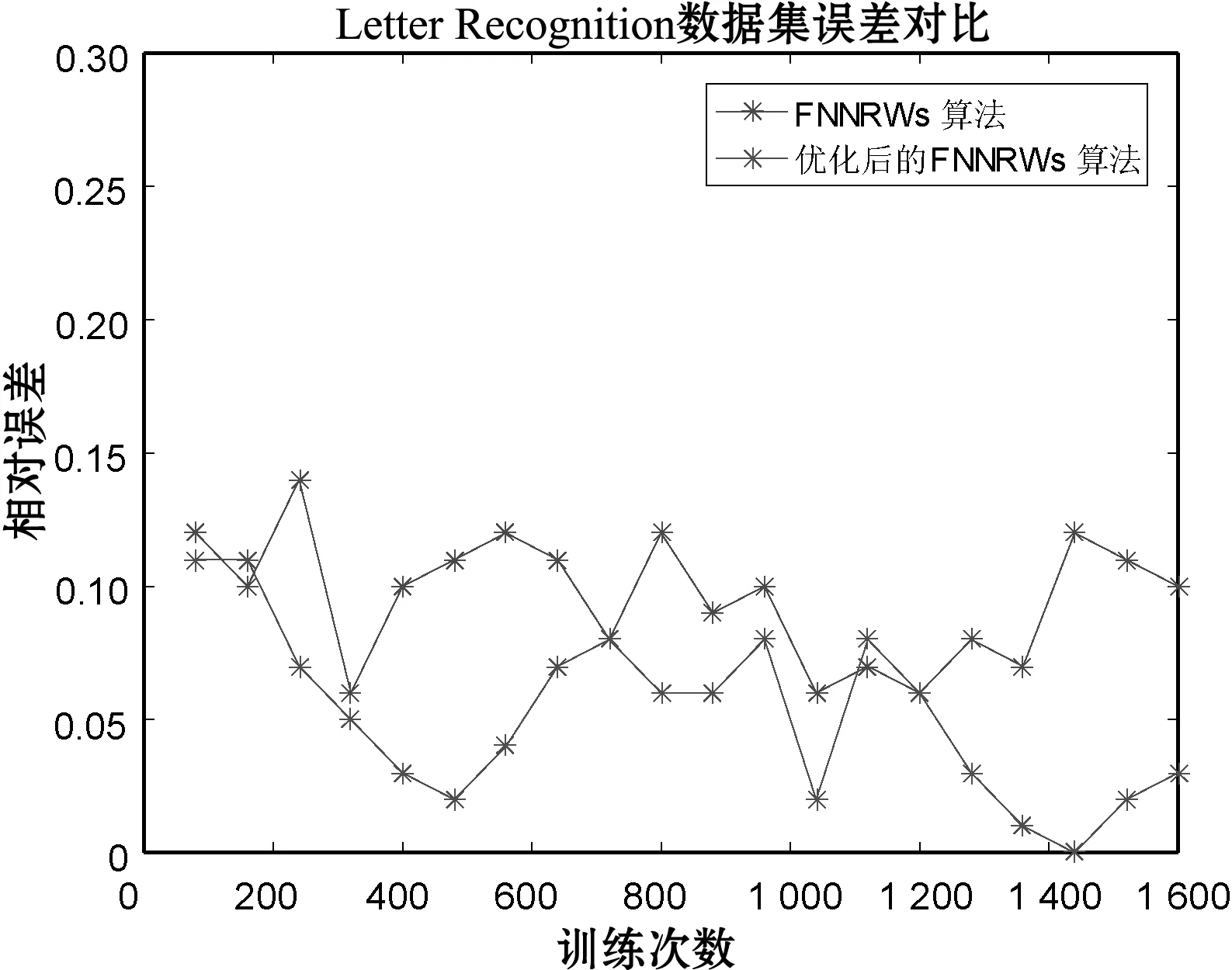
(c) Letter Recognition数据集图7 算法的误差对比

4 结 语

本文在具有随机权值的前馈神经网络(FNNRWs)的基础之上,针对大规模数据集,研究基于分解技术的具有随机权值的前馈神经网络模型。将样本分为大小相同的子集,每个子集派生出相应的子模型。本文主要是通过对于三个参数的产生方法的优化来提高整体的性能。在具有随机权值的前馈神经网络中,输入权值和偏置是随机设置的,不需要学习,选择适当的区间是非常重要的。本文根据激活函数计算出最优取值范围,从输入权值和偏置的取值范围入手,提高整体性能。同时采用迭代方案克服随机模型输出权重评估的困难。在UCI标准数据集上进行了实验,实验结果表明了该算法的有效性。