基于BWDSP1042的复数矩阵向量乘的优化与实现
2023-04-07蔺丽华张美春王佳仪
蔺丽华 张美春 王佳仪 李 敏 门 浩
1(西安科技大学通信与信息工程学院 陕西 西安 710054) 2(西安电子科技大学电子工程学院 陕西 西安 710071)
0 引 言
矩阵向量乘在视频图像处理、无线通信、数学信号处理等领域应用广泛。由于矩阵向量乘计算复杂度较高,运算过程效率低,导致其在一些领域中无法满足系统实时处理的要求[1-2]。因此,提高矩阵向量乘的运算速度是十分必要的。目前,针对矩阵向量乘的研究已经十分成熟,但如何使之适应新的数字信号处理器以获得更好的性能,是目前研究的重点。
针对如何高效实现矩阵向量乘,国内外做了大量研究,肖汉等[3]通过将矩阵向量乘分解成若干个子任务来提高运行速度。尹孟嘉等[4]通过构建性能度量模型为不同形态的矩阵选择不同的存储格式来提高算法的性能。苏锦柱等[5]提出了一种基于FPGA的矩阵向量乘新的并行算法。以上的矩阵向量乘实现方法是针对稀疏矩阵向量乘,不具有普遍性。另外,与FPGA相比,DSP具有较高的运算能力,能够实现实时处理,具有软件的灵活性,且成本相对较低,在BWDSP1042上研究矩阵向量乘具有重要意义。
本文研究了复数矩阵向量乘在BWDSP1042处理器上的优化和实现。根据该处理器的VLIW和SIMD硬件结构,使用软件流水、循环展开、指令并行的手段,结合线性寻址和模八寻址的寻址方式,针对不同矩阵,提出两种不同的优化方法以提高复数矩阵向量乘的运行效率。方法一:按列分块与减少二级循环内循环次数相结合的方法矩阵列非4的倍数)。方法二:模八寻址和减少二级循环内循环次数相结合的方法(矩阵列为4的倍数)。实验结果表明:这两种方法能够有效减少矩阵向量乘的运行周期,充分挖掘了BWDSP1042处理器的潜能。
1 BWDSP1042处理器
BWDSP1042是中国电子科技集团公司第38研究所研制的首款多核处理器。其内部集成2个新一代处理器核eC104+[6]。eC104+采用16发射、单指令流,多数据流架构,其处理性能与BWDSP100相比得到大幅提升。
eC104+中有四个执行宏(x、y、z、t),每个执行宏中存在一个寄存器组和四个运算部件[7],其中运算部件包括一个超算器(SPU)、四个移位器(SHF)、八个乘法器(MUL)、八个算数逻辑单元(ALU)。eC104+的指令总线位宽是512位,包含两条写总线和两条读总线,且每条总线的位宽是256位。数据总线是全双工,因此最多可同时使用三条数据总线实现数据传输。eC104+有6个大小为256k×32 bit的内存块(block),每个内存块中包含八个bank。内部有三个相互独立且结构相同的地址发生器。eC104+内核的结构如图1所示。

图1 eC104+内核的结构
eC104+内核是13级流水线结构,可分为三部分,分别为由内存驱动的取指令3级(fe0~fe2)、指令缓冲3级(IAB0~IAB2)、由指令驱动的7级流水(指令译码4级(dc1~dc4),取操作数1级(ac),指令执行1级(ex),指令结果写回1级(wb))。如图2所示,在水线的dc~wb级有很多因素会引起指令流水的停顿,主要因素包括数据bank冲突、数据相关、原子操作、分支、访问核外存储资源引发的等待、异常及程序控制指令等。
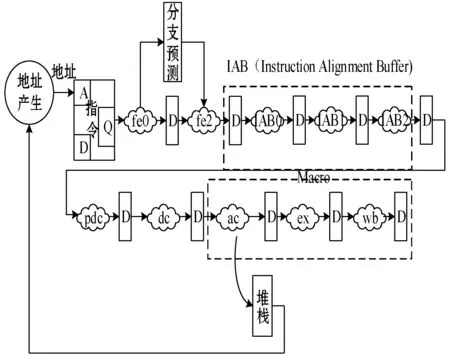
图2 eC104+内核的13流水线结构
2 复数矩阵向量乘算法
传统的复数矩阵向量乘由一个二级循环实现,即复数矩阵A中的第t行与向量x中各个元素相乘、累加,完成yt的计算。具体过程如下所示:
复数矩阵:
式中:i表示虚部,r表示实部,m表示行,n表示列。
n维的复数向量:
x=(xi1+xr1,xi2+xr2,…,xin+xrn)T
(2)
A与x相乘得复数向量y:
y=(yi1+yr1,yi2+yr2,…,yim+yrm)T
(3)
任意yt满足式:
该传统运算方法,在BWDSP1042上实现具有运算效率低的问题。
3 复数矩阵-向量乘算法的优化与实现
3.1 结合硬件资源优化复数矩阵向量乘
本节结合BWDSP1042处理器的硬件结构以及寻址方式,使用按列分块和模八寻址两种优化方法对复数矩阵向量乘进行优化。
3.1.1传统复数矩阵向量乘方法
传统的复数矩阵向量乘在BWDSP1042中四个执行宏中读取的方法如图3所示。
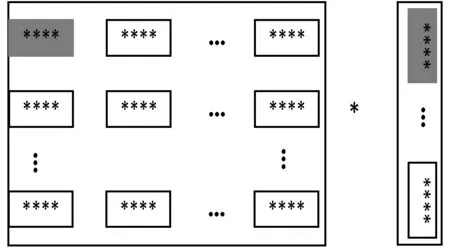
图3 传统复数矩阵向量乘在四个宏中的运算
此方法在BWDSP1042上实现的具体过程分为五步:
第一步:读取数据。取复数矩阵A中第1行相邻的四个复数,以及向量中的四个复数,其虚部和实部分别存放在四个执行宏(x、y、z、t)中。
第二步:计算并读取新的数据。矩阵A中第1行相邻的四个复数与向量中的四个复数相乘累加,其结果存放在累加器中。
第三步:重复第二步,直至矩阵中的第一行与向量计算结束。
第四步:计算y1并保存。四个执行宏的数相加得y1,将y1写入内存。
第五步:重复第一步至第四步,计算矩阵所有的行与向量乘。直至得到复数矩阵向量乘的结果。
该方法在计算过程中,y1被分为8部分,分别存储在四个执行宏中,在乘累加计算完成后,需要额外消耗资源将不同执行宏中的数相加。为解决该问题,本文提出了按列取数的方法。
3.1.2按列分块计算复数矩阵向量乘的方法
在BWDSP1042上实现复数矩阵向量乘。可采用图4中对复数矩阵按列取四个复数,分别在四个执行宏中同时与向量中的复数相乘的方法。
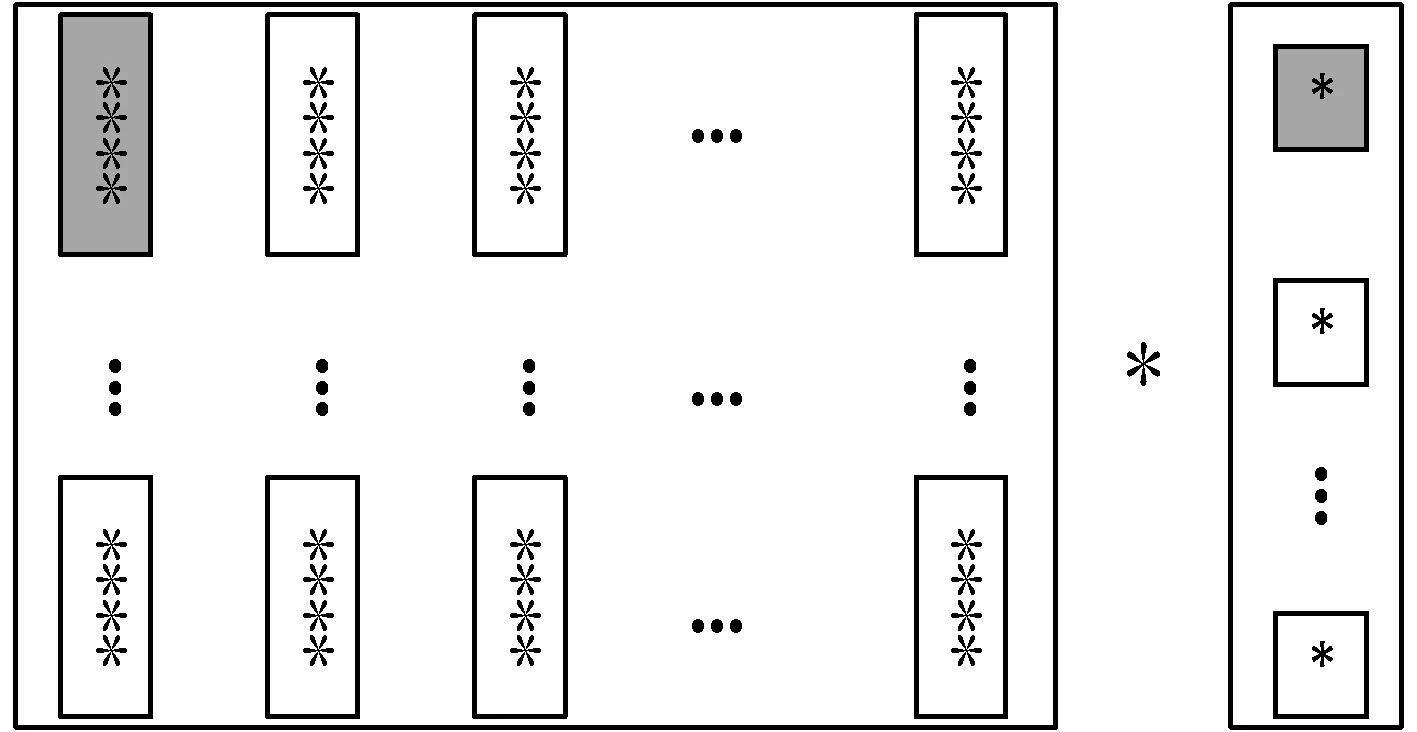
图4 按列计算复数矩阵向量乘的运算过程
此方法在BWDSP1042上具体的实现过程如下:
第一步:读取数据。读取复数矩阵中第1列的四个复数,读取向量中第一个复数,分别存在四个执行宏中。
第二步:计算并读取新的数据。第一列的四个复数分别与向量中的第一个复数相乘,并将结果存放于累加器中。同时读取矩阵下一列的四个复数,以及向量的下一个复数。
第三步:重复执行第二步,直至矩阵中前四行数据与向量乘运算结束。
第四步:保存数据。保存输出向量y1~y4的值。
第五步:重复第一步至第四步的计算方法,依次计算其他行,直至得到输出向量。
该方法循环一次,同时从四个执行宏中输出y1~y4的值,可避免不同执行宏间数据相加的执行过程,有效地节省了运行周期。
3.1.3模八寻址计算复数矩阵向量乘的方法
对于按列计算复数矩阵向量乘方法,当复数矩阵的列数是4的倍数时,读取复数矩阵会产生bank冲突。bank冲突会造成流水线停顿,在停顿的若干个cycle内依次访问冲突的地址,直到冲突解除才恢复流水。在程序中直接体现在读取数据时,每读一次数据流水线停顿两次。
为了解决bank冲突,当复数矩阵的列数是4的倍数时,采用图5的模八寻址方式,在读取数据时,执行宏x读取第一行的第一个复数,执行宏y读取第二行的第二个复数,执行宏z读取第三行的第三个复数,执行宏t读取第四行的第四个复数,再与复数向量中的数据相乘。
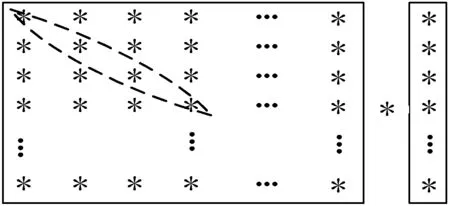
图5 模八寻址计算复数矩阵向量乘
3.2 结合软件优化技术优化复数矩阵向量乘
BWDSP1042上的软件优化技术主要包括指令并行、循环展开、软件流水三种方法[8-9]。
指令并行主要包括两个方面:一是基于SIMD指令在数据级上的并行,即同时对四个执行宏中的相同的运算单元以及通用寄存器进行相同的操作,或者同时访问数据存储器;二是在一个指令行中使用多个指令槽的技术。通过指令槽将多条语句分开,使多条指令同时执行。
循环展开是多次重复循环体代码,该方法通过使用大量代码以提高代码并行度和执行效率,本质上为向量化的思想,运用循环展开的方法将迭代间并行更改为迭代内并行,节省了大量的分支判断类指令与执行条件指令等资源,进而提高了代码效率。针对BWDSP1042的处理器,按照宏内指令编排原则,仿存及运算结果间隔两周期有效,一般规定循环展开至少三次以填补空周期行。
软件流水是通过代码的交织以实现不同循环体间的并行,运用展开来大量减少循环次数,其中单个循环体仍然顺序执行,充分运用了底层资源,进而将代码效率最大化。
使用指令并行、循环展开、软件流水优化方法在循环体内存在执行无效指令问题,针对复数矩阵向量乘运算,这些无效指令的执行严重影响了运行效率。因此,本文提出减少二级循环内的循环次数的方法,在循环体外执行循环体内未完成的部分,同时对下一次所需要的数据做处理。
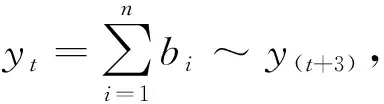
图6中指令行1读入复数矩阵中四个复数以及复数向量中的一个复数,其相应mul1、add1、acc1的运算过程在指令行4、指令行7、指令行10中执行。指令行2和指令行3中的rea2和rea3用来填充rea1的两个气泡行,其相应的乘、加、累加操作分别在mul2、mul3、add2、add3、acc2、acc3中执行,第一次执行acc3后,跳转至指令行10,继续执行。
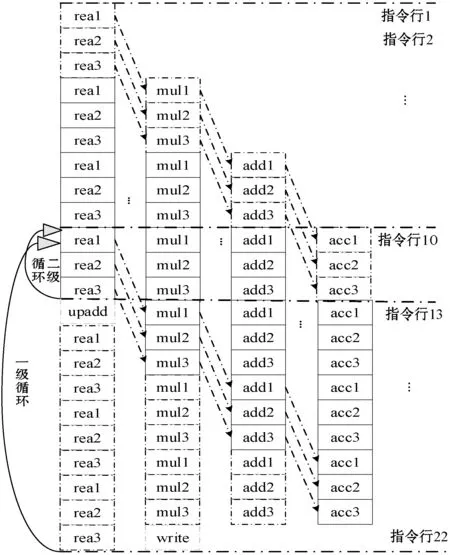
图6 二级循环次数大于9的实现方法
使用减少二级循环内的循环次数的方法时,在二级循环中执行n-9次时,跳出二级循环,此时剩余的9次循环已在二级循环体内完成了部分操作(图中指令行4至指令行12中的实线中的指令)。顺序执行指令行13至指令行21,处理该过程未完成的部分(图中指令行13至指令行21中的实线中的指令),同时在指令行13修订下次的读数地址,在指令行14至指令行24执行修正地址后的rea、mul、add操作(图中指令行14至指令行22中的虚线中的指令)。此方法通过减少二级循环的循环次数,减少了无效指令的执行次数,提高了指令利用率,从而有效缩短了运行周期。
4 测试结果与分析
本文结合硬件资源和软件优化技术提出复数矩阵向量乘优化的两种方法。方法一:按列分块与减少二级循环内循环次数相结合的方法(适用于:矩阵列非4的倍数)。方法二:模八寻址和减少二级循环内循环次数相结合的方法(适用于:矩阵列为4的倍数)。
为了验证这两种方法可有效提高BWDSP1042的数据处理速度。本实验使用BWDSP1042配套的软件开发环境ECS,分别测试了不同大小的复数矩阵向量乘。
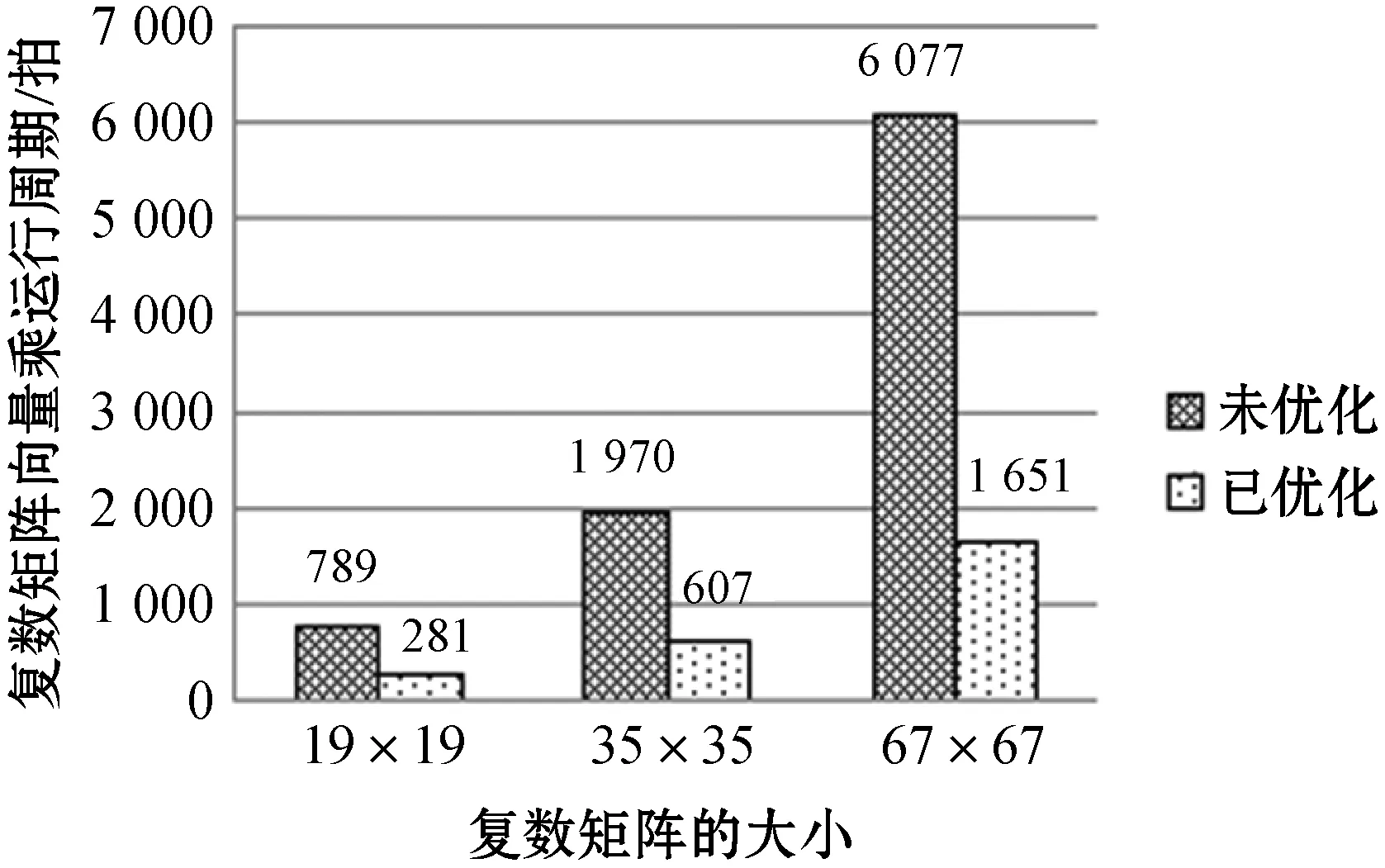
图7 按列取数方式以及减少二级循环内次数优化前后对比
图7中分别测试了复数矩阵大小为19×19、35×35、67×67时与复数向量相乘的运行周期,图中灰色柱状图表示传统按行取数在使用软件优化技术下的运行周期,白色柱状图表示在方法一下的运行周期。针对m×n的矩阵,该方法相对传统方法可减少m×13拍的四个执行宏相加的过程,另外减少了二级循环中指令行的执行次数以及零开销循环的执行次数。由图7可知:与传统算法相比,本方法使运行周期缩短了64.4%~72.8%。
图8测试了复数矩阵大小为16×16、32×32、64×64时与复数向量相乘的运行周期,三个矩阵的列数都是4的倍数,采用传统取数方式会产生bank冲突,导致每次读数流水线停顿两拍。对于m×n的矩阵,运行周期会多出拍。采用模八寻址的方式,可避免bank冲突。图8中黑色柱状图表示传统按行取数在使用软件优化技术下的运行周期,白色柱状图表示在方法二下的运行周期。由图8可知,与传统算法相比,本方法可将运行周期缩短68.4%~84.9%。
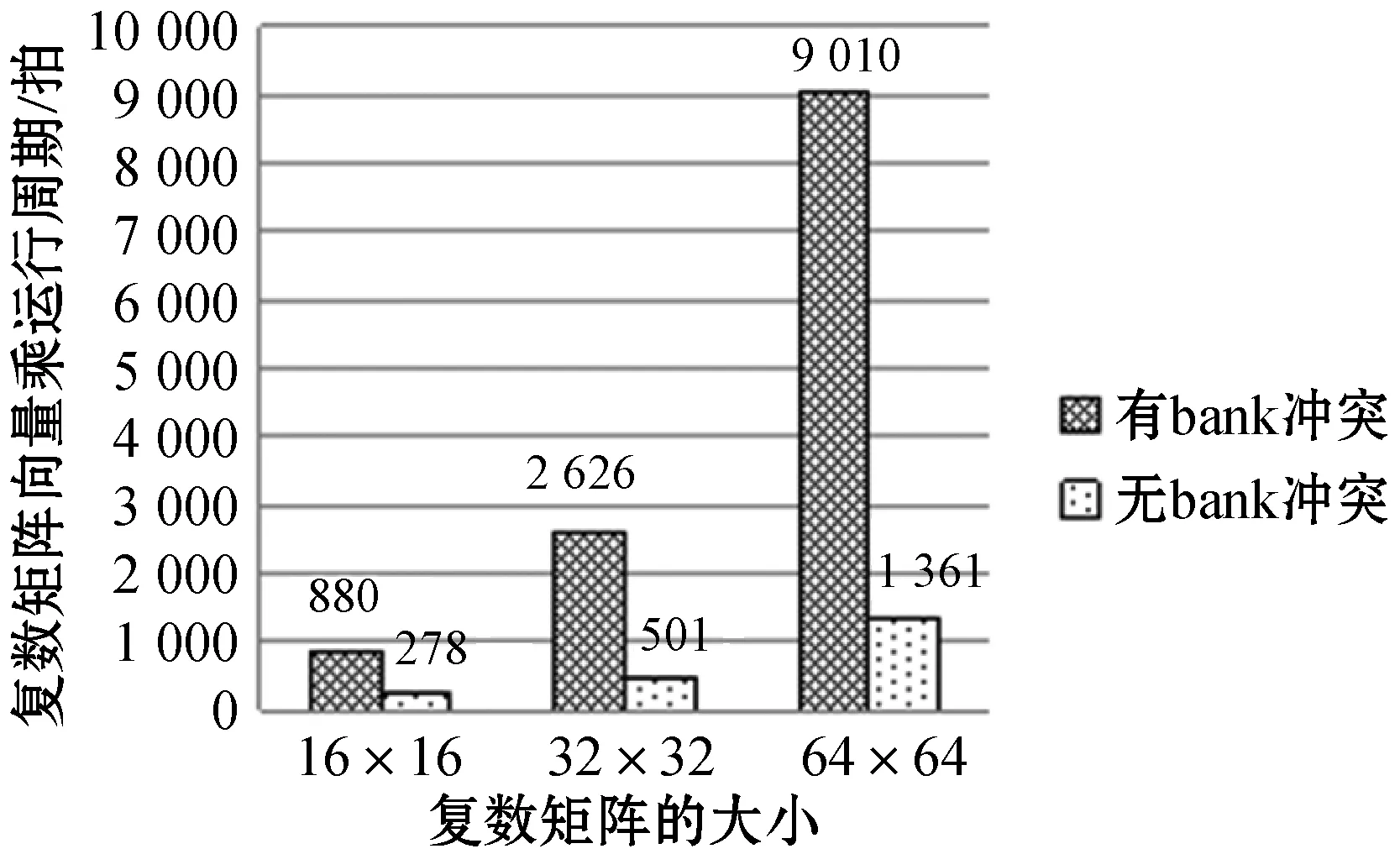
图8 采用模八寻址以及减少二级循环内次数优化前后对比
5 结 语
本文在使用指令并行,循环展开,软件流水的基础上,结合BWDSP1042的硬件结构,对复数矩阵向量乘进行优化和实现。
1) 复数矩阵采用按列取数,减少了执行宏间数据相加的过程,可降低程序的复杂度。在一定程度上缩短了运行周期。
2) 采用减少复数矩阵向量乘中的二级循环内循环次数,可以减少无效指令的执行,充分利用了BWDSP1042的计算资源和存储资源,提高了指令的运行效率。
3) 采用模八寻址的方式,消除了特殊矩阵下存在的bank冲突问题,加快了指令执行速度。
