基于异形曲面拟合引导的深度信息修复算法

王 盛 王魏平 张 真

(长春理工大学 吉林 长春 130022)

0 引 言

异形投影曲面显示系统给人们带来了更佳的临场沉浸感和增强现实感,而且异形投影曲面的空间显示特性也极大地激发了视觉感受,其被广泛应用于虚拟现实、艺术表演、文化展示、科技普及、创新创意等众多领域。伴随着投影显示系统视觉表现力的提升,异形投影曲面显示系统对深度信息的还原度依赖变得较为严苛,深度信息的获取质量将直接影响到投影显示画面的呈现效果。如果将采集得到的原始深度信息直接应用于异形投影曲面显示系统,则势必会影响到后续几何校正阶段的可靠性。

借助于RGB-D深度相机可以实时地采集投影曲面的深度信息,但由于受到RGB-D深度相机自身缺陷、采集环境、采集距离、被测曲面固有属性等因素影响,使得其采集得到的深度信息会出现表面区域丢失、深度值抖动、空间分辨率不足等重要问题。众多研究学者已经针对空洞填充及深度优化等方面开展了大量工作,各种研究成果某种程度地提高了深度信息的可用性[1]。在基于滤波理论的深度信息修补算法中,主要利用待修补区域周围的邻域深度信息或结合彩色图像来估计相关深度值[2-3]。当此类深度信息修补算法被使用时,如果待修补区域周围的深度信息相似度较高,则会出现深度信息的过修补现象;如果待修补区域处于RGB-D深度相机采集的边缘部分,则无法保证修补后深度信息的准确性。

Tomasi等[4]提出了基于非线性双边滤波的深度信息修补算法,结合使用空域信息和灰度相似性,实现了深度信息的平滑修补和保边降噪。Petschnigg等[5]提出了基于联合双边滤波的深度信息修补算法,借助彩色图像引导深度信息的修补,某种程度上解决了深度信息修补过程中出现边缘模糊的问题。Jung等[6]提出了基于联合三边滤波的深度信息修补算法,以深度信息与彩色图像的区域相似度为切入点,实现了深度信息的修补和彩色图像的增强。Esfahani等[7]充分考虑了待修补区域深度信息与像素信息之间的关系,结合双边滤波有效地实现了较小区域深度信息的修补处理。Deng等[8]结合使用像素滤波和中值滤波进行深度信息修补,达到了平滑深度信息和保边降噪的目的。

异形投影曲面深度信息的三维形态直接影响着异形投影曲面显示系统的画面呈现效果,虽然多数深度信息修复算法都能做到对空洞填补、曲面平滑、深度插值等处理,但深度信息的修复结果往往会存在过修复、失真等问题[9-10]。由于深度信息的缺失和抖动将严重影响几何形变的校正处理结果,而导致异形投影显示画面无法满足人们的正常视觉观感,因此对深度信息的修复可用性将对异形投影显示画面校正至关重要。图1所示为基于异形曲面拟合引导的深度信息修复算法系统构成图。

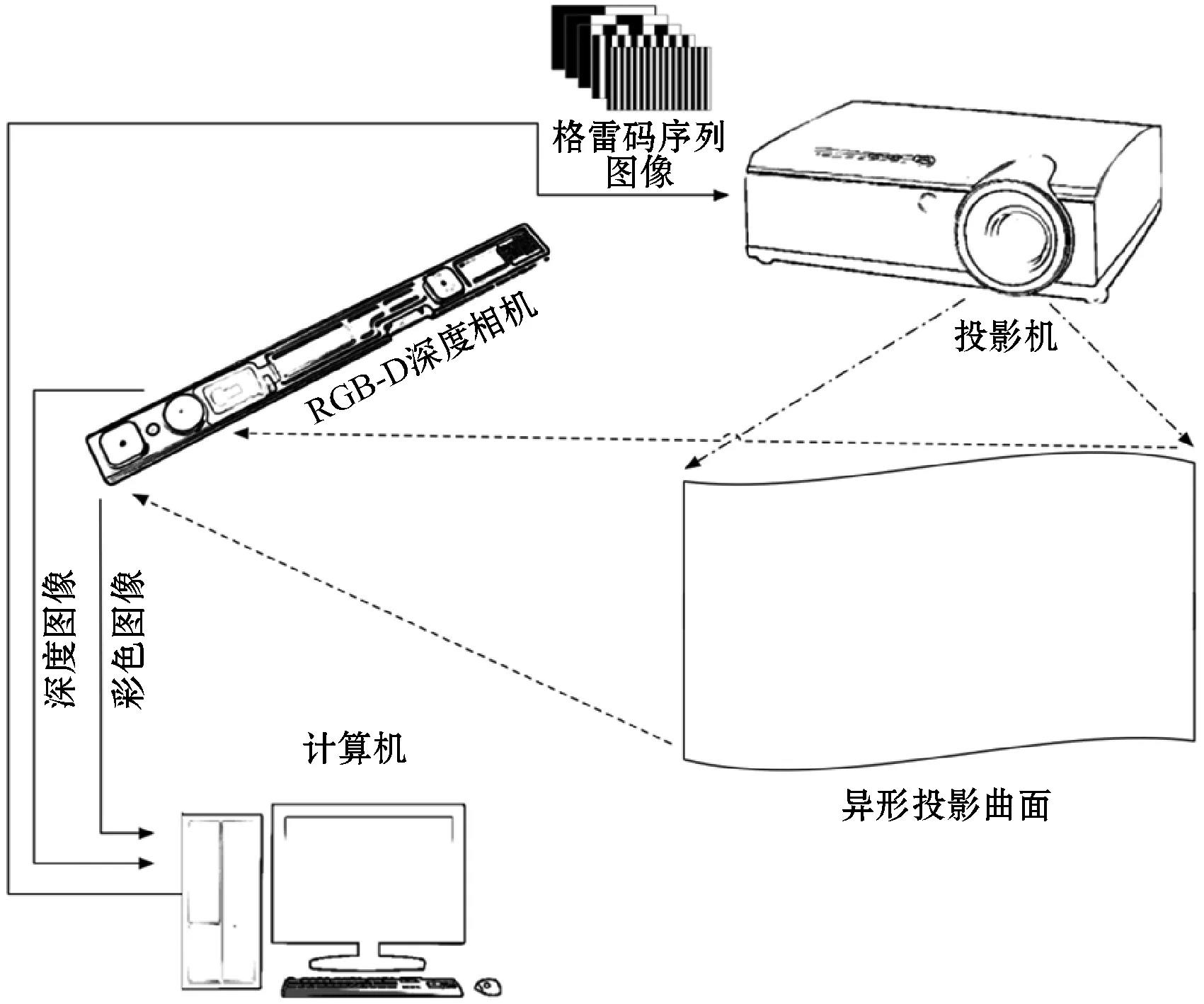
图1 基于异形曲面拟合引导的深度信息修复 算法系统构成图

基于异形曲面拟合引导的深度信息修复算法系统主要由计算机、RGB-D深度相机、投影机、异形投影曲面构成,其中:异形投影曲面用于接收投影机投射的格雷码序列图像;投影机用于投射格雷码序列图像;RGB-D深度相机用于采集异形投影曲面RGB-D空间的深度信息、异形投影曲面接收的格雷码序列图像;计算机用于获取RGB-D深度相机采集的数据信息、传输格雷码序列图像给投影机。本文深度信息修复算法将被分解为两个解算处理过程,即:异形曲面引导形态估计和曲面拟合引导深度信息修复。

1 异形曲面形态估计

为了更加合理地对异形曲面进行深度信息修复,本节将借助格雷码序列图像来体现异形曲面的形态变化情况。如果仅使用原始深度信息进行异形曲面的空间形态修复,则只能利用待修复区域周围的已知深度信息对其进行处理,而且原始深度信息自身存在的不稳定性也会直接影响深度信息修复的优化结果。由于多数情况的异形投影曲面并不存在彩色纹理,因此无法利用彩色纹理图像对深度信息的修复进行引导辅助。而本文将格雷码序列图像投射于异形投影曲面,这样不仅有利于为深度信息修复过程提供拟合引导参照,还有利于根据条纹图像的辅助作用确定有效投影区域范围。首先,根据格雷码编码原理、所需条纹数量来确定格雷码编码图像序列;然后,将格雷码编码图像序列投射于异形投影曲面,利用相机采集受异形投影表面调制的格雷码编码形变图像序列;再对编码条纹中心线进行提取识别,并得到每个编码条纹中心线的格雷码码值;最后,利用最小二乘曲线拟合方法对编码条纹形成的边界离散点进行划分,从而达到进行异形曲面形态估计的目的。

1.1 异形曲面形态纹理图像序列

由于任意两个相邻的格雷码编码值仅有1位二进制数不同,因此它具有错误最小化的编码特性。图2所示为格雷码序列的像素化示意。异形投影曲面的接收表面往往缺少形态特征而无法为深度信息修复提供参考,故需要利用格雷码编码图像序列对异形投影曲面进行三维形态的主动纹理映射。

图2 格雷码序列的像素化示意

根据格雷码编码序列的二进制数排列形式可知,格雷码编码图像序列所包含的编码图像数量将由投影分辨率、编码条纹宽度共同决定。如果投影分辨率保持不变,编码条纹宽度越大则所需编码图像数量越少,编码条纹宽度越小则所需编码图像数量越多,也就是说,投影分辨率不变的前提下,编码条纹宽度与编码图像数量成反比。

根据式(1)即可计算得到格雷码编码图像序列所含图像数目为:

式中:n表示格雷码编码图像序列所包含的编码图像数量;Sp表示投影机投射分辨率;Sn表示编码条纹所占像素宽度值。

根据格雷码编码序列的二进制数排列形式,生成t幅格雷码编码图像序列GCPs={GCPs1,GCPs2,…,GCPst}。通过投影机依次将格雷码编码图像序列GCPs的每幅编码图像投射于异形曲面,同时使用RGB-D深度相机单元依次采集投射于异形投影曲面的每幅编码图像,得到RGB-D深度相机采集的t幅格雷码编码图像序列CGCPs={CGCPs1,CGCPs2,…,CGCPst}、RGB-D深度相机采集的t组深度信息值序列DGCPs={DGCPs1,DGCPs2,…,DGCPst},编码图像序列CGCPs与深度信息值序列DGCPs具有对齐关系,且深度信息值序列DGCPs对齐于编码图像序列CGCPs。

1.2 序列编码条纹提取识别

通过相机采集得到格雷码编码形变图像序列后,需对编码条纹进行提取及解码以获取各编码条纹的格雷码值。为了准确地对序列编码条纹进行中心线提取与识别,需利用色彩空间转换将格雷码编码图像序列CGCPs={CGCPs1,CGCPs2,…,CGCPst}输出为YUV色彩空间的Y通道编码图像序列YGCPs={YGCPs1,YGCPs2,…,YGCPst},其具体色彩空间的转换过程可通过式(2)实现。正因亮度信息分量Y更好地表达了各像素点的亮度等级信息,所以对序列编码条纹中心线的提取过程将使用亮度信息分量Y进行。

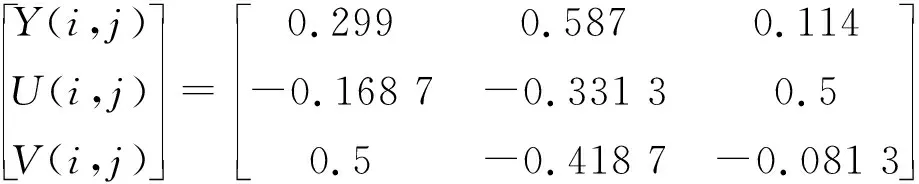
式中:Y(i,j)、U(i,j)、V(i,j)、R(i,j)、G(i,j)、B(i,j)分别表示某图像中第i行第j列像素点的Y、U、V、R、G、B通道信息分量值。

由于序列编码条纹中心线位于波形曲线的波峰和波谷处,因此需要使用线性平滑滤波器对Y通道编码图像序列YGCPs进行平滑处理,使对序列编码条纹中心线的提取结果更加准确[11-12]。另外需要注意:对横向序列编码条纹进行平滑处理时,需使用纵向线性平滑滤波器;对纵向序列编码条纹进行平滑处理时,需使用横向线性平滑滤波器。

格雷码编码图像序列所包含编码条纹的码值是由二进制值决定的,因此提取出序列编码条纹中心线后还要对Y通道编码图像序列YGCPs进行二值化处理,再利用二值化图像即可对各个序列编码条纹进行解码识别。本文算法的序列编码条纹由横条纹和纵条纹构成,根据格雷码解码原理对Y通道编码图像序列YGCPs进行解码处理后,即可得到所有序列编码条纹中心线各像素点的格雷码值,并且每个中心线像素点均具有横向和纵向两个格雷码值。根据解码码值与编码码值之间的关系,得到各中心线像素点之间的对应归属关系,从而为离散点曲线拟合过程提供基础。

1.3 编码条纹分段离散点曲线拟合

一般情况而言,网格曲面区域的平缓程度可通过其区域边界曲线反映出来,即:异形曲面区域较平缓则其边界曲线曲率较小、异形曲面区域起伏较大则其边界曲线曲率较大。上述序列编码条纹的提取识别过程相当于将异形曲面进行了网格划分,由于异形曲面形态起伏未知且复杂多样,为了能够更好地表达异形曲面各网格区域形态变化趋势,并为后续异形平缓曲面区域的合并划分提供基础,则预先对各异形曲面网格区域的边界曲线进行离散点拟合[13-14]。

最小二乘法曲线拟合能够使样本回归计算值与已知样本数据值的总体误差最小,而多项式函数曲线拟合形式也更加符合边界曲线的函数表达,因此将使用多项式函数结合最小二乘法对边界曲线进行拟合估计,该多项式函数可由式(3)表示。

y=lnxn+ln-1+…+l1x+l0

(3)

式中:ln表示多项式函数的第n个参数值。

因为异形曲面区域的边界曲线应具有最简曲线函数形式,为了确保多项式函数曲线拟合结果符合于曲面边界曲线,并且能够有效地降低曲线拟合算法复杂性和减少拟合过程累积误差,对边界曲线的拟合估计过程将使用二次多项式函数。利用离散点曲线拟合方式,即可得到所有异形曲面区域的边界曲线方程。

2 曲面拟合引导深度信息修复

为了实现对异形投影曲面的深度信息修复,则需要合理地利用已采集到的原始深度信息和曲面形态特征,并使用异形投影曲面形态特征为原始深度信息的修复过程提供参照。利用三维曲面数理模型准确拟合出平缓曲面区域的异形曲面方程,再根据各异形曲面方程分别对其内部的所有坐标点进行深度信息重计算,进而实现利用曲面拟合引导的异形曲面深度信息修复处理[15]。

2.1 异形平缓曲面区域划分

虽然序列编码条纹已将异形投影曲面进行了网格划分,但这些被网格划分的单元曲面区域并不能很好地表达异形曲面形态变化趋势[16],也就是说,局部曲面区域形态并不能合理地表示整体曲面形态变化趋势,因此更为准确的计算过程便是:将具有相似边界曲线方程的单元曲面区域划归为同一异形平缓曲面区域。

通过对各单元曲面区域边界曲线的离散点曲线拟合,可以估计得到每个单元曲面区域的四个外部边界曲线方程,上边界曲线方程、下边界曲线方程、左边界曲线方程、右边界曲线方程可分别表示为BCU、BCD、BCL、BCR。由于使用每个单元曲面区域的外围边界曲线方程作为平缓曲面区域划分依据,因此各边界曲线方程计算值的相似度对异形平缓曲面区域划分极为关键。

两个二次多项式边界曲线方程的相似度可利用SPD距离进行评判,由式(4)可表示SPD距离的计算过程,其中:SPD(A,B)表示曲线方程A与曲线方程B的对应点对距离之和;ai表示曲线方程A的第i个坐标值、bi表示曲线方程B的第i个坐标值;d(ai,bi)表示坐标值ai与坐标值bi之间的欧氏距离。

假设存在SF1、SF2两个单元曲面区域,如果在指定取值区间内SF1与SF2的各个边界曲线方程都对应具备相似性,则可以认定二者属于同一个异形平缓曲面区域,否则二者分属不同异形平缓曲面区域。通过对整体异形投影曲面进行平缓曲面区域划分,将使得各异形平缓曲面区域的曲面拟合方程更为有效和合理。

2.2 平缓区域离散点曲面拟合及深度信息修复

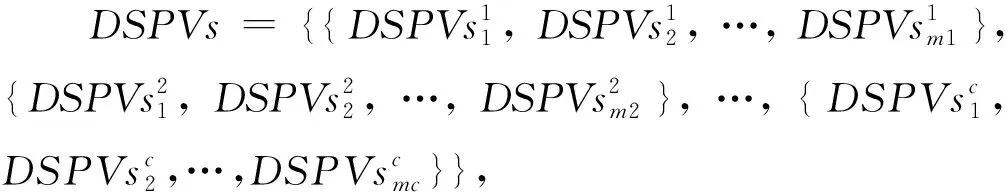
由于异形平缓曲面区域寻求的曲面过渡态势要尽可能避免复杂形变,因此曲面拟合方程形式为最基本的二次曲面方程表达。当对每个异形平缓曲面区域进行二次方程拟合时,根据二次曲面拟合表达式(5)并利用最小二乘拟合法,估计得到与每个异形平缓曲面区域相对应的二次曲面方程拟合参数序列SFPVs,且SFPVs={{S01,S11,S21,S31,S41,S51},{S02,S12,S22,S32,S42,S52},{S0c-1,S1c-1,S2c-1,S3c-1,S4c-1,S5c-1},{S0c,S1c,S2c,S3c,S4c,S5c}},其中:{S0c,S1c,S2c,S3c,S4c,S5c}表示第c个异形平缓曲面区域的拟合参数值。

z=S0x2+S1y2+S3xy+S3x+S4y+S5

(5)

式中:x、y、z分别表示异形平缓曲面区域中各像素点对应的三维空间X轴坐标值、Y轴坐标值、Z轴坐标值。经过对原始异形平缓曲面区域进行离散点曲面拟合处理后,极可能会出现拟合曲面与三维空间离散点存在较大误差等情况,此时则需要再次对出现异常拟合的异形平缓曲面区域进行重划分[17]。对异形平缓曲面区域进行重划分采用的规则为:如果某个单元曲面区域内各离散点Z轴坐标值与其所属平缓区域曲面拟合计算得到的对应Z轴坐标值之间所有离散点的误差之和均值大于设定的最大容差值,则将该单元曲面区域从其所属平缓区域剔除,并再次对重划分的平缓区域进行曲面拟合;而对于被剔除的单元曲面区域来说,将它与其周围八个相邻的单元曲面区域组合,再使用离散点曲面拟合方式得到该单元曲面区域的二次曲面方程。通过使用异形平缓曲面区域重划分规则对全部曲面区域进行优化处理,直到每个被区域划分的异形平缓区域离散点曲面拟合误差均能达到合理范围之内,进而拟合得到最优的二次曲面方程参数序列SWPVs,且SWPVs={{WS01,WS11,WS21,WS31,WS41,WS51},{WS02,WS12,WS22,WS32,WS42,WS52},…,{WS0c,WS1c,WS2c,WS3c,WS4c,WS5c}。

利用已拟合得到的二次曲面方程参数序列SWPVs和二次曲面拟合表达式,即可根据每个异形平缓曲面区域内所有像素点的三维空间x、y坐标值,计算得到各像素点对应的三维空间z坐标拟合优化值,从而实现对异形投影曲面的深度信息优化修复。

3 深度信息修复算法验证

本文算法将格雷码编码图像序列投射于异形曲面,通过主动引导的方式实现异形投影曲面的形态检测、平缓曲面区域划分、平缓曲面区域拟合以及区域深度信息修复等操作,从而达到异形曲面拟合引导的深度信息修复目的。

为了检验本文所提算法的可行性及有效性,在编码序列图像和深度信息采集阶段,使用C++编程语言和RGB-D传感器(Kinect v2.0)实现初始数据的采集存储操作;在编码条纹提取识别、分段离散点曲线拟合、平缓曲面区域划分、区域离散点曲面拟合等处理阶段,采用Python编程语言并结合Plotly、Numpy等类库支持实现修复算法处理过程的具体操作。由于本文算法强调了异形曲面拟合对深度信息修复的引导性作用,故将以具有普适性的随机异形投影曲面为算法验证环境,而不是使用特殊布置的规则性投影表面为算法验证环境。

分别将横纵两组格雷码编码图像序列投射于异形投影曲面,从而使得异形曲面具有被动纹理特征,以达到对异形投影曲面进行几何形态感知的目的。图3所示为投射了横向格雷码编码图像的异形投影曲面。图4所示为投射了纵向格雷码编码图像的异形投影曲面。

图3 投射横向格雷码图像的异形投影曲面

然后使用RGB-D深度相机中彩色图像传感器采集到的横纵格雷码序列图像,并根据格雷码解码原理即可得到所有序列编码条纹对应像素点的格雷码码值,再结合序列编码条纹对整体异形投影曲面的网格化分割关系,便可以得到每个单元曲面区域中四个边界曲线的平面离散点坐标值。

在已知边界曲线离散点集的确切归属前提下,即可利用多项式函数表达式(3)对各个边界曲线离散点集进行多项式曲线函数拟合,从而得到每个单元曲面区域中四个边界曲线的多项式函数描述,以确定各单元曲面区域的异形平缓曲面区域划分归属目的。图5所示为多项式边界曲线函数拟合样例。式(6)为图5中多项式边界曲线函数拟合方程。

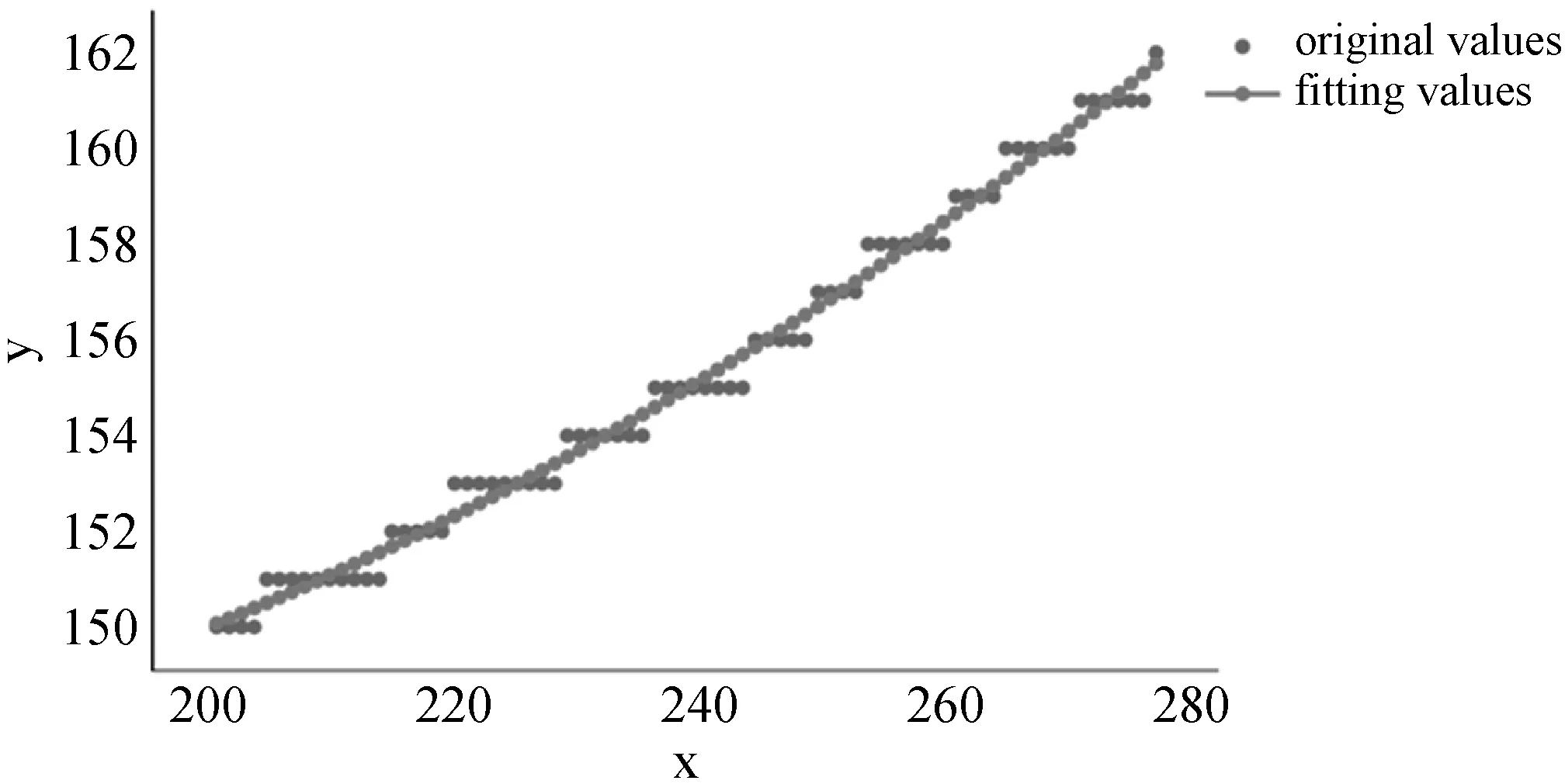
图5 多项式边界曲线函数拟合样例

y=0.000 671 4×x2-0.164 3×x2+156

(6)

利用所有单元曲面区域的多项式边界曲线拟合方程结果,再根据边界曲线的SPD相似度计算匹配关系,即可得到每个异形平缓曲面区域的划分归类及其包含的像素点集合。接着利用RGB-D深度相机中深度信息传感器对各异形平缓曲面区域的所有像素点进行三维空间映射,便可以得到每个平缓曲面区域中各离散像素点的三维空间坐标值。

再结合使用二次曲面拟合表达式(5)对平缓曲面区域的离散空间点集进行最小二乘估计,计算得到每个异形平缓曲面区域的二次曲面方程,而后将离散空间点的X轴坐标值、Y轴坐标值传入它对应的二次曲面方程,即可计算得到异形曲面拟合引导的深度信息修复值。图6所示为异形平缓曲面区域的二次曲面拟合修复样例1。式(7)为图6中平缓曲面区域的二次曲面拟合方程。

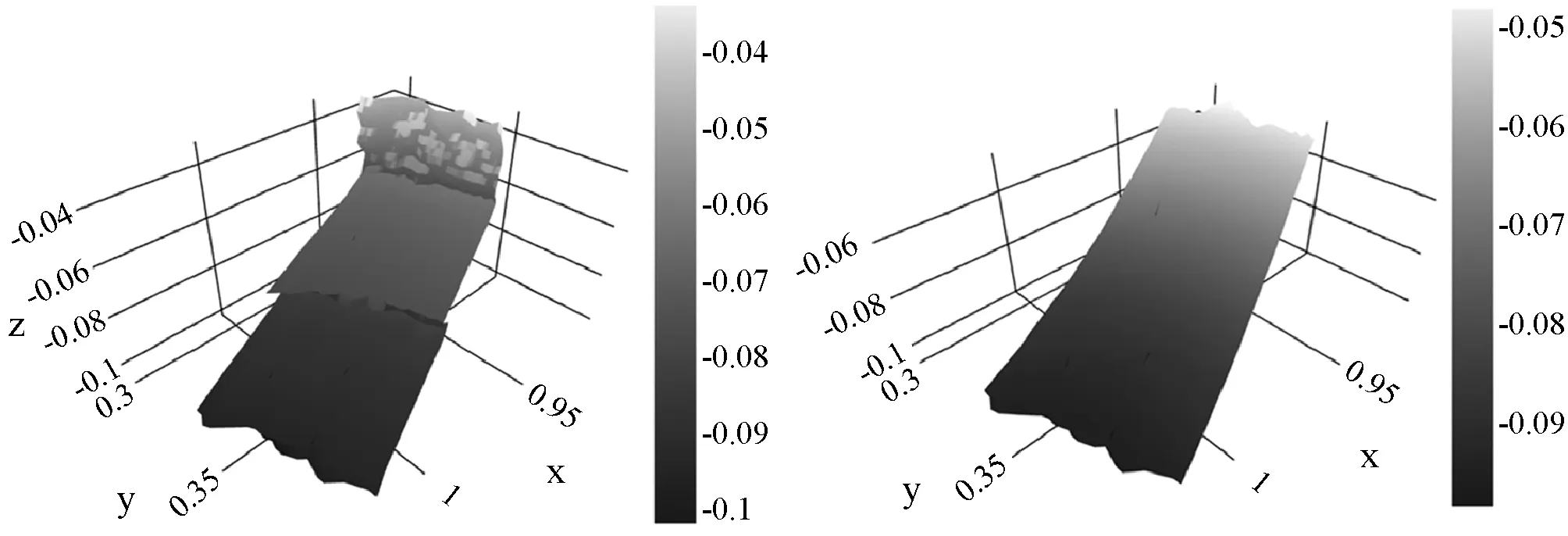
(a) 原始样例 (b) 修复后样例图6 异形平缓曲面区域的二次曲面拟合修复样例1

z=.48×x2-0.81×xy+2.66×y2-

4.94×x-1.14×y+2.71

(7)

图7所示为异形平缓曲面区域的二次曲面拟合修复样例2。图8所示为异形平缓曲面区域的二次曲面拟合修复样例3。

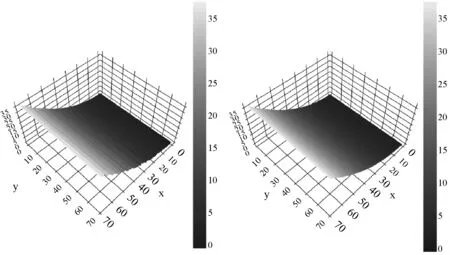
(a) 原始样例 (b) 修复后样例图7 异形平缓曲面区域的二次曲面拟合修复样例2

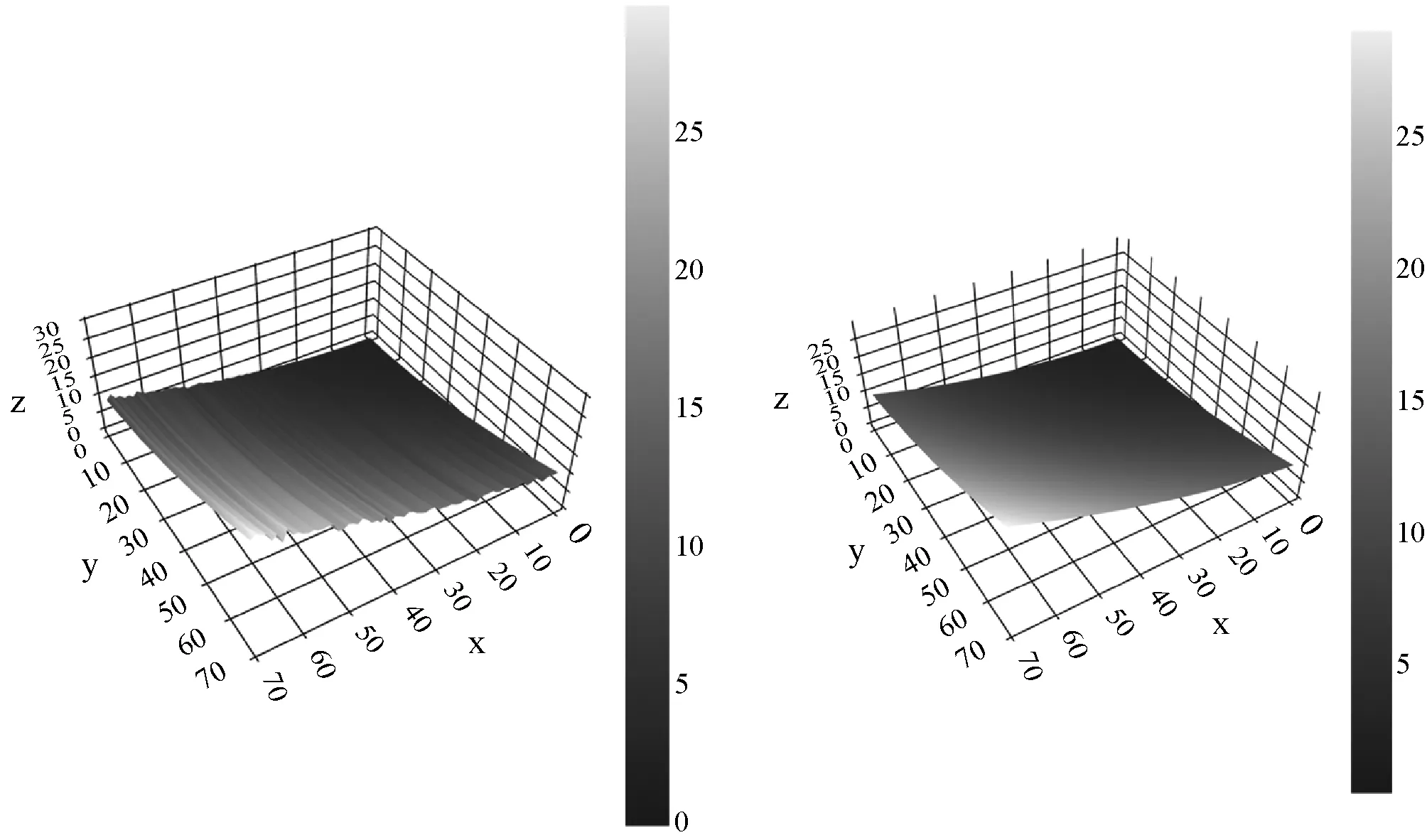
(a) 原始样例 (b) 修复后样例图8 异形平缓曲面区域的二次曲面拟合修复样例3

图9-图10所示为本文算法与双边滤波算法修复结果的样例对比。经过对修复后深度值与基准深度值之间的差异进行定量分析得到:误差最大值约为1.463 6 cm,误差最小值约为0.06 cm,误差中值约为0.235 7 cm,误差中位值约为0.152 5 cm。从异形平缓曲面区域的二次曲面拟合修复样例结果可以看出,本文算法虽未使用过多复杂的数理计算模型,而只是使用了最基本的多项式函数、二次曲面函数进行拟合估计计算,但是却得到了非常理想的深度信息拟合修复效果。

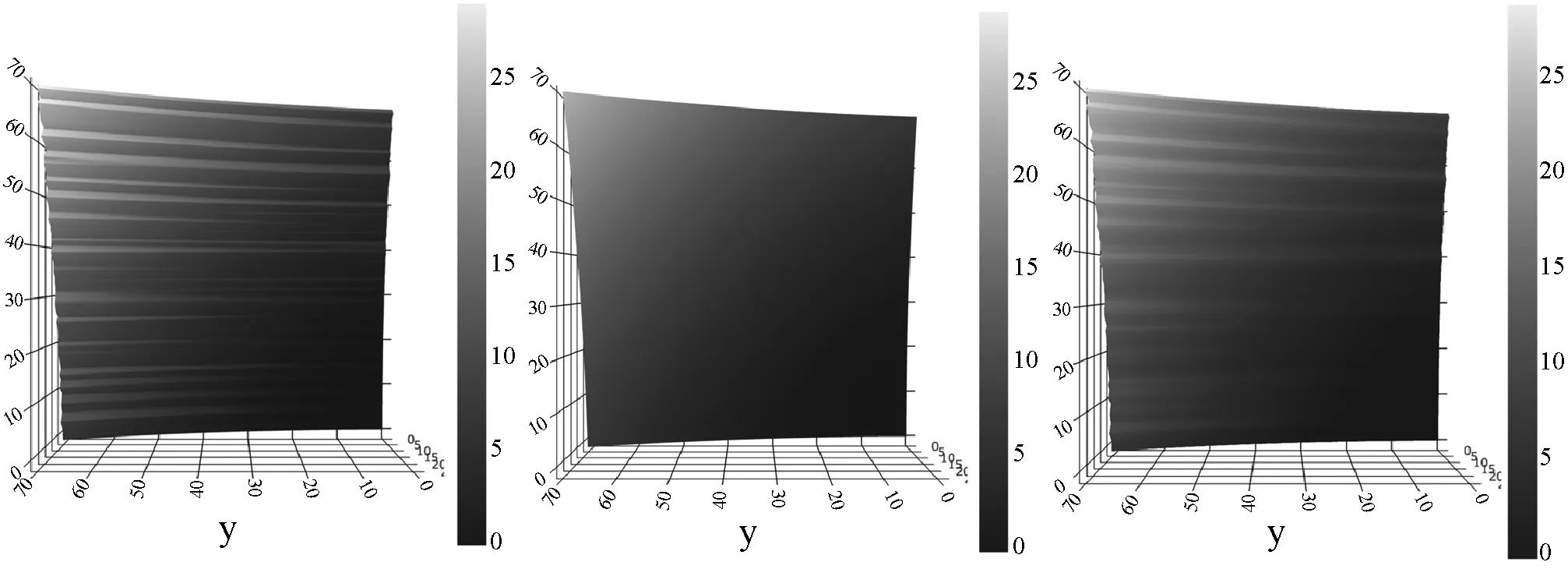
(a) 未修复样例 (b) 本文算法修复样例 (c) 双边滤波修复样例图10 算法修复对比样例2

4 结 语

本文针对异形曲面的深度信息修复问题,提出了基于异形曲面拟合引导的深度信息修复算法。在进行异形曲面深度信息修复过程中,该算法不仅可以做到异形投影曲面几何形态的变化趋势表达,还可以做到异形投影曲面的平缓曲面区域划分、异形投影曲面的三维曲面拟合等操作,从而达到异形曲面拟合引导的深度信息修复目的。本文算法通过格雷码序列图像的编码条纹形变来表达异形曲面几何变化趋势,再根据异形曲面的几何形态变化趋势对平缓曲面区域进行划分,最后利用三维曲面数理模型拟合出的曲面方程对原始深度信息进行平滑修复。本文深度信息修复算法根据异形曲面的形态拟合,能够实现对深度信息的原始值优化和缺失区域填补,提高了异形曲面深度信息的可用性、保真度、合理性等,虽然如此,但关于此领域的研究仍有提升空间。