二维变分模态分解联合快速非局部均值的医学超声图像去噪方法
2023-04-07闫洪波杨文英赵蓬勃
闫洪波 刘 霈 徐 洋 杨文英 赵蓬勃
1(内蒙古科技大学机械工程学院 内蒙古 包头 014010) 2(包头医学院第一附属医院 内蒙古 包头 014010) 3(国药北方医院(包医三附院) 内蒙古 包头 014030)
0 引 言
医学超声具有无创、低成本、实时成像等优点,被广泛地应用于临床医学诊断中。超声探头向体内发射出某一频率的超声波,由于各个器官声阻抗不同,超声波会在传播过程中在组织表面发生散射形成一系列相干波,这些相干波相互干涉形成斑点噪声[1]。斑点噪声的存在会大大影响医生对超声图像中有效信息的识别,增大诊断难度。目前,能够有效去噪的同时还能保留良好的边缘信息是超声图像去噪研究的热点和难点[2]。
变分模态分解(Variational Mode Decomposition,VMD)在2014年由Zosso等[3]提出,是一种新的非递归式的信号处理方法,有坚实的理论基础,其算法中融入了自适应维纳滤波,有效避免了模态混叠和边界效应,具有良好的噪声鲁棒性。刘长良等[4]首次将VMD算法应用到了故障诊断中来处理信号,其中分解的各模态中携带着不同频率的故障信息,方便后续精确的提取故障信息。2015年Dragomiretskiy等[5]提出二维变分模态分解(Two-dimensional variational mode decomposition)算法,该算法将处理一维信号扩展到了二维的图像上。刘嘉敏等[6]通过二维变分模态分解将图像分解为一系列不同中心频率的子模态,保留其低频部分进行自适应中值滤波处理,能够较好地保留图像边缘细节,客观评价参数较其他方法也有很大的改善。
本文在充分掌握超声图像噪声产生的原理和分布情况,提出了一种基于2D-VMD和快速非局部均值的去噪方法。将超声图像经过2D-VMD分解,该算法有较好的噪声鲁棒性[7],弥补了KNLM滤波算法没有鲁棒性的缺点,并保留低频部分进行快速非局部均值去噪处理得到去噪图像。实验结果表明,该方法能够得到比传统滤波方法更好的效果,最大程度地滤除噪声、保留边缘信息,为医生进一步诊断提供便利。
1 二维变分模态分解
2D-VMD是根据一维VMD基础上进行了扩展,将图像自适应的分解成K个不同中心频率的子模态,具有很高的非递归性和自适应性,图像经分解后仍能很好地保持其自身特性。
1.1 二维解析信号
在一维时域中,将添加的原始信号进行希尔伯特变换作为虚部,得到解析信号如下:
fAS(t)=f(t)+jH{f}(t)
(1)
一维变分模态分解中解析信号在频域中的定义为:
解析信号频谱存在单边特性,将模态的频谱转移到基带,使用混合指数将其估计在中心频率上。分界面相当于一个向量,记为wk,此二维解析信号在频域上的定义为:
根据傅里叶变换的特性,二维解析信号可以定义为:
(4)
式中:*表示卷积并且在转换保持可分,根据解析信号参考方向wk排列。
1.2 2D-VMD
2D-VMD算法实质上是一个变分问题的求解过程,将输入信号分解得到K个离散的子模态函数uk(t),使得每个模态函数的估计带宽之和最小。对应的变分模态模型为:
式中:{uk}={u1,u,…,uk}是分解后得到的K个模态函数;{wk}={w1,w2,…,wk}为各模态函数的中心频率;K为模态分解数量。
1.3 乘法算子交替方法优化2D-VMD
使用二次惩罚系数和拉格朗日乘子可以把约束性变分问题调整成为非约束性变分问题,得到拉格朗日表达式如下:
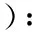
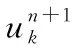
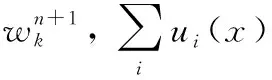
∀w∈Ωk,Ωk={w|〈w,wk〉}
(8)
同样在频域,可得:
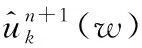
1.4 2D-VMD算法
2D-VMD算法在频域中进行更新,然后进行傅里叶逆变换,其具体过程如下:
(2) 根据式(8)、式(9)在频域内更新uk、wk;
(3) 更新λ:
2 快速非局部均值
NLM[8]算法中目标像素不但与邻域像素有相关性,而且和整幅图像的其他像素也有相关性。图像中通过与所有结构相似的像素加权取平均值得到当前的像素值,任一像素的权值可用以它为中心的像素块和当前像素块为中心的高斯加权欧氏距离求得[9]。
NLM滤波后有:
式中:f′表示含噪图像;i,j表示图像任一像素;ω为权值函数;I为像素集合。
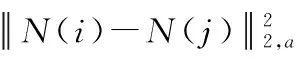
假设图像共有N个像素点,搜索窗口大小为D×D(D=2×Ds+1),邻域窗口大小d×d(d=2×ds+1),两个窗口邻域间相似度的时间为O(d2),计算每个像素点与搜索窗口内D2个像素间的相似度,因此NLM复杂度为O(ND2d2)。
在NLM算法中每次计算邻域间距离时,都得遍历两个邻域逐对像素点求差值,从而造成运算时间过长。构建关于像素差值的积分图像:
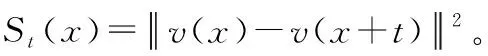
在计算邻域V(x)和V(y),y=x+t的间距离时,便能在常量时间内完成:
St(x1-ds-1,x2-ds-1)-St(x1+ds,x2-ds-1)-
St(x1-ds-1,x2+ds))
(14)
经过以上算法,复杂度降为O(ND2)。
3 D-VMD联合FNLM去噪算法
根据2D-VMD算法的原理,自适应地将图像分解成一系列中心频率不同的子模态。低频部分保留图像大部分信息,但仍含有一部分噪声。噪声主要集中在高频部分,在加入斑点噪声方差为0.2时,测得PSNR值为3.671 5,相比于低频部分PSNR值30.567 3,几乎已经不含图片信息了,所以将高频模态舍去,保留低频模态,采用快速非局部均值再次对低频部分图像进行去噪。具体流程见图1。
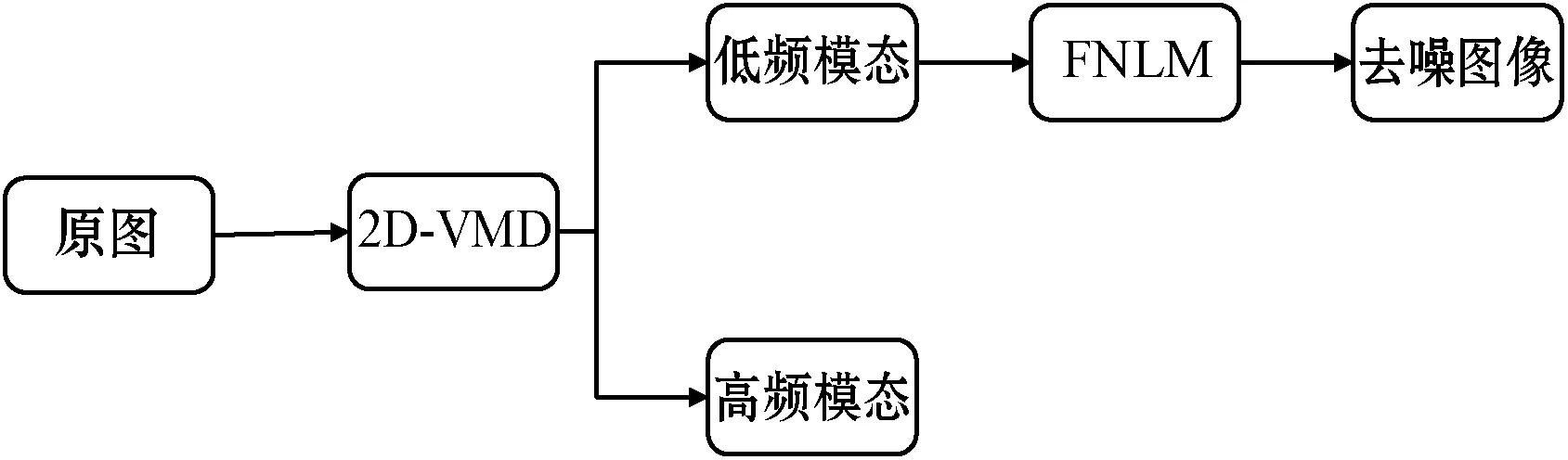
图1 本文方法流程
4 实验结果分析
实验采用图像大小为512×512的lena图片和包头医学院第一附属医院提供的超声盆腔图片进行验证,利用峰值信噪比(PSNR)和结构相似度(SSIM)作为图像质量评价标准。PSNR值体现的是去噪能力,值越大说明去噪效果越好;SSIM衡量两幅图片的相似程度,值越大说明图像越相像。为了验证2D-VMD联合FNLM算法的有效性,与经典空间滤波器如Lee[10]、Frost[11]、Kuan[12]滤波器,以及近几年提出的BM3D[13]、OBNLM[14]、FNLM滤波器进行比较。实验在MATLAB 2018a中进行测试,在图像中加入噪声方差为0.02、0.04、0.06、0.08、0.2、0.4、0.6、0.8的斑点噪声,采用以上方法和新方法进行去噪处理,通过评价参数PSNR和SSIM值对去噪效果进行对比。
使用2D-VMD算法将图像分解为K个中心频率不同的模态,经过大量调试,其参数α=25,模态数k=2,得到的效果最好。将分解后得到的低频模态经过FNLM算法处理滤波,平滑参数h=20,得到效果最好。其他滤波算法参数都调至PSNR、SSIM值最优,与提出算法进行比较。
实验分别对测试图lena图像和真实超声图像加入噪声方差为0.02~0.8的斑点噪声,用本文提出算法进行滤波。实验结果分别与其他算法进行比较。图2是噪声方差为0.2斑点噪声的lena图经过各滤波算法后得到的结果图,表1、表2为噪声方差0.02~0.8的各滤波方法去噪后的PSNR、SSIM值。在低噪声方差下,BM3D和传统NLM滤波算法都有较好的去噪效果,但BM3D滤波随着噪声方差的增大其PSNR值和SSIM值也大大降低,传统FNLM滤波算法噪去噪的同时也会牺牲一定的边缘细节,另外几种滤波算法在噪声方差为0.2时,已经很难滤除掉斑点噪声,图像细节难以辨识,严重影响对图像的分析,随着噪声方差的加大其PSNR值和SSIM值也明显降低。本文提出算法能够在有效去噪声的同时保留边缘细节,在噪声方差为0.2时其滤波效果明显优于其他算法,而且在高噪声下图像仍能得出比其他滤波方法更好的PSNR值和SSIM值。

(a) 原图 (b) 噪声图

(c) BM3D滤波 (d) OBNLM滤波

(e) Forst滤波 (f) Kuan滤波
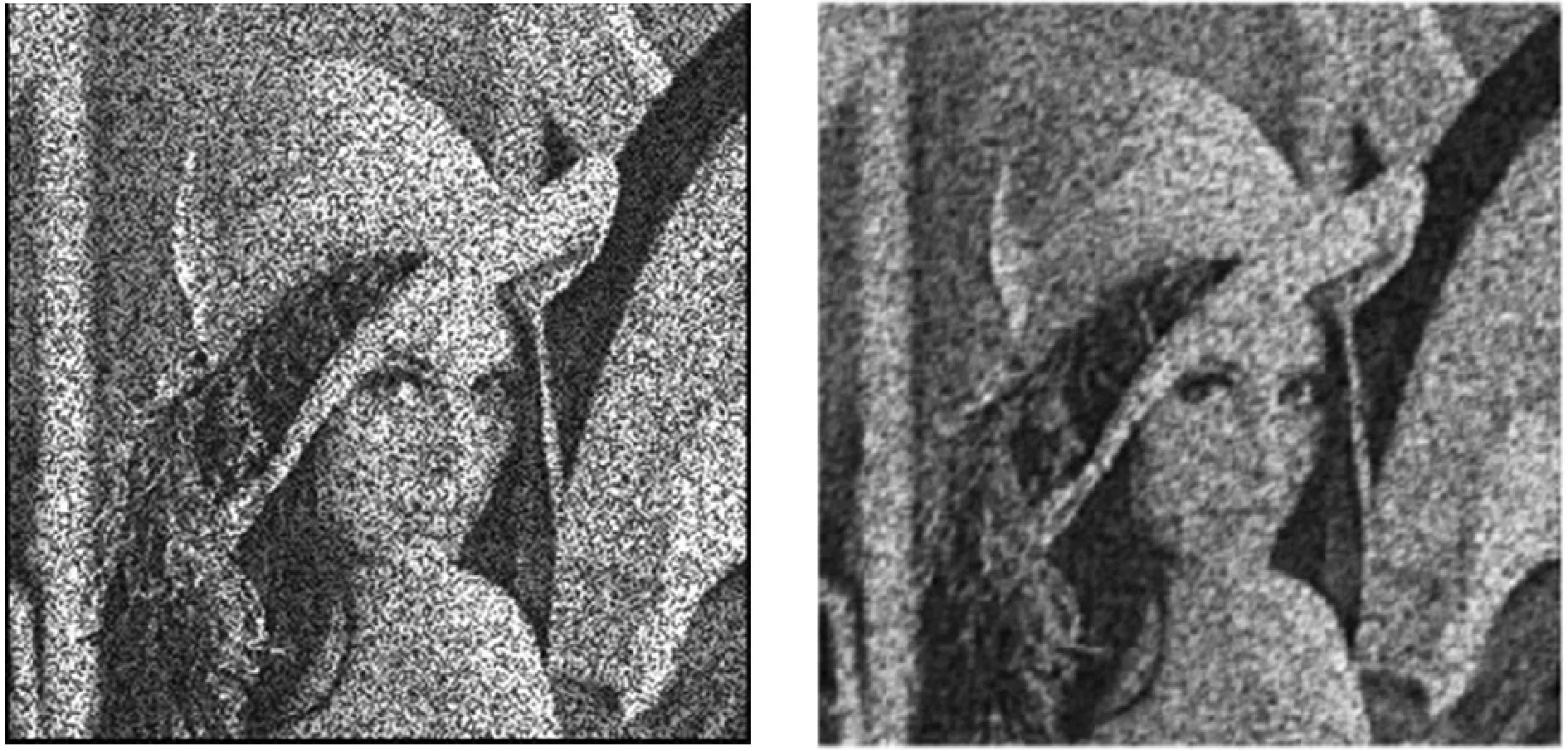
(g) Lee滤波 (h) 2D-VMD滤波

(i) FNLM滤波 (j) 本文算法滤波图2 噪声方差为0.2的lena图
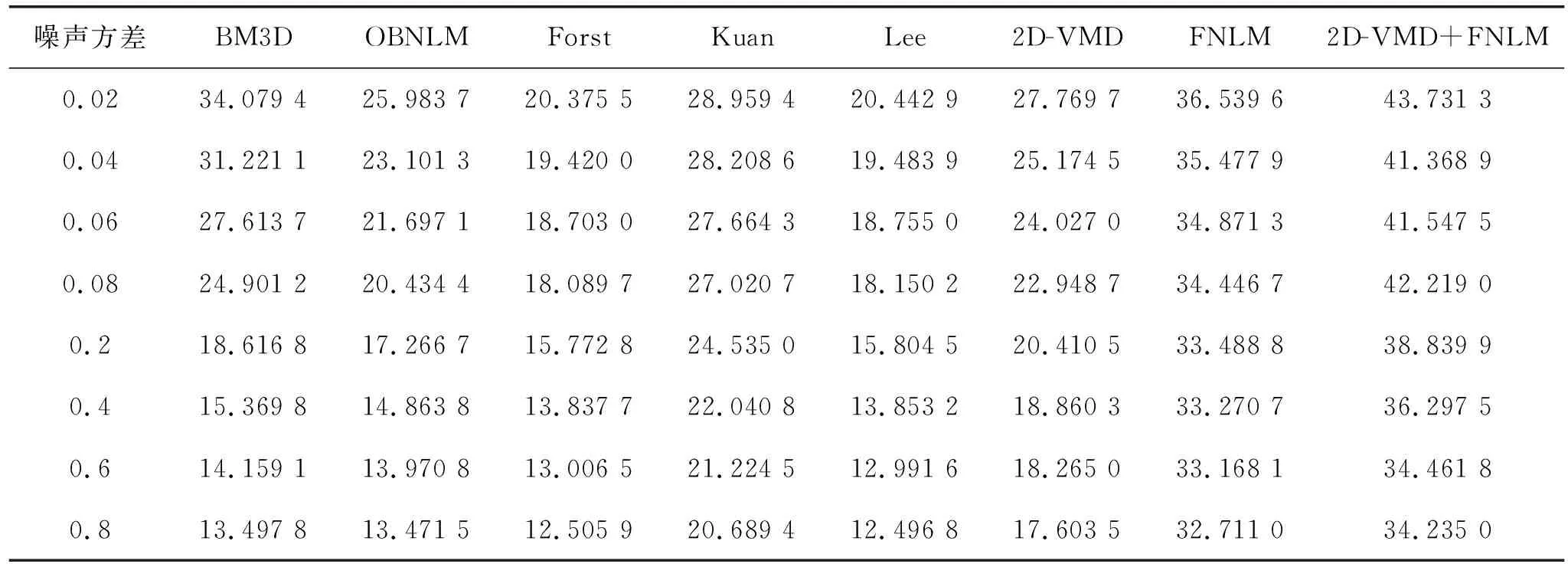
表1 lena图像在不同噪声方差下不同滤波算法的PSNR值
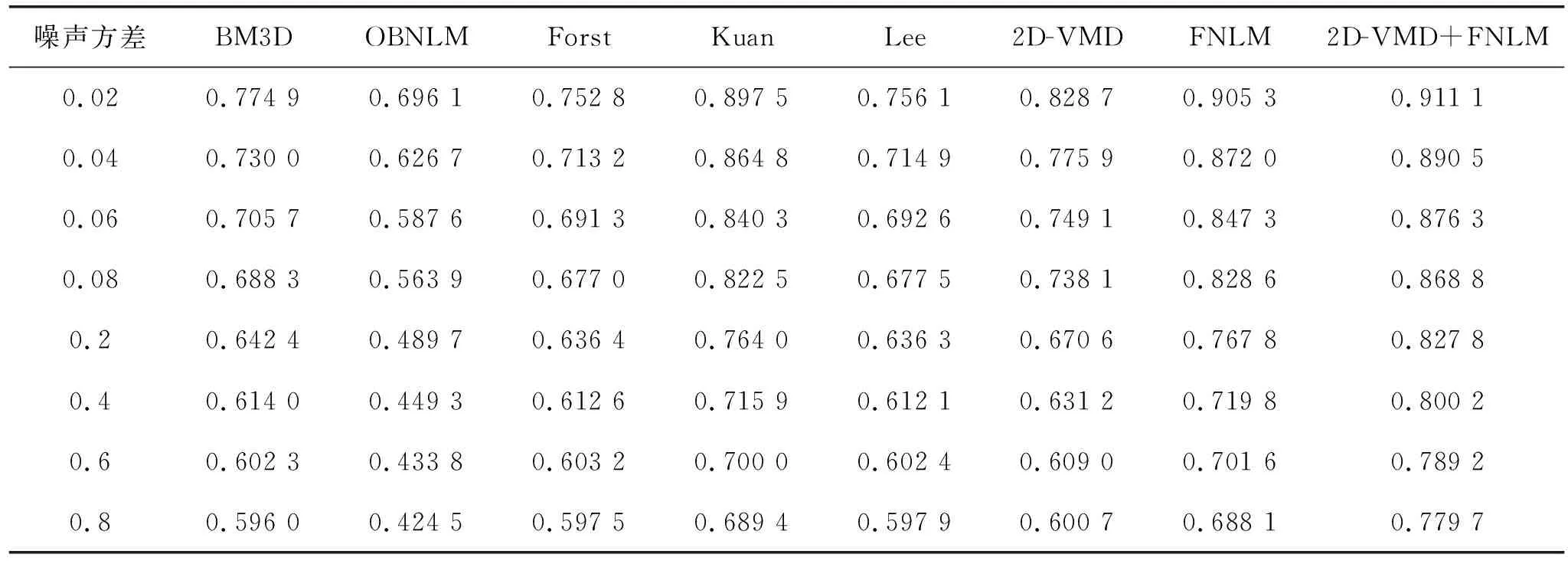
表2 lena图像在不同噪声方差下不同滤波算法的SSIM值
图3是医院提供的真实盆腔超声图像,添加噪声方差为0.2的斑点噪声。PSNR和SSIM评价指标需要使用无噪声的原图作比较求得,但真实的超声图像由于成像机理本身就含有大量噪声,所以PSNR和SSIM不能再作为去噪效果的评价指标。据图3观察,传统Forot滤波、Lee滤波、Kuan滤波以及OBNLM滤波图像中仍含有大量的噪声点,去噪效果并不理想。2D-VMD滤波效果优于以上滤波算法,但仍能看到明显噪声点。BM3D滤波算法滤波效果不如本文算法,图像边缘会产生振铃效应,随着噪声的加大其去噪效果也会大幅度降低,而且算法复杂度较高。FNLM滤波由于噪声方差较大会严重影响相似性权重的计算,导致边缘的破坏。本文算法由于2D-VMD算法先滤除一部分噪声,减小了相似性权重计算的影响,降低了噪声对后续使用FNLM滤波算法对去噪效果和图像边缘的影响。经过对比观察发现,本文算法处理医学超声图像效果优于比其他算法,而且在强噪声背景下去噪效果更加明显。
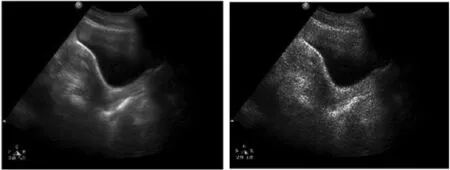
(a) 原图 (b) 噪声图
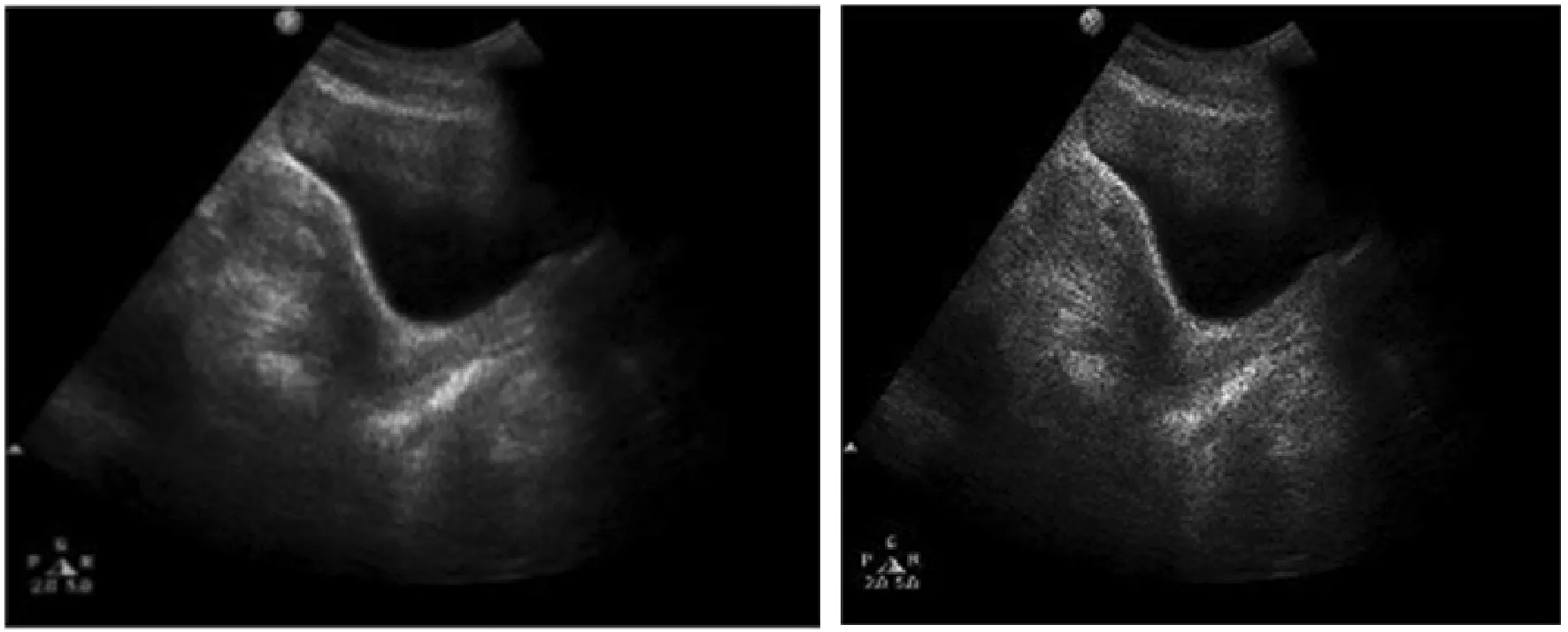
(c) BM3D滤波 (d) OBNLM滤波
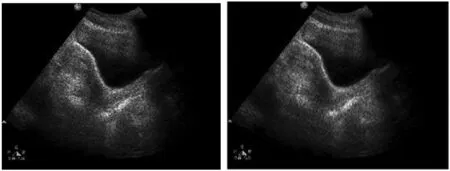
(e) Forst滤波 (f) Kuan滤波
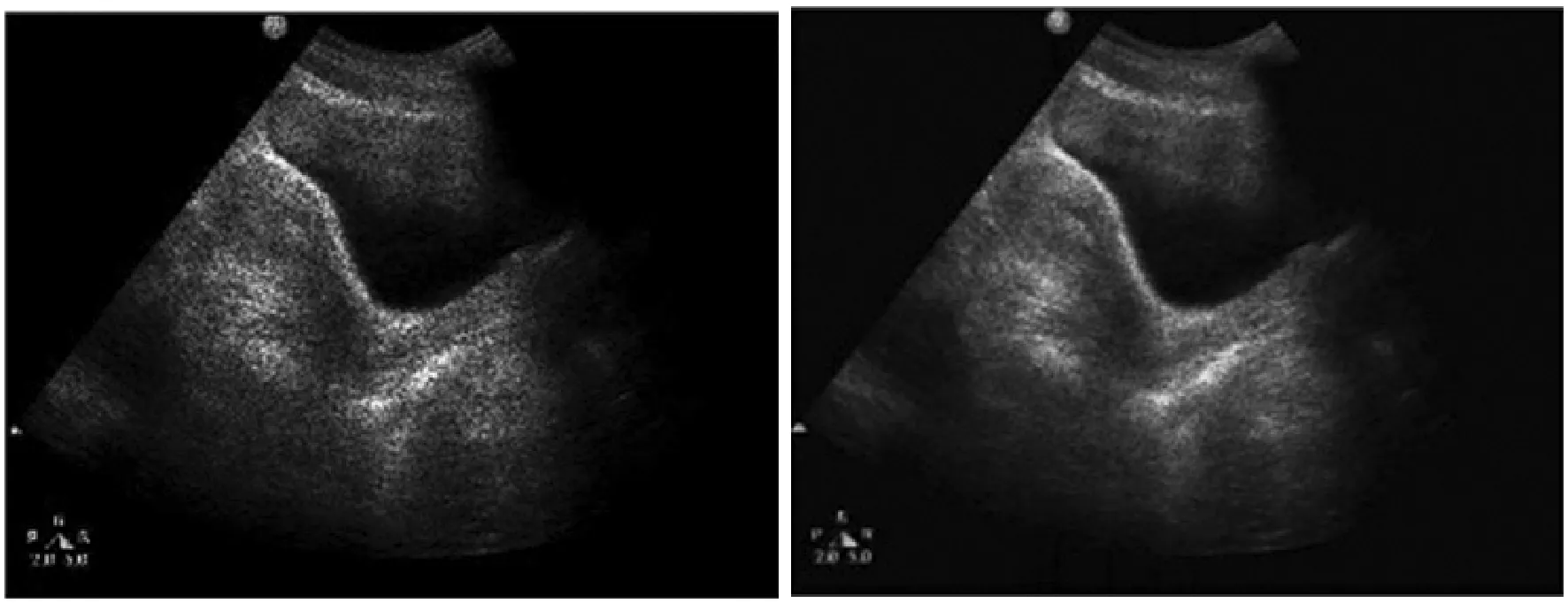
(g) Lee滤波 (h) 2D-VMD滤波
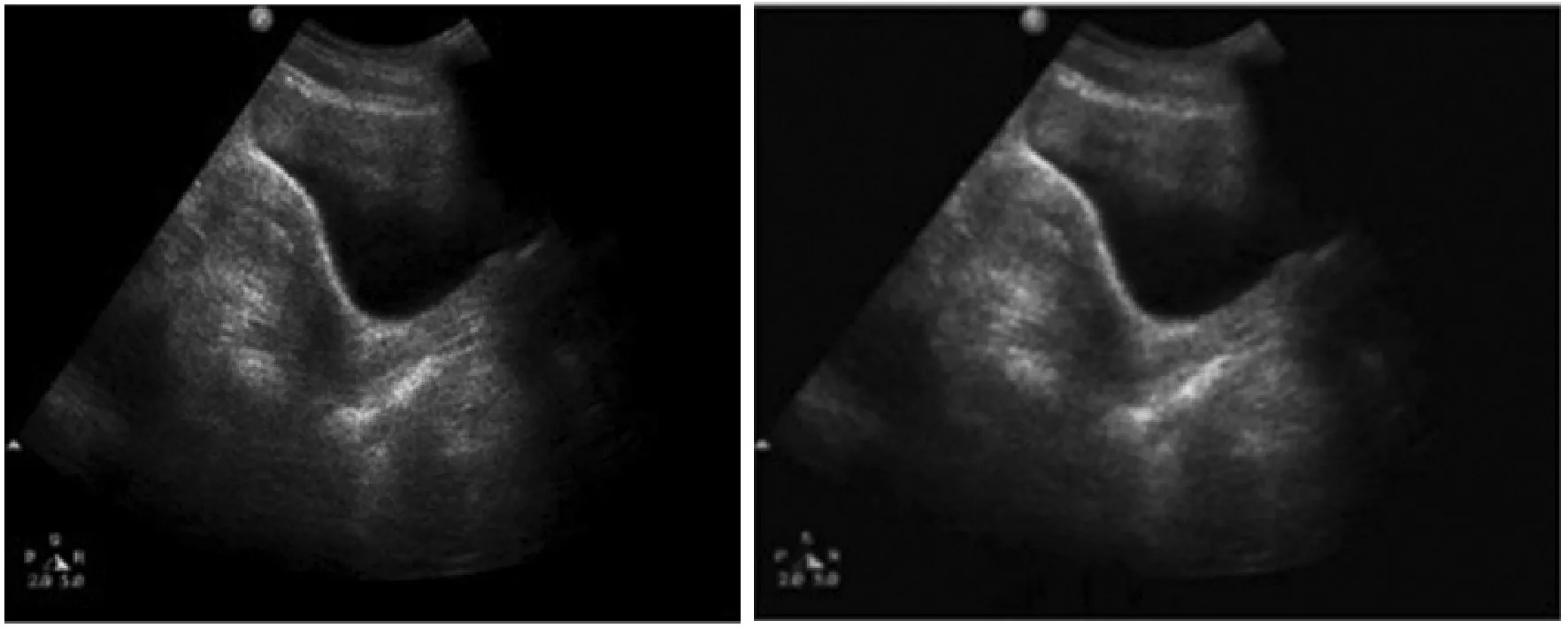
(i) FNLM滤波 (j) 本文算法滤波图3 噪声方差为0.2的盆腔超声图
5 结 语
传统FNLM滤波算法的图像块相似性度量方法没有鲁棒性,仅通过欧氏距离估计灰度值的特点,没有充分考虑到边缘信息的影响。而2D-VMD算法有较好的噪声鲁棒性,弥补了FNLM滤波的缺陷。
根据测试图像lena图像滤波效果发现,本文算法的峰值信噪比和结构相似性均优于其他滤波算法,且高噪声背景下本文算法滤波效果更加明显,真实超声图像滤波实验结果中,本文算法仍能在去噪的同时保留良好的边缘细节。
