基于受限玻尔兹曼机和粗糙集的风速区间概率预测模型

于晓要 李 娜

(商丘工学院 河南 商丘 476000)

0 引 言

近年来,风能作为清洁能源受到了广泛关注,全球风电装机容量逐年增长。风力发电的稳定性和可靠性是需要考虑的关键问题,因此,有必要进行风电预测。由于风电预测依赖于大气气象学和风速,因此提高风速预测的准确性能改善风电预测结果[1]。由于风速数据具有随机性和混沌性,用线性方法预测相当困难[2]。一般预测时间长短与预测准确性呈负相关关系,根据预测时间可分为超短期、短期和中长期预测。

风速预测方法主要有持续性模型、基于气象参数预测、统计学方法和基于机器学习的预测方法等。通常持续性模型对目标函数作简单的平滑假设,未来风速被认为等于预测时间内的风速[3],这是最简单和最经济的风力预测方法。当预测时间范围延长时,持续性模型的性能迅速下降,因此,只适用于超短期预测。数值天气预测(Numerical Weather Prediction,NWP)适用于大规模地区长期预测[4],主要缺点是计算时间和复杂度高,在预测过程中遇到不可测误差会导致严重的偏差,短期预测不可靠。统计学方法旨在找出风速时间序列统计分布规律和随机过程来把握趋势性非平稳变化。统计模型以各种回归预测为主,包括多元线性/非线性回归、自回归(Auto Regressive,AR)、自回归移动平均(Auto Regressive Moving Average,ARMA)、自回归综合移动平均(Auto Regressive Integrated Moving Average,ARIMA)。文献[5]应用多变量ARMA进行逐时风速预测,但由于其中的线性假设,它无法对较长的时间范围给出准确的估计。文献[6]充分考虑风速自身高低及风速变化率对条件方差的影响,提出一种基于ARIMA和广义自回归条件异方差模型的风速预测方法,可快速实现超短期内风速的点预测与区间预测。

近年来,提出的基于机器学习的短期风速预测方法主要有模糊逻辑[7]、人工神经网络[8]和支持向量机(Support Vector Machine,SVM)[9]。人工神经网络(Artificial Neural Network,ANN)应用广泛,它能够捕捉输入数据与预测风速值之间的关系[8]。现有研究提出了前馈神经网络[10]、递归神经网络[11]、径向基函数(Radial Basis Function,RBF)神经网络[12]、自适应小波神经网络[13]和非线性自回归神经网络(nonlinear autoregressive networks,NARNN)[14]用于风速和风力发电预测。基于人工神经网络的预测方法由于能够反映输入输出变量之间复杂的非线性关系,在时序预测中得到了广泛应用。人工智能方法可分为浅层和深度学习模型。前馈神经网络等浅层模型利用单隐层来捕获时间特征,这种模型无法从数据中自动学习无监督的特征。深度学习能够训练多层隐藏计算单元,具有很高的泛化能力。文献[15]将深度叠加自动编码器(Stacked Auto-Encoder,SAE)应用于短期风电预测。文献[16]采用深度置信网络(Deep Belief Network,DBN)进行短期风场预测。DBN和SAE可利用无监督的数据来初始化模型参数。文献[17]指出当深度网络的验证错误率很小时,即使网络容量大、复杂度高、最小值很小,也能保证网络具有很好的泛化能力。

各种回归方法所作的预测具有不确定性[12],现有方法通常假设输入变量服从伯努利分布,没有对实值数据建模,为此,本文提出一种新的区间概率分布学习模型(IPDL),基于受限玻尔兹曼机(Restricted Boltzmann Machines,RBM)[18]和粗糙集理论[19]从底层输入时间序列中获取区间无监督特征。在风速时间序列数据集中,通过降低能量函数,同时增加观测输入向量的概率来学习概率分布函数。可见层和隐藏层的条件概率可以很容易地分解为简单的因子,计算量小。此外,为了有效地训练IPDL模型,提出一种基于对比散度和Gibbs抽样的无监督学习算法。在此基础上,提出一种具有实值输入向量的区间深度置信网络(IDBN),利用IPDL来获得风场数据的概率分布。利用IDBN和FT2IS设计一种混合风速预测方法,称为深度混合(Deep Hybrid,DH)方法,用于未来风速值的有监督回归。与基于监督回归的ANN、SVR和模糊系统等人工智能方法不同,特征提取不需要关于风力数据的先验知识。此外,仿真结果表明,该方法能够准确地处理输入数据的不确定性。

1 风速数据分析

风速是具有许多波动的非线性时间序列,因此,基于平滑性假设的方法存在诸多不足。本文基于数据驱动,从输入的风速数据中捕捉统计特征。文献[19]应用自相关函数(Autocorrelation Function,ACF)来获得不同时间样本下风速时间序列的相关性。由于ACF只能计算一个变量与自身的线性相关性,引入互信息(Mutual Information,MI)处理风速数据高度非线性。假设两个随机变量X、Y,X的熵由H(X)表示,联合熵H(X,Y)用于计算其不确定度。用条件熵H(Y|X)=H(X,Y)-H(X)表示在已知变量X时Y的不确定度。两个随机变量之间的MI是一个非线性函数,用于测量已知一个变量时,另一变量的信息。MI由I(X,Y)=H(Y)-H(Y|X)计算。t时间的风速值为v(t),计算v(t-l+1)和v(t+1)之间的MI作为时滞。将MI大于阈值0的时滞对应的风速数据作为算法的输入集,以突出风速时间序列中的相关性。

2 区间概率分布学习

2.1 粗糙特征提取

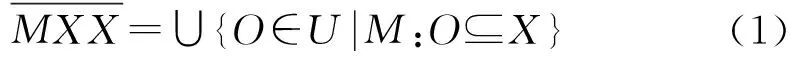
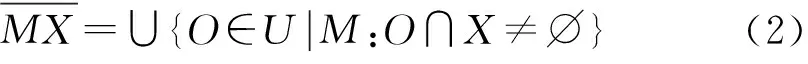
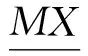
2.2 区间分布学习模型

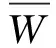
式中:指数1≤j≤H和1≤k≤D分别对应隐层单元和可见单元。定义联合概率分布函数为:

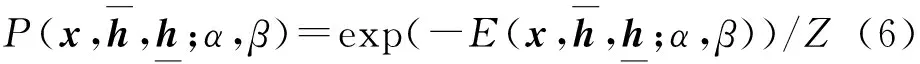
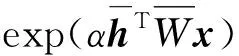
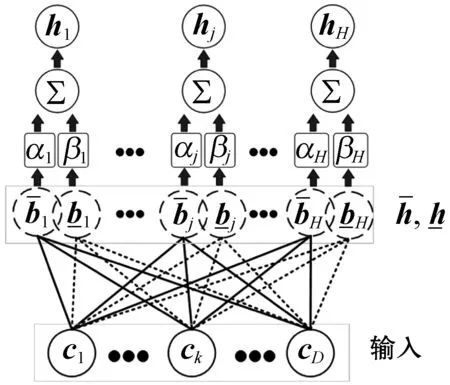
图1 含输入的区间概率分布学习模型结构

2.3 IPDL推论

隐藏向量h给定输入x的概率为:

(8)

由于隐藏层内的节点是相互独立的,所以式(8)的分母可写成与一个特定隐藏单元对应的单个表达式的乘积:

那么,式(8)的条件概率可以改写为:

其中,给定输入x和系数αj的上界隐藏条件概率为:

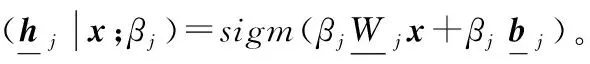
2.4 IPDL学习算法

假设上下界隐藏单元权重相同αj=1-βj=0.5,则式(11)-式(12)中条件概率的前馈计算如下:

利用训练集Dtr={x(t)|1≤t≤T}中的T个数据样本训练上界和下界参数,无监督对数概率损失函数为:

式中:J(Dtr)是在数据集Dtr上定义的监督误差函数。为了更新参数θ,关于θ的随机梯度计算如下:

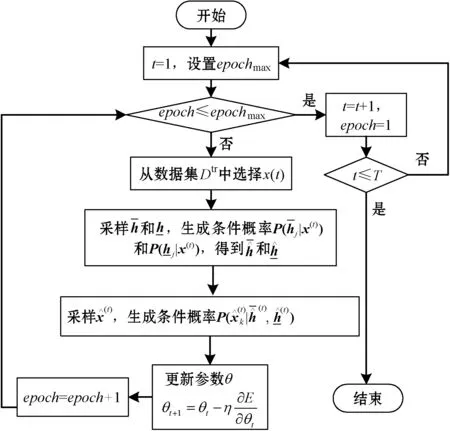
图2 IPDL算法流程

为了采用式(15)调整IPDL,通过下式对式(15)的期望运算进行估计:

其中,上界和下界隐藏样本的计算方式为:

(19)

式中:II(·)是指示函数。

3 深度混合风速预测方法

该方法由带粗糙模式识别的区间深度置信网络和模糊II型推理系统组成。图3给出了所提DH模型的结构。首先,将基于互信息的特征选择算法应用于历史风速时序数据,并选择与未来数据更相关的时间滞后作为D维输入向量〈x1,x2,…,xD〉。为了从风速分布中提取非线性特征,提出一种基于实值输入变量IPDL生成模型的区间深度置信网络。IDBN包含L个IPDL,这些IPDL堆叠在一起以提取时间特征。通过最大化IPDL模型的对数似然来学习这些特征,作为一种无监督的方法来初始化多层神经网络的权值和偏差。初始化过程也可以看作是一个正则化过程,随机初始化的参数被移动到一个良好的初始子空间。从IDBN接收到的每个数据样本的结果被馈送到高斯隶属度函数,其区间标准差将被模糊II型TSK推理系统所使用。采用TSK作为回归模型,对未来时间序列值进行了拟合。

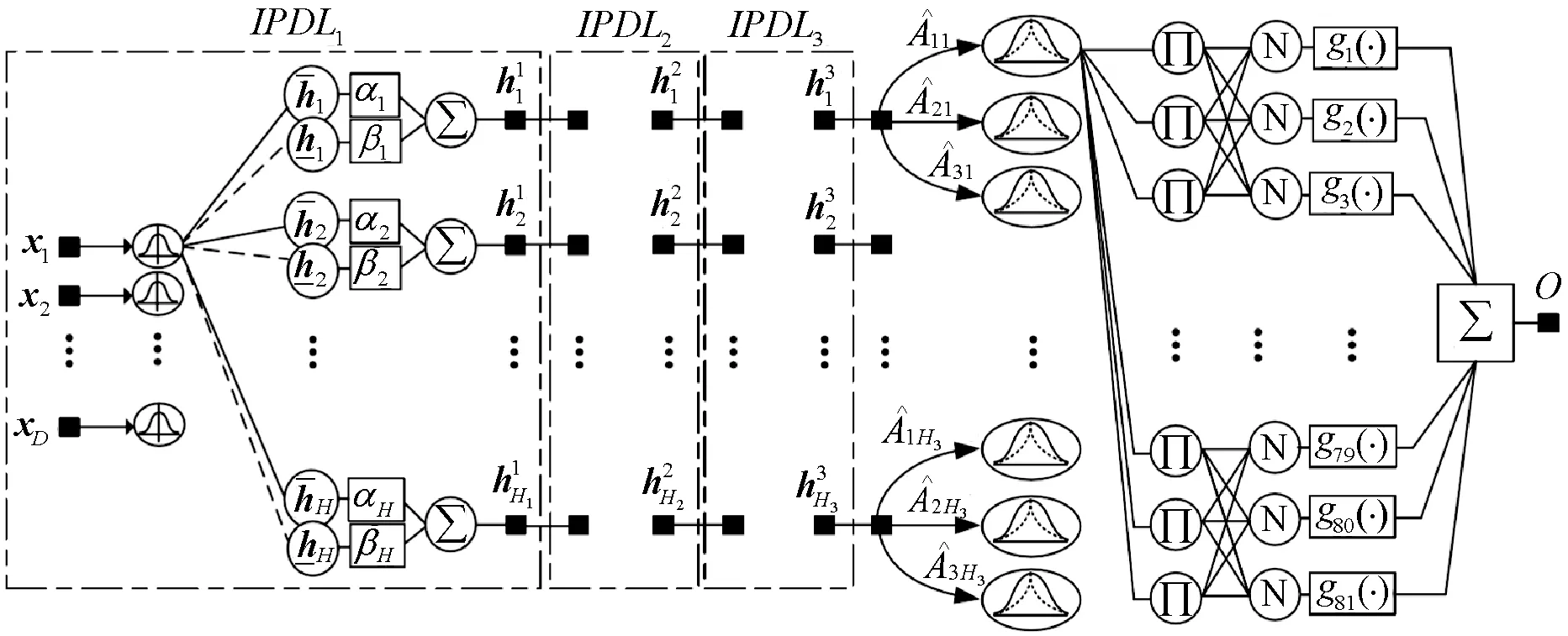
图3 L=3的DH算法结构

3.1 深度混合方法的结构

3.1.1无监督概率分布学习

图3给出了所提DH模型的结构。首先,利用提出的IPDL模型和TSK模糊系统设计了一个IDBN。与经典的DBN相比,为了更准确地了解实值风力数据的概率密度,本文考虑了初始IPDL的实值输入单元。IPDL是连续训练的,无须监控,使用原始风速时间序列,无须预处理。因此,不需要任何先验知识来从时间序列中提取特征。每个IPDL使用式(17)-式(19)进行训练。考虑到IDBN中IPDL模型的个数为L,网络应连续地训练L个模型。第一个IPDL的输入IPDL1是可见的时间序列数据x=〈x1,x2,…,xD〉。该模型从输入数据中学习特征。第i个IPDL接收从其先前训练的IPDLi-1中获得的特征hi-1。

3.1.2监督IDBN调整

IDBN在第L层之后应用线性回归进行微调,期望的预测输出作为监督信号。初始隶属度函数的参数是通过聚类从IDBN得到的。在此阶段采用有监督平方误差损失函数。

3.1.3FT2IS学习和DH微调

混合预测器采用端到端的随机梯度下降(StochasticGradient Descent,SGD)方法进行微调。由于该网络的输出与IPDL模型的上、下界参数和FT2IS模型是可微的,因此能以端到端的方式有效地训练整个系统。图2中提出的学习过程作为参数的正则化技术,有助于IPDL找到DH的区间权重和偏差的精确初始化。与文献[20]中随机初始化的模糊网络相比,该框架利用生成的IPDL对模糊系统的隶属度函数进行最优初始化,更准确地处理了风力数据的不确定性。

3.2 实值数据的深度置信网络

由于对时间序列信号采用伯努利分布对风速预测不够准确。因此,提出实值输入向量以更高的估计精度模拟风速分布。所以,新的能量函数定义为:

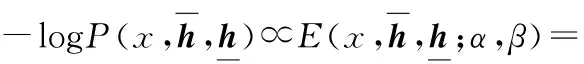
式中:σ是高斯可见层的标准偏差向量x=〈x1,x2,…,xD〉。xi的条件概率计算方法如下:

为了初始化IDBN的权值和偏差参数,将模型的对数似然最大化为σi=1,以便于训练过程中应用马尔可夫链蒙特卡罗计算式(15)中的期望值。

3.3 模糊回归法

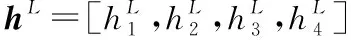
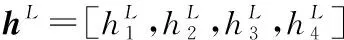
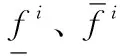
式中:*是用作T范数函数的乘积算子。第i条规则的触发可以表示为:

通过式(27)计算回归输出:

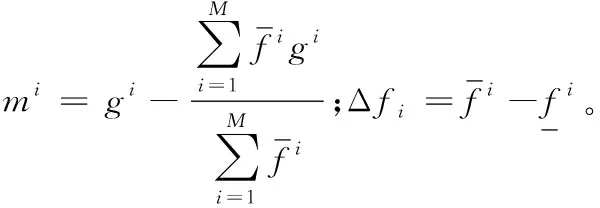
3.4 监督端到端训练

在对IDBN进行预训练后,得到hL向量,并将K-Means算法作为无监督聚类方法用于激活hL,以确定高斯隶属函数的初始均值。种群数目被设置为所考虑的成员函数的数目。监督误差函数为:

式中:T是训练样本数;Ot是DH输出;Vt是第t次训练样本的输出。EReg是正则化误差项:

式中:0<λ<1是正则化系数。为了提高SGD的训练速度,特别是实值IDBN的自由参数,Jsup相对于后续部分的自由参数的梯度为:

式中:et=Ot-Vt是第t个训练样本的误差。隶属函数的均值和区间标准差参数的梯度计算如下:

式中:M是每个FT2IS输入的隶属函数数目,因此,MHL是在所提系统中定义的II类规则的总数。为了更新粗糙特征(区间权重和IDBN的偏差),关于每个粗糙单元的上下限参数Jsup的偏导数根据式(19)类似公式计算。所提出模型相对于输入可微,因此,可以端到端地调整整个深度网络参数。

4 算例分析

4.1 数据集

算例选用了美国国家可再生能源实验室统计的某地区风力数据集[21]。数据集中的风速数据有3年的风速值,连续历史样本之间的间隔为10 min,每年包含52 560个数据,有足够的数据可用于训练和测试。DH方法使用离线和在线两种方式进行训练。用TS表示训练集,它包含M个样本(i),1≤i≤M;用TT表示测试集,它包含N个样本(j),1≤j≤N。首先,模型在TS离线训练,在SGD的每个训练时段对TS的每个样本使用式(30)-式(31)更新参数。然后,对模型进行在线训练,即模型在N次迭代中逐个观察TT中的值。每次迭代时,都会向DH模型提供一个样本TT(j),并计算相应误差。在随后的迭代中将TT(j+1)输入到前一模型,其误差被于式(30)-式(31)更新模型。前两年数据集用于训练,第三年数据用于测试;从第二年每个季度中数据集选择15%用于测试。在连续三个训练阶段,当验证均方根误差(Root Mean Square Error,RMSE)的相对变化小于5%时,训练停止。图4给出了第二年高度变化的风速时间序列。Kolmogorov-Smirnov、Anderson-Darling和卡方检验表明,Weibull概率分布的平均值为7.32 m/s,形状因子为2.15。

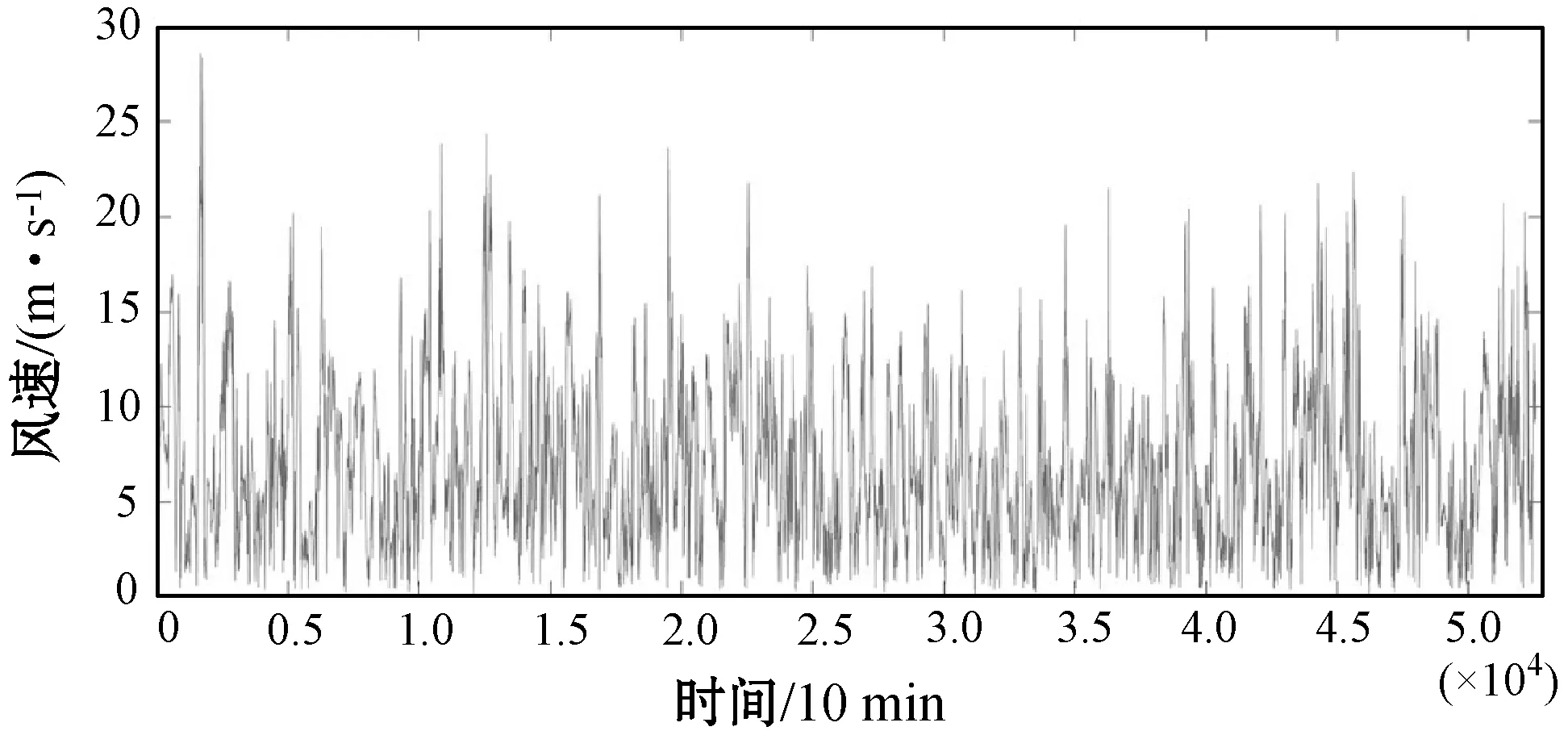
图4 第二年风速值

4.2 输入变量选择

图5给出了滞后l=1到l=100的MI。结果表明,风速测量值之间的相关性随着时滞的增大而减小。选择τ=0.4的时间滞后相对应的风速数据作为输入集,以突出显示风速数据之间的相关性。假设模型在t时间预测未来风速值,输入集是24+23=47维向量〈v(t-23),Δv(t-22),v(t-22),…,v(t)〉,风速序列差为Δv(t)=v(t)-v(t-1)。

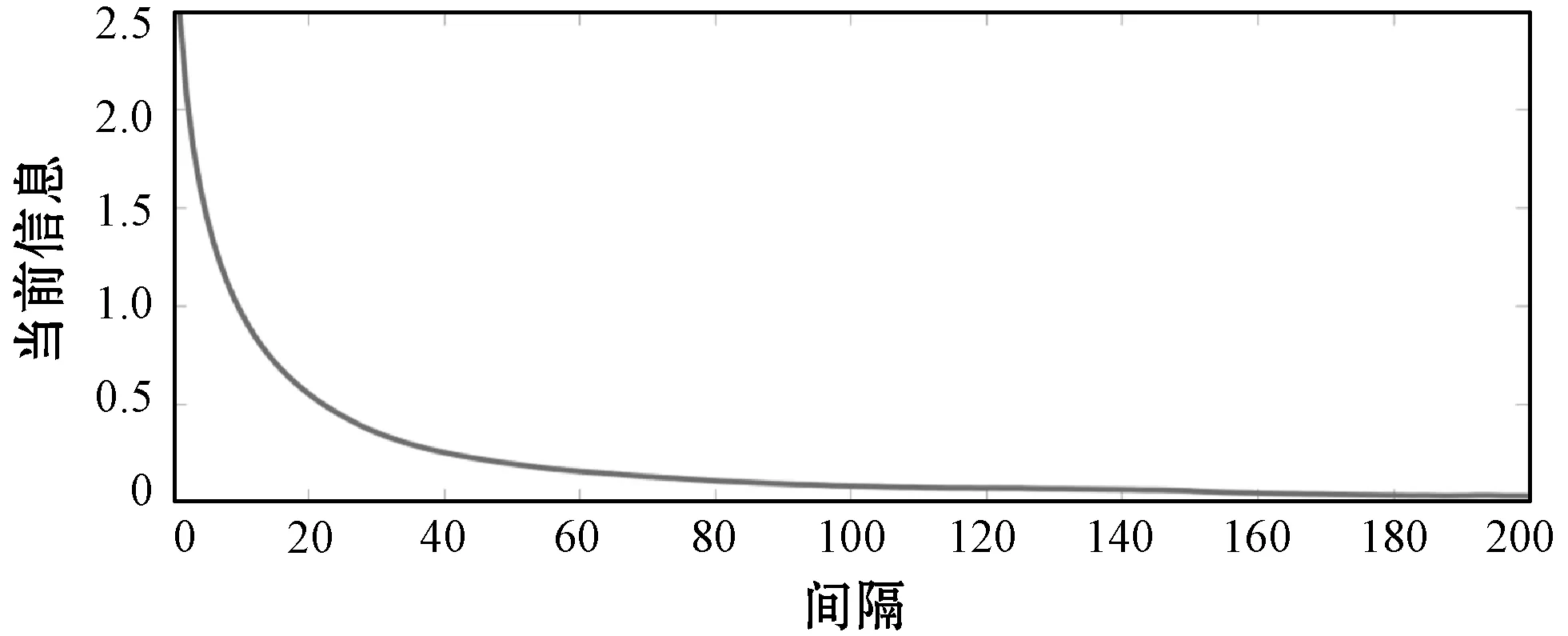
图5 第二年数据集不同时差的互信息

4.3 评估标准

采用均方根误差RMSE和绝对百分比平均误差(the Mean Absolute Percentage Error,MAPE)对模型进行评价,计算如下:

式中:err(n)=t(n)-o(n)是第n个样本的测试误差,t(n)是目标值,o(n)是输出值。

4.4 算例模拟设置

提出的DH模型以互信息产生的47维输入向量作为特征选择算法。每一层的激活单元的数目从φ={5,10,15,…,45}中选择。IDBN可以包含2到5个IPDL作为混合模型的初始隐藏层。底层迭代次数是避免过度拟合的重要因素,考虑最多80次迭代来训练模型。此外,当验证过程在5个阶段的变化小于等于0.05的阈值时,满足训练过程的停止准则。训练率η和动量项系数设为0.5。L2正则化的权重衰减参数λ从集合{0.2,0.3,0.4,0.5,0.6}中选择。最优λ对应于训练过程结束时的最小验证误差。

为了确定IDBN的最优结构(确定DH算法中L值),对固定集φ进行随机搜索。根据100次运行的平均验证误差选择最优模型。图6给出了随着IPDL数量的增加,1 h、10 h和24 h前风速预测的验证RMSE。可以看出,对于提前1 h预测,具有2个IPDL的IDBN存在最小误差。当提前预测时间延长到10 h,IPDL数量为3时误差最小。随着预测复杂性的增加,IPDL的最优数目也随之增加。对于提前24 h的预测,具有4个IPDL的IDBN具有最小的误差率。更多的IPDL会导致过度拟合问题,而较少的隐藏层会降低DH的处理能力。

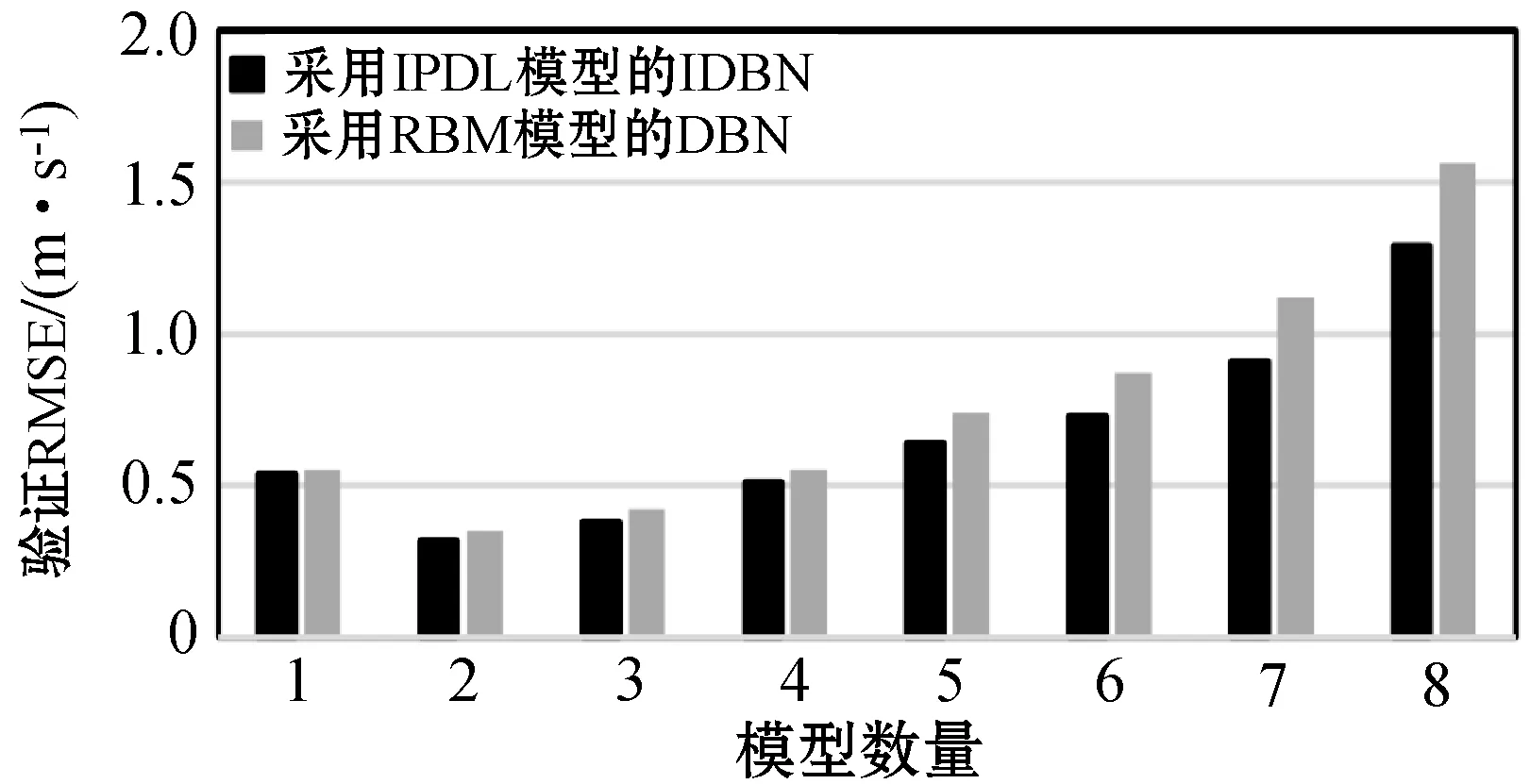
(a) 提前1 h预测结果

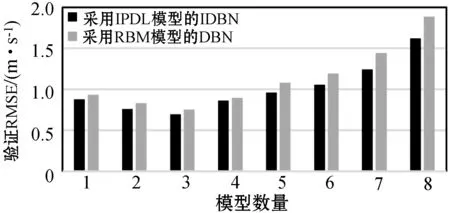
(b) 提前10 h预测结果

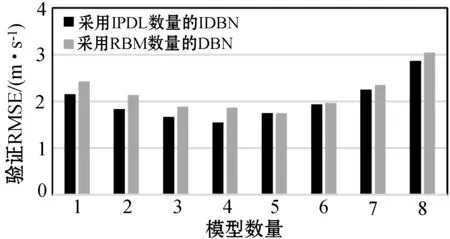
(c) 提前24 h预测结果图6 RMSE验证结果

为了将提出的IPDL与经典DBN进行多步预测,训练了一个带有Bernoulli-RBM的DBN来代替DH中提出的IDBN模型。如图6所示,与DBN模型相比,IDBN在验证集误差更小。而且,DBN结构需要更多的隐藏层。例如,在提前24 h预测中,Bernoulli-DBN需要5个生成模型(RBM)才能达到最优解,而所提出的体系结构由4个IPDL模型组成。因此,利用所提出的区间分布学习方法,可以减少深度置信网络的计算负担,同时获得更好的精度。FT2IS回归模型包含4个输入变量,对于每个输入,有3个高斯隶属函数,规则的数目是34=81。将3个聚类的K-Means算法应用于IDBN特征,以确定隶属函数的初始均值。这些函数的标准差和自由参数在[0.01,0.2]中随机选取。

4.5 数值结果与比较

本文提出的DH方法与持续性(Persistence,PR)模型[22]在超短期及短期风速预测中进行了比较。此外,还将该模型与现有文献中的单一模型和混合方法进行了比较。单一模型应用单一回归架构来预测,为了显示深度学习对风数据回归的影响,将基于浅层神经网络的方法,包括前馈神经网络FFNN[10]、时滞神经网络TDNN[11]和非线性自回归神经网络NARNN[12]与本文方法进行了比较。此外,将所提模型与当前SAE[15]和深度学习方法DBN[16]进行了比较。

为了提高预测精度,混合模型采用了多重风特征提取和回归方法。在本文中,将DH模型与混合E-GA-APSO-WNN模型[23]进行了比较,该模型应用集成经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)来降低风速时序数据中的噪声,以及将遗传算法(Genetic Algorithm,GA)与粒子群优化(Algorithm of Particle Swarm Optimization,APSO)相结合作为小波神经网络WNN参数优化方法。并与文献[24]提出的基于特征选择和参数优化的混合回溯搜索算法HBSA的混合极值学习机ELM短期风速预测模型进行了比较。文献[24]中提出的ELM-HBSA模型有效地捕捉了风速信号的非线性特征,并优于ARIMA和SVR两种预测模型。

4.5.1深度学习与浅层特征学习的比较

表1和表2给出了10 min至3 h前风速预测的RMSE和MAPE,并与浅层和深层单模型方法进行了比较。RMSE、MAPE一般随着预测时间的延长而增加。PR方法可产生准确的短期预测结果,提前10 min的RMSE为0.625 m/s,提前3 h的RMSE为2.785 m/s。提前10 min预测的平均相对误差为10.983,在提前3 h预测中达到30.174。因此,将PR不适用于长期预测。

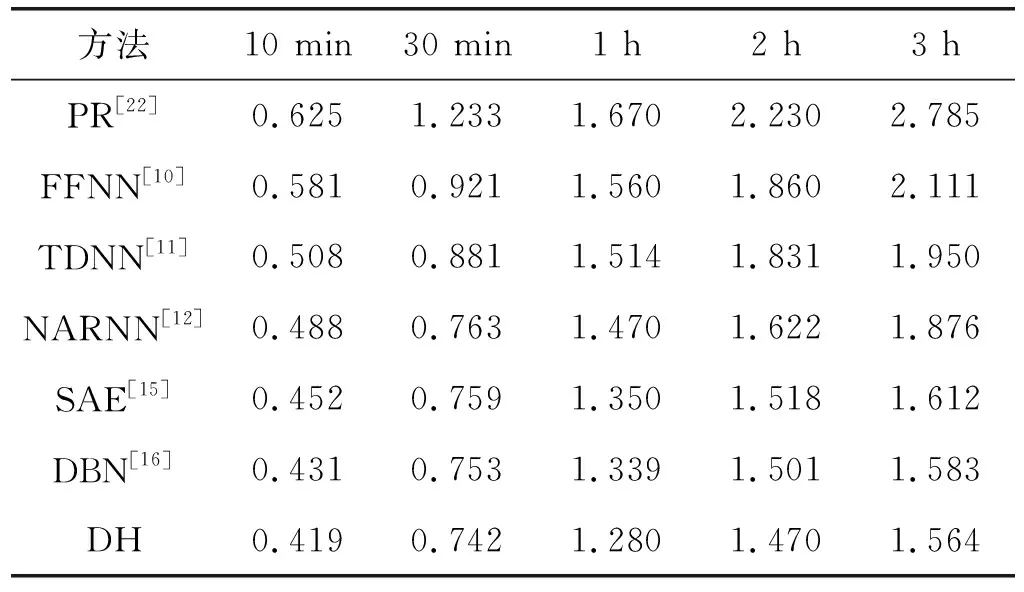
表1 单一模型不同时段的RMSE 单位:m/s

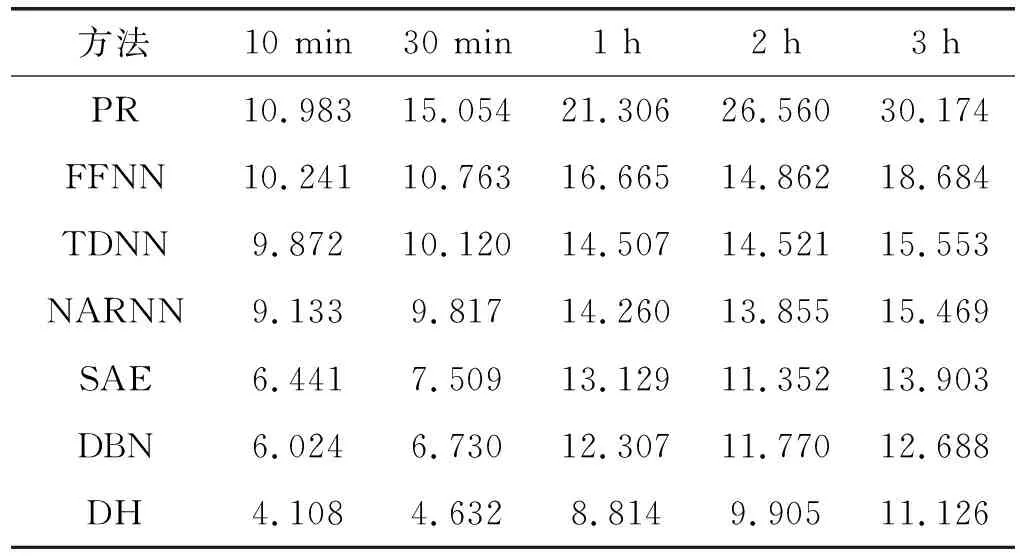
表2 单一模型不同时段的MAPE

与PR相比,FFNN得到了更好的结果。在提前10 min预测中,FFNN的RMSE较PR提高了7.04%;对于提前3 h的预测,提高了24.20%。PR在提前3 h预测中性能较差是由于该模型只有简单平滑假设。TDNN模型和NARNN模型都优于FFNN模型,因为这些方法可以在捕获数据的时间特征的同时对时序数据的序列属性进行建模。与FFNN相比,TDNN的RMSE和MAPE分别提高了5.80%和8.32%。NARNN的RMSE和MAPE结果分别比FFNN好12.56%和11.60%。与FFNN和TDNN模型相比,NARNN是最好的浅层神经结构。将NARNN与深度网络SAE进行比较,结果表明,与NARNN相比,SAE的RMSE和MAPE分别改善了7.23%、17.82%。当采用DBN模型时,RMSE和MAPE的改善效果分别提高了8.99%和22.44%。由于具有更多的非线性隐藏层和捕捉输入分布,使得DBN和SAE具有更好的泛化能力,有助于获得更精确的风速预测。与文献[15]中提出的SAE相比,DBN具有更好的准确性,因为无监督特征提取是通过RBM完成的,可以更好地获得输入分布。

与DBN和SAE相比,该混合模型得到了更为精确的结果。与文献[16]提出的DBN相比,本文模型使RMSE降低了2.7%,MAPE降低了23.90%。基于DBN的混合模型的改进在于:(1) 利用所提出的区间特征和FI2IS进行回归,通过从时间序列中获取区间来处理风速数据中存在的不确定性;(2) 采用实值输入单元,与SAE和DBN相比,具有更高的精度。图7给出了第三年中72个样本的提前3 h预测的NARNN和DBN预测结果与实际风速。可以看出,DBN通过学习风数据概率分布,改进了NARNN的结果。图8给出了文献[16]中提出的采用RBM的DBN与本文方法的比较结果。可以看出,DBN的最大绝对误差值为0.98 m/s,IDBN模型将此误差减小到0.43 m/s,产生更准确的结果。这是因为:(1) 所提出的IPDL模型从数据中学习到一个区间隐藏关系;(2) 与使用二进制输入单元的DBN相比,本文模型采用从实值数据中学习的实值输入变量。

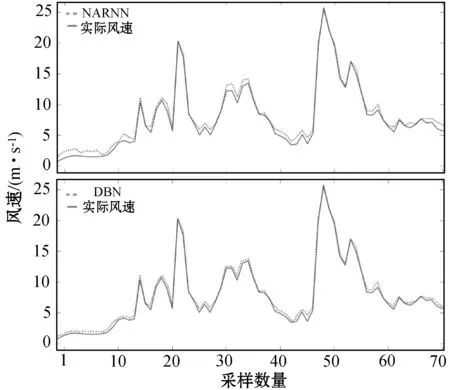
图7 第三年某日提前3 h预测值与实际风速

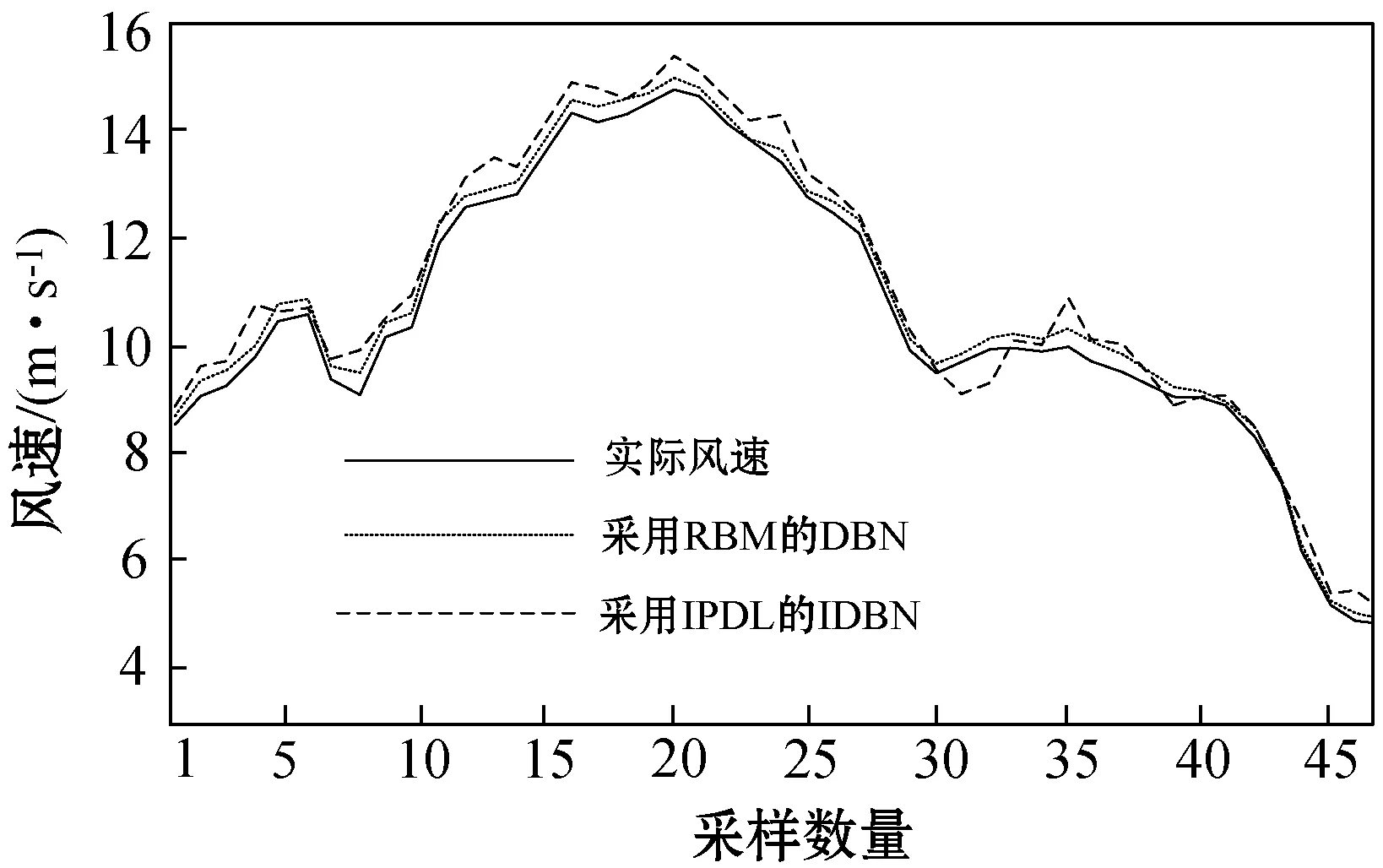
图8 第三年某日测试样本与提前1 h预测结果比较

4.5.2混合方法的比较

表3和表4给出了所提DH模型的RMSE和MAPE,以及E-GA-apsown和ELM-HBSA两种基础混合方法的结果。两种基础混合方法都采用信号分解来降低噪声,而DH模型从数据中获取区间特征,以处理风数据的不确定性。与ELM-HBSA相比,E-GA-APSO-WNN在提前1 h和3 h预测中的MAPE分别改善了10.39%和13.61%。DH模型优于E-GA-APSO-WNN。对于超短期(提前10 min)的预测,DH模型相对于E-GA-APSO-WNN的MAPE结果改善了45.96%,这是由于提出的深度网络采用了自动无监督深度特征提取。在提前3 h预测中,与ELM-HBSA和E-GA-APSO-WNN相比,DH模型的MAPE分别减少21.19%和8.79%。

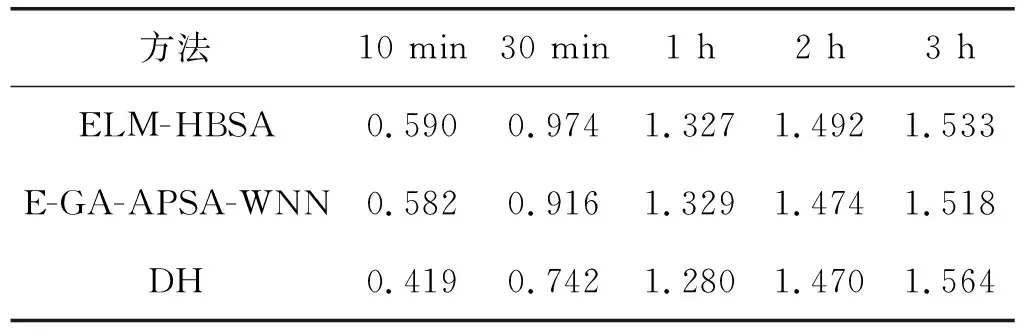
表3 混合模型不同时段的RMSE 单位:m/s

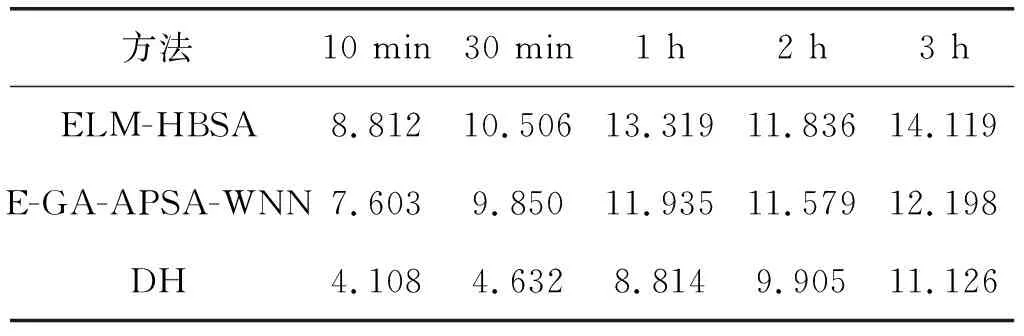
表4 混合模型不同时段的MAPE

图9和图10分别给出了从提前1 h预测到提前24 h预测的所有单一模型和混合方法的RMSE和MAPE结果。与混合方法相比,SAE和DBN在提前1 h到提前7 h预测中具有较好的精度;但是,对于较大的预测时间步长,混合方法在RMSE和MAPE中都有显著的改进。当提前预测时间超过5 h时,所提DH模型的性能明显优于E-GA-APSO-WNN和ELM-HBSA。

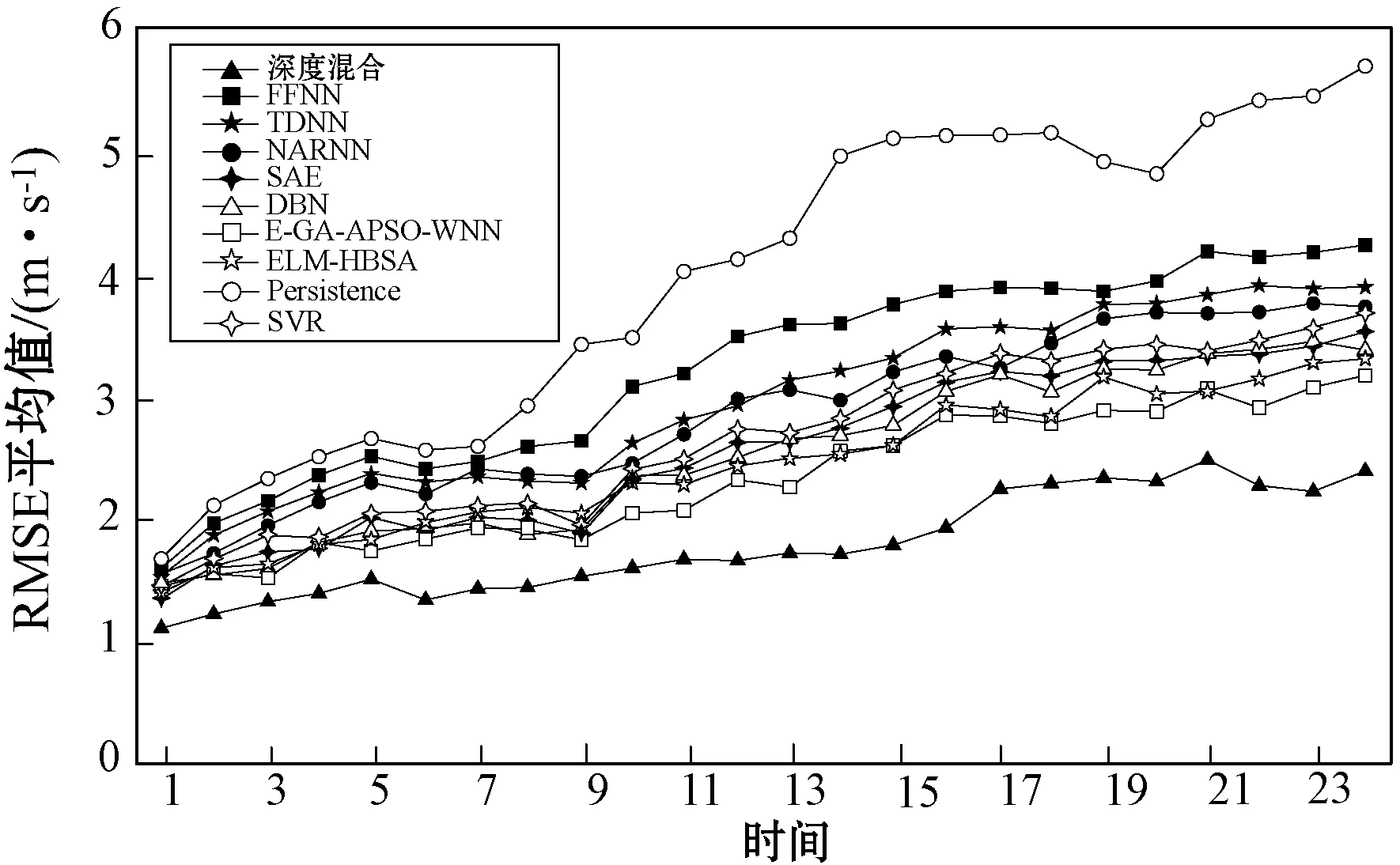
图9 1 h至24 h预测的各模型平均RMSE结果

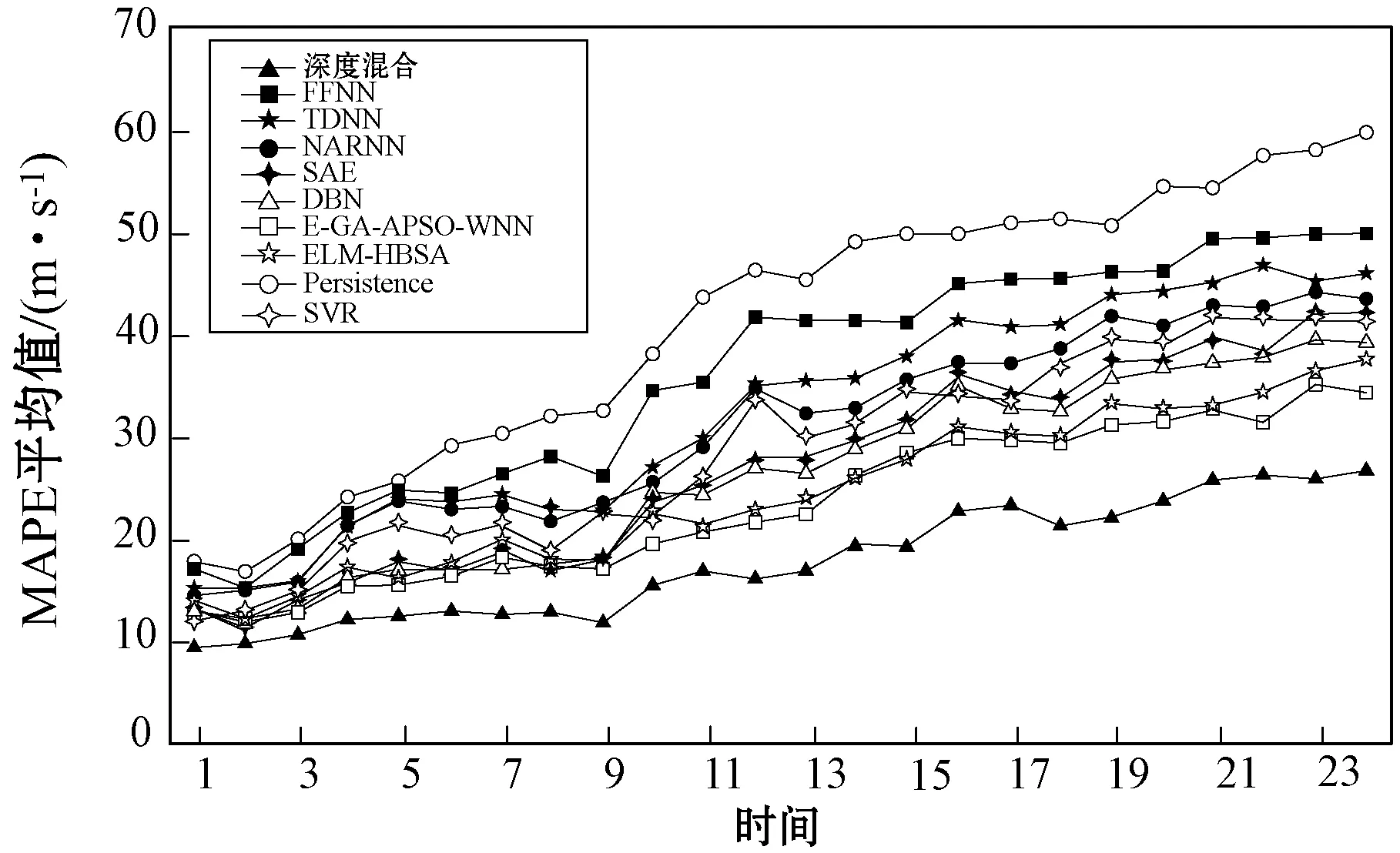
图10 1 h至24 h预测的各模型平均MAPE结果

4.5.3不确定性对模型性能的影响

为了说明风速数据不确定性对模型性能的影响,采用两个扩展的DH模型作为基线,分别为:(1) DHdense采用RBMs代替IPDL模型,为了研究区间特征学习的效果,将本文提出的DH方法与该模型进行了比较;(2) DHTypeI采用模糊I型推理系统代替FT2IS回归模型,本文提出的DH方法与该模型进行了比较,研究了从深度网络中捕获区间II型规则的效果。在不同不确定性条件下,将基线与DH模型进行了比较。根据文献[15]对风速预测模型的鲁棒性实验,每个风速测试样本v考虑高斯噪声Gauss(μ,σ2),μ=0,σ=0.1v。图11给出了DH、DHdense和DHTypeI每小时绝对预测误差的盒须图。与DHdense和DHTypeI对应的框的最小值、中值和最大值都小于采用DH方法相应的值。

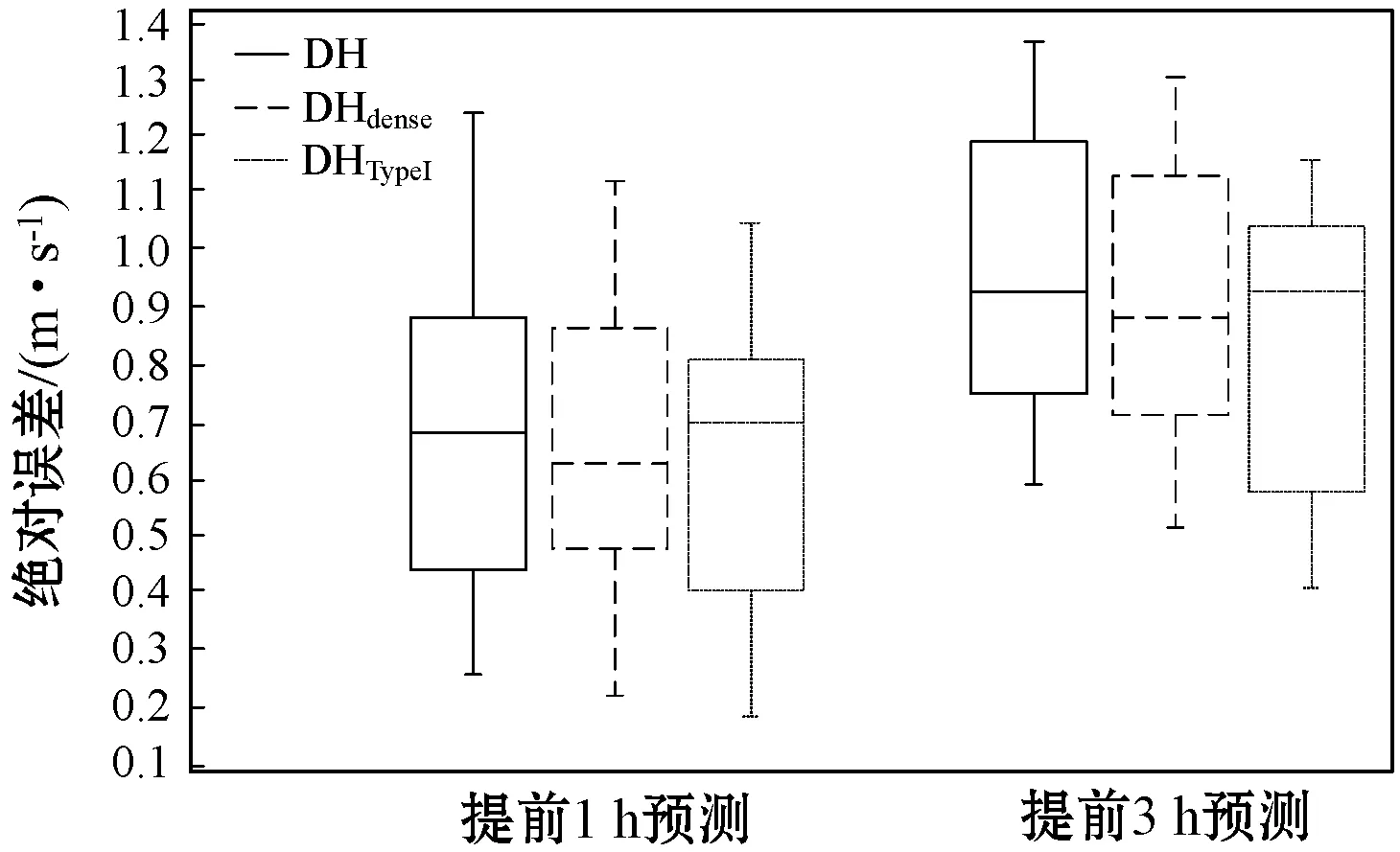
图11 DH、DHdense和DHTypeI每小时绝对预测误差

可以看出,所测数据均未出现异常点。提前1 h预测时,DH每小时绝对预测误差为1.25 m/s、DHdense每小时绝对预测误差为1.11 m/s,DHTypeI每小时绝对预测误差为1.05 m/s。根据提前1 h预测结果可知,DHTypeI的风速数据不确定性对模型性能的影响较小,整体情况比较稳定。提前3 h预测时,DH每小时绝对预测误差为1.37 m/s、DHdense每小时绝对预测误差为1.31 m/s,DHTypeI每小时绝对预测误差为1.15 m/s。根据提前3 h预测结果可知,DHTypeI的不平衡数据较少,整体情况比较稳定。

4.5.4IPDL与RBM的比较

为对所提IPDL方法和RBM进行比较,定义了两个基线:(1) IPDLreg模型包括IPDL和线性回归模型;(2) RBMreg包括IPDL和线性回归模型。图12比较了IPDLreg和RBMreg在测试RMSE方面的性能。如图6所示,当预测时间范围延长时,需要具有更多隐藏层的更复杂网络来获得高精度;然而,具有太多的层将由于梯度而降低模型性能。在图12中,IPDLreg在搜索空间的更宽区域中具有更低的测试RMSE,性能更好,IPDLreg对增加或减少层的数量不太敏感。但是,RBMreg的性能更多地取决于隐藏层的数量。此外,与RBMreg相比,IPDLreg的精度更高,这表明了本文方法相对于RBM的优越性。

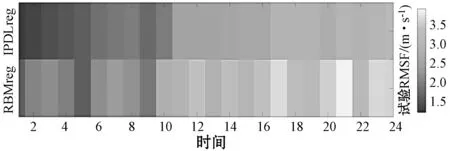
图12 多时段IPDLreg与RBMreg的RMSE比较

4.5.5运行时间分析

图13给出了使用不同下降梯度的DH的离线训练时间。算例在一个多GPU计算机系统上实现,该系统有两个NVIDIA GTX980图形卡和一个4.2 GHz的四核处理器。可以看出,离线训练时间随着时间范围的延长而增加,这是因为隐藏层的数量随着相应回归问题的复杂性而增加。本文方法适用于短期风速预测。对于时间范围小于10 min的预测,在将模型用于实际预测之前,可以使用历史数据离线调整模型。

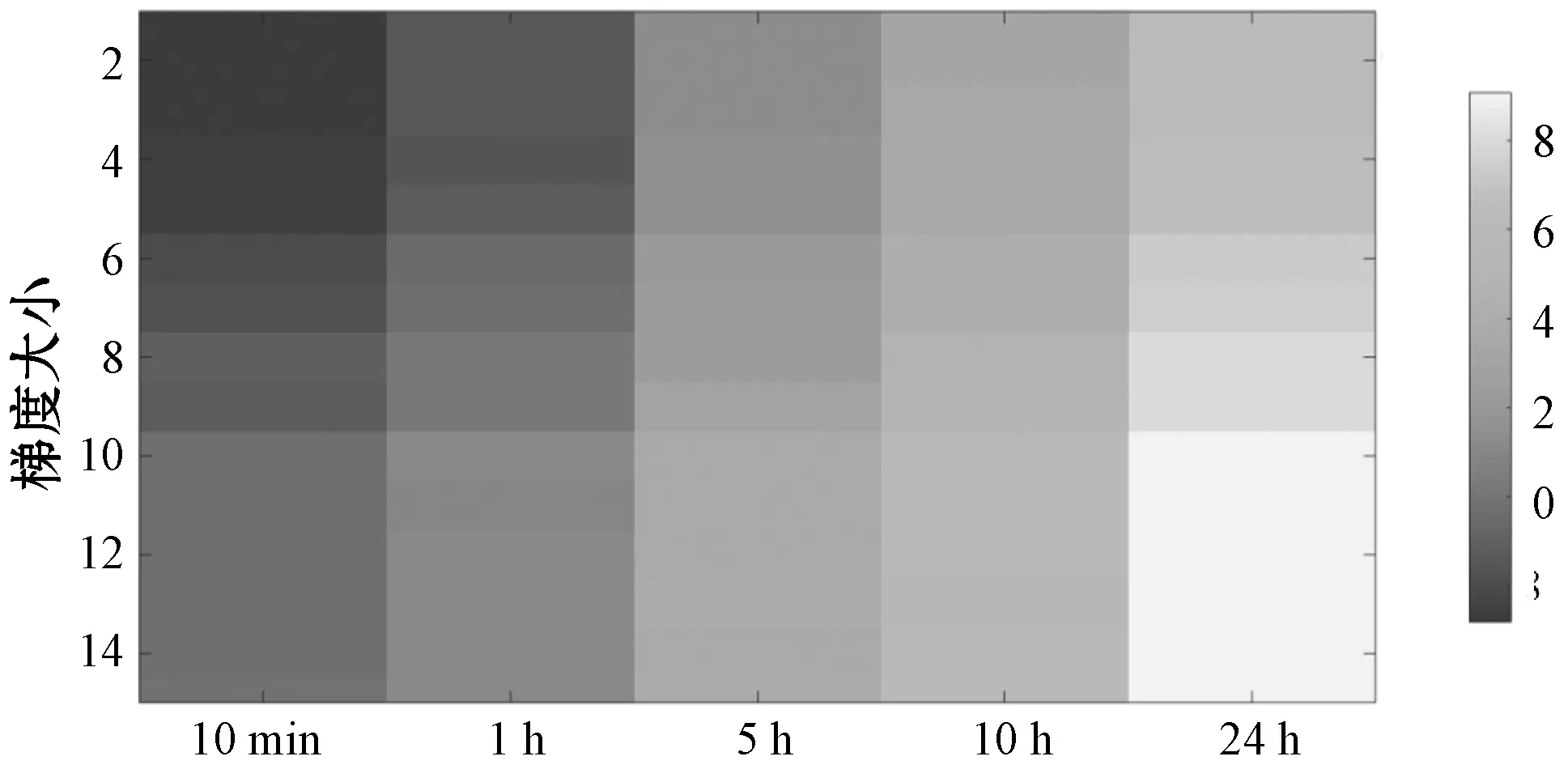
图13 基于不同下降梯度的DH离线训练时间

5 结 语

本文提出一种基于深度学习、粗糙集理论和模糊集理论的风电预测混合模型。为了从风力数据的概率分布中学习特征,设计了一种基于实值输入RBM的无监督概率分布学习模型。将粗糙集理论与深度模型相结合,设计了区间分布学习结构。基于所提出的分布学习模型和模糊II型推理系统,进一步设计了一个具有上下界参数估计的区间深度置信网络。利用所提出的IPDL的特征,将模糊系统应用于底层目标函数的有监督预测。由于IPDL和FT2IS的可微性,该模型利用有监督的期望输出信号,端到端的方式训练模型。本文方法采用粗糙集处理噪声进行特征提取,并且结合模糊推理系统进行预测,仿真结果表明,与其他方法相比,所提出的IPDL模型及其新的学习算法对预测结果有了显著改善,预测结果相当准确。此外,在处理数据不确定性方面,与RBM算法相比,本文算法由于在IPDL中使用了实值输入变量以及区间上下界参数,能够获得变量的深层特征,鲁棒性更好。后续可在具有更高多样性的时间序列特征上进行研究。