基于NSGAⅡ的多目标电子产品CTO订单推荐

韩海峰 叶恒舟 黄凤怡 郝 薇

(桂林理工大学广西嵌入式技术与智能系统重点实验室 广西 桂林 541006)

0 引 言

随着客户对产品需求的不断提高,按订单配置(CTO)成为满足用户需求不确定性和复杂性的关键。CTO模式虽然可为用户在产品选择方面提供多种选择,但这要求企业要能够利用产品结构之间的约束和配置规则等相关算法[1-5]实现产品设计、工艺准备、组织生产,以满足用户的特殊需求。

为快速有效地响应用户订单需求,文献[6]在具有订单配置不确定的CTO系统中,采用启发式算法解决了在多个产品之间分配公共组件的问题。文献[7]通过伸缩的灵活性来适应客户需求的变化,使用按工程订单的生产模式(Engineering To Order,ETO)采用适应性设计和产品平台设计来解决,但ETO模式从产品设计、工艺准备、采购、制造都是按订单操作,不可避免地增加了产品的生产周期和成本。在与CTO模式相似的按订单装配(Assemble To Order,ATO)模式下,文献[8]考虑的是不确定需求和不确定装配能力的ATO模式下的装配决策问题。与本文类似,文献[9]从CTO产品的经济和环境性角度考虑,提出了一种基于多生命周期的多目标产品配置设计方法,并使用NSGAⅡ应用在碳粉盒结构设计的案例中证明该配置方法的有效性,但它仅仅从企业利益和社会利益考虑,忽略了CTO产品是为了满足客户自身需求。文献[10]从用户角度建立了电子产品CTO订单推荐的单目标优化模型,并使用改进的遗传算法求解该模型。

传统的将多目标问题转化为单目标优化问题存在着权值分配主观性强[11]、目标函数复杂[12]、度量单位不一致和搜索效率低等问题。多目标优化算法具有较优的搜索效率和鲁棒性,在诸多领域运用广泛。文献[13] 针对传统优化算法的目标权重人为选择以及常规NSGAⅡ的局部收敛等问题,提出将正态分布交叉(Normal Distribution Crossover,NDX)算子引入到NSGAⅡ中,借助NDX算子加强算法的全局搜索能力,优化出最佳的电网规划方案。文献[14]针对传统动力学模型难以满足精度和稳定性要求,提出一种采用神经网络作为代理模型,建立以马氏距离和鲁棒性为不确定性量化指标的多目标优化模型,并使用NSGAⅡ多目标进化算法求解。文献[15]围绕柔性车间调度问题,针对NSGAⅡ收敛性不足的缺陷,引入免疫平衡原理改进NSGAⅡ的选择策略和精英保留策略,成功避免了局部收敛问题,提高了算法的优化性能。文献[16]在水管的经济性的前提下兼顾可靠性指标优化水管网,同时解决最优解分布不均匀使得算法陷入局部最优问题。

综上所述,虽然NSGAⅡ已经得到诸多应用,也已经提出了诸多改进方法,但在应用于具体某个优化模型时,仍有必要进行针对性的优化。本文围绕电子产品CTO订单,建立以功能定位目标贴近度、功耗和成本三项指标为目标优化模型,将NSGAⅡ应用到电子产品CTO订单推荐多目标优化求解中去,通过用户对Pareto非支配集的权重排序为用户实现电子产品的CTO订单推荐。

1 多目标电子产品CTO订单推荐模型

电子产品CTO订单推荐的目标是根据用户的个性化需求,为其推荐产品的配置清单,即为生产该产品所需要的每个配件推荐合适的品牌与型号。用户的个性化需求有些是局部的或者可以容易转化为局部约束,如内存应大于等于4 GB、屏幕分辨率要不低于2 048×1 080、产品外观为黑色等。这类需求可以通过淘汰特定的配件的可行品牌或型号满足。因而,在构建CTO订单推荐模型时,仅需考虑全局性的个性化需求,如功能定位目标贴近度、成本和功耗等。

设某电子产品的产品配置清单涉及m个配件,si为第i个配件的可选项个数(已经根据个性化需求的相关局部约束进行了筛选),mij(i=1,2,…,m;j=1,2,…,si)为第i个配件的第j个可选项,xij(i=1,2,…,m;j=1,2,…,si)为一个 0-1 决策变量,当为第i个配件选择mij时,xij=1,否则,xij=0。

设t1,t2,…,tu等u个指标被用来描述产品的功能定位目标,用f(tk,mij)度量mij与tk的贴近度。记f(tk,0)=0,可用式(1)确定某个配置清单的功能定位目标贴近度μ,记为f1。

(1)

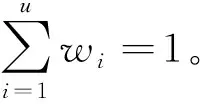
某个配置清单的成本由相应配件的成本及加工成本确定。记cij为mij的价格,c0为加工成本,则某个配置清单对应的成本C可由式(2)计算,记为f2。

(2)

记pij为mij的价格,则某个配置清单对应的功耗P可由式(3)计算,记为f3。

(3)

以最大化功能定位目标贴近度、最小化成本和能耗为优化目标,则多目标电子产品的CTO订单推荐模型(Multi-target Electronic Products CTO Order Recommendation,MEPCTOR)可以描述如下:

目标函数:Maxf1;Minf2; Minf3。

约束条件:

(4)

xij∈{0,1}i=1,2,…,n,j=1,2,…,pi

(5)

式(4)和式(5)表明应为每种配件恰好选择一个选项。

2 MEPCTOR模型求解

MEPCTOR模型是一种多目标优化模型,是NP难的。诸如非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)是求解这类模型的有效方法。本文采用基于NSGAⅡ[17-19]求解MEPCTOR模型,并采用分配权重的非支配集排序策略对求得的非支配最优解进行排序,该算法(CTOR_NSGAⅡ)主要步骤流程如图1所示,主要包括:种群初始化、非支配排序、拥挤度计算、交叉变异和精英保留策略等。

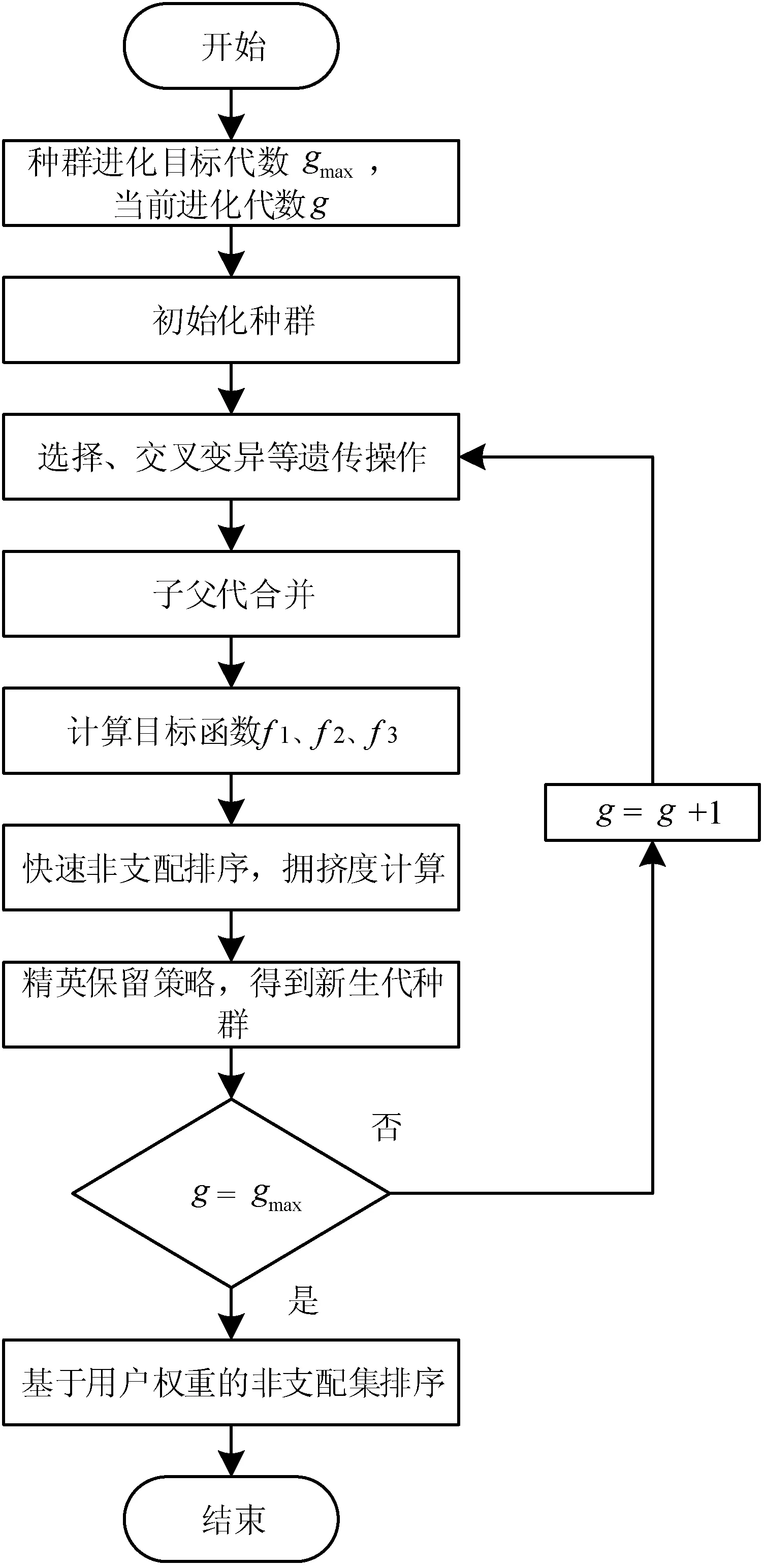
图1 基于NSGAⅡ的电子产品CTO订单推荐流程

2.1 种群初始化

种群染色体采用实数编码方式。一个染色体由十个基因组组成,共二十个实数编码,每两个编码为一个基因组,基因组的编码表示电子产品所选择的对应配件,初始种群的染色体基因组编码随机产生。

2.2 非支配排序

对于每个染色体q设置一个集合sq和一个变量nq,sq为染色体q支配的个体集合,nq记录染色体q被支配的个体数目。快速非支配排序步骤如下:

(1) 初始化种群,设置染色体q对应的sq={},nq=0。

(2) 遍历种群P中的每个染色体q,比较f1、f2、f3函数,找出种群中nq=0的所有个体,并保存在当前集合F0中,记录当前支配等级为0。

(3) 遍历当前F0层的所有染色体,从其支配的染色体集合sq中选择染色体执行nq=nq-1操作,若nq=0,则将个体保存在下一个F1中,记录当前支配等级为1。

(4) 依次执行步骤(2)、步骤(3)操作,直至所有染色体完成分级。

2.3 拥挤度计算

拥挤度是表示种群中个体周围的染色体的密集程度,每条染色体拥挤度是根据周围染色体的距离决定,距离越大表明该染色体所处区域密度越小。因此计算拥挤度是保证种群多样性的一个关键环节。染色体拥挤度的计算如下:

式中:fw(i)表示当前等级下的第i个染色体的第w个目标函数值;fwmax、fwmin分别为当前等级下的第w个目标函数的最大与最小值。当前等级的两端的个体的id=∞。当染色体非支配等级相同的时候,拥挤度大的个体会有更大概率被选择进入下一代,从而保证种群染色体集的多样性。该计算方式可以消除不同量级函数的单位限制,提升染色体拥挤度的计算精度,保证种群多样性的可靠性。

2.4 交叉变异

交叉与变异是种群产生新染色体的主要方式,也是种群进化的重要部分。种群的交叉变异主要采用多点交叉的方式:即从每个基因座编码的起始点(上一个基因座的末尾)到下一个基因座的起始点。每个染色体的基因都有固定的交叉变异概率pc、pm。

以实数编码为例,染色体A的基因编码为[03 11 32 08 13 26],染色体B的编码为[19 25 07 15 02 22],发生交叉互换的位置分别在基因座1、4和6上,那么交叉过后的新染色体A编码为[19 11 32 15 13 22],新染色体B编码为[03 25 07 08 02 26],如图2所示。多点变异类似于多点交叉,若图2中染色体A的基因座1、4、6发生变异,则新染色体A的编码为[**11 32**13**],**为从相对应的基因座编码空间中随机选取的编码。

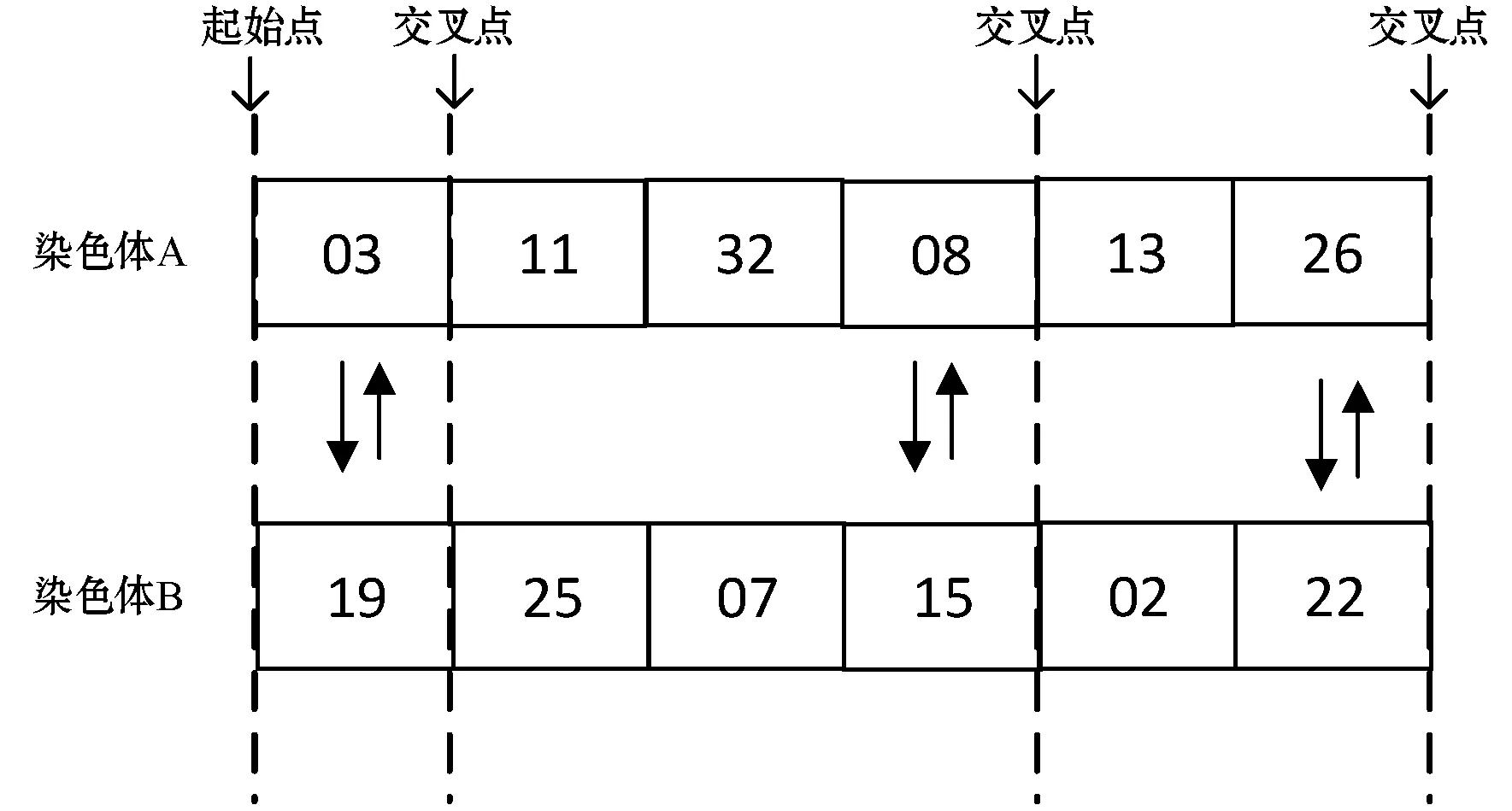
图2 染色体交叉

2.5 精英保留策略

种群Pn和经过遗传操作得到的子种群Qn合并为2N个染色体的解空间。对该空间进行非支配排序,根据非支配等级从低到高依次向新种群Pn+1中添加非支配集,直至新种群Pn+1染色体数量大于等于N。若个体大于N,则从最大的等级中的个体进行拥挤度比较,依次添加个体直至新种群Pn+1个体为N;若个体等于N,则操作结束。

2.6 基于用户权值的非支配集排序

由CTOR_NSGAⅡ得到的Pareto最优前沿点集记录在新种群Pn中,它们的获取与用户偏好无关。接下来可以根据用户的偏好对新种群Pn进行非支配排序,选择非支配等级最低的非支配集。将非支配集中个体的f1、f2、f3目标函数值进行归一化处理,归一化标准按照式(7),根据用户偏好设置目标函数权重,按大小依次排序,得到基于权重的非支配解排序,即为基于用户的电子产品CTO订单推荐。

Norw=α+(1-α)·Testw

(8)

式中:Testw是第w个目标函数的测试函数;Norw为当前第w个目标函数的归一化函数;fwi为当前第w个目标函数的第i个函数值;fwmax、fwmin为当前第w个目标函数在当前数据库中或当前电子产品市场的最大值和最小值;α为可调参数,该值是根据测试函数Testw的值所确定,可消除不同函数在归一化后因数值差距过大而对用户对权重的影响。

整个推荐过程可以分为两大步骤:由CTOR_NSGAⅡ得到Pareto最优前沿点集;根据用户偏好对Pareto最优前沿点集进行排序,择优向用户推荐。前者虽然耗时较多,但与用户偏好无关;后者耗时较小,可以方便用户随时调整自己的偏好。

3 实验及仿真数据分析

3.1 实验环境及参数取值

为验证CTOR_NSGAⅡ对MEPCTOR模型的求解的可行性,本文考虑桌面级PC机为对象,使用网络爬虫技术从公开的网络平台爬取涉及显示器、CPU、GPU、主板、内存、硬盘、电源、键盘、鼠标和耳机等10个配件的共计约348条记录,其中单个配件的记录最小23条、最高52条。实验主要在Intel (R) Core (TM)i7-9750H、2.6 GHz CPU、16 GB RAM、64 bit Windows 10操作系统的PC端进行,算法采用Python3.7编程。CTOR_NSGAⅡ在求解对MEPCTOR问题时具体参数设置如下:初始种群规模为N=20,染色体长度l=10,交叉概率pc=0.50,突变概率pm=0.20,指标权重wi=0.1(i=1,2,…,l),起始目标遗传代数g=40,最大目标遗传代数gmax=200,其中遗传步长step=40。

3.2 仿真结果与分析

为了验证基于MEPCTOR模型的CTOR_NSGAⅡ的有效性,仿真测试结果主要与简单遗传算法(Simple Genetic Algorithm,SGA)以及基于遗传算法改进的ADM_GA[10]对比,该算法根据用户需求将功能定位目标贴近度、电子产品功耗值、电子产品成本值分别赋予权值,该值的归一化处理也按照式(8)计算。

在gmax=100的情况下,选取CTOR_NSGAⅡ所得的Pareto最优前沿点集,并对点集的目标函数f2和f3采用式(7)进行归一化处理,得到Pareto最优前沿点集分布图,如图3所示。

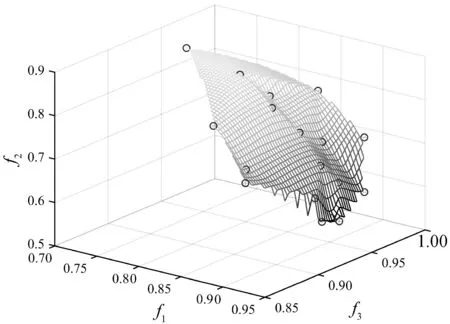
图3 CTOR_NSGAⅡPareto最优前沿面

为了验证算法的可靠性,SGA仿真实验在一次实验中取多个最优解,CTOR_NSGAⅡ则在达到与SGA相同目标遗传代数的情况下,取最低Pareto等级的前几个非支配解进行分析。表1选取gmax=100的情况下,三种算法分别取5个基于用户权值的电子产品CTO订单推荐指数,并计算数学期望与标准差。从表1中不难看出,CTOR_NSGAⅡ在推荐指数上均优于SGA和ADM_GA,均值均优于SGA和ADM_GA,且算法所得推荐指数的标准差低于其他两种算法。

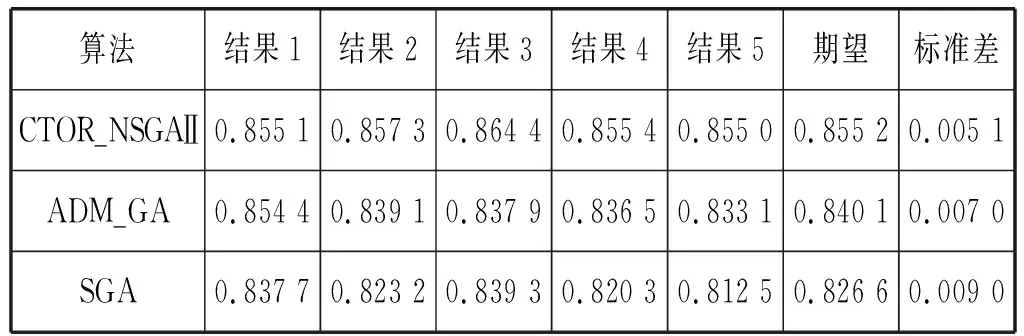
表1 三种算法推荐指数结果对比表

图4给出了三种算法各代电子产品CTO订单推荐指数的数学期望,CTOR_NSGAⅡ的推荐指数期望值最高,CTOR_NSGAⅡ与ADM_GA推荐指数期望值随遗传代数呈缓慢增长趋势,电子产品CTO订单推荐的有效性也随之增强,而SGA缓慢增长后呈逐渐平稳趋势,电子产品CTO订单推荐效果劣于ADM_GA与CTOR_NSGAⅡ。

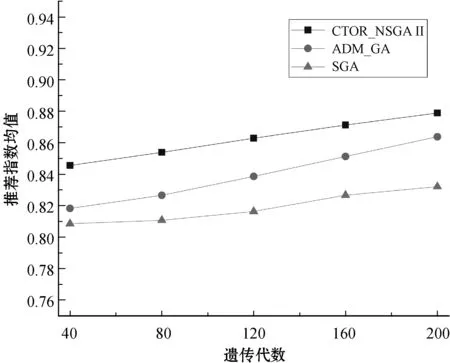
图4 三种算法的电子产品CTO订单推荐指数均值

为了进一步验证两种算法的鲁棒性,测得各代结果的标准差如图5所示。CTOR_NSGAⅡ和ADM_GA相对于SGA标准差更低,鲁棒性相对较强,推荐指数更具平稳性。

图5 三种算法的电子产品CTO订单推荐指数标准差

4 结 语

电子产品CTO订单是按照其产品BOM中的多个模块组件组装而成,因此电子产品的综合指标受组装BOM影响较大。本文针对电子产品CTO订单推荐问题,建立了以功能定位目标贴近度、电子产品功耗和成本值为多目标优化模型,采用CTOR_NSGAⅡ求解该模型,并基于用户权值排序的方式供用户选择。实验证明,该算法较基于权重的SGA和ADM_GA具有较强的鲁棒性和灵活性。