条条大路通罗马

龚宣儒

学习了第七章“平面图形的认识（二）”，我发现平行线、三角形、多边形都可以用来处理角度问题。以苏科版数学教材第40页第9题为例：

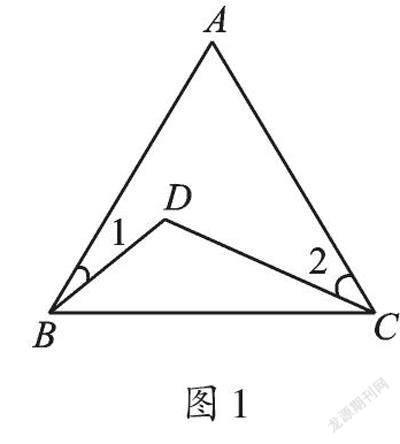
如图1，在△ABC中，∠A=62°，∠1=20°，∠2=35°，求∠BDC的度数。

刚接触这道题时，我发现这里有两个完整的三角形，即△ABC与△BDC，于是我立刻想到用三角形内角和定理来处理。

如图2，在△ABC中，∠A+∠ABC+∠ACB=180°，即∠A+∠1+∠3+∠2+∠4=180°；由已知条件，可求得∠3+∠4=63°；在△BCD中，∠3+∠4+∠BDC=180°，所以∠BDC=117°。

刚放下笔，我不禁想到，平时学霸们都能一题多解，那么对于这道题，我还能想到其他方法吗？俗话说“条条大路通罗马”，于是我再次陷入思考。

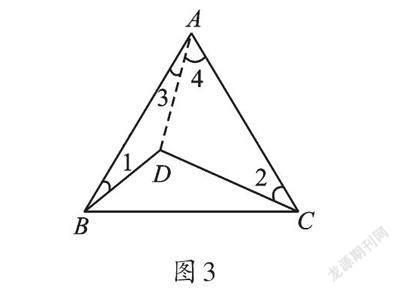
看，这里除了比较直观的两个三角形，不还隐藏着两个吗？如图3，连接AD，设∠3=x°，则∠4=（62-x）°，根据三角形内角和定理，可得∠ADB=（160-x）°，∠ADC=（83+x）°，所以∠BDC=360°-∠ADB-∠ADC=117°。

做到这里，我发现，用三角形内角和定理求∠BDC还有很多方法，比如，还可以延长BD，构造新的三角形。

原来三角形内角和定理这么有用！那利用三角形的好朋友——平行线，能求∠BDC的度数吗？經过尝试，我又收获了惊喜。

如图4，过点D、C分别作AB的平行线DE、CF，可以得到∠3=∠1=20°，∠A+∠ACF=180°，所以∠ACF＝180°-∠A=118°，可得∠DCF=∠ACF-∠2=83°。又因为∠EDC+∠DCF=180°，所以∠EDC＝97°，所以∠BDC=117°。此外，还可以像图5、图6那样构造辅助线哦，这里我就不再赘述啦，相信聪明的你肯定知道如何解答。

思路一旦打开，我的大脑就兴奋不已。我又想到了多边形的内角和，那么本题还可以用多边形内角和来求解吗？

如图7，由于四边形ABEC的内角和是360°，所以∠DBE+∠E+∠DCE=360°-∠A-∠1-∠2=243°。又因为四边形BDCE的内角和是360°，所以∠D=360°-（∠DBE+∠E+∠DCE）=360°-243°=117°。

看来，真的是“条条大路通罗马”啊！随着思考的深入，我真切地感受到，一道题居然可以从这么多角度、知识点切入。我不由得想起一句话，“我们可以由读书搜集知识，但必须利用思考把糠和麦子分开” 。解题方法各有不同，难度也不同，我们只有多思考，多探究，多比较，把学过的知识综合起来，才会对题目有更深刻的理解，才能最终将复杂问题简单化。

教师点评

小作者平时善于多向思考，善于把学过的知识联系起来思考问题。这一题本质上向我们传递了这样一个信息：我们既可以通过三角形、多边形内角和或多边形外角和转化角，又可以通过平行线中的“三线八角”转化角。它们相辅相成，各有优劣。希望在平时的练习过程中，我们能坚持像小作者这样多角度分析问题，收到做一题胜过做十题的效果。

（指导教师：顾向红）