从“平行线”走向“多边形”

许斌

在“平面图形的认识（一）”中，我们认识了线段、角，知道了平面内两条直线的位置关系有相交和平行这两种，还学习了相交情况下的特殊位置关系——垂直。通过“平面图形的认识（二）”，我们将接触平行线的判定及性质；认识平移，探索平移的性质；了解三角形的相关概念，探索三角形的三边关系、内角和及多边形的内角和、外角和等。下面让我们一起走进本章的内容吧！

一、平行线的判定、性质及应用

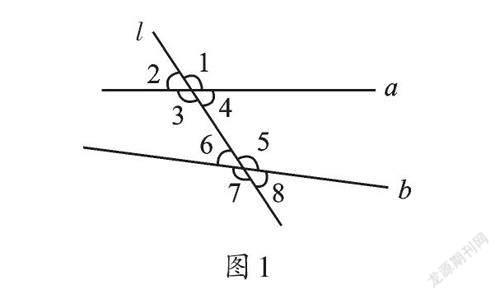
上学期，我们通过两直线相交形成夹角的特殊化，认识了垂直，知道了垂直的定义、判定及性质等。如何判定两直线平行呢？从定义的角度判定不现实。那么，能否类比垂直的研究，从相关角的数量关系来认识呢？我们知道，两条直线平行就意味着两条直线的方向一致，而直线的方向可以通过夹角来刻画。那么，角在哪儿呢？聪明的你一定想到了，画一条直线分别与两直线相交，此时会出现8个角，我们简称这样的图形为“三线八角”，如圖1所示。

像∠1与∠5这样的一对角，称为同位角；∠3与∠5称为内错角；∠4与∠5称为同旁内角。当∠1=∠5或∠3=∠5或∠4+∠5=180°时，我们就可以判断a∥b；反之，当两直线平行时，我们也添上一条截线，此时同位角相等，内错角相等，同旁内角互补，这就是平行线的性质。从平行线的判定和性质我们可以看出：几何图形中，数量关系决定位置关系，位置关系也决定了数量关系。

生活中广泛存在“平移”的现象。在图形平移的过程中，蕴含大量的平行线。通过观察、实验，我们可以发现，平移前后对应点连线、对应线段平行且相等。利用平移的性质，我们可以解决一些实际问题。在此过程中，我们不仅能体会平移的应用价值，还将提高分析问题、解决问题的能力。

二、三角形与多边形

三角形是最简单、最基础的多边形，生活中随处可见。探索和掌握三角形的性质可以帮助我们更好地认识现实世界，发展空间观念。通过用小棒搭三角形的数学实验，我们可以得到三角形的三边关系：三角形任意两边之和大于第三边。在小学我们就知道，三角形的三个内角之和为180°，可如何确定这个事实呢？

对数学的研究，我们不能停留在观察的层面，还需要进行说理。解决这个问题，我们需要思考下面两个问题：（1）180°会让我们想到哪些学过的知识？（2）如何将三角形的三个内角聚集？你有转移等角的经验吗？对，通过添加平行线可以实现将三角形的三个内角聚集到一起，从而将其转化为一个平角或平行线下的同旁内角的图形结构。这样，我们就可以说明任意一个三角形的三个内角和为180°。怎么样？有没有感受到数学说理的强大力量？不论三角形的大小、形状、位置如何，三个内角和总是180°，这是一个不变的值。数学就是这样好玩、奇妙！

在认识三角形的基础上，我们进一步推广研究任意多边形的内角和问题。其实只要想办法将多边形转化为三角形就可以了，数学就是这样一步一步向上生长的，这样我们就得到了n（n≥3）边形的内角和公式：（n-2）·180°。根据多边形的一个外角与其相邻内角的互补关系，我们又可以推出多边形外角和的性质：任意多边形的外角和为360°。这也是一个非常美妙的数学结论，体现了几何问题中“变中不变”的魅力。

三、图形学习的展望

斜拉式大桥为什么采用三角形结构？画一个三角形的角平分线、中线、高时，我们发现，三角形的三条角平分线所在的直线相交于一点，中线和高所在直线也有同样的结论。如何用说理的方式说明其一定正确？特殊的三角形——等腰三角形和直角三角形又会有哪些特殊的性质？两个能完全重合的三角形称为全等三角形，对于这个新的数学概念，我们又将从哪些方面研究？四边形的学习我们又该如何展开？一个个问号萦绕在我们的脑海，一个个问题等待我们一起探究、发现！