中考复习:从“数与式”出发
2023-04-07江海人

领 衔 人:江海人
组稿团队:江苏省南通市“江海初数”工作室
一、知识块解析
实数的相关概念,包括相反数、绝对值、科学记数法、实数的大小比较等;平方根、算术平方根和立方根及相关运算;实数的混合运算也是高频考点,比如绝对值化简、零次幂、平方、立方、负数次幂、开平方、开立方等。
整式的考点主要是代数式的求值,整式化简后代入求值,整式的运算(包括幂的运算性质、合并同类项、乘法公式等),还有因式分解。
二次根式的考点主要涉及二次根式的性质、化简及运算,二次根式的估值等。
分式的考点主要是分式和最简分式的概念,分式的基本性质,分式的约分与通分,分式的加、减、乘、除运算,整数指數幂的概念及运算性质。
二、知识结构图
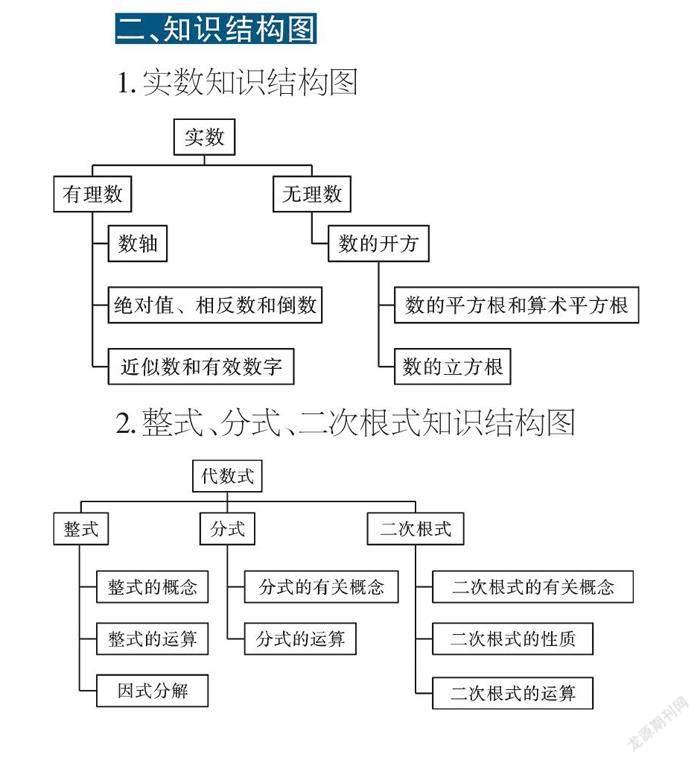
1.实数知识结构图
2.整式、分式、二次根式知识结构图
三、易混点辨析
实数的易混点主要为:对平方根、算术平方根、立方根的概念与性质理解不透。比如,求一个正数的平方根时漏掉一个,而求立方根时又多写了一个;又如,对一个实数归类时只看表面形式,应该化简后再判断;再如,实数混合运算中的“序”也可能出现错误。
整式知识块的易混点也较多。其一,合并同类项与同底数幂的运算要注意辨析;其二,幂的乘方、积的乘方与同底数幂的乘法的不同;其三,整式乘法与因式分解的差别;其四,几个乘法公式之间不能混用。
分式的易混点主要是分式的运算。比如,分式的乘除运算,对于形式上比较繁杂的分式,在约分时容易出错;对于分式的加减运算,主要是在进行异分母分式加减运算时,通常要经历找公分母、通分、加减、化简这4个步骤,由于步骤多、运算量大、综合性强,很容易出错。复习时,我们首先要找准公分母。
要注意辨析二次根式的运算对被开方数(式)的取值范围的限制。一般来说,要“先观察,后计算”“先化为最简二次根式,后计算”“利用乘法公式进行计算”等。值得注意的是,虽然教材以“理解二次根式的性质和运算,并会熟练运用法则进行运算”为重点,突出二次根式的性质和法则的数学本质,而对分母有理化、同类二次根式等概念采取淡化处理,只结合具体例子进行说明,但这并不意味着可以弱化分母有理化。同时要注意,“根号下仅限于数的二次根式的四则运算”的限制是最低要求,复习时要适当训练含有字母的二次根式的化简、四则运算,因为这类二次根式的化简运算不一定会直接考查,有时可能会出现在一些综合题的解题过程中。
四、实际运用
1.已知a[+1a]=[10],求a[-1a]的值。
2.已知x=2-[3],求代数式(7+[43])x2
+(2+[3])x+[3]的值。
3.根据下列条件求代数式[-b+b2-4ac2a]的值。
(1)a=1,b=10,c=-15;
(2)a=2,b=-8,c=5。
复习建议:第1题复习之后,可思考“当a>0时,分析代数式a[+1a]的最小值”;第2题复习后,可以想一想如何化简[7+43];第3题复习后,可结合一元二次方程的求根公式来理解这道题的设计意图。
(作者单位:江苏省海安市城南实验中学)
