面向保护需求的虎丘塔虚拟修复
2023-04-06熊雅行傅静文
熊雅行 傅静文
(1. 江西理工大学 土木与测绘工程学院, 江西 赣州 341099)(2. 吉安职业技术学院 现代农林工程学院, 江西 吉安 343006)
0 引言
中国古建筑依山傍水,形式多样,风格用途各不相同,它们除了传统意义上作为人们居住生活地外,还具有极高的审美价值和研究意义[1]。然而,在国家高速发展、快速城市化的现在,大多古建筑都有不同程度的损坏。在历经岁月的保存中,古建筑不断遭受风化、侵蚀和破坏[2]。所以,对古建筑的修复、维护和保存迫在眉睫。
在传统的古建筑修复过程中,通常是人工使用皮尺、卷尺结合水准仪等传统测量仪器对建筑物进行测量,导致过度依赖人工,不仅耗时很多、效率低下而且精度不高。随着计算机的发展、三维激光扫描技术[3]的成熟、三维建模[4]和虚拟现实技术[5]的发展。人们越来越将传统的古建筑修复工作转移到计算机辅助的古建筑虚拟修复上来。虚拟修复技术是利用虚拟现实技术结合物体形状、颜色等信息以及保留下来的数据、图纸和历史文献在电脑上对其进行修复[6]。
Biermann等人[7]提出了一种基于多分辨率细分曲面的算法,用交互式的剪切和粘贴方法以将不同的元素组合到一起。Lu等人[8]应用了一种基于刚性表面匹配的方法,并利用同一尖顶中的四个面具有相似性的特征,在柬埔寨巴戎寺的文物修复和保护中对受损佛面进行了虚拟修复。侯妙乐等人[9]提出了一种基于多尺度空间几何特征的虚拟修复方法,根据全局信息和局部特征确定破损部位的几何形状和具体信息。利用虚拟现实技术和计算机技术等对千手观音进行修复及数字化保存。李春龙等人[10]提出了一种依据破损文物的几何拓扑信息得到文物的对称轴和母线信息,在对破损文物进行虚拟修复的方法。杨承磊等人[11]利用二次曲面拟合方法计算物体的旋转轴,再利用旋转轴还原常见的旋转体。本文将结合上述研究方法的优势,利用虚拟修复技术对古建筑物进行修复。
1 研究方法
本文采用虚拟修复为研究方法,它将点云数据、历史信息和建筑实体信息相结合并利用计算机技术和三维建模技术对目标物体进行虚拟修复。相对于传统修复方法,它具以下优势:提供精确、科学的古建筑数据;避免二次伤害;具有多次修复机会;信息数字化;可以进行数字化展示。
建筑实体的破损部分采集不到点云数据,一般情况下,采取手动几何编辑和曲面拟合等方法对其进行修补。在本文中使用邻域相似修复原则对古建筑进行修复,在古建筑的其他区域搜索与建筑物缺损部分匹配程度最高的几何块,作为古建筑虚拟修复的数据,对古建筑进行虚拟修复。
1.1 旋转中心
点云数据是空间中散乱的数据,通常都是大量数据一起存在。除了可以表示被扫描实体的外轮廓信息的,还有大量的冗余信息。采用点云切片技术可以在保留点云有效信息的同时减少冗余信息。点云切片的原理为采用一组平行的平面与海量的点云数据相交,将平面两侧的点云投影到平面上获取相关的点云数据[12]。由于点云数据是有密度的,所以在切片时要选取合适的切片厚度。如果切片厚度值太小就可能会丢失一些轮廓信息,但是太大会得到大量的点云数据,得到一些冗余信息。得到点云切片的数据后,再利用轮廓点的坐标数据求该切片的几何中心。得到每个切片的中心坐标后,将这些点连起来就可以获得实体的几何中心轴线。
1.2 点云修复
对于点云缺失的部位,目前已经研究出多种方法来对其进行修复。例如,曲面拟合[13]、交互式剪切[14]和粘贴以及结合多种数据进行修复的方法等。在本文的实验中,根据修复实体的几何对称性来进行修复。首先要根据实体的全局信息选取与破损位置匹配程度最高的几何块。再利用几何块的点云数据旋转到点云缺失部位对破损部位进行虚拟修复。
选取合适的几何块,将该几何块的点云数据单独导出来。计算几何块与破损位置之间的角度θ,再将导出的点云数据旋转θ获取新的点云数据坐标。三维坐标转换公式如下:
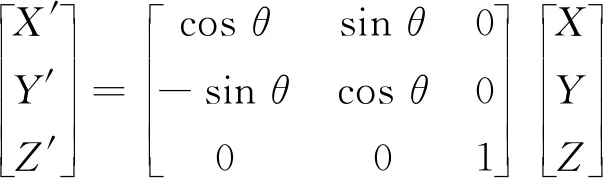
(1)
其中,X、Y、Z分别表示已知点云数据的纵坐标、横坐标及垂直坐标;X’、Y’、Z’分别表示新的点云数据的纵坐标、横坐标及垂直坐标。
扫描实体的点云数据获取时,每个测站都是独立坐标系。完成点云数据配准后,所有测站的点云数据坐标都是第一站的测站坐标。而将点云数据进行旋转时要根据实体的旋转中心进行旋转。所以我们要先将测站坐标系的原点设置成旋转中心,再将旋转后的点云数据导入到原始的点云数据中,就完成了对点云破损部位的虚拟修复。
2 实验结果
2.1 数据采集
虎丘塔不同于普通房屋建筑,建筑结构四四方方。虎丘塔具有七层,每层都有八个面[15]。除了要考虑虎丘塔八个面的特殊建筑结构,还要考虑虎丘塔的围墙在数据采集时对塔身的遮挡。在对虎丘塔进行数据采集时使用的是法如(Faro)的三维激光扫描仪,分为8站对虎丘塔进行数据采集。在具体野外扫描工作时,应先按照选定好的测站布设点依次进行测量。先在指定位置假设仪器,设置好扫描参数,进行点云采集和相片获取。
2.2 点云拼接
使用Faro的配套数据处理软件法如场景(Faro Scene)对采集到的数据进行处理。导入相邻两站的点云数据,打开这两站的平面视图。根据平面图中查看共同扫描到的区域,再选取合适的平面进行拼接。
点云数据配准精度是具有传播性的,在进行点云数据配准时使用到的测站越多,点云配准精度就会越低。本文的实验中,将点云拼接的精度控制在毫米级。具体的点云数据配准精度如表1所示。
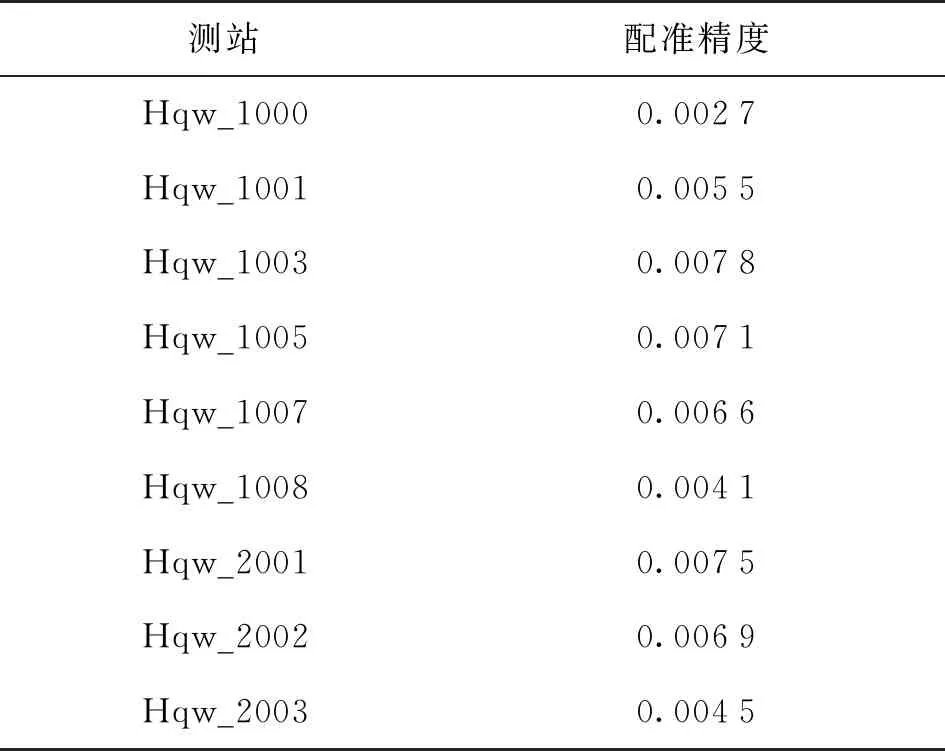
表1 点云配准精度 单位:m
2.3 点云去噪
将多视角的点云数据拼接到同一视角下时,获得了完整的虎丘塔的点云数据。在扫描过程中,除了扫描到建筑主体外,不可避免地会扫描到建筑周边的环境。例如,树木、围墙和周边建筑。在扫描虎丘塔时,由于塔周边的树木茂盛,所以扫描到了较多的树叶。在虎丘塔周围还有虎丘塔的外围围墙、石凳等实体。在后续的数据处理中,这些噪点都会带来很多问题,所以在软件中将其删除。
2.4 虚拟修复
2.4.1 旋转中心提取
将导出来的数据导入到杰魔逆向校核软件(Geomagic Qualify)当中,在逆向校核(Qualify)中对点云进行切片。因为切片的目的是提取多边形的中心点,进而提取出虎丘塔的中心轴线。本次实验中,使用Geomagic Qualify对虎丘塔的点云数据一共进行了8次Z向点云切片,切片厚度为0.05 m如图1所示。
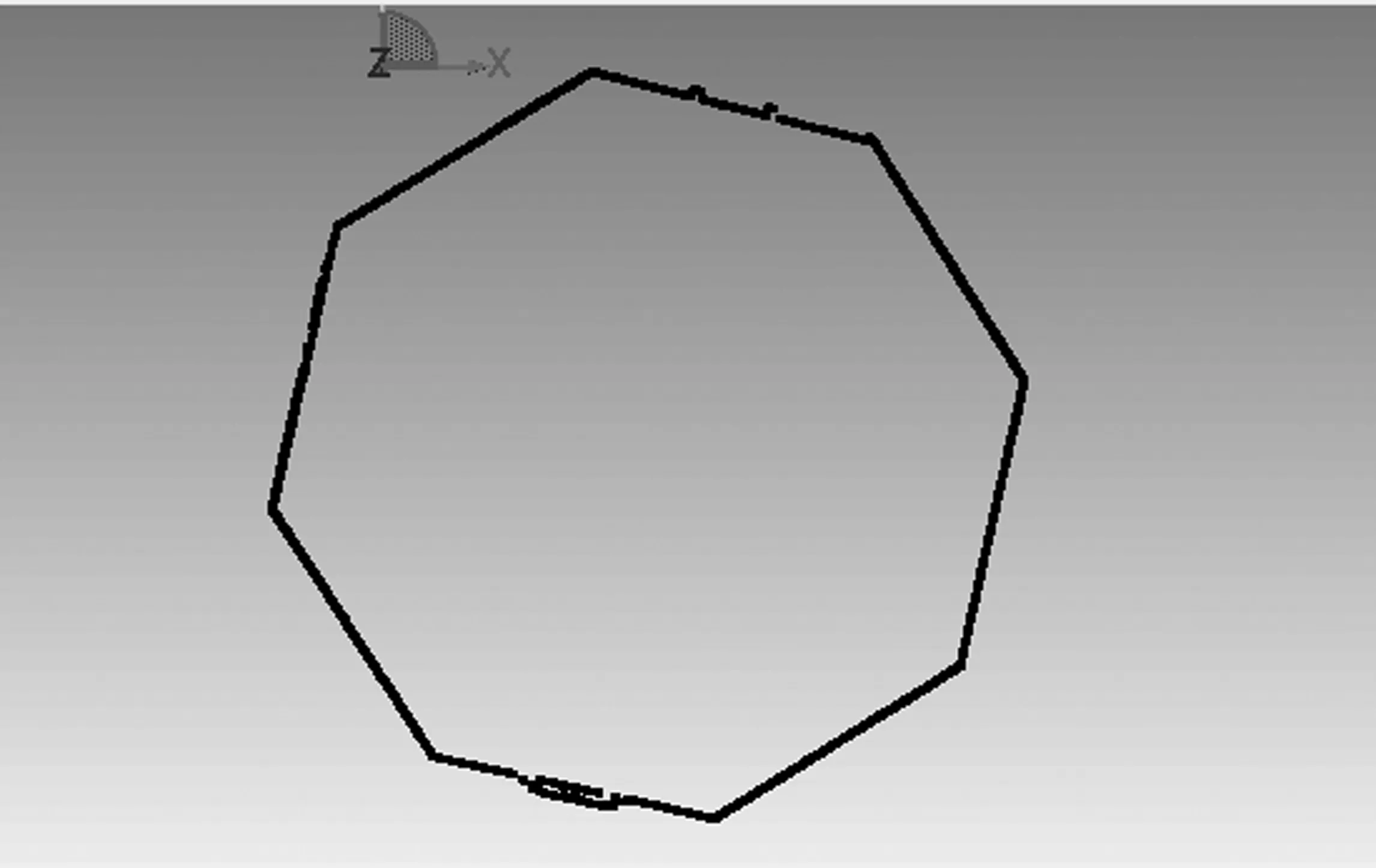
图1 点云切片
导出每个切片的顶点坐标数据,在进行该切片中心的求取。得到中心点的坐标后,在对其进行直线拟合获得虎丘塔几何中心的方程式。由于旋转时,Z轴不发生变化,所以直接将旋转中心点的Z轴坐标设置为0,只求取旋转中心的X轴和Y轴坐标。点云切片的中点坐标如表2所示。旋转中心的坐标为(8.532 4,-12.138 4,0)。
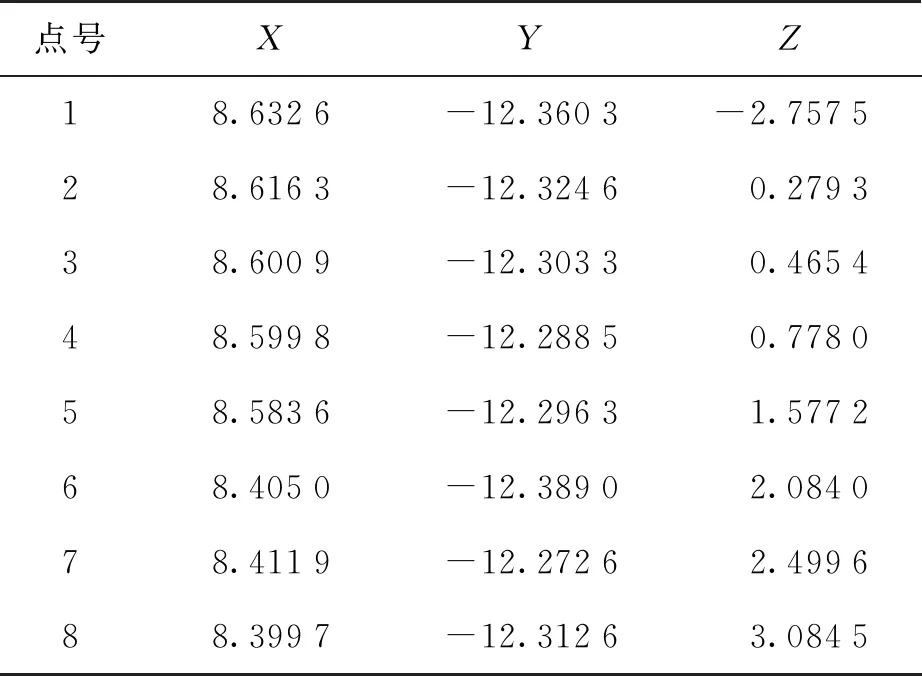
表2 点云切片中点坐标 单位:m
2.4.2点云修复
在对点云进行旋转之前,首先要将旋转中心设置为坐标原点。在Geomagic Qualify中,先将点云的坐标数据导出。将导出的点云数据减去旋转中心的坐标就实现了将旋转中心设置为坐标原点这一目的。
坐标系的转换工作结束后,要选择合适的几何块作为点云修复的基准。导出点云的坐标数据,根据坐标转换公式计算旋转后点云的坐标。再将该点云导入到原始数据中,如图2、图3所示。

图2 点云缺失位置

图3 修补后三维视图
2.5 精度分析
以虎丘塔一个完整的面为例,在该几何块上人工去除一部分点云,在对其进行修复。利杰魔逆向软件(Geomagic Studio)对修复后的点云数据进行三维建模,在Geomagic Qualify中将三维模型与原始点云数据进行三维对比及二维对比,分析修复后模型的精度。
2.5.1曲面模型三维比较
在Geomagic Qualify中导入三维模型和点云数据,先进行最佳拟合。将两者拟合到一起,再进行三维比较。结果显示最大偏差为0.263 0 m,最小偏差为-0.246 0 m,平均偏差为-0.002 5~0.002 5 m。标准偏差为0.011 6 m。模型的整体误差数值如表3所示。
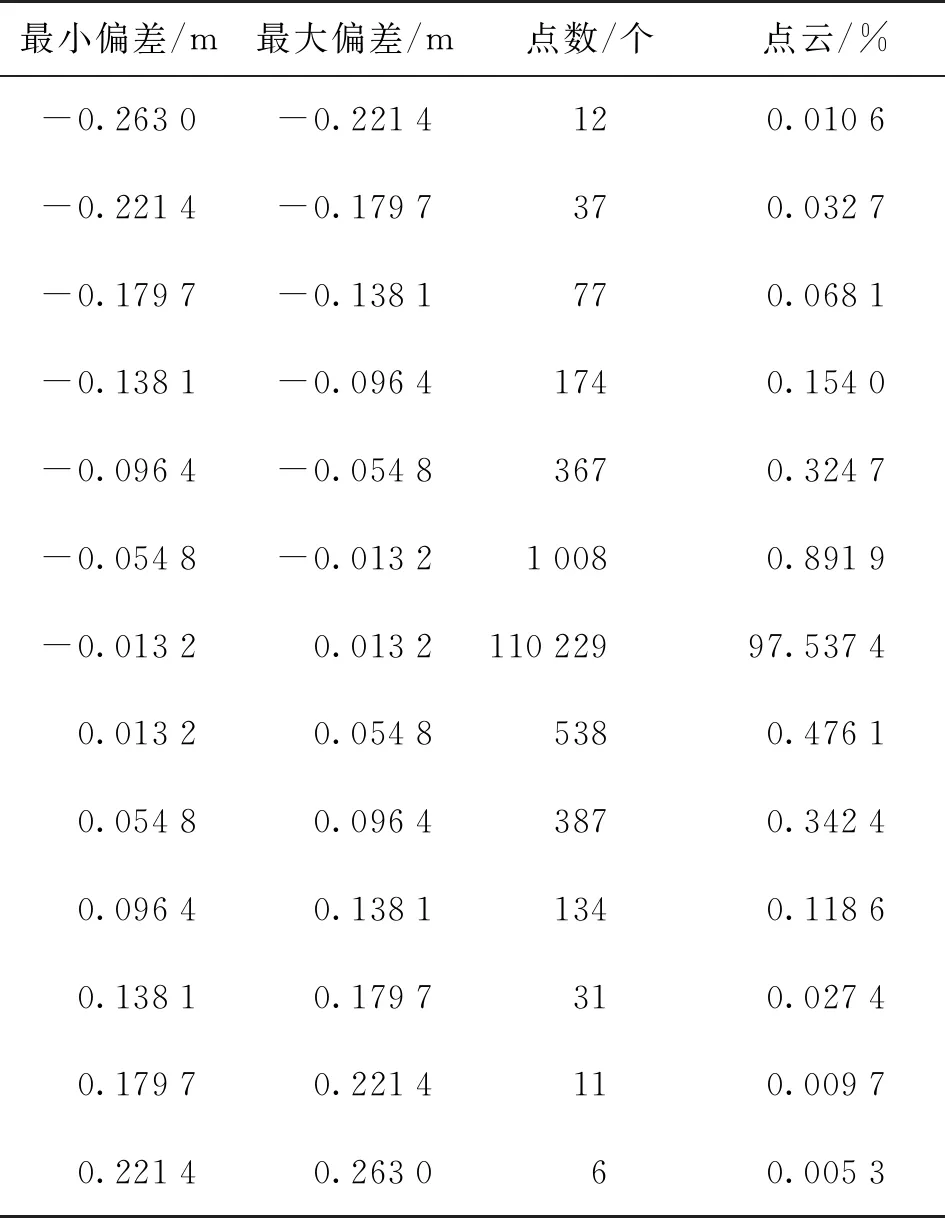
表3 整体误差分析
从表中可以看出,误差在-0.013 2~0.013 2 m的点云为97.53%。
2.5.2模型的二维比较
在XY平面Z=0.408 2 m处对其进行截取进行二维分析,结果表明在这个截面上,最大偏差为0.006 2 m,最小偏差为-0.01 5 m,平均偏差为-0.001 0~0.001 0 m。标准偏差为0.001 0 m。二维平面的误差如表4所示。
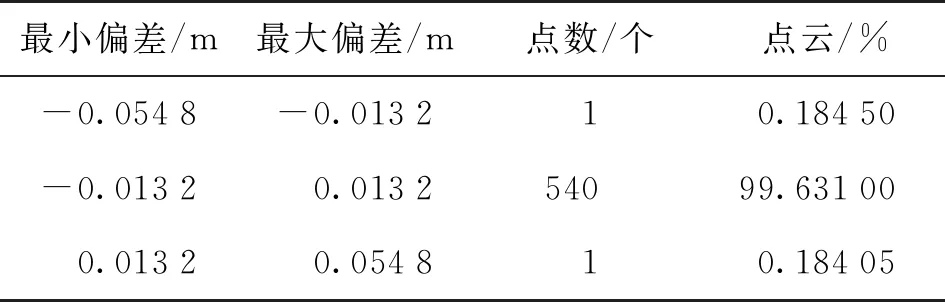
表4 模型XY平面误差分析
在该截面上一共有542个点。从表中可以看出,偏差在-0.013 2~0.013 2 m的点云为99.63%。
3 结束语
本文以虎丘塔古建筑的虚拟修复为研究目标,在通过三维激光扫描仪采集得到虎丘塔的点云数据后,接着对数据进行预处理、配准和去噪,最后通过切片和最小二乘拟合方法将选中的几何块绕旋转中心旋转一定角度进行虚拟修复。实验结果表明,本文方法对虎丘塔修复效果较好,精度较高,对其他古建筑物的修复有借鉴意义。本文主要利用虎丘塔的对称性对其点云缺失部分进行修复,只利用了已有的点云数据进行研究,下一步研究方向可以考虑融合多源数据来对其进行修复。
