煤的孔隙结构分形特征研究

位 乐，王登科，陈 旭，沈建廷，宫玖朋，闫 晓

（1.中煤科工集团重庆研究院有限公司，重庆 400037；2.河南理工大学 安全科学与工程学院，河南 焦作 454000；3.大方绿塘煤矿有限责任公司，贵州 毕节 551604）

煤是一种典型的多孔介质地质材料，其中所富含的孔隙是煤层瓦斯储存的主要场所，直接影响瓦斯的吸附解吸特征，对煤孔隙结构开展研究对揭示煤吸附机理具有重要意义。煤孔隙网络错综复杂，用传统的方法很难对其进行准确度量，分形几何理论为定量表征煤孔隙结构特征提供了可行途径[1-2]。众多学者的研究表明：采用分形理论对煤岩孔隙结构进行研究是简单有效的[3-4]。Kewen 等[5]研究了岩石的节理非均质情况，发现分形维数可以表征节理的复杂程度。Meng 等[6]利用分形理论研究砂岩孔隙结构时，提出了同时计算体积与面积分形维数的计算方法。李志清等[7]基于分形理论采用压汞实验、氮气吸附实验及核磁共振实验数据对页岩孔隙结构进行了定量表征，揭示了孔隙结构与分形维数之间的关系。杨宇等[8]对不同煤阶的煤炭样品进行了分形维研究，发现不同煤阶的分形维不同。Wang 等[9-12]的研究结果发现，煤内部的孔裂隙结构具有明显的自相似性，并建立了基于分形表征的孔隙瓦斯气体传输方程和分形渗流模型，较好地描述了煤层瓦斯的流动机制和流动规律。

目前的研究大多基于一种实验手段对煤孔隙结构进行分析，采用单一的实验手段很难对煤层孔隙结构进行准确的描述和分析。并且学者们对煤岩孔隙结构分形的研究手段比较单一，综合研究薄弱，不能充分表达孔隙结构的分形特征。煤具有复杂的孔隙结构特征，煤的孔隙结构分形特征也尚未进行定量表述。

1 煤的孔隙结构实验研究

本文采用Χoдoт 的十进制分类方法[13]按照微孔（＜10 nm）、小孔（10～100 nm）、中孔（100～1 000 nm）、大孔（1 000～100 000 nm）来分析煤的内部孔隙结构特征。实验所用6 个煤样取自于安阳主焦煤矿（焦煤、编号ZJ）、汾西中兴煤矿（焦煤、编号ZX）和沁和永安煤矿（无烟煤、编号YA）。至采煤工作面选取块状较为规整的原煤，用保鲜膜包裹新鲜煤样，编号带回实验室。在实验室将原煤破碎，筛选出60～80 目的粉煤，粒径为0.20～0.25 mm，制备成煤样。煤样制备完成后将煤样放入恒温干燥箱中烘干，以去除煤样中的水分对后续实验的影响。

利用制作好的煤样分别开展低温液氮吸附和压汞实验。根据测试结果可得到孔径大于2 nm 的孔隙结构信息。3 个矿煤样各孔径阶段比表面积分布见表1。

表1 煤样孔比表面积分布

由表1 可知，大孔范围内，3 个煤样累计孔比表面积均很小，差距不大；中孔范围内，3 个煤样累计比表面积开始明显增加；小于100 nm 的孔隙，累计比表面积快速的增加，曲线直线上升。总孔比表面积大小的排序为ZJ 煤样大于YA 煤样大于ZX 煤样。ZJ 煤样和YA 煤样比表面积贡献比，微孔大于小孔大于中孔大于大孔，ZX 煤样比表面积贡献比小孔大于微孔大于中孔大于大孔。

2 煤孔隙结构分形特征

2.1 基于低温液氮吸附实验的孔隙结构分形描述

计算煤吸附孔分形维数时，FHH 模型[14]应用较为广泛，其表达式为

式中：V 为平衡压力p 下的气体吸附量，cm3/g；K 为拟合直线的斜率；p0为气体的饱和蒸汽压，0.11 117 MPa；p 为气体吸附平衡时的压力，MPa；C 为常数。

实验数据拟合结果如图1 和表2 所示，从表2 中可以得到ZJ、ZX 和YA 煤样的分形维数分别为2.409 3、2.427 7、2.442 7，拟合曲线的相关系数均在0.95 以上，这说明煤孔隙结构具有非常典型的分形特征。

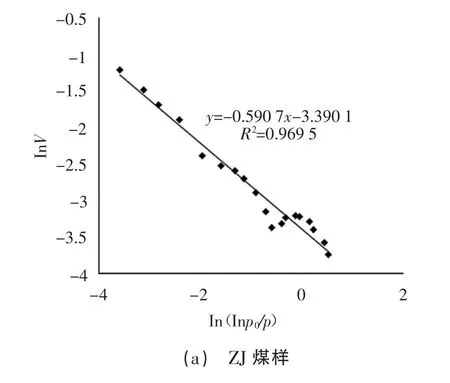
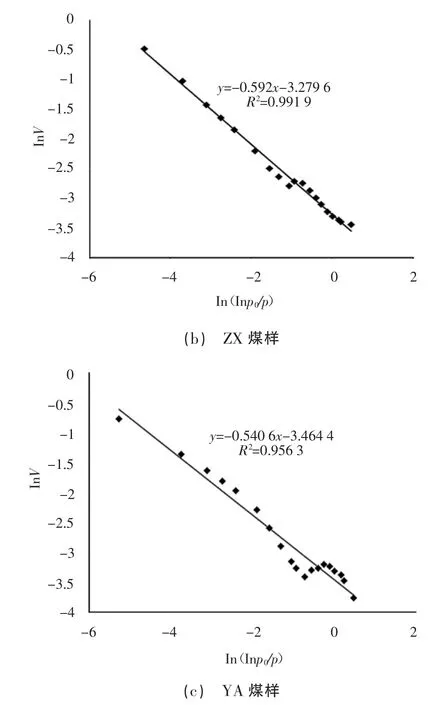
图1 低温液氮吸附实验数据拟合结果

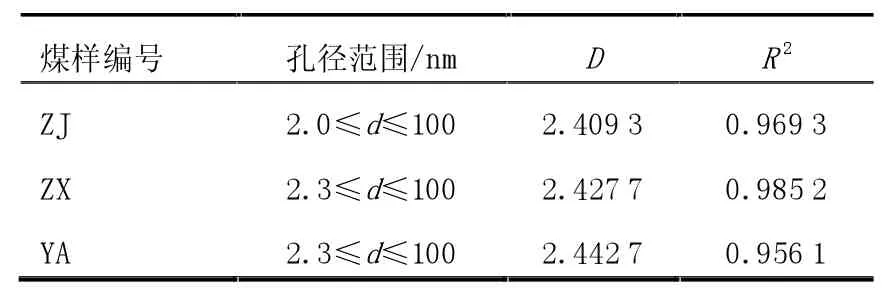
表2 煤的分形维数计算结果（低温液氮吸附实验）

2.2 基于压汞实验的孔隙结构分形描述

多孔介质的孔隙体积与分形维数满足方程

式中：Vp为孔隙体积，cm3/g；D 为煤体分形维数；p 为进汞压力，psia。

则煤孔隙结构的分形维数计算公式为

式中：K 是线性拟合的斜率。

由压汞实验数据作ln（dVp/dp）-lnp 双对数曲线图，拟合结果如图2 所示，计算结果见表3。从图2 中可以看出，ln（dVp/dp）-lnp 对数曲线图分为孔径d＞100 nm 与d＜100 nm 两部分，煤中孔径d＞100 nm 的孔分形维数在2.3～2.6，具有分形几何意义，孔径d＜100 nm 时的孔求得的分形维数均大于3.7，从经典几何观点来说，D＞3 是不合理的。这说明当p＜10 MPa（d＞100 nm）时，压汞实验法测量出的孔隙才具有典型的分形特征，这也与压汞法的测试精度对应。

表3 煤的分形维数计算结果（压汞实验）

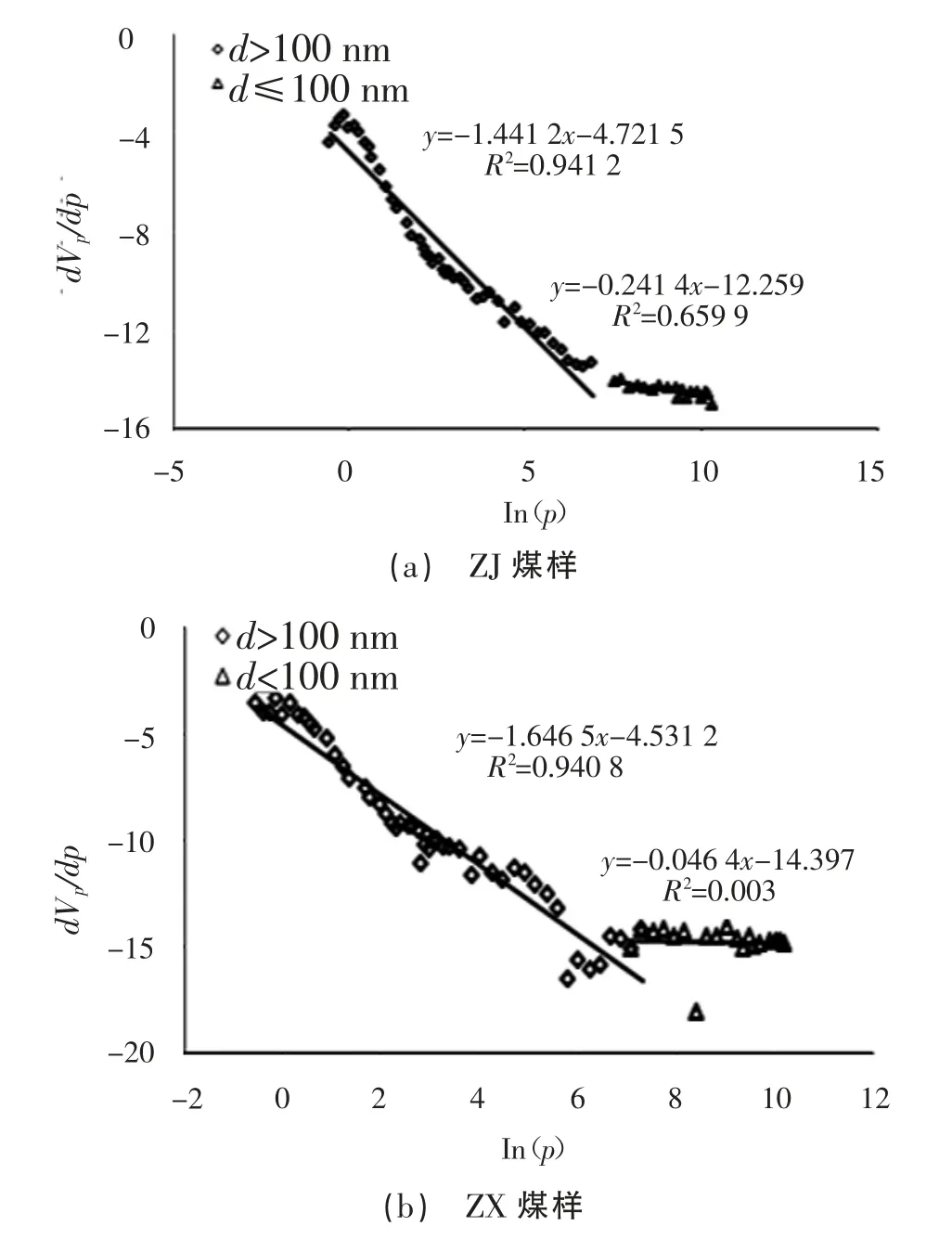
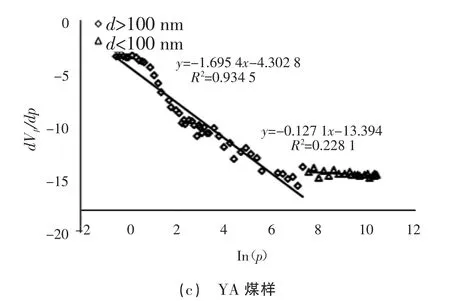
图2 压汞实验数据拟合结果

2.3 煤的综合分形维数

煤内孔隙结构的尺度不一，其对应的分形维数也不尽相同，若按照各个孔径段的比表面积进行加权平均，便可得到其综合分形维数DZ，计算公式为[15]

式中：DZ为煤的综合分形维数；Di为第i 个孔径分布段分形维数；bi为第i 个孔径分布段比表面积比；i 为第i孔径分布段，为正整数；n 为孔径分布段的个数，为正整数。

结合本文前面的计算结果，根据式（4）可得到煤样孔隙的综合分形维数，具体结果见表4。

从表4 中可以得出在孔径大于2 nm 时，ZJ 煤样的综合分形维数大于YA 煤样的综合分形维数大于ZX 煤样的综合分形维数。同时从前面表1 可以得到，在孔径大于2 nm 时，ZJ 煤样总孔比表面积大于YA 煤样总孔比表面积大于ZX 煤样总孔比表面积。因此可知，当孔径大于2 nm 时，煤样内部总孔比较面积随孔隙综合分形维数的增加而增加，两者之间呈正相关性。

表4 煤样综合分形维数统计表

3 结论

本文借助实验测试和理论分析，对煤的孔隙结构的分形特征进行了测试研究，实验测试结果表明，煤中的孔隙结构具有典型的分形特征。通过定义描述孔隙结构整体复杂程度的综合分形维数，发现在孔径大于2nm 时，煤的总孔比表面积随煤的孔隙综合分形维数的增大而增大，煤的总孔比表面积与煤的综合分形维数正相关。