新型四足并联军用机器人步态控制算法及仿真

李姗姗 , 王洪波 , 陈建宇 , 张兴超 , 田俊杰 , 牛建业

(1. 燕山大学 河北省并联机器人与机电系统实验室，河北 秦皇岛 066004; 2. 燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004; 3. 复旦大学 工程与应用技术研究院，上海 200433)

0 引言

军用机器人是用于军事战场的特种机器人，在21 世纪的科技化战场上，军用机器人有着非常广泛的应用场景，小到物资运输大到实战进攻勘探都能看到它们的身影。军用机器人的出现和应用，改变了传统军队的作战方式，促进了现代军事防御的发展。由于军事战场的环境一般都比较恶劣，涉及山地斜坡类的崎岖不平路面，这就对机器人的移动控制提出了更高的要求。

四足机器人移动控制系统为一个非线性控制系统，拥有传感器的多输入到电机的多输出结构，此系统能通过不连续且复杂的动力学计算完成机器人不同工作模式与外界环境的实时切换[1]，实现机器人的快速响应。

目前常用的控制方法有3 种，第1 种为根据零力矩点的多用于控制双足机器人的动态稳定步态[2]算法，其缺点是会造成机器人运行的不稳定性和运动速度缓慢；第2 种是基于有节奏运动生物的中央模式(CPG)的模仿控制方法，即控制机器人的关节是通过多个相互耦合的非线性振荡器输出信号来实现的，其优点是机器人能具有良好的运行稳定性和越障能力[3-5]；最后一种是由Raibert 提出的虚拟模型控制框架方法，即机器人足端运动轨迹的控制是通过直接输入机器人规划好的运动状态(方向、姿态、速度)进行这些物理直觉来实现的，是一种用来描述交互作用力解耦的控制方法[6-9]，此方法在控制过程中能很大程度地简化对计算动力学模型的需求，同时也很大程度地提高了机器人硬件上的响应速度。其次，机器人的各种运动状态参数此方法都可稳定快速地直接进行调整，即使受到外界冲击和干扰时机体也可以快速恢复稳定。

本文针对四足机器人步态提出一种新型控制算法，由CPG 生成机器人行走时的基础步态，完成输入输出之间的非线性振荡器模型搭建，在对虚拟模型进行融合的基础上计算出用于调整机器人姿态的力矩，并借助静力学平衡映射为能够对机器人行走进行控制的关节输出。此方法在简化控制网络的同时还能保证机器人在行走过程中拥有较强的灵活性和抗干扰能力。

1 四足并联军用机器人整机构型介绍

机器人整机机构如图1 所示，机体上安装有 4 条独立且对称的机械腿，将为机器人运动供电的储蓄电池、驱动器和腿部电机安装在机体上，此外还可装载需要运送的货物。

机器人机械腿用3-UPS 机构作为单腿基础结构，在行走过程中机器人的机械腿此时具有6 个自由度，其机构如图2 所示，主要由上基座、支撑和足底组成，结构比较紧凑，可在腿部关节处安装驱动电机和减速器，同时单腿机构也能具有更强的负载能力。机器人主体通过连接板与单腿机构相连，由伺服电机驱动的电动滑台也与连接板相连，且呈120°按圆周均匀分布，借助弹性联轴器丝杠的一端与伺服电机相连，另一端又与滑台相连，伺服电机带动丝杠旋转，从而实现了对滑台的移动控制。单腿机构中的滑台即为3-UPS 机构中的3 个P 副，可实现机器人单腿机构运动参数和机器人四足间距的调整，使机器人在复杂路况下的越障能力和适应能力都得到了很大提高。

图2 单腿机构Fig. 2 One leg mechanism

在机构零件图3 中，机器人的腿部机构由3 个直线驱动副支撑，一端与U 副次轴连接，另一端通过鱼眼轴承和轴承支架安装在足底上。基座部分滑台下端连接主轴支架，与伺服电机固连的型号为NRV030 蜗轮蜗杆减速器与主轴支架相连。U 副主轴一端与减速器相连接，另一端与支架相连，U 副主轴上安装有套筒，图中的U 副次轴由套筒和螺栓构成，其中驱动轴为U 副主轴。因此机器人单腿3-UPS 机构中6 个自由度的驱动动力源是由单腿机构中3 个直线驱动副和3 个驱动U 副主轴的电机来提供的。

图3 机器人单腿的结构图Fig. 3 Diagram of a single leg of the robot

2 四足移动机器人的虚拟步态控制

2.1 基于Kuramoto 模型的虚拟控制模式

针对这一复杂的四足移动机器人控制问题，本文中机器人的腿部末端采用延迟同步模型当作发生器，这样在运动过程中机器人的各腿部机构能保证相互耦合，而便于控制的Kuramoto 模型属于同步的振荡器模型。在此基础上，其能够把一个协同系统从无序复杂状态转化成同步状态的过程模拟出来。本文机器人的关节角度也以相互耦合的4 个Kuramoto 模型当作生成器，并把关节角映射成带有滞后同步的步态时序。

当采用全耦合的方式让单一振子与其他振子相互作用时，用wm表示第m个振子的自然频率，其动力学模型表示为

式中：θm为关节运动的相位，θm随振子每循环一个周期就变化2π；k为振子间相互耦合强度；N为振荡器的数量；θ˙m为振子的频率。当k= 0时，表明各振荡器间互相独立，这时各振子用θ˙m=wm表示其自身的动力学模型，并且每个振子互不影响。

以w为自然频率的独立非线性振荡器，要使其每个振子相互影响，则其耦合系数不能为0。调查结果表明当w满足柯西分布时，N趋于无穷，耦合强度会趋于一个临界值，当其高于此临界值时系统的全部频率均会收敛一致，此时系统变为同步 振动[10]。用一个圆对系统中所有的振子进行描述，且求和平均后，则系统同步的程度即为其值在复平面内质心处矢量的模，用式(2)表示为

式中：i 为虚数单位。式(2)也称复序参量，简称序参量。这里矢量的方向用负指数定义，序参量的取值范围为0 到1，且其值的大小与系统的同步程度有关，值越大则系统的同步程度也越高。即当系统的振子越分散、耦合系数越低时，序参量的值越接近0；当系统的振子耦合系数越高时，序参量的值越接近1，此时序参数较高，系统处于部分同步状态，但仍不能到达单位圆上[11-13]；当系统的序参量为1 时，此时系统处于完全同步的理想状态。由以上分析知系统振子从相互独立到部分相关再到完全同步的状态，是系统中各个相互作用的振子克服了固有频率的结果。

设x为随机变量，将欧拉公式sinx= (eix- e-ix)/(2i)和式(2)代入式(1)，可以得到：

式中：R为复序参量的模；ψ为任意相位。

本文中的机器人在运动时4 条腿都拥有相同的运动轨迹，只是各条腿之间有个固定的相位差存在，因此要对处于同步状态的Kuramoto 模型做出一定的调整，确保系统中各振荡器在周期震荡时所输出的相位差是固定的。为便于描述各振荡器的相位迟滞或阻挫，现定义φmn为相位差，表示振子n与m间的相位差，并代入式(1)。又因在实际工况中系统中的电机都是以2π 为周期，故对自然频率wm做出更改，令其为2πp(p为自然频率)，再对耦合系数进行更改，令wnm=k/N。则此时的KM 模型为

1.2 虚拟控制的振荡器网络搭建与步态参数映射

本文研究的机器人4 条腿是对称分布，每条腿对应各自的振荡器模型，机器人在行走时各腿部驱动关节处的相位是呈现规律性变化关系的，此时各腿的振荡器模型完成输出和每个驱动关节的映射关系。又因在Kuramoto 模型中θm的输出量是一条直线，且单调递增，并不适用于机器人的关节控制和驱动。故本文振荡器网络需要引入正弦函数来对其输出进行调整。

本文四足移动军用机器人单腿机构为3-UPS机构，其控制网络结构如图4 所示，从中可知控制网络中振子间均设计为双向对称形式，故振子间耦合强度均为wnm=wmn=1，同时相位差均为φmn=-φnm= π/12。

图4 非线性振子耦合网络Fig. 4 Coupled nonlinear oscillator network

单腿机构的简单控制网络完成搭建后，就要对KM 模型的主要参数进行分析确定，完成其输出的角度映射。以右前腿向右的步进运动为例，对其进行分解并投影，如图5 所示。图5 中，S为步长，Am、Lm分别表示腿部的转动电机幅值和推杆电机长度均处于最大值，Bm为腿部的次长分支转动电机幅值，L、h分别表示腿部足端距髋关节和离地最高高度。

图5 单腿周期行走图Fig. 5 Diagram of periodic walking of a single leg

当机器人的支撑相为右前腿时，这时腿部的转动电机幅值和推杆电机长度均处于最大值处，分别用Lm和Am表示，机体依靠关节电机的驱动使机体前移S/2，然后右前腿离地成为摆动相，其他腿触地成支撑相。由机器人的腿部结构分析可知，只有当机器人侧向迈腿时，上平台的驱动电机才会转动，向前迈腿时是不转动的，腿部关节电机幅值的投影才是其幅值Am。图6 所示为实际关节角度图。图6 中，单腿各分支在水平轴的投影用a表示；旋转轴与水平面的夹角为60°，用α表示。则幅值Amax的实际值为

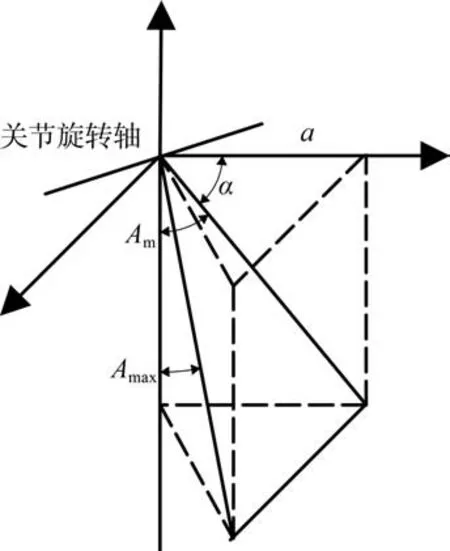
图6 实际关节角度图Fig. 6 Diagram of actual joint angle

再由腿部分解图可以得出：

为使幅值对称，选择初始角度(Amax+Bmax)/2作为平衡点，则另外两个腿部关节角度与驱动扭矩的关系式为

基于对机体腿部运动的研究发现，腿部的电动推杆的运动周期可划分为两个大运动周期，每个大运动周期包含一个小运动周期。当处于大周期内时，支撑相和摆动相运动的幅值不同；当处于小周期内时，伸缩杆的最短值相同，但最长值不同。

由图5 知当其为支撑相时，令Lm为最长幅值，Lsm为次长值大小，则最小幅值为Ls=LmcosAmax，且腿部支撑相与摆动相相位差了半个周期。本文选定支撑相的初始长度设为(Lm+Ls)/2，则腿部各分支的长度表达式为

式中：T为运动周期。

当腿部处于摆动相时，其最低幅值变为Lmin=L-h，选择初始长度为(Lm+Lmin)/2，则腿部各分支长度表达式和转动电机表达式分别为

式中：f0(θ)为初始驱动扭矩值。

由此就可以确定取不同的步长和机体高度时的运动参数，可以用表1 和表2 将数据结果表示出来。

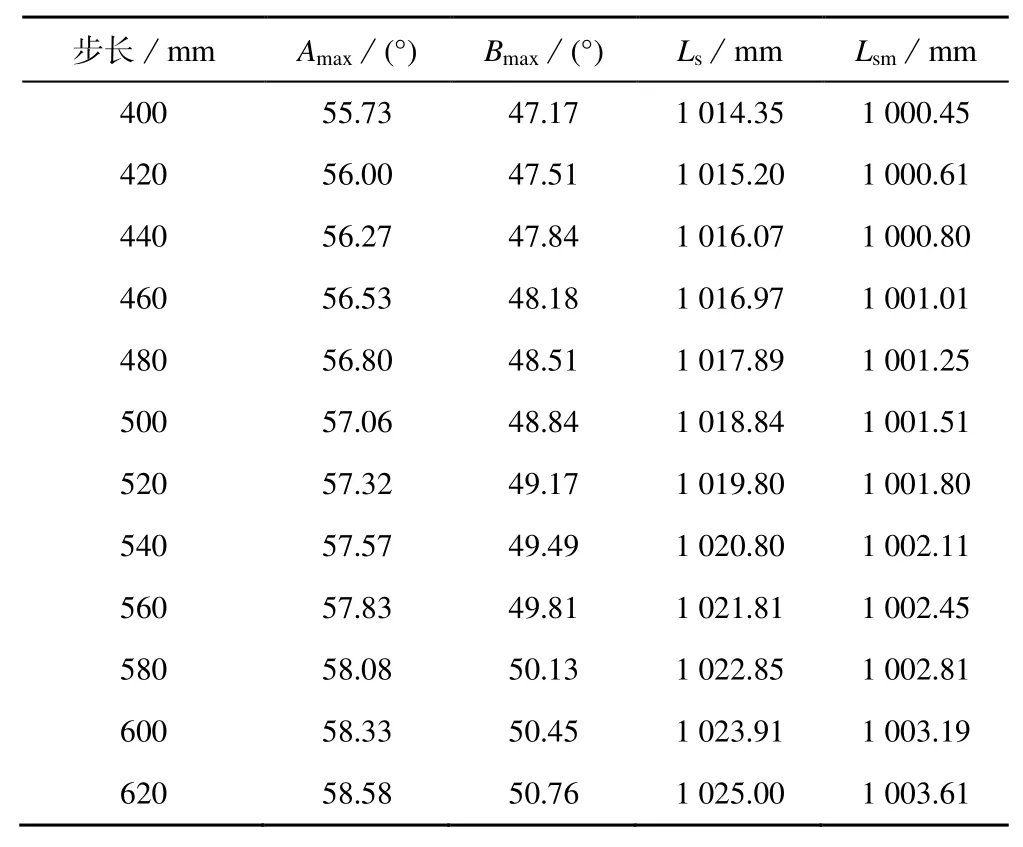
表1 步长与关节摆角关系Table 1 Relationship between step size and joint swing angle

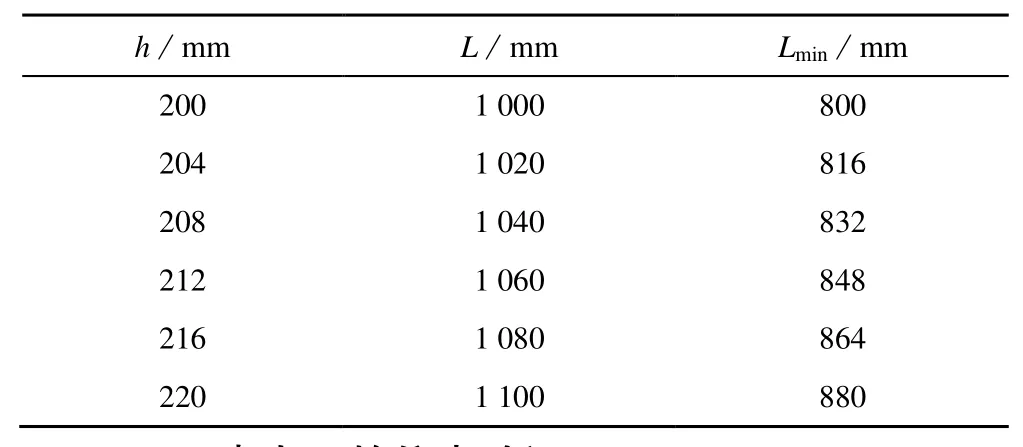
表2 抬腿高度与伸缩杆长度关系Table 2 Relationship between leg height and telescopic rod length

1.3 Trot 步态下的仿真验证

通过观察自然界中的四足动物可知，动物们的运动步态分 walk、trot、pace 和 gallop 4 种形 式[14-16]，且不管采用哪种运动步态行走，各腿之间均有着一定相位关系。本文把动物的各种步态运用到四足机器人上，并对这4种步态进行对比，发现比较常见的是trot 步态。故本文采用了对角腿相位相同的trot 步态，该步态会一直有2 条腿是支撑相，且与另外2条腿始终相隔半个周期，同时此种步态行走速度比较快，可用相位差矩阵表示出的步态时序为

本文令直线驱动电机Lmax= 1000 mm，Lmin= 500 mm 。小周期杆长为Lsm= 900 mm，步长选定540 mm，抬腿高度180 mm，耦合系数假定为500，以2 s 为周期，以0.1 为自然频率，经计算行走速度为 0.27 m/s，Amax= 22°，Bmax=-11°，Ls=788 mm，Lmin= 622 mm。则trot 步态的KM 网络表达式为

此时以trot 步态行走的机器人KM 物理模型就可由Simulink 软件进行搭建，其整体框架如图7所示，输出结果如图8、图9 所示。

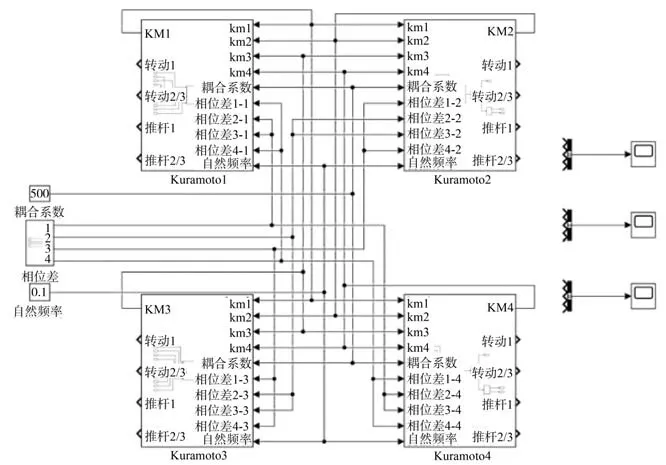
图7 非线性振子耦合网络图Fig. 7 Diagram of coupled nonlinear oscillator network

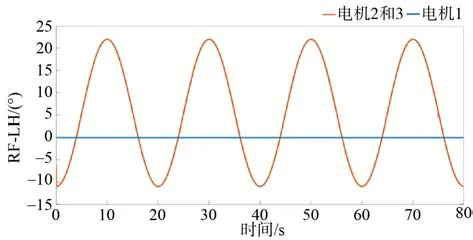
图8 trot 步态转动电机输出曲线图Fig. 8 Output curve of the trot motor

图9 Trot 步态直线电机输出曲线图Fig. 9 Output curve of the trot linear motor

因为电机2 和电机3 关于电机1 对称分布，所以电机 2 和电机 3 的输出曲线是一致的。从 图7~图9 中可知，虽然机器人的耦合非线性KM网络能很好地规划出驱动电机的移动曲线，但在实际行走过程中却把复杂的环境忽略了，会使机器人拥有较为僵硬的行走方式，这些会对机器人的机体和电机的使用寿命造成很大的损伤。为了让机器人的运动更加柔顺，就要在规划电机曲线时把缓冲量加入到其与实际的电机控制中，从而确保在遇到复杂的路况时，机器人能更好的进行适应。

在实际中，可把四足动物的单腿关节进行简化，当作一个弹簧阻尼器，同时提高阻尼系数以保证仿真结果的稳定性。本文机器人单腿将引入弹簧阻尼器来完成非线性KM 网络的输出量与扭矩的转化，这样就可以在控制机器人移动的同时，实现对机器人姿态的调整。但对于降低机器人因遇意外所产生的冲击力，就需在各驱动关节角与期望值间虚拟增设弹簧阻尼模型，且此关节力矩控制也保障了机器人各关节的扭矩输出。而关节的输出力矩随着足端期望角度的变化使得主动驱动关节随期望关节角度对足端轨迹进行输出。则此时机器人的腿部力矩输出为

式中：Kqi、Bqi分别为跟随的转动关节弹性系数和阻尼系数；φqd、φ˙qd分别为转动关节期望的角度和角速度；分别为跟随的转动关节期望的角度和角速度；Kli、Bli分别为跟随的直线驱动关节弹性系数和阻尼系数；分别为期望的直线驱动关节长度和速度。

3 基于虚拟模型控制的姿态调整

3.1 俯仰角调整

以搭建虚拟机械部件的方式来模拟机构同外界环境的交互运动为核心的虚拟模型控制就是对交互行为进行描述的模型，其仅依靠机器人当前状态即关节角度和速度再加上虚拟组件的状态就可实现对机器人行为的控制，通过阻尼器和弹簧等虚拟组件简化机体结构并与外界环境建立交互，应用更为简洁的操作步骤实现对机器人机体运动的有效控制。为预防机器人航向偏离预定方向、机体在对角轴上出现剧烈翻转和机体出现过大的倾斜角度等情况的发生，就需对机器人的航向、姿态、对角轴等方面进行机体姿态调整。

本文四足机器人能够实现在自身坐标系中的 3 个转动和3 个平动共6 个自由度的运动，为能全方位对机器人进行控制，需要充分研究机体的平动和转动情况。但因存在于模型中的虚拟力在现实中是不存在的，故机器人是依靠腿部驱动关节来实现机体的运动。而将足端的力映射为各驱动关节工作空间的关节驱动力矩，需要用到各驱动关节的速度雅可比矩阵，其表达式为

式中：θ1~θ6分别为机器人腿部各驱动关节的速度；v为机器人腿部线速度；w为机器人腿部角速度。

依虚功原理得各关节驱动力和足端驱动力各自所做虚功总和是相等的，即

式中：τ1~τ6分别为机器人腿部各关节的驱动力；Fp为机器人的足端虚拟力。

将式(16)与式(17)联立，得各关节驱动力与足端虚拟力的关系式为

机器人在运动时的俯仰角是通过调整机体绕侧向轴的虚拟力矩来控制机体相对足端连线平面的倾斜角度。本文设定支撑相的足端连线与机体质心所构成的平面为机体标准面，并将机体躯干面通过弹簧阻尼虚拟组件与其进行相连，且定义机体标准面与躯干面的夹角为相对俯仰角φy，通过测量计算弹簧组件被压缩或拉伸的大小来反映机体的倾斜程度。当机体绕质心发生转动使机体躯干倾斜时，这时俯仰角φy和由虚拟弹簧模型产生的虚拟力都会发生改变，因此机体的后支撑相分配来的足端虚拟接触力也会发生改变，就会对机体的俯仰角进行调整，最终会使机体与机体标准面相平行，如图10所示。图10 中，x轴表示机体前进方向，z轴表示机体竖直向上方向，xF、zF分别为竖直方向上前支撑相与后支撑相的坐标，xH、zH分别为x轴方向上前支撑相与后支撑相的坐标。

图10 机体俯仰角调整图Fig. 10 Diagram of pitch angle adjustment of the body

机器人机体俯仰角公式：

当机器人遇崎岖路况时，会要求机体平面与标准面之间保持一定角度不变，因此由躯干质心处的弹簧阻尼模型通过相对俯仰角的变化而在机体侧向轴上生成的虚拟力矩Ty为

式中：Kφy、Bφy为弹簧阻尼模型的弹性系数和阻尼系数；φyd为机体相对俯仰角期望值。但在实际情况下，机器人机体一般都要与足端连线相平行，此时虚拟力矩Ty为

3.2 对角轴翻滚

关于应用小跑步态的四足机器人的很多研究表明，机器人机体会绕对角支撑相发生转动是由于在髋关节处生成的反作用力矩影响的。遇到这种情况时，机体的两对角摆动相会有一个提前着地，这种异常着地虽会被耦合非线性振子网络进行纠正，但此时的反作用力矩无法保证机体trot 步态的稳定性，且过大的足端着地冲击力会在一定程度上损坏相应的电机，同时还会加重机体失稳的情况，甚至会使机器人的可靠性受到严重影响。

通过研究发现使机器人发生翻转的主要原因有两个，一个是因为机器人在向前行走时的两支撑相会使机体绕髋关节处生成力矩，如图11 所示，对此力矩在对角轴方向和与对角轴垂直的方向上进行分解，其中在质心处两沿对角轴方向的合力矩会造成机器人沿对角轴发生翻转的情况发生，翻转方向可由右手定则的母指指向确定。另一个是因为移动的机器人会在机体质心处绕对角支撑相产生一定的倾覆力矩，此部分力矩可被惯性力矩平衡掉，或者采用某种方法消除掉，如姿态调整和附加重量的方法。由此可知两个原因中前者对机器人的稳定运行产生的影响最大。

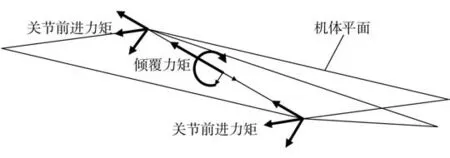
图11 倾覆力矩图Fig. 11 Overturning moment diagram

由KM 模型输出的曲线可知，在机器人前进的过程中，位于髋关节处的侧向转动电机是不发挥功能的，其最主要功能是通过改变机体腿部与竖直方向的夹角使机器人更大程度地适应不同倾斜程度的地面，当机器人向前运动时其输出的力矩可抵消掉引起机体倾覆的这部分关节输出力矩，以提高机器人的防侧翻能力。因而机器人是借助由弹簧阻尼模型生成的虚拟力矩来对变化的横滚角进行修正，如图12 所示。

图12 修正力矩图Fig. 12 Corrected moment diagram

本文中机器人通过在机构中安装陀螺仪的方法来达到随时纠正机体绕对角轴倾斜的目的，当机体移动时用陀螺仪采集机体绕轴的角速度和角加速度，最后由虚拟弹簧阻尼模型输出的虚拟力矩对倾覆力矩进行修正。通常对机体横滚角的期望值为零，此时的虚拟力矩为

式中：Kφx、Bφx为弹簧阻尼模型的弹性系数和阻尼系数；φx为机体横滚角期望值。

3.3 方向控制

要保证机器人能始终不改变预定的运动方向，就要实时对机器人在航向的偏差量进行调整。本文机器人腿部机构的自由度为6，因此在机器人的行进过程中机体可借助两支撑相的足端反方向的侧向接触力实现对机体质心处绕z轴扭矩的调整，即对机体前进方向的调整是依靠支撑相反方向的虚拟力生成的侧向速度实现的。依然使用虚拟弹簧阻尼模型对偏航角进行纠正，则式(23)为在机器人机体质心处生成的控制虚拟力矩的表达式：

式中：Kφz、Bφz为弹簧阻尼模型的弹性系数和阻尼系数；φzd为转动关节期望的角度；φz为机体偏航角期望值。

当在机器人的行进过程中机体出现偏移量φz时，两支撑相的足端反方向的侧向虚拟力可实现对机体质心处绕z轴扭矩的调整来纠正机体的偏移量。然后机体随φz的变化实时调整足端位移和侧向速度来使机体转动，保证机器人按预定的方向运动。但当机器人受到侧向冲击时，虚拟模型会在短暂的时间内调整前进方向，且在侧向速度降低时回到正确方向。

3.4 高度调整与斜坡适应

当机器人在斜坡上行走时，其重心在竖直方向上的投影都会落在后支撑相周围，此时由于重力的影响，机体会出现“后仰”现象，此时机体后支撑相将承担其全部重力，而前支撑相会因与斜坡摩擦力不足出现打滑现象，更严重时会出现前支撑相直接离地的现象，如图13(a)所示。为预防此种情况，本文采用姿态传感器随时对机体重心位置进行调整，保证机体重力在前后支撑相上的分配更均衡。故在斜坡上运动时，要使机器人的足端着地点在髋关节的坐标原点处有偏移量产生，让其重心在竖直方向上的投影都能落在后支撑相着地点周围，使前后支撑相所承担的重力差变小，让机体的稳定性尽可能得到提高，调整过程如图13所示。图13中，θ为机体躯干与斜坡的夹角，y轴为机体前进方向，z轴为垂直于机体竖直向上，Dy为足端落地点相对于髋关节坐标原点的偏移量。

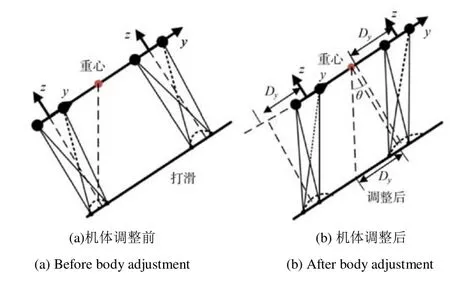
图13 修正力矩图Fig. 13 Corrected moment diagram

首先要借助支撑相对预期的机体高度实施调整，而机器人两支撑相的髋关节高度的平均值就是机体的高度值。这里依然需要借助弹簧阻尼模型来完成针对机体腿部高度的调整，而在竖直方向上对机体速度的期望值通常为零，此时的虚拟力为

式中：Kh、Bh为弹簧阻尼模型的弹性系数和阻尼系数；hzd为转动关节在竖直方向上的期望高度。

对机体的偏移完成修正后，这时支撑相高度的平均值就是机器人质心的高度值，以小跑步态为例也就是两支撑相的平均高度，则预期的支撑相足端偏移量表达式为

式中：Y为支撑相足端实际偏移量。

当机器人在斜坡上运动时，机器人经由足端预期落地点和实际落地点间的偏移来对机器人重心进行调整，让其始终在支撑相中心处附近，这样使得机器人的爬坡稳定性会增加，还能在一定程度上预防足端打滑现象的发生。由增益控制器对足端偏移量进行映射，得到可以对其进行调整的力矩，则此时的修正力矩为

式中：Kx为增益控制器的调整系数。

4 四足移动军用机器人整机步态控制规划

4.1 虚拟力的分配

本文中机器人控制机体实现设定的预期运动状态的虚拟力是由虚拟弹簧阻尼模型产生的，然而这些虚拟力是如何使机体单腿分支上的主动驱动关节执行出来需要进一步研究。由于机器人各腿足端的虚拟力不相同，在主动关节处产生的驱动力矩也不同，因此需要一种虚拟力的分配机制将控制机体运动状态的虚拟力分配到不同腿上由此映射出这些虚拟力所需要的关节力矩。目前对这些虚拟力进行平均分配到机器人四条腿的足端处是最简单的方法，但由于处在动态行走中的机器人是欠驱动的，例如使用trot 步态的机器人在移动时同时只有两腿着地，这时虚拟力的分配就不再是简单的四等分了。而本文中对应用trot 步态的机器人足端虚拟力的调配问题借助了静力学分析法进行确定，其中机体的各虚拟力如图14 所示。图14 中，fF,x、fF,y、fF,z为前肢足端虚拟力在3 个坐标轴上的分量，fH,x、fH,y、fH,z为后肢足端虚拟力在3 个坐标轴上的分量。

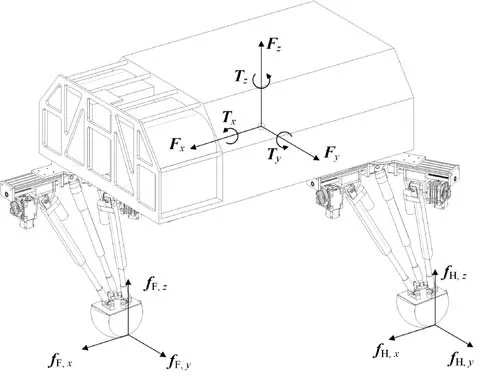
图14 非线性振子耦合网络图Fig. 14 Diagram of coupled nonlinear oscillator network

首先对处于trot 步态的机器人进行整体受力分析，设机体每条腿的重力都作用于其静态平台中心处，四条腿的重力和即为机体所受的合力，然后把合力分解为沿垂直方向向下的机体重力GB与4 条腿相同的简化重力Gi(i=1、2、3、4)5 个部分。再将这五部分力在各自坐标系中沿坐标轴进行分解，但因相同的腿部简化重力在机体质心处的和力矩为 0 N·m，为预防奇异矩阵的出现，本文将在机体运动方向上的3 个虚拟力也在其坐标系中标出。则作用在机体质心处的虚拟力矩与虚拟力的求解表达式为

式中：Gx、Gy、Gz为机体重力在x、y、z轴上的分量；xH、yH、zH为机体支撑相后足端虚拟力在x、y、z轴上的分量；xF、yF、zF为机体支撑相前足端虚拟力在x、y、z轴上的分量。当机器人运动时，一般都会令其横滚角φx=0，这样在y轴方向上的机器人机体重力会为0 N，但受俯仰角yφ的影响，则在x、y、z轴方向上机器人的重力大小分 别为

式中：M为机器人质量；g为重力加速度。则支撑相的足端虚拟力可由式(28)求出，再将式(28)改写为矩阵形式，有

观察式(29)的系数矩阵可发现，其秩为5 而非满秩，这表明仅靠机器人支撑相的足端虚拟力是实现不了机器人机体全方位运动控制的，要想实现机器人的全方位控制就得先限制机器人的某些运动状态控制，然后再对机器人的虚拟力进行求解。而对自然界中四足动物的观察还可发现，当其目的地在其身体侧面的某一位置时，动物们并不会直接进行侧向移动，而是先旋转自身方向再进行移动，所以本文认为侧向移动对机器人来说作用不大，故选择侧向虚拟力Fy进行限制，针对Fy添加约束条件fF,y=fH,y后，式(29)变为

观察式(30)可发现其系数矩阵不为0，其必存在逆矩阵，则对式(30)的系数矩阵求逆再与机体控制虚拟力相乘可得机器人各腿足端点的虚拟力。而事实上本文机器人已用非线性振荡器网络得出了其向前运动时所需的主动驱动力矩，并没有用到机体质心处的虚拟力，只是将控制机器人姿态的虚拟扭矩和控制机身高度的虚拟力进行了映射，故选取系数矩阵的逆矩阵中虚拟扭矩所对应的后5 列即可。但当处于行走中的机器人受到侧向冲击时，机器人的增益控制器就会为缩短响应时间直接输出与侧向冲击力速度有关的足端虚拟力fF,y=fH,y=ky·vy/2 (ky为增益控制器的调整系数)，此时足端虚拟力为

式中：qij(i=1, ···, 5,j=1,···, 6)为系数矩阵的第i行第j列的元素。

确定了机器人各腿的足端虚拟力后，再借助虚功原理把它反映成主动驱动力矩，则控制机体姿态的单腿驱动力矩：

式中：Q表示系数矩阵。

进一步，此方法也可应用到机器人支撑相为多足时的步态算法中。

4.2 整体步态控制

本文中基于Kuramoto 非线性振荡器的中央模式控制生成四足机器人运动所需的基础信息，关节力矩则由弹簧阻尼模型生成。考虑到处于运动状态的机器人需要对其自身姿态、着地角度和运动方向的调整，本文采用虚拟组件对处于运动状态的腿部各关节交互力的偏差量实时检测，通过虚拟模型控制计算出修正偏差，由其校正因处于不同步态时非线性振子产生的各关节输出量，其整体控制框如 图15 所示。

由图15 可知，先是由KM 控制网络产生步态控制信息，再经弹簧阻尼模型输出为各关节力矩，由其控制机器人摆动腿的运动轨迹和时序。机器人也会随时把支撑相的各姿态信息向姿态控制器发送，机器人再经虚拟模型算出调整机体姿态所需的虚拟力，对其分配就能得到控制机器人姿态的各关节力矩，这些力矩和由KM 控制网络生成力矩一起对机器人的运动进行控制。

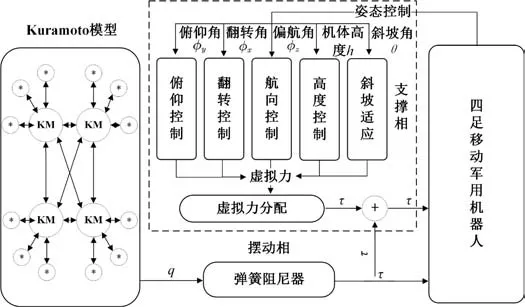
图15 步态规划整体框图Fig. 15 Overall block diagram of gait planning

5 控制算法虚拟仿真验证

5.1 V-REP 中虚拟样机搭建

基于第3、4 节的研究，下面就军用机器人的步态控制算法进行验证，看其能否稳定且有效地对机器人的运动进行控制。首先将本文中机器人的虚拟样机模型在V-REP 软件中完成搭建，并把验证移动控制算法所需要的仿真环境建好，通过仿真软件监测本文中机器人处于不同运动状态时的各种数据以及关于稳定裕度的变化，再由分析得到的各种数据来判断此控制算法能否稳定且有效的对机器人进行控制[17-20]。

四足移动军用机器人的三维模型已经在SolidWorks 软件中设计完成，而要想在V-REP 中实现对三维模型的仿真，就需要在V-REP 软件中按照实体–关节–实体的顺序重新构建一个带有各构件间依赖关系的机器人虚拟模型，最终模型如图16所示。

图16 最终模型图Fig. 16 Final model drawing

最后，为测得机器人各足端的接触力和机器人在移动过程中的姿态角，还需在模型各足端处和模型中心处均加上传感器。

5.2 步态控制算法验证

为简化仿真操作，本文利用MATLAB 软件Simulink 中的控制模型直接控制V-REP 中的虚拟样机。本文采用Simulink 软件中Function 直接调用V-REP 中的remoteAPI 连接库同外部程序进行通讯[21-22]，即步态控制模型在Simulink 中就完成了搭建，再由Simulink 与V-REP 通信以达到控制V-REP 中的虚拟模型运动对其步态控制策略进行验正的目的，则整体模型框架如图17 所示。

图17 步态控制模型Fig. 17 Gait control model

由图17 可知，步态控制模型的左上角连接VREP，启动时由 V-REP 计算的数据会实时向MATLAB 中发送；KM 中央模型发生器位于模型上半部分，其功能为计算出机器人行走时的各关节位移，并由弹簧阻尼器将其映射成关节扭矩后再输出；模型的下半部分用来对机器人的行走状态进行控制，由位于V-REP 中的传感器把采集到的数据返回到MATLAB 软件，由虚拟模型计算出机器人保持预期状态所需要的虚拟力矩，然后把控制各关节进行调整的力矩经由静力学平衡进行分配，再把中央模型发生器产生的力矩和状态检测得到的支撑相力矩结合，最后对实时传入V-REP 中由模型计算出的力矩进行仿真。

5.3 平坦路面行走仿真验证

首先要对处于正常行走状态的机器人应用步态控制算法测出其各项运动参数。然后对在V-REP 中虚拟样机应用在MATLAB 软件中搭建的步态控制算法进行平坦地面行走仿真，如图18 所示。此时在trot 步态下机器人的前进速度为0.5 m/s，由图18 可知位于机器人机体上对角线方位的机械腿动作是一致的，相互交替使机器人平稳向前运动，且在仿真过程中未出现使机器人机体震颤或摔倒的情况。

图18 平地实验Fig. 18 Ground experiment

为保证机器人能够稳定的运行，V-REP 需要把机体姿态角随时向位于MATLAB 软件中的步态控制器发送，保证实时输出足端虚拟力。当机器人处于行走状态时，机体的各个姿态角和高度的检测值变化情况如图19 所示。

由图19 可知，机器人机体的姿态角均存在误差，且为周期性的，都是因为在步行状态中机器人抬腿、落腿等动作生成的难以回避的误差，但误差值均在-1°~1°之间；由图19(d)可知，机身高度的误差最小。因此可知本文机器人能保证机体按照规划好的航向和身体姿态稳定的进行运动，机体速度和足端冲击力如图20 所示。

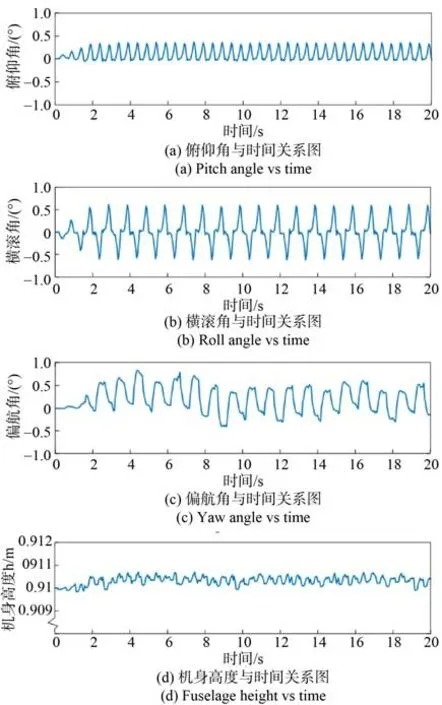
图19 机体姿态与高度Fig. 19 Body attitude and altitude

由图20(a)可知，机体前进速度会随机器人的运动状态发生变化，在最开始的几秒内，机器人由静止状态到快步提速然后速度趋于稳定；由 图20(b)可知，因机器人足端不停的在触地-分离间转换，会使机体侧向速度产生很小的瞬时误差； 由图20(c)可知，机体竖直方向速度会因周期性出现的左前足端冲击力的影响产生最大0.05 m/s左右的误差，可忽略不计。由此可得本文机器人在行走过程中能保证机体的平稳，不会使机体发生速度突变和机身倾斜的情况。

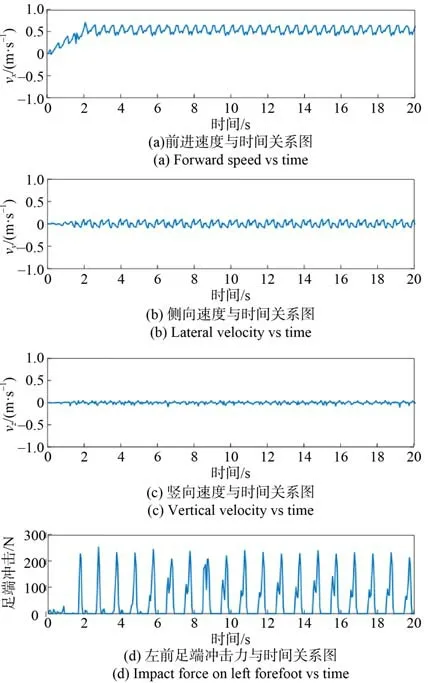
图20 机体速度与足端力Fig. 20 Body speed and foot force

5.4 斜坡行走仿真验证

下面对处于斜坡行走的机器人进行适应能力验证。首先在实验环境中设立一个倾角为6°的斜坡，然后对迈入斜坡和在斜坡上运动时机器人的各项运动参数进行观察，仿真结果如图21 所示。

图21 斜坡实验Fig. 21 Slope experiment

当机器人迈入斜坡时，机体各个姿态角和高度的检测值变化情况如图22 所示。

图22 机体姿态与高度Fig. 22 Body attitude and altitude

从图22中可知，机身的俯仰角会在机器人迈入斜坡时发生骤降，担当机器人全部机身迈入斜坡后，机身的俯仰角会稳定在与斜坡倾角相同的6°左右，达到新的平衡状态。由图22(c)得知，机身的行走的趋势因不确定的足端接触力会向左侧倾斜，随后又因虚拟力的作用机体又会向右产生倾斜，最终机体会沿原定角度行走；由图22(d)可知，在爬坡过程中机器人机体始终保持稳定的移动状态。机器人速度曲线如图23所示。

从图23中得知：除在刚踏入斜坡时机体速度会产生不稳定变化外，都能保证机体速度的平稳，但由于斜坡的影响，在竖直方向机体会产生一个稳定且不在为0 m/s的速度；除在刚踏入斜坡时机器人因步态调整产生了较大的接触力外，都能保证机体的平稳运行。

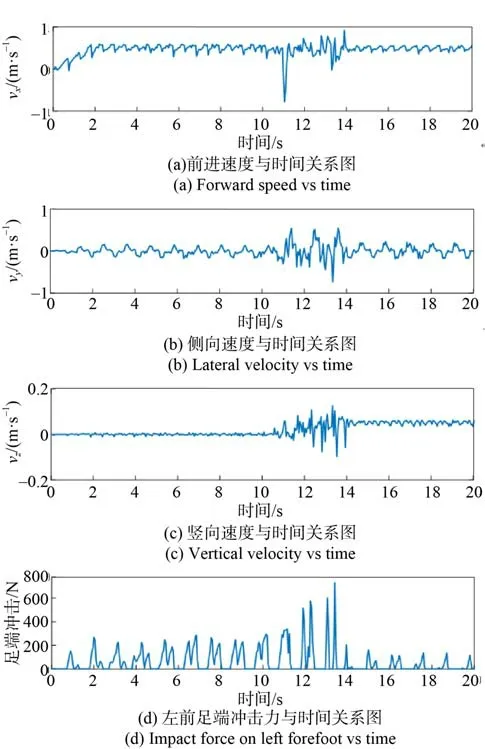
图23 机体速度与足端力Fig. 23 Body speed and foot force

5.5 侧向冲击仿真验证

四足机器人在行走过程中，由于机身长度一般大于机身宽度，故机体在受到侧面冲击时会产生更大的颠覆力矩。本文拟用钟摆锤模拟机身侧面的冲击力来测试机器人的稳定性，钟摆锤重40 kg，摆绳长0.6 m，初始角度为60°，则发生撞击时速度为2.5 m/s，冲量为100 kg·m/s。当机器人的速度与姿态角受冲击而失去稳定性时，由控制器中虚拟模型计算出用来恢复机体平衡所需的足端虚拟力，实验过程如图24所示。

图24 冲击实验Fig. 24 Impact test

当机器人遭受侧向冲击力作用时，机体各个姿态角和高度的检测值变化情况如图25所示。

从图25(a)中得知，机身的俯仰角会骤降同时机体后仰，但因误差的存在，这时由虚拟模型生成的足端虚拟力可使机体向后仰的趋势减弱，并最后使机体慢慢恢复平衡状态。从图25(b)中得知，机身横滚角因冲击力的影响瞬时产生一个反向偏角，且与机身前进方向一致，用来对开始侧移的机身进行修正，并最终恢复到原来的稳定状态。从 图25(c)中得知，因本文假设冲击力作用于机器人的前半身处，故在行进方向上机器人偏航角的瞬时偏差最大能达20°左右，会与原前进方向产生偏离，但随机体足端虚拟力对偏航角的调整，最终机器人的行进方向又恢复原方向上。其速度曲线如 图26所示。

图25 机体姿态与高度Fig. 25 Body attitude and altitude

从图26(a)中得知，机器人的前进速度因冲击的影响发生骤降，但随机体腿部姿态的调整，最终机器人的行进速度恢复到原来的稳定状态。由于机体受到的冲击来自侧面，故图26(b)中的速度值变化最明显，突变峰值可达2 m/s，此时机器人因与预期速度产生偏离，机体会通过持续对足端虚拟力进行调整来纠正机体的侧向速度，一定时间后侧向速度会趋于0 m/s，机体恢复到正常状态。从 图26(c)和图26(d)中可知，竖向速度的剧变同姿态角相同，机体刚受到冲击力时就会瞬时后仰，此时速度发生突变，然后随着机体姿态的不断调整速度也在不断变化，并最终恢复到正常状态。

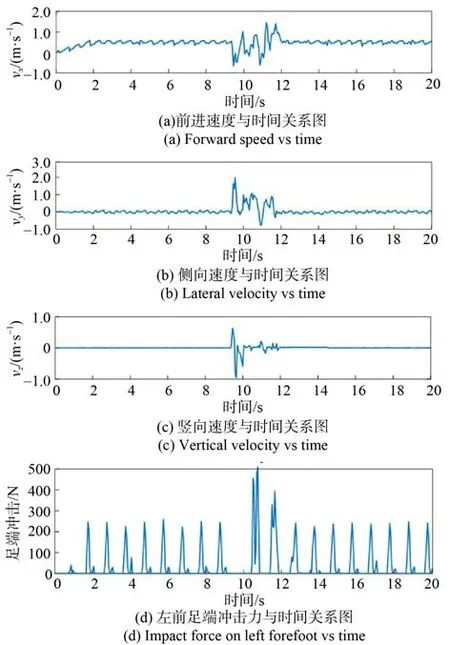
图26 机体速度与足端力Fig. 26 Body speed and foot force

6 结论

本文在四足移动军用机器人控制上把基于CPG 的控制方法和基于虚拟模型的控制方法进行综合，为四足军用机器人的步态行走控制设计了一种新型控制模式，在V-REP 软件中搭建出虚拟样机，在Simulink 软件中搭建出步态控制算法的框架，通过V-REP 与MATLAB 软件对该虚拟样机步态进行联合实验仿真。仿真结果验证了这种步态控制算法的有效性，在简化控制网络的同时还能保证机器人在行走过程中拥有较强的灵活性和抗干扰能力，这种新型控制模式也为四足并联军用机器人的步态控制提供了新的思路与方法。