基于PBD 算法的海上补给装备柔性体仿真技术

李楠, 任鸿翔

(1. 海军勤务学院，天津 300450; 2. 大连海事大学，辽宁 大连 116085)

0 引言

海上补给是提升海军舰艇的续航力和作战半径的有效手段[1]。海上补给装备系统复杂，技术要求高，训练难度大。开展仿真训练成本较低、效率较高。目前开发的海上补给仿真训练系统在训练架设索道的环节中，一般采用两端挂点实时距离计算并进行直线连点的方式[2]，与补给实际过程严重不符，无法模拟由于横风载荷和船体摇摆等带来的索具振动，导致官兵在训练时，无法开展索具振动控制技术训练。

索具等柔性物体建模的研究始于20 世纪初，在当时的计算条件和数值仿真技术条件下，对索具的研究仅限于稳态特性。随着计算机计算性能的大幅提升，对索具的研究也有了深入提高。目前索具类柔性体主要使用的动力学模型包括：静力学平面非线性模型、质量弹簧系统模型、有限元模型和多体动力学模型等[3]。

基于位置动力学(PBD)算法具有稳定性强、允许较大的时间步长以及较好的收敛性等优点。本文从多体动力学模型出发，建立补给装备索具柔性体模型，并运用PBD 算法开展海上补给装备索具视景仿真研究，旨在提高海上补给仿真训练系统的真实感和训练效能。

1 海上补给装备柔性体仿真建模

1.1 索具多体动力学模型

索具多体动力学模型是将绳索离散成若干索具段，每个索具段视为刚体，各索具段之间由连接件连接便可建立一个多刚体系统[4]。

索具多刚体动力学模型的基础上，在索具单元之间的连接件上添加适当的阻尼和弹性形变，如平移阻尼、平移刚度、旋转阻尼、旋转刚度阵等几种矩阵，使刚体单元之间的联接变成柔性连接，从而将索具的多刚体动力学模型转化为索具刚柔混合动力学模型[5]。

在此基础上，进一步将各索具单元进行柔性处理成为具备6 阶模态向量的柔性简支梁，刚柔混合体系统就转换成了多柔体系统[6-7]。

海上补给装备柔性体包括高架索、牵引索、输油软管等，动力学特性均与绳索相近。因此，本文采用索具多体动力学模型建模方法进行海上补给装备柔性体视景仿真建模。

1.2 海上补给装备柔性体视景仿真建模

海上补给装备中柔性体包括输油软管、高架索、牵索、引缆等。其运动形式属于三维动态运动，为准确反映其运动，在建模时将索具视为刚柔混合体系统。如图2 所示，将索具在空间上离散为N段单元索具段，索具段之间通过无质量的质点连接，将所有外载荷(阻力、重力、浮力等)的作用集中到索具段上，并计入惯性质量的影响，建立索具段点的运动方程组，通过相应的数值计算方法求[8-10]。

应用牛顿第二定律，得到索具节点的基本运动控制方程：

式中：Mi为索具节点的质量矩阵，包括索具节点自身的惯性质量mi和其在流体中的附加质量Mai；为第i个节点的加速度；Fi为作用于节点i上的外力，包括索具节点的张力ΔTi、内部阻尼力ΔCi、浮力Bi和重力Gi等。式(1)中的mi、可以表示为

式中：Pi为3×3 阶单位矩阵，ωi为绳索单元转动惯量；ln为节点间未拉伸长度；ρ为绳索材料密度；Ca为附加质量系数；si为为微元段的横截面积；Pi为微元段在浮动坐标系上的投影，下标i-1/2和i+1/2 分别表示节点i-1 到i、节点i到i+1 之间的物理量，如li+1/2=si+1-si表示节点i到节点i+1 间的长度；θ、φ分别为浮动坐标系与地球坐标系之间的夹角。

索具动力学模型解算如图1 所示。

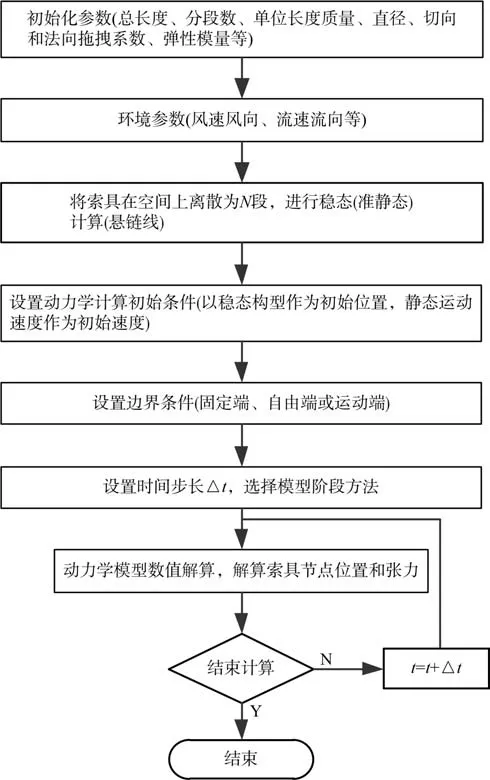
图1 柔性索具动力学模型解算流程Fig. 1 Computation flow of the dynamic model of the flexible rigging

2 海上补给装备柔性体视景仿真

利用多体动力学建立的海上补给装备索具等柔性体模型，通过计算，可以很好地反映索具的拉伸、弯曲、扭转等变形效应，但在三维可视化仿真中，实时解算仍存在迭代次数多、收敛难、失效性较差等问题，而在使用PBD 方法模拟索具，需要多次迭代才能使索具的距离约束条件收敛，容易引起模拟的索具产生弹性失真。本文在普通索具模拟的约束条件中增加长距离约束、引脚约束等约束，从而解决了海上补给装备柔性体在视景仿真中失真的问题。

2.1 PBD 算法概述

在PBD 方法中，索具用约束耦合的粒子表示，在每个时间步长中迭代地求解这些约束条件[11]。对索具粒子的模拟迭代计算分为3 个步骤：1)根据速度和外力移动索具粒子；2)使索具粒子满足约束条件；3)基于给定数据和时间步长Δt，执行时间 积分。

索具粒子由N粒子和M个约束组成。粒子i∈[1, ···,N]的质量为mi、位置为xi和速度为xi，约束j∈[1, ···,M]有如下5 种特性：

1)约束基数nj，即第j个约束影响的粒子数目为nj。

3){i1,… ,inj}，ik∈ {1,… ,N}。

4)约束对应的刚度参数kj∈[ 0,1]。

5)约束类型分为单边约束Cj(xi1, …,xinj)≥0与双边约束。

在模拟步骤中初始化索具粒子的位置，速度和质量倒数。把所有不能转换为位置约束的力(如重力)记为fext(xi)，并根据fext(xi)的值进行一次数值积分预测速度vi。然后直接对速度进行衰减操作模拟阻尼。计算完速度后再计算位置的预测值pi。在迭代计算的每个时间步长中生成附加的碰撞约束Mcoll，碰撞顶点的数量决定了碰撞约束Mcoll的数量。得到M个内部约束和Mcoll个外部约束之后，对这些约束进行迭代求解，得到校正后的粒子位置。最后根据摩擦和恢复系数修改速度vi。

2.2 海上补给装备柔性体的约束设置与计算

海上补给装备柔性体在横风、船体摇摆、悬挂重物移动等外部载荷作用下，会出现拉升、弯曲、附着、碰撞等变形。能否在视景中逼真模拟以上各种柔性体变形是衡量海上补给仿真训练系统逼真度高低的重要指标[12]。

PBD 方法通过修改索具粒子的位置关系，可以模拟出索具等柔性体拉升、弯曲、附着、碰撞的变形。在模拟柔性体拉升、弯曲时，本文使用了拉伸约束、弯曲约束，避免了索具的过度拉伸和弯曲失真；在模拟柔性体和附着物连接时，使用了长距离附着物约束和单边引脚约束，避免了附着物的拉伸变形失真，附着物与柔性体连接点的两个粒子合并为一个粒子进行计算[13-14]。

2.2.1 海上补给装备柔性体拉伸约束的设置与计算

海上补给装备中的高架索是实施航行横向补给时作为承载质量的索具。在补给过程中，始终呈现紧张状态。在其上要悬挂输油软管鞍座或干货行车，并承受横风、船摇等载荷，因此，在仿真过程中，需要实时计算其张力，并保证其柔性拉伸状态随载荷变化而产生拉伸变形。本文使用拉伸约束，考虑高架索为钢索，抗拉伸能力强，因此设置拉伸约束系数为1，仿真效果如图2 所示。其中图2(a)显示的是高架索的组成粒子及受力情况(绿色矢量为高架索垂直方向上的力，黄色矢量为高架索水平方向上的力)，图2(b)为高架索组成粒子的蒙皮截图，图2(c)为高架索的仿真效果。

图2 海上补给装备高架索拉升效应视景仿真效果Fig. 2 Visual simulation results of the hoisting effect of the viaduct of the replenishment equipment

2.2.2 海上补给装备柔性体弯曲约束的设置与计算

除了拉伸效应外，在海上补给装备柔性体仿真中也要考虑弯曲效应。柔性体模型上3 个相邻粒子位置可以决定柔性体的弯曲效果。p1、p2、p3为柔性体3 个相邻粒子，以p1、p3连线为基准线，通过计算p2距基准线的距离来确定柔性体的弯矩程度。由于粒子数量和解算率的不同，可能会出现柔性体弯曲效果失真。为此需要增加弯曲约束来保证仿真效果。

输油(水)软管是海上补给装备，在横向补给过程中用于输送油(水)液货的柔性体设备。其具有高抗弯曲度但低拉伸刚度的物理特性，因此在添加拉伸约束和弯曲约束时，取拉伸约束值较低，约为0.5，取弯曲约束值较大，约为0.8，仿真效果如 图3所示。其中图3(a)显示的是输油软管的组成粒子及受力情况(绿色矢量为高架索垂直方向上的力，黄色矢量为高架索水平方向上的力)，图3(b)为输油软管组成粒子的蒙皮截图，图3(c)为输油软管的仿真效果。

图3 海上补给装备输油软管弯曲效应视景仿真效果Fig. 3 Visual simulation results of the bending effect of the oil hose of the replenishment equipment

2.2.3 海上补给装备柔性体长距离附着约束的设置与计算

海上补给装备柔性体通常存在自由端，且自由端会附着输油软管、货物、挂钩等设备，此时柔性体会随着附着物的运动而出现摆动。在使用PBD方法对上述存在附着物时柔性体的模拟中发现，若将附着物看作柔性体的末端节点进行迭代计算时，则容易产生附着物被一同拉升而出现弹性失真。长距离附着约束只计算从附着物与柔性体接触点粒子到柔性体自由粒子的整个路径的拉伸，不对附着物产生影响[15]。

海上干货补给是在高架索上设置行车，行车下部通过4 根吊带悬挂货物小车。4 根吊带属于柔性体，且作业过程中呈拉伸状态，而下部悬吊的货物小车属于刚体，在行车运行时，货物小车会出现摆动。若将货物小车与吊带看作一个整体进行柔性体仿真，则施加拉伸约束后，货物小车也会出现拉伸变形。因此，需要在货物小车与吊带之间添加长距离附着约束，从而实现具有附着物的吊带自由端在货物小车重力作用下自由摆动时不出现货物小车的变形失真。仿真效果如图4 所示。

图4 吊挂索具与吊筐之间的摆动效应的视景 仿真效果Fig. 4 Visual simulation results of the swing effect between the hanging rigging and the hanging basket

2.2.4 海上补给装备柔性体与附着物相互约束的设置与计算

海上补给装备柔性体端部一般都会连接附着物，如发射引缆。发射引缆是海上航行横向补给作业的第一步，目的是便于接收舰通过引缆接收高架索等索具。引缆是一根纤维软绳，前段挂有引缆球，通过撇缆枪发射到接收舰。发射引缆时，引缆随撇缆球到达接收舰的过程中，柔性体和附着物都可以进行3 自由度运动，且相互影响。为模拟柔性体与附着物相互作用，本文通过销子、销接头等引脚约束连接多个物体，引脚约束可以确保这些物体在每一个时间步长更新的位置与所连接物体的附着点位置一致。使用单边引脚约束，以确保物体顶点位于动态物体的外部，从而避免了物体之间穿透现象的产生。仿真效果如图5 所示。

图5 引缆与撇缆球之间的相互作用效应的视景 仿真效果Fig. 5 Visual simulation results of the interaction effect between the lead cable and the mooring ball

2.3 海上补给仿真训练时效性计算

在确定PBD 算法后，还需确定仿真迭代计算方法，用于确保在较少的迭代步数下，模型计算尽快收敛。PBD 算法通常采用非线性高斯-赛德尔或牛顿迭代法两种迭代算法进行计算。本文通过以下算例比较非线性高斯-赛德尔或牛顿迭代法两种迭代算法，确定海上补给柔性体仿真中迭代算法。

海上补给仿真训练系统将柔性体分段长度设为0.2 m，重力加速度为9.8 m/s2，比较非线性高斯-赛德尔迭代和牛顿迭代梁总算法的相对误差与迭代次数[16]，发现迭代次数相同的情况下，高斯-赛德尔迭代法在收敛速度上优于牛顿法，如表1 所示，采用两种不同的方法计算得到不同的迭代次数下所用的时间和对应的相对误差。从表1 中可以看出，在 5 次迭代计算时，PBD 方法得到的相对误差为9.02×10-3、耗时为28 ms，而牛顿迭代法得到的相对误差为4.5×10-2、耗时为422 ms。两种方法在5 次迭代内均已经能够满足仿真精度的需求，牛顿迭代算法更加耗时。因此，本文采用的高斯-赛德尔迭代方法在较低的迭代次数时能较好地满足仿真系统的要求，且表现出更好的稳定性能。从仿真实时性的角度考虑，此方法在交互应用中更具有优势。

表1 PBD 方法的性能结果Table 1 Performance results of the PBD method

2.4 海上补给仿真训练系统

本文从多体动力学模型出发，建立补给装备索具柔性体模型，并运用PBD 算法开展海上补给装备索具视景仿真研究，使用了拉伸约束、弯曲约束、长距离附着物约束和单边引脚约束，避免了变形失真。通过提高索具、输油软管等柔性体的动态逼真度，复现海上补给实际状态，并以此为基础研发了海上补给仿真训练系统，用于开展海上航行横向干、液货补给仿真训练[17-20]。

该系统为国内首套用于海上补给训练的仿真系统，可开展海上航行横向补给全流程训练。通过部队试用，反映出本文系统索具、输油软管等柔性体的动态逼真度极高，能够很好地复现海上补给实际状态，训练效果基本与实装训练一致，可有效提升海军部队海上补给的训练水平。

3 结论

本文针对海上补给仿真训练系统尚存在柔性体变形失真的问题，建立海上补给装备索具柔性体多体动力学仿真模型，通过增加拉伸约束、弯曲约束、长距离约束和附着物相互约束实现了柔性体的动态变形三维模拟。最后通过比较高斯-赛德尔与牛顿算法的实时计算效果，确定本文采用的高斯-赛德尔迭代方法来提高视景仿真的效果，避免因为计算时间长导致画面失真。最终开发出了海上补给仿真训练系统，极大地提高了系统的操作真实感，为海上补给专业官兵尽快形成战斗力提供了有效途径。