考虑高强度钢加工表面完整性的背应力能法疲劳寿命 预测模型

王永, 王西彬, 王志斌, 刘志兵, 刘书尧, 陈洪涛, 王湃

(1. 太原理工大学 机械与运载工程学院，山西 太原 030024; 2. 北京理工大学 机械与车辆学院，北京 100081; 3. 山西柴油机工业有限责任公司，山西 大同 037036)

0 引言

零部件在工程应用中一旦发生疲劳失效，将危机安全并引起严重的经济损失。目前，对疲劳寿命进行预测的方法主要包含应力法、临界面法和能量法等[1]。其中能量法从疲劳损伤机理的角度来对疲劳寿命进行预测，能够很好地解释疲劳断裂行为[2]，故得到广泛应用。机加工作为最终的制造工艺，为提高疲劳寿命，往往通过一味地减小加工表面应力集中系数、增大残余压应力等方式对加工表面层进行评价[3]，然而增加了零件制造工艺难度且降低了生产效率，因此急需定量描述加工表面完整性与疲劳行为之间的映射关系[4]，进而从抗疲劳制造的角度对工艺参数进行择优。

能量法预测中低周疲劳寿命往往采用忽略加工表面特征或增加其他工艺来减小表面层影响的方式。通过疲劳试验来获得金属材料的疲劳强度要花费大量的时间和金钱，因此更多学者花费了大量的精力试图建立疲劳强度和基本力学性能之间的关系，例如，Wang 等[5]建立了拉伸性能确定疲劳强度的方法，庞建超[6]认为低强度范围的疲劳强度与抗拉强度呈线性关系。然后这些都是在保持相同加工硬化能力的前提下忽略了加工表面层特征。 Wu 等[7]和Wang 等[8]研究表明虽然加工表面层特征的改变对拉伸强度影响很小，然而对疲劳强度有很大的影响。Nalla 等[9]指出表面层的残余压应力显著降低了钛合金的循环软化速率，从而影响了低周疲劳循环行为影响。徐海丰[10]考虑到表面粗糙度以及机械加工在表面产生的残余应力影响钛合金的循环硬化/软化行为，采用轴向打磨和拋光处理的方式对试样进行处理，然而忽略了机械抛光产生的加工硬化也会影响到材料的循环行为。采用能量法研究材料整体力学性能，忽略机加工表面层特征似乎成为了一种很无奈的选择，且少有文献考虑加工表面完整的能量法疲劳寿命预测模型。因此，建立合适的考虑表面完整性的能量法预测模型，不仅能提高寿命预测精度，而且对面向服役性能的表面完整性参数评价具有重要意义。

本文通过引入加工表面完整性影响因子，定量描述表面几何-力学-组织特征参数对疲劳寿命的影响程度，并将该影响因子与能量法相结合，提出一种新的考虑加工表面完整性的疲劳寿命预测模 型[11]。 最后以重载车辆扭力轴高强度钢45CrNiMoVA 材料实际服役环境为背景，设计与实际扭力轴相同应力集中系数的扭转疲劳试样，通过对表面完整性参数测量和疲劳性能试验，揭示了正火态和淬火态45CrNiMoVA 高强度钢的机加工工艺对扭力轴材料疲劳循环行为的影响，验证了提出模型的有效性。

1 背应力能预测疲劳寿命分析

在不同应变幅控制下，将每个应变幅下最大稳态环的顶点连线定义为循环切应力-应变曲线，如图1 虚线所示。图1 中：Oγτ为以循环迟滞回线底点为原点的坐标系，O′γ′τ′为以循环切应力-应变曲线底点为原点的坐标系，循环切应力-应变曲线标度放大一倍，可得到循环迟滞回线上半枝，同理循环切应力-应变曲线原点对称标度放大一倍，可得到循环迟滞回线下半枝；A、B、C、D、E分别为循环迟滞回线顶点在Oγτ坐标系的τ轴坐标点、顶点、γ轴坐标点、循环迟滞回线上半枝与O′γ′τ′坐标系τ′轴交点、循环迟滞回线下半枝与O′γ′τ′坐标系τ′轴交点，O′为循环切应力-应变底点，γp、γe分别为循环切应力-应变曲线上任意点在O′γ′τ′坐标系上的塑性切应变值、弹性切应变，Δγp、Δγe分别为循环迟滞回线的塑性切应变幅、弹性切应变幅，ΔWp、 ΔWl分别为循环迟滞回线上下半枝围成的面积、下半枝与Oγτ坐标系γ轴围成的面积，Δτ为循环迟滞回线的应力幅。

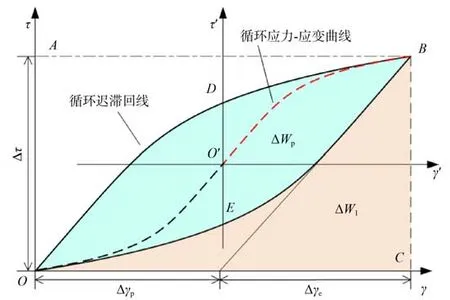
图1 循环迟滞回线曲线Fig. 1 Cyclic hysteresis loop curve

令γa为循环切应力-应变曲线上任意点在O′γ′τ′坐标系上的弹性切应变值，其表达为

式中：τa为剪切应力；G为剪切模量；k′为循环强度循环；n′为循环硬化系数。

循环迟滞回线(图1 中蓝色区域的上枝曲线和下枝曲线)反映了材料在疲劳断裂过程中的循环力学特征，通常采用循环应力-应变曲线来描述。当循环应力-应变曲线坐标标度放大一倍后，可以描述为循环迟滞回线的形状，若坐标原点取在迟滞回线环的底点(O点)，则仿照式(1)可将循环迟滞回线的上枝曲线为

即

每个循环塑性应变能密度ΔWp，定义为循环迟滞回线的上枝和下枝曲线所包围的面积，如图1 所示，即

进一步可变换为

故有

将坐标原点取在最小弹性段的滞后环下端点(见图1)，环ODBEO成为最小环。沿弹性段调整各环所得到的重合上枝ODB称为基本滞后环曲线。滞后环曲线由式(3)表达，将式(6)之积分写成弹性及塑性二部分之和：

联立式(3)、式(6)和式(7)，可得

得到

在研究金属材料的低周疲劳行为时，背应力X和摩擦应力τF是循环迟滞回线中两个重要的力学参数[12]。背应力与局部应变过程相关，提供了与移动位错的长程相互作用力，主要与材料中的微观结构屏障或应变不相容性[13]有关，摩擦应力通常对应于位错移动所需的局部应力，主要与材料中的短程障碍物有关，如晶格摩擦、沉淀粒子、外来原子等位错[14]。

对于循环迟滞回线，背应力能密度 ΔWb满足

式中：nb为循环背应力硬化系数。

根据能量法，在每个循环中，零件或部件由于吸收外部能量而在内部产生不可逆的损伤，并且一旦达到能量阈值，零件就会因疲劳而失效。考虑到弹性变形是可逆的，只有塑性应变才能引起不可逆的疲劳损伤，疲劳累积损伤模型为

式中：WfT′为累积循环应变能；Nf为疲劳寿命；Wf′和β为材料常数。

在实际应用中，往往采用稳定时的单周循环塑性背应力能密度ΔWb作为描述疲劳损伤的参量，它的物理意义为Wf′为ΔWb与疲劳寿命指数Nf-β的乘积：

2 表面完整性影响因子

对于零部件加工表面层与基体几何-力学-组织特征无差异的情况下，式(12)具有很好的适用性。然而在实际生产过程中，最后的机加工制造环节很难做到表面和次表面的无残余应力状态。较深的残余压应力层使得材料在一个周期内的塑性应变能密度ΔWp发生改变，尤其是经过表面强化后。同时由于表面层材料微观结构中位错的重排和密度的变化，使材料的总的塑性能发生了变化。图2 给出了表面层的残余应力能量修正系数：

式中：h0为残余应力降低为0 MPa 时层深；f(h)为残余应力随深度变化的拟合曲线，h为任意点的残余应力层深； cos ( 0.5πh h0)为考虑不同深度处的残余应力对疲劳寿命的权重系数。为适用于表面强化等方式引起的较深残余应力的表面层，图2(图中σres为残余应力，n为材料常数，ΔKth为考虑表面形貌和显微硬度的总能量修正系数)红色部分给出另一种残余应力修正系数：

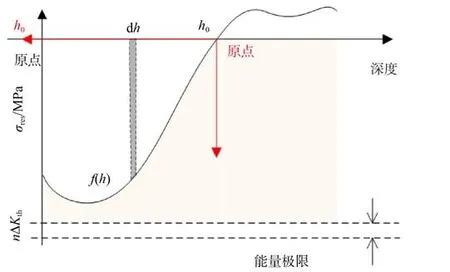
图2 残余应力引起的总应变能变化Fig. 2 Change of total strain energy caused by residual stress

表面较差的几何形貌势必使得疲劳断裂过早发生，总的应变能Wf′发生改变，如图2 所示。对于高强度钢而言，硬度较大时的高强度钢对微裂纹具有很强的敏感性，表面硬度大的区域反而成为较粗糙表面的致命疲劳源，具体为

式中：Hv为表面显微硬度；为表面微裂纹不扩展阈值[15]，具体为

a为表面形貌微裂纹深度方向特征参数，取值为表面轮廓算数平均偏差Ra，b为表面微裂纹水平间距特征参数，取值为表面轮廓微观不平度间距Rsm[16]。考虑到粗糙度轮廓具有随机分布特征，深度很大一部分低于表面轮廓最大高度Ry[17]，因此引入表面轮廓十点不平高Rz，且Ry/Rz能够很好地反映缺口几何特征[18]，因此式(16)中a的最终取值为RaRy/Rz。

通过将几何-力学-组织的多特征修正项代入能量法预测模型中，得到的修正模型如下：

式中：m为材料的固有系数。

3 试验安排

3.1 试样制备

试验材料选用重载车辆扭力轴高强度钢45CrNiMoVA材料，正火态钢的抗拉强度和屈服强度分别为892 MPa、521 MPa，淬火态钢的抗拉强度和屈服强度分别高达2 004 MPa、1 652 MPa。结合重载车辆扭力轴实际服役环境，试验安排如图3所示。扭力轴遇到爬坡时，负重轮向上抬起，扭力轴受到来自平衡肘的剪切扭转作用，长时间的循环扭转使得扭力轴容易在圆弧段和直线段的过渡区发生扭转疲劳断裂。为使疲劳试样更加符合实际服役环境，试样圆弧段采用相同的应力集中系数进行设计，等比例关系R/D=r/d，其中r、d分别为扭力轴过渡圆弧半径尺寸、扭力轴中间直径尺寸，R、D分别为小试样过渡圆弧半径尺寸、小试样中间直径尺寸。文献[19]给出了直径52 mm的重载车辆扭力轴的圆弧半径为100 mm，可得试样直径D=12.5 mm时对应的圆弧半径R=24 mm，试样设计基于国家标准GB/T 12443—2017金属材料 扭矩控制疲劳试验方法，设计的试样符合实际扭力轴实心服役条件。

图3 试验安排Fig. 3 Test arrangement

图3 中的加工切削参数如表1 所示。使用基恩士公司生产的VK-X100 型3D 激光扫描显微镜测量表面形貌和粗糙度，通过多次测量取平均值的方式获得表面粗糙度。采用南京山特仪器有限公司生产的HXS-1000A 型显微硬度计(南京山特仪器有限公司生产)对试样表面显微硬度进行测量，采用爱斯特公司生产的X-350A 型X 射线应力分析仪通过电解层去除法在两个正交方向(周向和轴向)上测试残余应力，残余应力测试仪(邯郸市爱斯特应力技术有限公司生产)使用常规X 射线衍射法，利用sin2ψ公式，侧倾固定ψ法。考虑到机加工产生较小的表面层，测试层间距约为3 μm。

表1 正火态45CrNiMoVA 钢加工工艺安排Table 1 Machining of normalized 45CrNiMoVA steel

在微机控制的MTS-250kN809 闭环伺服液压试验机(美国美特斯公司生产)上进行纯扭转疲劳测试，考虑到扭力轴服役中受到单向扭转，应变比为0、室温环境下正弦波全应变控制方式、最大应变为 0.013 mm/mm，用美国伊普西龙公司生产的Epsilon 周向扭转引伸计测量单调扭转试验中的 应变。

3.2 背应力能分析

如图4 所示，单周次的循环塑性应变能中主要包含摩擦应力τF做功和背应力X做功。其中，摩擦应力τF做功以热能形式扩散出去，背应力X做功产生的位错塞积能等特征能够更好地反映疲劳性能。

模型的物理意义如图4 所示，当摩擦应力τF在参考文献[20-21]中建议的1.0×10-5反向塑性应变偏移量确定以后，背应力X满足

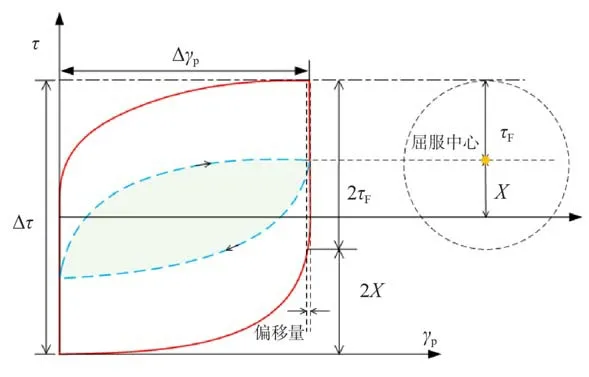
图4 循环迟滞回线中的背应力和摩擦应力Fig.4 Back stress and friction stress in hysteresis loop

结合式(9)，可得

图5 所示为不同表面层对背应力和摩擦应力影 响趋势。从图5(a)中可以看出，随着循环周次N的变化，不同表面层的背应力X具有相同的变化趋势，均呈现先循环硬化后软化，但磨削工艺表面层产生了更大的Xmax，精车湿切工艺表面层产生了最小的Xmax，同时磨削工艺表面层产生了最大的摩擦应力τF且逐渐趋于稳定(见图5(c))，3种车削工艺产生的摩擦应力并未发生明显的变化。

图5 不同表面层的背应力和摩擦应力分析Fig. 5 Analysis of back stress and friction stress in different processes

通过式(19)得到的不同表面层的循环背应力能变化趋势如图6 所示。由图6 可知，不同加工工艺表面层对循环背应力能的变化趋势产生了不同影响，磨削工艺相对3 种车削工艺具有最小的背应力能密度，且随着循环周次的增加，具有稳定的背应力能密度(0.827 9 MPa·mm/mm)，在后期的寿命预测过程中以稳定态的背应力能作为计算量。然而半精车(湿切)和粗车具有更大的循环背应变能密度，且呈现一直增大的趋势，最后发生断裂。

图6 不同加工表面层的背应力能密度随循环周次的 变化趋势Fig.6 Variation of cyclic back stress energy with life in different processes

3.3 加工工艺对表面完整性的影响

加工表面完整性特征参数和扭转疲劳寿命如表2 所示。考虑到不同深度的残余应力测量完成后难以进行后续扭转疲劳测试，首先取4 根不同加工工艺表面层的残余应力随深度分布曲线，考虑到试样的断裂形式为剪断，对周向残余应力进行测量，结果如图7 所示。首先对测试的残余应力点进行多项式拟合，通过式(13)可得因残余应力引起的不同加工工艺的能量修正值，分别为1.356 MPa·μm、2.76 MPa·μm、2.63 MPa·μm、 -1.538 MPa·μm，疲劳测试试样的表面残余应力能修正项为

图7 不同表面层的残余应力随深度的变化趋势 Fig. 7 Variation of residual stress with depth in different processes

表2 正火态45CrNiMoVA 钢的加工表面完整性与扭转疲劳寿命表征Table 2 Characterization of machined surface integrity and torsional fatigue life of normalized 45CrNiMoVA steel

式中：σsurf表示疲劳测试试样的表面残余应力；σsurf,conf表示残余应力测试试样的表面残余应力；Wre′s,conf为残余应力测试试样的能量修正项。考虑到表面层残余应力、层深、权重系数三者的变化，比例能量修正项取，图8 给出了寿命随循环能修正系数的变化趋势。

图8 寿命随循环能修正系数的变化趋势Fig. 8 Variation of life with correction coefficient of cyclic strain energy

如图9 所示，在循环应变能法预测寿命时，不考虑机加工表面完整性的影响，单周次循环应变能密度为常数，扭转疲劳寿命预测误差带为2.02 倍。当考虑加工表面完整性对扭转疲劳寿命的影响时，寿命预测误差分散带显著降低，为1.25 倍，且平均预测精度从72%显著提高为0.9%。同时，为验证模型的可行性，对疲劳试验后的不同试样的单周次能量密度进行计算，并预测扭转疲劳寿命。结果表明：疲劳试验前考虑表面完整性的模型与通过疲劳试验后计算单周次循环背应力能密度预测模型的误差分散带相同，均为1.25 倍，表明本文建立的考虑表面完整性模型具有很大优势，可以实现疲劳试验后的实时统计循环背应力能密度的繁琐计算过程和和疲劳试验。

图9 正火态钢考虑表面完整性的模型预测精度Fig. 9 Model prediction considering surface integrity of normalized steel

在考虑加工表面完整性的能量法预测模型中，最终得到的修正模型式(17)中，考虑残余应力修正系数的材料常数m与考虑表面形貌和硬度的修正材料常数n呈现7.38 倍线性关系，这就提供了一种新的表面完整性定量评价方法，可以通过获得一定的残余应力能量修正系数的方式的来弥补实际机械加工生产过程中难以避免的缺陷。

同时对高强度钢车磨削工艺的扭转疲劳寿命预测验证，加工表面完整性与扭转疲劳寿命表征如表3 所示，加工工艺如表4所示，总加工余量为0.6 mm，试样详细尺寸如图3 所示，疲劳试验过程中，应变比为0，最大扭转应变为0.0154 mm/mm。

表3 淬火态45CrNiMoVA 钢的加工表面完整性与扭转疲劳寿命表征Table 3 Characterization of machined surface integrity and torsional fatigue life of quenched 45CrNiMoVA steel

表4 淬火态45CrNiMoVA 钢加工工艺安排Table 4 Machining of quenched 45CrNiMoVA steel

图10 给出了疲劳试验后通过计算不同试样的单周次循环背应力能密度的扭转疲劳寿命预测结果，预测精度从72.7%降低到了30.3%，误差分散带(蓝色虚线)从1.82 倍扩大到了3.30%，不考虑加工表面完整性预测疲劳寿命具有较大的预测误差，严重阻碍了循环应变能法预测不同表面状态下的扭转疲劳寿命。考虑加工表面完整性的疲劳前循环背应力能密度预测扭转疲劳寿命与不考虑加工表面完整性的疲劳后循环背应力能密度预测扭转寿命预测相比，平均预测精度提高到了92.2%，且误差分散带从3.30 倍降到了1.25 倍，显著提高了扭转疲劳寿命预测精度。该模型使得能量法适用于不同加工表面特征，且可以基于现有的试验数据准确预测尚未开展疲劳试验的中低周疲劳寿命。

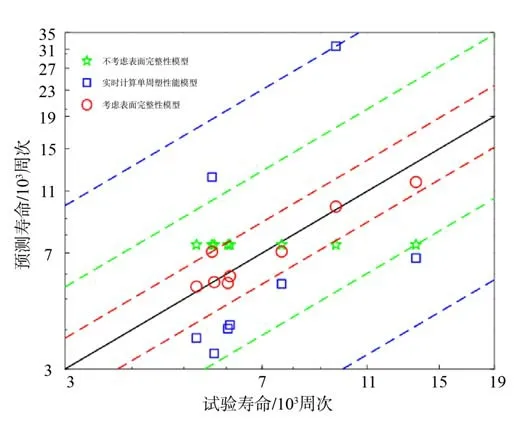
图10 淬火态钢考虑加工表面完整性的能量法预测 精度Fig. 10 Model prediction considering surface integrity of quenched steel

4 结论

本文针对传统循环应变能法预测疲劳寿命忽略了加工表面层特征，提出了一种考虑高强度钢加工表面完整性的背应力能法疲劳寿命预测模型，并以重载车辆扭力轴高强度钢材料实际服役环境为背景，设计与实际扭力轴相同应力集中系数的扭转疲劳试样，验证了模型的可行性。得出主要结论 如下：

1)本文引入了一种考虑加工表面完整性的修正因子，该修正因子能够较好地描述不同表面完整性参数对疲劳性能的影响程度。残余应力能修正项Wre′s不仅考虑了表面残余应力的影响，同时考虑了不同深度处的残余应力对寿命的影响。硬度和粗糙度修正因子ΔKth考虑了表面形貌高度特征RaRy/Rz参数，将水平宽度特征Rsm参数引入修正因子中，同时考虑了表面微裂纹对硬度的敏感性，与试验疲劳寿命具有很强的一致性。

2)本文针对重载车辆扭力轴实际服役工况，通过扭转疲劳试验验证了考虑表面完整性的修正模型的有效性，相对不考虑表面完整性的所有数据的误差分散带缩小了22%，预测精度提高了25%；相对实时统计单周次能量密度的寿命预测，预测平均精度提高到了92.2%，且误差分散带从3.30 倍降到了1.25 倍。

3)本文提出的模型克服了因实时计算不同表面完整性引起的单周次应变能的繁琐工作以及不适用性，可以基于现有的试验数据准确预测尚未开展疲劳试验的中低周疲劳寿命，通过添加表面完整性的修正因子，实现了面向服役性能的残余应力与表面形貌和显微硬度的疲劳寿命预测，同时提供了一种新的表面完整性定量评价方法，为面向疲劳服役性能的主动控制提供了依据。