基于泛函分析法的引信自毁时间散布
2023-04-02赵新纪永祥刘刚刘社锋罗熙斌宁小磊
赵新, 纪永祥, 刘刚, 刘社锋, 罗熙斌, 宁小磊
(中国华阴兵器试验中心,陕西 华阴 714200)
0 引言
引信作为弹药的重要组成部分,作用是引爆战斗部,使弹药完成预定任务。但当弹药发射后未命中目标时,就会落在非攻击区,已处于待发状态的引信可能会引爆战斗部危及攻击范围外人员和设备的安全。因此,要求引信在任务范围外不发火,此不发火范围外称为非攻击范围。通常引信在任务范围内的弹道发火,使战斗部炸毁,以防止对安全范围内人员及设备的危害。为达到炸毁的目的,引信中都设置了使战斗部自炸的机构,称为自毁机构。自毁机构作为引信安全系统的重要组成部分,它控制的时间精度关系到引信能否对己方人员和设备提供安全保障,主要包括自毁时间的最小值和最大值,最小值应大于最大攻击距离及发射载体的安全距离,最大值应小于安全范围以确保人员和设备的安全[1]。在自毁机构中离心自毁机构广泛应用于高转速弹药中,其通过外弹道飞行中离心力衰减来控制自毁时间,易受到弹丸飞行环境的影响,导致最小值和最大值的不确定,造成不同条件下离心自毁时间不准确,无法掌握引信自毁特性。文献[2]通过大量的样本搜集,获取了自毁时间数据,统计获取离心自毁引信自毁时间的分布。文献[3]根据离心自毁机构的理论计算公式调整自毁时间,达到满足对战术技术指标的理论设计,都达到了掌握自毁时间的目的。在性能鉴定试验中无法进行大样本量的引信自毁时间试验,而单次试验易受外部环境的影响而改变理论自毁时间,简单的通过试验结果回答战术技术指标,会对部队使用训练造成一定的安全隐患。
本文对性能鉴定试验中样本量小的情况,提出了应用泛函分析法[4-5]对引信离心自毁机构进行建模,通过分析弹丸弹道飞行模型[6-7],建立初速和自毁转速对应时间关系,将初速分布和自毁转速分布应用到时间关系模型中,求解相关分布参数,获取时间散布区间,为引信自毁时间试验提供理论支撑,为部队训练使用提供技术指导,为研制方参数设计提供数据依据。
1 自毁模型建立
在建立引信自毁时间模型时,首先需要了解引信出炮口后运动情况和相关参数值,达到引信自毁机构的自毁时间理论值,来建立含有偏差参数的模型[8-9]。
1.1 引信自毁时间理论模型
钢珠在膛内所受的离心力是逐渐增大的,后坐力则很快到达最大值,然后逐渐下降。切线惯性力的变化规律同后坐力,但量值上小得多,其作用只是引起摩擦。因此可以认为只要在最大膛压后钢珠一旦锁住击发体,便将一直锁住到离心力减小、转速下降至自炸。图1 所示为自毁钢柱受力情况。 图1 中,C为钢珠所受离心力,F为环面反力;p2为锥面反力,p为自炸簧抗力,φ为摩擦角,α为锥面与水平面夹角,ωT为理论自毁转速,i为钢珠数目,r为弹轴至钢珠中心的距离,O为钢珠中心,B为自炸簧抗力延珠心方向与接触点E在水平方向的交点,H为p转动φ后与BE交点,E为钢珠与斜面接触点。
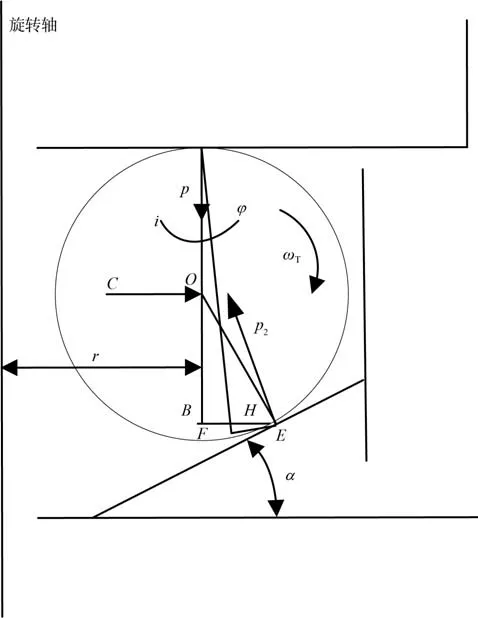
图1 自毁钢珠受力情况Fig. 1 Forces on the self-destroying steel ball
忽略科氏力的作用及钢珠的转动,可以得到引信自毁时理论转速[10],即
式中:g为重力加速度;d为钢珠直径;γ为钢珠材料的比重。
在理论自毁时间转速求解过程中,理论转速ωT服从正态分布,有ωT~N(μ1,σ12),μ1为理论转速ωT的均值,,σ1为理论转速ωT的方差。在解算时,实际自毁时间对应的自毁转速ωTure由理论转速ωT和随机误差转速ωr组成,ωr服从正态分布N(μ2,σ22),μ2为随机误差转速ωr的均值,σ2为随机误差转速ωr的方差,即
由于ωT和ωr服从相互独立的正态分布,将ωT、ωr对应正态分布代入式(2)中,则ωTure的表达式为
1.2 弹道模型
弹丸在膛内受火药气体的作用,产生速度和受缠度影响的转速等。出炮口时,内弹道受力模型发生改变,使弹丸形成外弹道飞行模型,通过对弹丸在外弹道飞行情况分析,且假定地表面为平面、重力为常数,建立弹丸外弹道模型[11-13]如下:
式中:ux、uy和uz分别为x轴、y轴和z轴方向的速度分量;x、y、z分别为距离、方向和高程;ρ为空气密度,
R1为气体常数29.27,τ0为地面标准虚温288.9 K,G为拟合系数6.328×10-3K/m2;S为弹丸参考面积;m为弹丸质量;FD为阻力符合系数;CD0为阻力系数;u为弹丸运动速度;g0为当地重力加速度; Jx为x轴向转动惯量;ω为弹丸转速;d1为弹径;Clp为滚动阻尼力矩系数; ℎ(y)为气压;τ(y)为虚温。
设μ3为理论初速的均值,σ3为理论初速的方差,u0为出炮口时初速,服从正态分布,则有。
当初值t=0 s时:
式中:θ0为射角;L0为身管长度;y0为初始高度;ω0为初始转动角速度;η为膛线缠度;ℎ0为地面气压。
1.3 数学模型建立
将式(7)表示为积分形式,即
式中:T为弹丸飞行时间。
将式(6)条件代入,则式(8)表示为
式(9)中ω与式(3)中ωTure相等时,引信发生自 毁,则
式(10)为初速与自毁转速关于时间的关 系式。
1.4 泛函分析法
泛函分析是一种广义的函数分析方法,它主要研究空间、算子之间的关系,建立普遍性的规律,以某类未知函数抽象积分型函数来解决极值 问题[14-15]。
将式(10)表示为泛函形式,则
式中:x′、y′、z′分别为x、y、z的1 阶导数。 求V的1 阶变分:
利用分部积分,可得
由1 阶变分等于0,式(13)可得到3 个微分方程,即
通过对式(10)中变量求解微分,得到如下方程:
将式(15)代入式(14),则
将式(3)、式(4)、式(10)和式(16)联立,获得初速u0、自毁转速ωTure和自毁时间t的关系。
2 仿真实验
将基本参数d=23 mm,m=188.5 g,v=1 020 m/s,η=30 ,c43=1.893 ,i43=1.33 ,p=27.5 N ,r=7.75×103kg/m3,钢珠直径dq=2.38 mm,i=5,摩擦力fa=0.15,G=6.328×10-3K/m,τ0=288.9 K,g0=9.8 m/s2,Clp=-0.0102,CD0=270,h0=750 mmHg,FD=1.0107 代入第1 节的自毁时间数学模型中,进行仿真实验分析。
2.1 试验情况
在某高低温试验时,使用新身管和旧身管分别进行自毁时间试验,试验获得初速、温度和自毁时间的试验数据,如表1 和表2 所示。
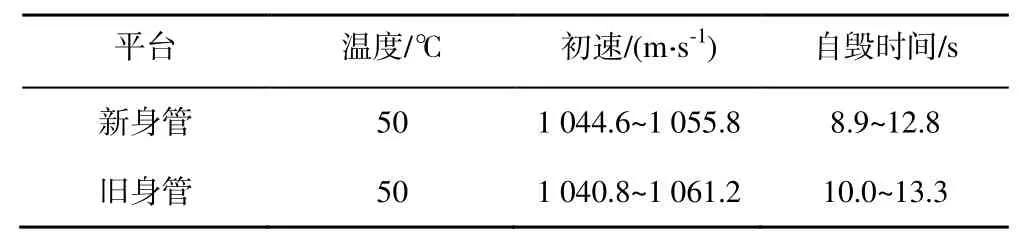
表1 高温引信自毁情况Table 1 Self-destruction time of the high-temperature fuze

表2 低温引信自毁情况Table 2 Self-destruction time of the low-temperature fuze
2.2 数据处理
根据表1 和表2 中不同射击平台的初速及自毁时间试验数据,求解获得自毁转速数据,如表3 所示。将表3 中同温度不同平台的均值和标准差进显著性水平 =0.05α的假设检验,可以得到检验结果,如表4 所示。
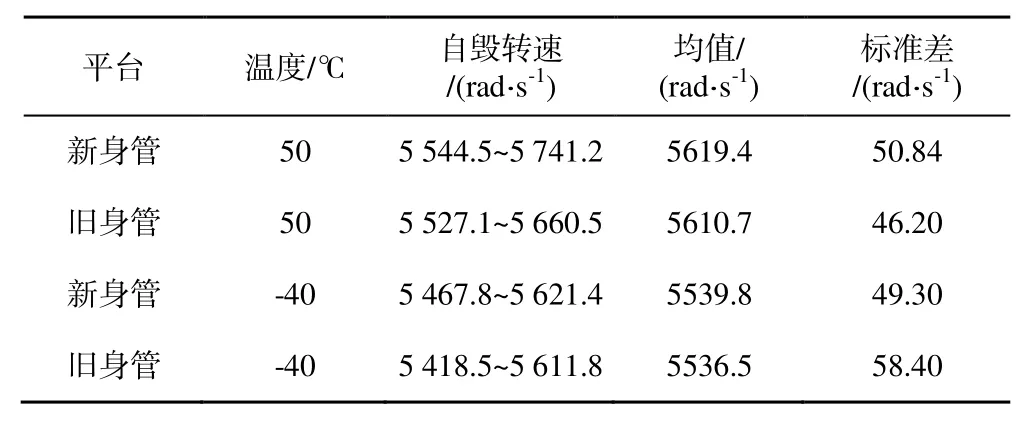
表3 自毁转速计算结果Table 3 Calculation results of self-destruction rotating velocity
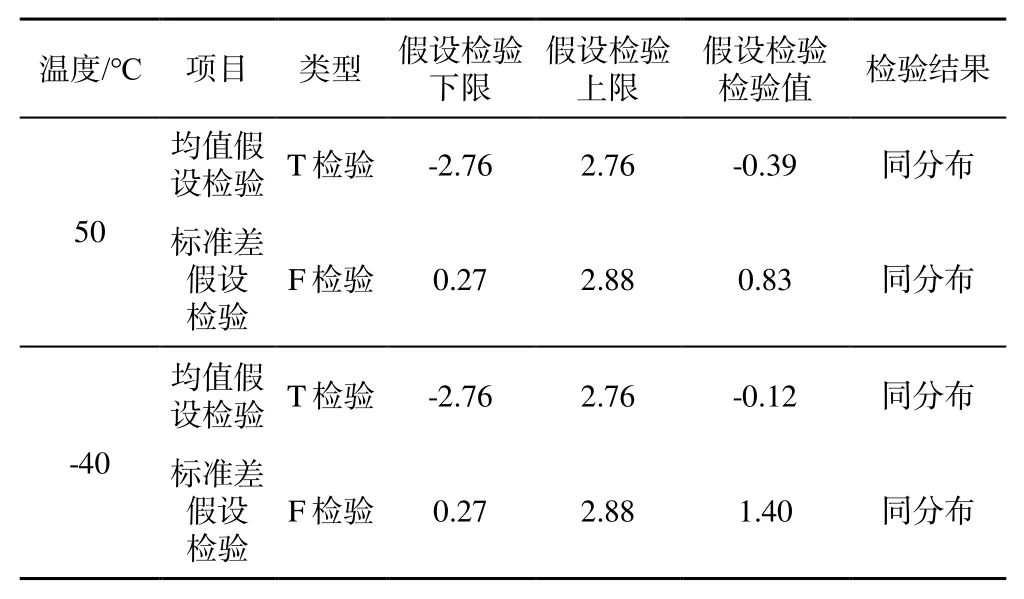
表4 假设检验结果Table 4 Hypothesis test results
通过假设检验可知,本文方法在解算自毁转速时是可行的,不因发射平台发生改变而产生不同分布。
2.3 引信自毁时间散布
通过2.2 节数据处理,可以获取自毁转速,并通过假设检验可知两次试验结果同分布,则对本文提出的解算自毁时间模型进行了检验,证明了模型和自毁转速计算的正确性。假设战术技术指标要求3.5~15.0 s 自毁率分别满足双边90%、双边95% 两种情况,将指标要求的自毁率代入自毁时间散布中,可以得到自毁率散布区间如表5 所示。
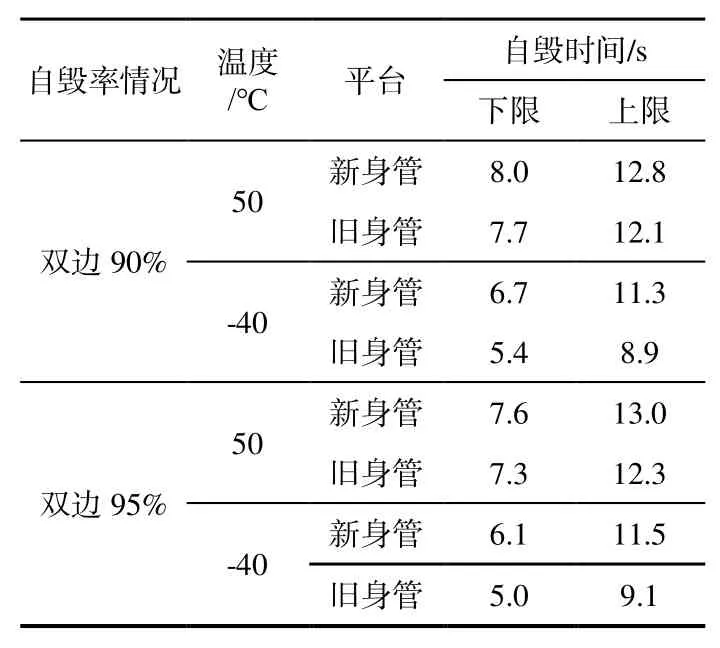
表5 自毁率散布区间Table 5 Self-destruction rate distribution interval
2.4 结果分析
表1 给出了不同寿命的身管射击高、低温弹丸的自毁时间,通过本文提出的方法计算出各自的自毁转速,再通过假设检验,验证了本文提出方法的可行性,能够用来计算自毁时间散布。表5 给出了双边90%、双边95%的自毁时间值,分析得到:
1)弹丸自毁时间分布均偏向自毁时间下限;
2)随着弹丸温度的降低,自毁时间向下限 靠近;
3)随着身管的使用,自毁时间下限靠近极限自毁时间;
4)双边95%时自毁时间比双边90%更接近自毁时间极限,为考核提出更严格的要求。
通过本文提出的散布区间分析方法,能够有效地判断自毁时间散布区间,确保了引信自毁时间试验小样本量情况下的可靠性和有效性,根据分析可以发现:在新身管和高温环境时存在自毁时间偏长的现象,对弹丸飞行方向攻击区域外有安全隐患;在长时间使用后的身管和低温环境存在自毁时间偏短的现象,对发射平台附近的己方人员的防护和安全提出了警示。
3 结论
本文针对性能鉴定试验中自毁时间试验样本量小造成结果可信度低的现象,提出利用泛函分析法对初速与自毁转速的联合分布模型求解引信自毁时间散布区间。通过设计中理论转速和随机误差转速组成的真实自毁时间对应自毁转速与弹道方程,建立泛函分析模型,再利用欧拉-拉格朗日方程对泛函分析模型求解,获得自毁时间模型,再求解自毁时间散布区间。得到主要结论如下:
1)本文方法通过假设检验判断了方法的可行性,并通过不同温度的样本量求解散布区间,散布区间在旧身管射击低温弹丸时偏向自毁指标下限。
2)在身管寿命减小的情况下,自毁时间靠近下限,可能在部队使用中带来安全隐患,对部队身管使用寿命提供了自毁时间判断方法。将其运用到战术技术指标考核中,通过小样本试验反映出真实的引信自毁时间区间,为回答指标提供数据参考。
3)将其应用在研制方引信自毁时间设计过程中,为设计中调整引信自毁时间参数提供依据。
4)在部队训练使用时,可通过自毁时间散布对作战人员和装备的安全隐患提供理论支撑。
