基于DAS的光声断层图像重建算法研究

张瑛，王浩全，李子圣，王小婷，李凯丰，侯清

（中北大学 信息与通信工程学院，山西太原，030051）

0 引言

近年来，医学成像领域有了很大的进步。光学成像的优点是对比度很高，但是空间分辨率比较低，成像深度受到光传播深度的限制；超声成像虽然能获得生物组织一定深度的高分辨率图像，但是图像的对比度比较低。光声层析成像(Photoacoustic Tomography, PAT)能够结合光学成像和超声成像的优点[1～3]，逐渐成了医学成像方面的研究热点之一。

光声断层成像的重要步骤是图像重建，常用的重建方案是利用组织边界处记录的压力信息来获得初始压力分布。1995年，Krugger等人首次将光声应用到生物组织成像领域[4]，在后来的时间中，国内外很多研究小组都开始将目光聚焦到光声成像领域。在国外，研究光声成像的小组有，(1)华盛顿大学的汪立宏教授小组，汪教授小组在光声断层成像方面做了很多研究[5]。(2)伦敦大学学院的Beard, Paul实验组，该小组专注于研究生物医学光谱成像，提出用一个基于高分子薄膜的Fabry-Perot干涉仪的光学检测光声信号的成像系统[6]。在国内，研究光声成像的小组有复旦大学汪源源教授团队和华南师范大学邢达教授团队，他们在光声成像系统开发以及光声图像重建等方面做了很多研究[7]。除此之外，厦门大学等许多所高校也在从事光声成像技术的研究，并且取得了优秀的科研成果[8～10]。

在光声图像重建实际应用中，针对图像重建需要快速处理等问题，本文采用延迟求和（DAS）算法，对图像进行实时重建。

1 光声断层成像原理

PAT中的正向问题涉及收集给定初始压力分布情况下，组织边界上的压力数据。声波在生物组织中的传播可以使用波动方程建模，如式(1)所示：

式中，c是介质中的声速，β是热膨胀系数，pC是比热， (,)Hdt是单位时间内单位体积的吸收能量，空间位置由d表示。对于固定声源，吸收能量可以写成在应力约束条件下，光源的时间部分可用δ函数表示为式(1)中的相当于解决式(2)的初值问题[11]：

超声换能器在位置0r处所探测的声压信号也即光声信号作为公式(2)的解，表示为：

公式(3)表明，位置r时刻r的光声信号是沿着半径为ct的球面积分的初始声压分布的时间导数。不同的重建算法其实就是利用换能器探测到的通过不同方法去计算成像组织的初始声压分布

2 基于延迟求和的光声图像重建算法

当激发激光脉冲的持续时间短到足以满足声学和热约束条件时，由于光激发而发射的压力场随空间r和时间t的变化可以表示为：

其中 ()′Hr是组织中每单位体积的吸收能量，Γ是无量纲Grüneisen参数，c是声速。在下文中省略了常数项因为它不影响基于模型的重建。沿半径为的球面S(r,t)进行积分。式(4)中正向模型的离散化是通过考虑笛卡尔网格上的N个体素来完成的，表示包围所有光声源的体积。每个图像体素的位置由ri表示。空间H(r′)中任意位置处的吸收能量近似为插值函数K(r′)的加权叠加移动到不同的体素位置ri，即：

其中ih是体素i处的吸收。那么，式(4)可以表示为：

通过定义：

由式(3)，得：

Δ是体素大小，r=(x,y,z)。插值函数的非零值仅存在于体素i的邻域，即当r′距离体素i小于一个体素时，hi仅影响H(r′)。因此，式(8)中的曲面积分仅为当曲面与曲面相交时的Δ邻域，如图1所示。让测量位置r和体素位置ir之间的距离用s表示。因为体素大小Δ通常比s小几个数量级，s中的球面积分，ir体素的邻域可以通过平面积分来近似。在从ir到 ′r的方向上，积分值取决于距其表面d（用S′表示）到体素ir的距离，可以用参数化两个角度α和β。因此，当ct=s-d时式(6)可以重新表述为：

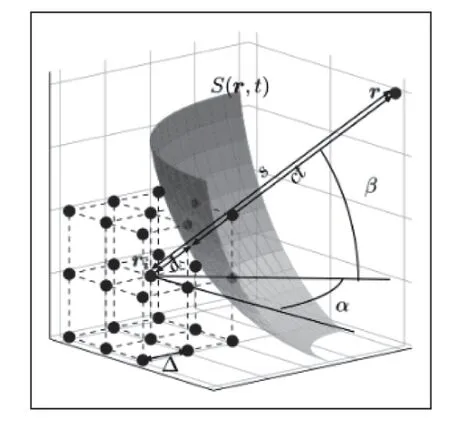
图1

图1 笛卡尔网格上光声正演模型的三维离散化。球面积分面S（r，t）与体素i的∆-邻域的交点。体素i和测量位置分别用ir和r表示。ir和r之间的距离用s表示，ir和球面之间的距离由d表示。方位角和仰角分别用α和β表示。

其中A是表示特定重建问题的模型矩阵。A的列表示与网格的每个体素相关的光声信号。重建问题包括嵌入吸收矢量x，对于该矢量，理论模型与实验测量的压力信号b更好地匹配。

延迟求和算法有两种遍历方式：基于传感器的遍历和基于重建像素的遍历。基于传感器的遍历方法是基于传感器来计算传感器在重建图像上的每个时刻的信号区域，根据传感器的空间响应范围，将强度叠加在重建区域上。基于重构像素点的遍历是根据像素点计算与每个传感器的相位角，看是否在传感器的空间接收范围内。如果在范围内，计算与传感器的距离、计算延时以及相应的强度。最后，对每个范围内的传感器强度进行累加，得到像素的最终光吸收强度。

延迟求和法是通过式(11)来反演组织内的光吸收分区情况：

本文采用的算法根据探测器与生物组织实验点之间的距离，计算超声传输到探测器的延迟，最终确定生物组织发射光波时声源的强度，并将每个探测点处的波束形成信号求和。在延迟求和这一算法中，主要使用超声换能器检测实验样本和生物组织的声压信号，根据传感器位置与需要重建生物组织位置之间的距离差，使生物组织某一点吸收的光量被反转。

本文实验采用线性阵列探测器，如图2所示。假设光声信号由线性阵列探测器检测，波束形成信号和DAS的接收信号之间的关系可以定义为：

式中，SDAS(x,y)是探测点(x,y)处的波束形成信号，S(i,τ)是时间t处第i个探测器元件的接收信号。延迟时间t(x,y,i)表示在探测点(x,y)处产生的声波传播到第i个探测器元件的时间，它可以表示为：

式中，l(x,y,i)是探测点(x,y)和第i个探测器元件之间的距离，c是声速。该算法通过选取适当的数据点的平均值形成图像像素后，可以使用式(11)获得重建图像。除像素点(x,y)外，与 PA 源（图 2 中的S(x,y)）具有相同距离的所有像素都将受到强信号的影响。由于有效信号与不必要的数据相加，因此，在重建图像中不可避免地会出现旁瓣和伪影。

图2 信号波束形成图

由图2表示，位置（x，y）处的波束形成信号与第i个探测器元件接收信号之间的关系。旁瓣标记在PA源S的两侧。

本文的延迟求和算法采用的基于像素的遍历方法，其伪代码如下：

输入：传感器信号pn(t)，其中t代表时刻，n代表传感器序号；N为传感器个数；初始延迟t；声速c：传感器位置;权重ω= 1;nx,ny输出图像横纵坐标范围；传感器空间响应范围thea。

输出：组织分布图像A(r)，其中r代表像素位置。

计算：

延迟求和流程图如图3 所示。

图3 延迟求和流程图

3 实验结果与分析

本文对光声成像的成像环境进行了空间特征仿真，设置相关参数以便进行光声数据采集：设置成像网格为256×256pixels，分辨率为150μm；设置设声速为1540 m/s，声衰减为0.5 dB/MHz/cm，Grüneisen为0.15；设置的线性阵列是由128个间距为200微米的探测器组成，将这一阵列放置在固定平面，探测器中心频率为5MHz。

将光声数据采集信号应用于真值图像计算。在光声数据采集信号中加入高斯白噪声，来模拟实际环境。之后采用80%带宽脉冲响应函数（IRF）对每个采集到的光声信号进行滤波。

以上仿真采用的仿真软件为Matlab R2019a，在处理器 为Inter(R)Core(TM)i5-4210H、CPU@2.90GHz、内 存8GB的个人计算机上进行的。

图4(a)为原始模型图A（像素191×191），内有一个小男孩在图片右侧站着，手拿灯笼。图4(b)为所有探测器探测到的模型图A的声压信号。

图4 原始模型图A

图5是模型图A基于DAS的重建效果，可以看出，图像锐化了重建边缘，轮廓清晰，能够清楚地看到“小男孩手拿灯笼”这一景象，重建效果良好。

图5 基于DAS的重建结果

图6 (a)为原始模型图B（像素256×256），内为散放的大米。图6(b)为所有探测器探测到的模型图B的声压信号。

图6 原始模型图B

图7是模型图B基于DAS的重建效果，可以看出，重建图像效果没有较上一组（模型图A）重建效果好，存在相邻微观结构之间的混叠问题。这是由于来自一个目标的信号可能会受到来自相邻目标信号的影响，从而导致图像失真和混叠，并恶化图像质量。这是由于在图像信息过多时，使用DAS算法重建图像通常会出现高旁瓣和强烈伪影[12～13]。

图7 基于DAS的重建结果

4 结论

通过上述实验结果可以说明，DAS基于对波束形成信号的简单延迟和求和计算，能够快速响应，非常适合实时光声断层成像。然而，当图像信息过多时，在重建过程中有可能使用了一些不必要的数据进行求和，会使得基于DAS的光声断层图像重建结果有可能出现高旁瓣和强烈伪影。解决高旁瓣和强烈伪影这一问题，是DAS算法接下来的一个研究方向。