面向基准约束与余量约束的配准算法
2023-03-31朱燏肖世宏陈志同
朱燏,肖世宏,陈志同
(1.中国航空制造技术研究院,北京 100024;2.复杂构件数控加工工艺及装备北京市重点实验室,北京 100024;3.数字化制造技术航空科技重点实验室,北京 100024;4.北京航空航天大学 机械工程及自动化学院,北京 100191)
飞机的襟翼滑轨是一类重要零件,其加工工序繁杂、具有较大的尺寸与质量,其导轨面与基准之间必须保持相应的位置关系。精加工前零件的基准面已加工到位、导轨面已完成粗加工,因此,该零件在数控精加工前必须经过反复地找正,并根据零件的状态进行加工坐标系的调整[1]。
通过配准的方式来提高零件的找正效率、分配合适的加工余量是几何自适应加工技术的一个重要研究内容。在配准算法方面,主要算法有迭代最近点(iterative closest point, ICP)算法、鲁棒点匹配(robust point matching, RPM)算法、核相关(kernel correlation, KC)算法、混合高斯模型(Gaussian mixture models, GMM)算法等[2],用于解决点集之间的配准问题。其中ICP 算法是一种较为有效且快速的算法,在ICP 算法的基础上,Zhu 等[3]、Béarée 等[4]、Shi等[5]、Bergström 等[6]分别提出不同的方法对ICP 算法的计算效率进行提升,Zhou 等[7]、Du 等[8]针对ICP 算法进行了改善,可解决带有噪声的数据点的匹配问题。传统的ICP 算法是一类在全局坐标系下计算旋转矩阵与平移矢量的配准算法。
在应用相关配准算法时,需要根据工程背景增加相应的约束[9-10]。为了将配准算法与数控加工的应用相结合,冯亚洲等[11]提出基于公差约束的配准优化算法,Chen 等[12]提出测量点向偏置面的配准算法。此外,相关的配准算法还可以用于机器人加工[13]、航空零部件的检测[14]、零件修复[15]、整体叶盘的自适应铣削[16]、整体叶盘的自适应磨削[17]等多个与数字化制造相关的方向。
配准技术通常用在零件的精加工工序中。在绝大多数的航空零部件的实际加工过程中,精加工前的零件并不是毛坯状态。在绝大多数情况下,零件待加工面的配准结果必须保证待加工面与基准面或基准孔的相对位置关系,从而确保某些关键的形位尺寸。这种情况下的配准就需要保证几何体的变换方式是沿某个特定方向的平移或绕某个特定轴的旋转,并且配准后的结果需要保证待加工面余量的波动较小。这就需要根据特定的矢量或平面建立局部坐标系进行旋转平移变换,并将结果反算至全局坐标系中。本文即针对复杂零件的数控精加工过程,提出面向基准约束与余量约束的配准算法,开发相应的软件模块,用于实现零件精加工中的自适应调整。
1 余量约束配准与运动变换关系
1.1 面向余量约束的配准算法
为了建立数学模型描述带余量约束的配准问题,首先定义2 种距离,绝对距离与有向距离。检测点pi到理论点qi之间的绝对距离di如式(1)所示,该距离为绝对坐标系下2 点之间的范数:


1.2 局部坐标系与全局坐标系下的旋转、平移变换之间的数学关系
本文所提基于基准约束的配准算法最大的特点是不在全局坐标系(OWCSxyz)内进行配准,而是通过坐标系的转换,将点转换至局部坐标系(Oe1e2e3)下,再进行配准,最后,根据局部坐标系与全局坐标系之间的关系计算出对应的全局坐标系下的旋转矩阵R 与平移矢量T。因此,必须建立全局坐标系下的旋转矩阵 RWCS、平移矢量 TWCS与局部坐标系下的旋转矩阵 RLCS、平移矢量 TLCS之间的关系。
如图1 所示,全局坐标系下局部坐标系的3 个方向矢量为e1、e2、e3,坐标系原点为O,令矩阵M=[e1e2e3],任意一点P 在局部坐标系内为 PLCS,在全局坐标系内为 PWCS。在局部坐标系内经过运动的点在全局坐标系内的位置如式(5)所示,而在全局坐标系内经过运动的点的位置如式(6)所示。
若已知局部坐标系下的运动 RLCS、TLCS,则全局坐标系下的运动 RWCS、TWCS如式(7)所示,式(7)将用于算法中将局部坐标系下的运动关系转换至全局坐标系。
2 面向基准与余量约束的配准算法
在实际加工过程中,精加工前的零件毛坯上通常已具有1 个或2 个基准,在零件的自适应加工中,必须保证待加工面与基准面的相对位置关系,在此约束下的配准称为面向基准约束的配准。常用的基准为平面基准或圆柱面基准,因此,本节将结合式(4)的余量约束条件,分别针对这2 种基准约束建立相应的配准模型。
2.1 面向基准平面约束的配准算法
平面基准是最常见的一类基准,在滑轨精加工之前,其导轨面的下侧面即为基准平面。该基准面在粗加工阶段已完成加工,且与零件内型面的位置直接相关。所提算法的基本思路是:首先,配准基准平面;其次,将所有点按平面配准后得到的旋转矩阵与平移矢量进行变换;然后,在基准平面上建立局部坐标系(局部坐标系的x 轴与y 轴平行于基准平面);再次,将待加工面上的检测点在局部坐标系下进行配准,配准过程中检测点仅能够沿局部坐标系的x 轴与y 轴平移与绕局部坐标系的z 轴旋转;最后,将局部坐标系下的配准结果转换至全局坐标系中。
式(8)为任意平面的数学表达,参数A、B、C 构成垂直于该平面的单位法矢:
对于式(8)所示的平面,若基准平面的检测点为pDi(pDi1, pDi2, pDi3),待加工面的检测点为pi(pi1, pi2,pi3)。空间上的点pDi可向空间内的任意平面求绝对距离如式(9)所示。通过式(10)求解点pDi到平面的最近距离的最小二乘解,可解得检测点pDi对应的平面为ΠDP: A1x+B1y+C1z+D1=0,相应的理论基准平面为Π: A0x+B0y+C0z+D0=0。



平面基准约束下的带余量的配准优化模型如式(18)所示,式(18)表示在平面基准的约束下,经过第一次变换测量点的平移方向需平行于基准平面,测量点的旋转轴平行于平面基准的法矢。
式(18)计算完成后,通过式(7)求解全局坐标系下对应的旋转矩阵与平移矢量。
2.2 面向基准圆柱面约束的配准算法
基准圆柱面是指在实际零件的加工中存在着一个基准孔或基准轴的情况。为了保证加工后的曲面相对于基准孔或基准轴的位置,需要在检测基准圆柱面的基础上保证已加工的基准圆柱面与理论基准圆柱面同轴,在此基础上再进行待加工区域的配准。空间内任意圆柱面为

同样利用式(15)将待加工面的检测点pi进行变换,并得到点,该变换在全局坐标系下进行。随后,以圆柱基准中心轴矢量e0与pCOL点为基础建立局部坐标系LCS,使用式(16)将全部第1 次变换后的检测点 p1i及对应的理论点 qi变换至局部坐标系下。
式(18)可用于表示基准圆柱面约束下带余量的配准优化模型。此时,式(18)中矩阵 RLCS对应的旋转运动同样仅具有一个自由度,通常情况下为绕局部坐标系的e3轴的旋转运动(此时e3与圆柱基准中心轴矢量e0相同),矢量 TLCS对应的运动则改变为沿e3轴的平移运动。式(18)变换模型说明,在圆柱面基准的约束下,经过变换的测量点 pLiCS的平移方向与圆柱面中心轴平行,测量点可绕圆柱面中心轴进行转动,配准后的毛坯姿态需满足各测量点对应的加工余量大于限定值。求解式(18)后,通过式(7)求解对应的全局坐标系下的旋转矩阵与平移矢量。
2.3 面向基准平面约束与基准圆柱面约束的配准算法
在某些零件的配准过程中存在着同时使用基准面与基准孔进行定位的情况,这种情况必须保证基准平面与基准孔互相垂直。基于基准平面约束与基准圆柱面约束的旋转矩阵RG与平移矢量TG的求解流程如图2 所示。
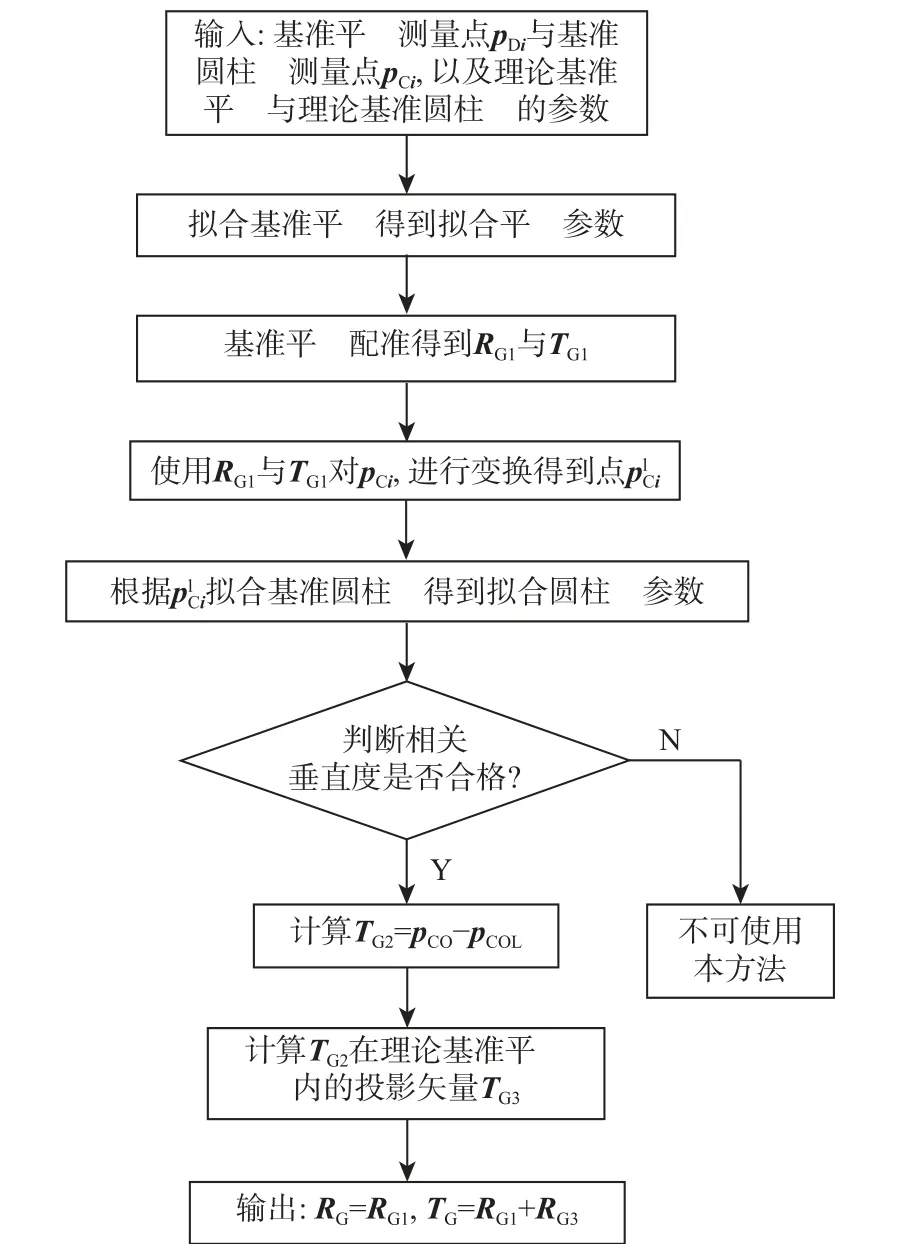
图2 基于基准约束下的变换矩阵与平移矢量求解流程Fig.2 Process of solving transformation matrix and translation vector based on datum constraints
首先,输入基准平面与基准圆柱面的测量点与理论曲面;随后,根据基准平面的测量点拟合基准平面,并根据式(13)与式(14)求解将拟合基准平面变换至理论基准平面的旋转矩阵RG1与平移矢量TG1;根据式(15)将基准圆柱面的测量点进行变换,并拟合基准圆柱面;根据拟合基准圆柱面的中心轴方向与拟合基准平面的法矢方向,判断基准平面与基准圆柱面是否满足垂直度要求,若不满足则判断此基准圆柱面需要在加工后进行修整,若垂直度满足要求则根据基准圆柱面的底面圆心的理论值与实测值求解平移矢量TG2及其投影矢量TG3;随后输出旋转矩阵RG与平移矢量TG用于变换待加工面上的检测点pi。本过程始终在全局坐标系下进行数据处理,处理过程中可对零件的状态进行过程检测,避免关键尺寸在终检中出现不合格再返修的情况。
同样利用式(15)将待加工面的检测点pi进行变换,得到点 p1i。以理论圆柱基准中心轴与理论平面基准Π 建立局部坐标系LCS,使用式(16)将全部的检测点 p1i及对应的理论点 qi变换至局部坐标系下。
在平面基准与圆柱面基准的双重约束下带余量的配准模型如式(22)所示,矩阵 RLCS对应的旋转运动仅具有一个自由度,通常情况下为绕局部坐标系e3轴的旋转运动,无平移运动。
式(22)计算完成后,通过式(7)求解全局坐标系下的旋转矩阵与平移矢量。
2.4 面向基准约束的配准模型求解算法
通过在机测量技术得到基准面上的检测点与待加工面上的检测点后,进行面向基准约束配准模型的求解流程如图3 所示。首先,将基准面上的检测点向基准面进行配准,得到矩阵RG与矢量TG,并建立相应的局部坐标系;然后,对待加工面上的点进行处理,将实测点与理论点变换至局部坐标系下;根据零件的余量情况进行带余量、少自由度的配准;最后,将局部坐标系下计算得到的旋转矩阵与平移矢量进行处理,得到全局坐标系下的旋转矩阵R2与平移矢量T2,输出使用的旋转矩阵(R2R1)与平移矢量(R2T1+T2)。通过基准约束降低了求解配准模型过程中变量的数量,可以保证配准后的零件基准面满足工艺需求。
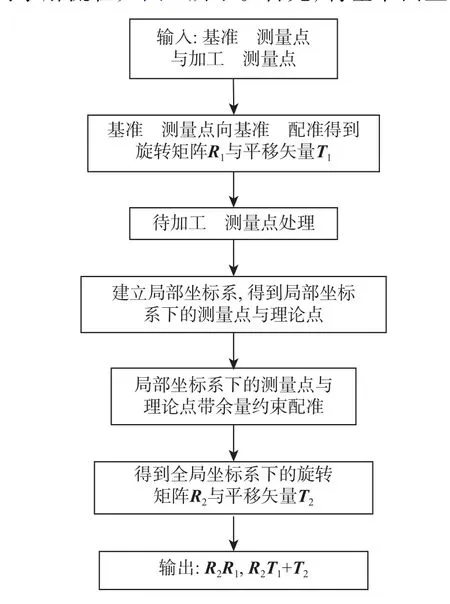
图3 面向基准约束的配准模型求解流程Fig.3 Process of solving registration model based on datum constraints
3 算例分析
通过vs2010 对本文所提算法进行开发,并在此基础上针对某典型零件“襟翼滑轨”的简化模型进行计算仿真,该简化模型如图4 所示。
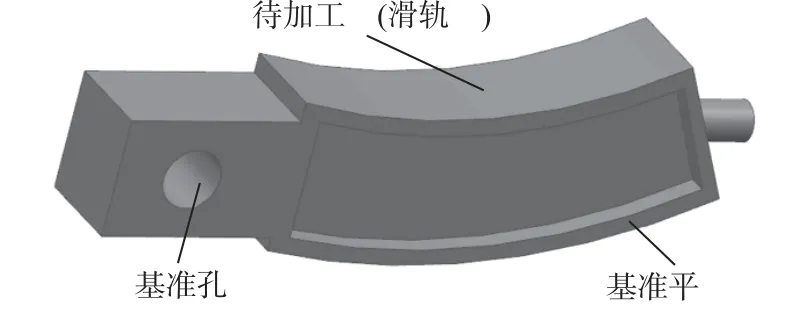
图4 具有典型特征的零件模型Fig.4 Design model with typical features
该零件在精加工阶段最重要的加工工序是加工襟翼滑轨的导轨面,即图4 中标识的待加工面。待加工面在精加工前具有一定的加工余量,在完成加工后必须与图4 中的基准平面、基准孔(即基准圆柱面)之间保持较高的位置精度,且精加工前基准平面已完成加工。
为了测试本文所提算法,可如图5 所示规划测量点,测量点分布在基准平面、基准圆柱面与待加工面上。使用基准平面作为约束,进行基于平面基准约束与余量约束的配准,解得旋转矩阵与平移矢量后将实测点向理论点进行变换,得到变换后的结果如图6 所示。对应点之间的误差如图7 所示,由图7 可知,在平面基准的约束下,可保证平面基准上测量点误差较小且平均,并保持待加工面具有较为平均的余量,但基准孔存在较大的偏差,具体数据如表1 所示。其中,方法1 为基准平面约束与余量约束下的配准结果,方法2 为基准平面、基准孔与余量约束下的配准结果,方法3 为仅余量约束下的配准结果。所提算法适用于基准面加工合格、基准孔留有足够余量的毛坯精加工,可在加工完待加工面后重制基准孔,从而保证曲面相对于基准的位置度。
图5 零件表面检测点分布Fig.5 Measuring points on surfaces of part
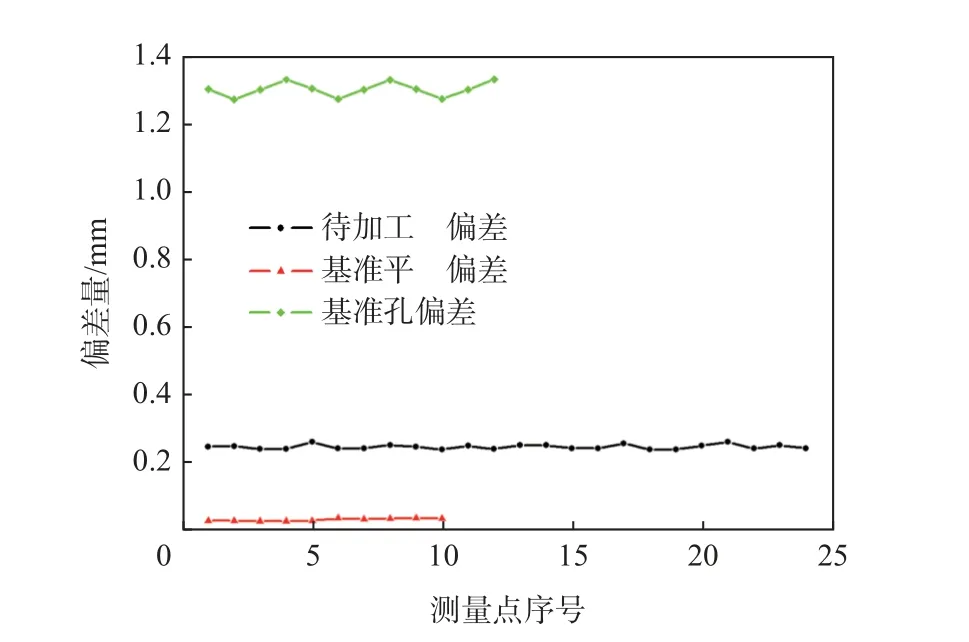
图7 在基准平面约束下配准后偏差曲线Fig.7 Deviations of different points after applying registration method based on constraint of a plane
使用基准平面与基准圆柱面作为约束,并在余量约束下进行加工面的配准,得到变换后的结果如图8 所示,相关点之间的误差如图9 所示。由图9可知,在基准平面与基准孔的双重约束下,可保证基准平面与基准孔上的测量点误差较小且平均,并保持待加工面具有较为平均的余量,待加工面上余量的波动小于0.03 mm,具体数据如表1 所示。所提算法适用于基准面与基准孔加工精度都合格的毛坯精加工,保证了滑轨面加工后相对于2 个基准的位置度。
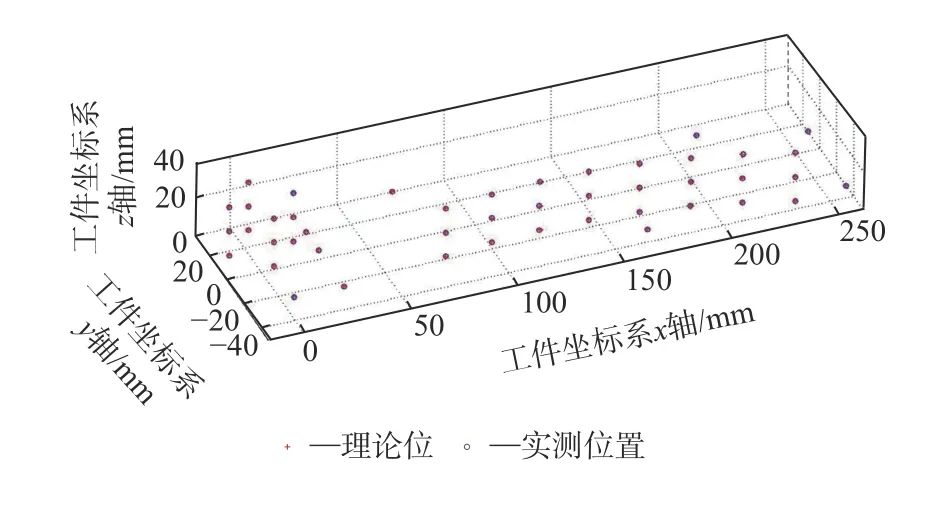
图8 在基准平面与基准圆柱面约束下的配准结果Fig.8 Registration result of method based on constraint of a plane and a cylinder
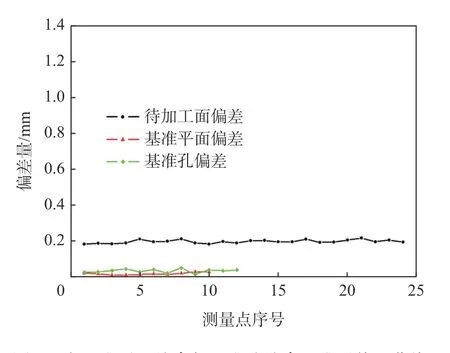
图9 在基准平面约束与基准孔约束配准后偏差曲线Fig.9 Deviations of different points after applying registration method based on constraint of a plane and a cylinder

表1 不同方法配准结果比较Table 1 Comparison of different registration method
在无基准约束的情况下,仅通过余量约束进行加工面的配准,得到变换后的结果如图10 所示,相关点之间的误差如图11 所示。由图10 可知,在无基准约束的情况下,待加工面虽可以保持较为平均的余量分布,但基准位置已出现偏差较大或偏差波动较大的情况,具体数据如表1 所示。无基准约束的情况下,为了保证滑轨面加工后相对于基准的位置度,需在待加工面加工完成后重制基准面与基准孔。
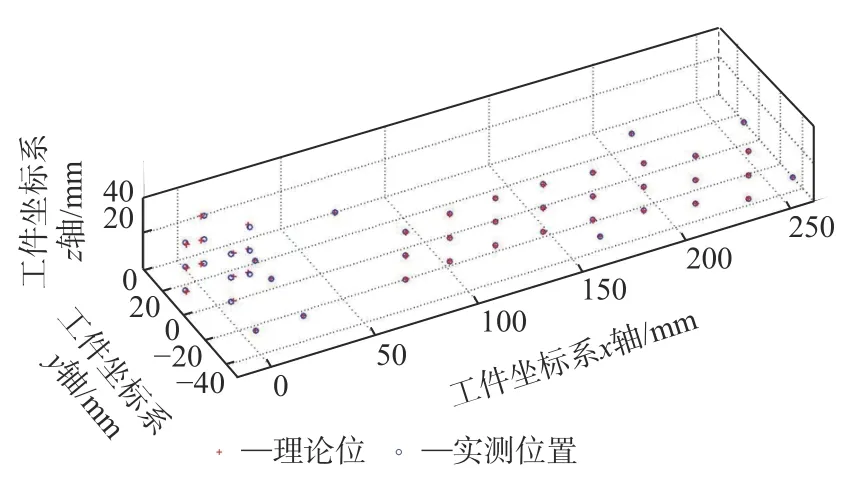
图10 余量约束下配准结果Fig.10 Registration result of method based on allowance constraints
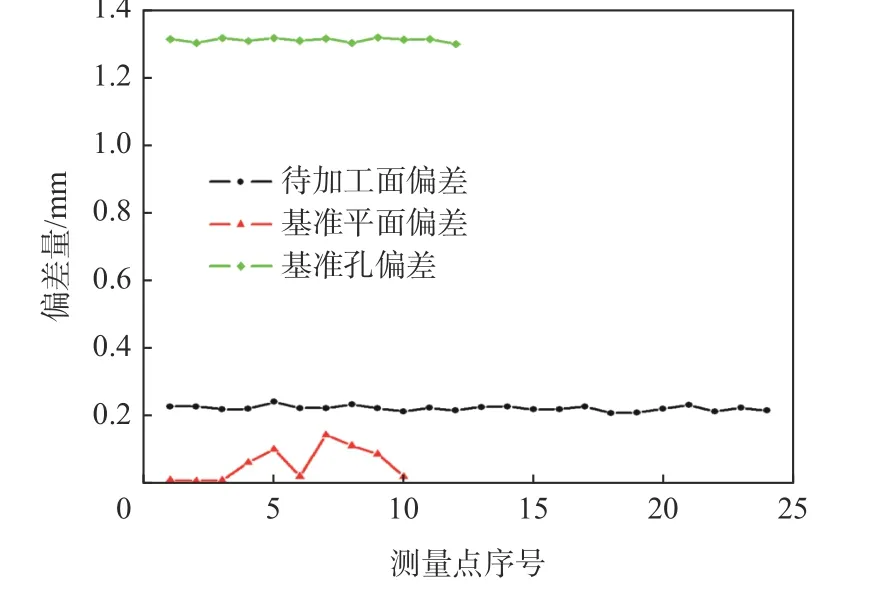
图11 仅余量约束下配准后偏差曲线Fig.11 Deviations of different points after applying registration method based on allowance constraints
由表1可知本文所提算法对保证零件待加工面的余量分布及加工后待加工面的位置精度有重要的意义。3 种方法的计算时间说明选用带基准约束的配准算法计算时间要短于无基准约束条件下的计算时间,方法1 的计算时间是方法3 计算时间的33.6%,偏差值波动量也更小。
4 结 论
1) 本文提出一种基于基准约束与余量约束的几何自适应配准算法,进行了相应的软件开发,并通过某滑轨零件的简化模型进行验证。
2) 本文所提算法分别在全局坐标系和局部坐标系内配准基准面和待加工面,可有效地保证待加工面相对于已加工基准的位置精度,提高产品加工的合格率。
3) 对于该襟翼滑轨零件来说,当同时使用基准平面约束与余量约束的配准方法时,得到的待加工面的余量最大、余量波动最小。因此,对于襟翼滑轨零件来说,基准平面加工完成、基准孔留有余量的毛坯最适合用于精加工。
4) 使用基准平面约束与余量约束的配准方法时,程序的计算时间最短,其计算时间是仅基于余量约束配准方法计算时间的33.6%。
