基于ANSYS 的O 形圈活动量对密封性能影响探究*

2023-03-30迟晓宁郭学平陈张斌王文虎陈艺昌王培杰

润滑与密封 2023年3期

迟晓宁郭学平陈张斌王文虎陈艺昌王培杰梁彬

（1. 广州机械科学研究院有限公司广东广州 510700； 2. 国营芜湖机械厂安徽芜湖 241007；3. 广州国机密封科技有限公司广东广州 510700）

O 形橡胶密封圈（以下简称O 形圈）因其制造简单、功能可靠，且安装容易，被广泛地应用于机床、船舶、汽车、航空航天等领域的机械设备上，是最常见的密封件之一[1-2］。但O 形圈在服役过程中，受外部恶劣条件的影响，如较为剧烈的温度和应力变化等，极易导致其发生脆化和老化，增大其与其他部件的摩擦力，从而导致渗漏等问题的出现。

O 形圈在动态应用过程中常发生扭转现象，即O形圈沿着周向扭转。引起扭曲损伤的原因很多，大多是由于活塞、活塞杆和缸筒的间隙不均匀、偏心过大、 O 形圈截面直径不均匀等造成。为探究某飞机某部位作动筒渗漏和密封圈扭转断裂的原因，本文作者通过分析密封圈使用工况，采用SolidWorks 和Ansys软件[3］进行建模，分析配合间隙、沟槽深度、沟槽宽度、圆柱度和偏载等因素[4］对密封性的影响，为作动筒性能改进提供理论参考。

1 O 形圈接触密封结构模型建立

1.1 基础模型尺寸

该飞机作动筒采用丁腈橡胶O 形圈接触密封形式，如图1 所示。其中缸内径D为ϕ28H7，公差为（0，＋0.021），沟槽槽底直径d的尺寸为ϕ24h8，公差为（-0.033， 0），活塞直径C为ϕ28 mm，沟槽宽度W为4 mm，单边径向间隙（配合间隙）S由缸筒内径D和活塞直径C的尺寸决定，最小间隙为0.01 mm，最大间隙为0.03 mm。由于O 形圈会在介质中发生溶胀，因此按照O 形圈线径2.5 mm，溶胀7%进行计算，得到O 形圈线径为2.675 mm。

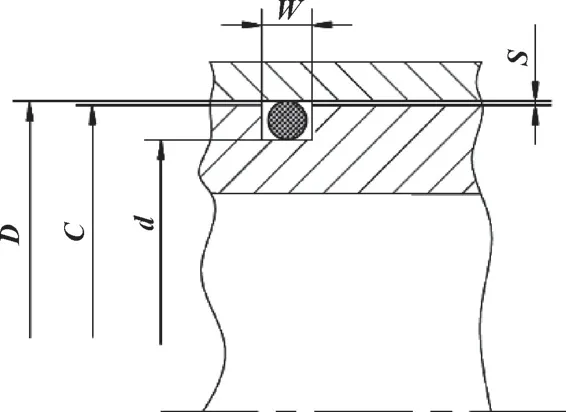
图1 活塞密封沟槽型式Fig.1 Piston seal groove type

活塞密封沟槽型式是典型的动密封形式[5］，上述参数共同决定了O 形圈密封性能的优劣。为了准确获得O 形圈的密封性能，将O 形圈及沟槽作为整体进行分析，由于该密封结构具有轴对称性，因此将其简化为二维轴对称模型来进行分析。根据结构尺寸，使用SolidWorks 建立模型，如图2 所示。

图2 密封结构模型Fig.2 Seal structure model

1.2 模型假设、边界条件与接触定义

为了保证模拟结果的准确，在建立O 形圈密封结构有限元模型之前，首先做以下几点假设[6］：

（1）弹性体丁腈橡胶（NBR）具有确定的应力应变性能；

（2）沟槽刚度是O 形圈的几万倍，不考虑沟槽的变形；

（3） O 形圈结构具有轴对称性；

（4）丁腈橡胶拉伸与压缩蠕变性质相同。

O 形圈所用材料为丁腈橡胶，其相关材料弹性模量为8.92 MPa，泊松比为0.499。对于超弹性材料，除定义材料弹性模量和泊松比外，可用Mooney-Rivlin 模型[7-9］来表征其材料性能，通过提供的丁腈橡胶制备标准试样进行拉压试验，然后在ANSYS 中进行曲线拟合，如图3 所示，获得丁腈橡胶材料的Mooney-Rivlin 系数C10＝0.75 MPa，C01＝1.89 MPa。

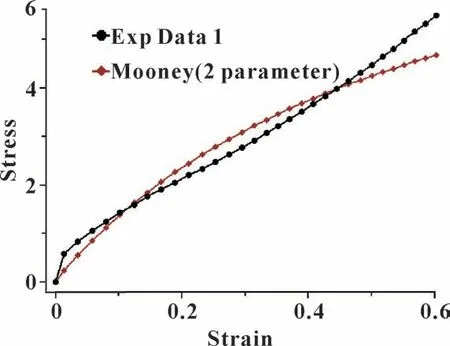
图3 ANSYS 拟合丁腈橡胶数据Fig.3 ANSYS fitting data of NBR

由于在有限元分析中需考虑丁腈橡胶的不可压缩性，因此选择了PLANE182 单元进行了网格划分，并对局部网格进行了细化，局部网格细化后的有限元模型如图4 所示。

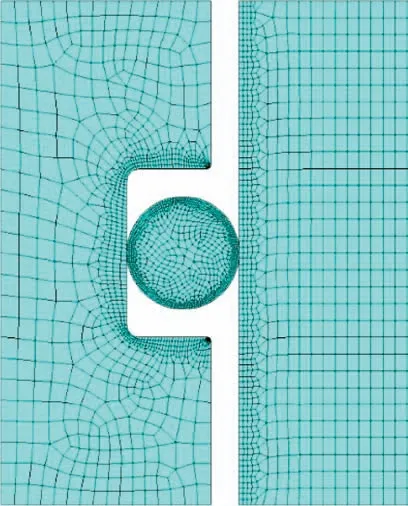
图4 密封结构有限元模型Fig.4 Finite element model of seal structure

在装配状态下， O 形圈与活塞和缸筒均有接触，由于活塞和缸筒的刚度远大于O 形圈，因此在建立接触对时以活塞和衬套面为目标面， O 形圈面为接触面，共建立2 个接触对，如图5 所示。在ANSYS 中，模型初始状态并不处于装配状态，需要通过位移约束[10］实现最终的装配。通过在不同分析步中定义部件的轴向、径向位移，实现对密封结构的位置固定和过盈压缩，完成装配。

2 仿真结果及分析

配合间隙、沟槽深度、沟槽宽度、圆柱度和偏载均有可能导致O 形圈密封结构出现故障，为了找出发生渗漏和扭转断裂的主要原因，分别探讨上述参数对密封性能的影响。模型需要通过位移约束实现最终的装配，因此所有的模拟结果均对装配状态和静压状态进行探讨，如图6 所示。

2.1 配合间隙对密封性能的影响

配合间隙指缸内径与活塞杆直径的距离，对装配过程中所发生的位移并无影响，因此对装配状态下O形圈的应力、变形等并无影响。但配合间隙不同，承压状态下的O 形圈变形不同，接触压力也有所不同[11-12］。图7 示出了O 形圈在静压状态下不同配合间隙的接触压力分布。可见，在沟槽侧壁间隙处，随着配合间隙增大， O 形圈挤入间隙的体积变大。

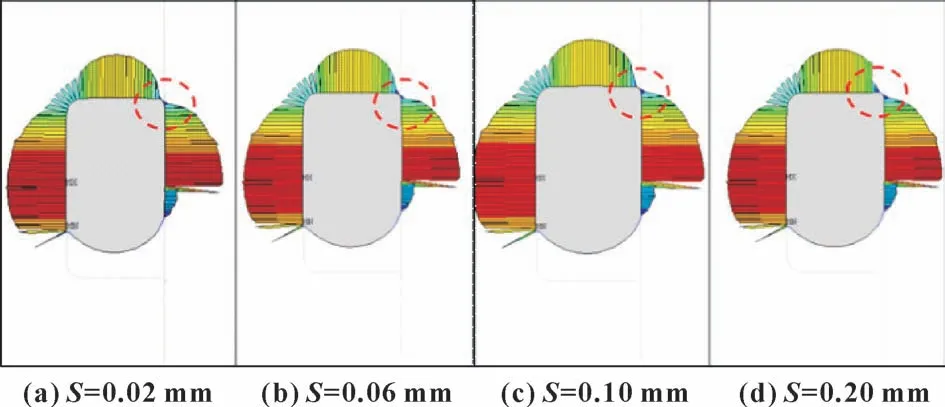
图7 O 形圈在静压状态下不同配合间隙的接触状态Fig.7 Contact of O-ring with different fit clearance under static pressure：（a） S＝0.02 mm；（b） S＝0.06 mm；（c） S＝0.10 mm；（d） S＝0.20 mm

对图7 中圆圈处的某一固定位置节点进行应力分析，结果如表1 所示。可知，随着配合间隙的增大，节点的等效应力、接触压力和接触摩擦力也随之增大，一旦表面超过其许用值，材料表面会被破坏，其密封效果变差。因此，在允许的范围内，配合间隙越小越好。根据表1 数据，建议间隙在0.02 ～0.10 mm范围内，配合间隙小有利于密封。

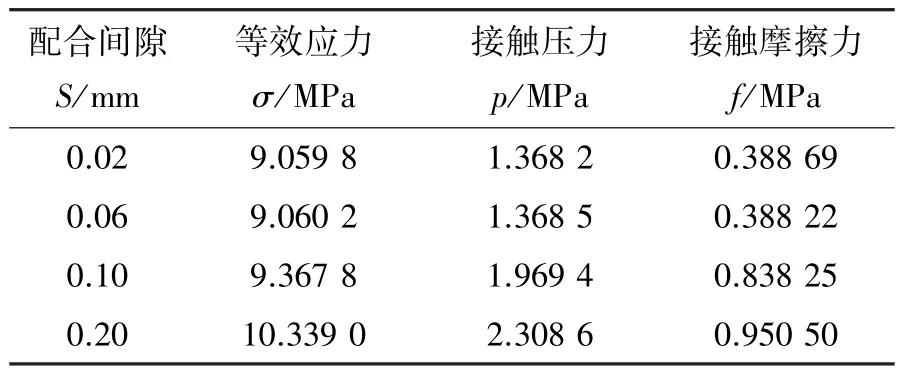
表1 不同配合间隙下节点应力计算结果Table 1 Calculation results of joint stress of different fit clearance

2.2 沟槽深度对密封性能的影响

沟槽深度是指活塞密封的沟槽槽底直径与活塞直径之间的距离，直接影响O 形圈最大变形宽度、最大接触压力和径向力。沟槽宽度W为4 mm 时，分别提取不同配合间隙下Y方向上的变形图和O 形圈变形后的最大宽度，如图8 所示，沟槽深度为2.04 mm时，装配状态下的O 形圈的Y方向变形图和von Mises 应力云图[13］。

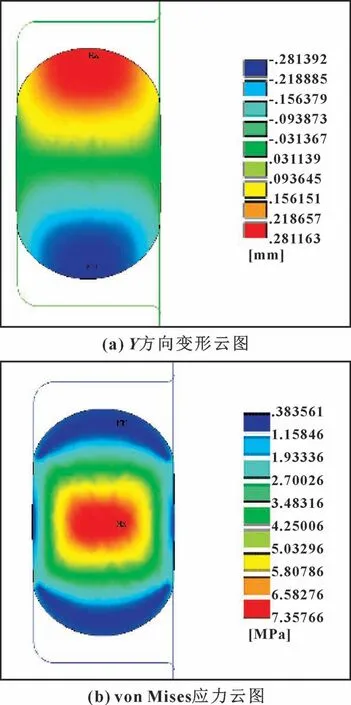
图8 装配状态下O 形圈Y 方向变形云图和von Mises 应力云图（h＝2.04 mm）Fig.8 Y-direction deformation nephograph （a） and von Mises stress nephograph （b） of O-ring under assembly state at groove depth h＝2.04 mm

图9 示出了沟槽深度与O 形圈最大变形宽度及沟槽宽度余量关系。改变沟槽深度即改变O 形圈预压缩量[14］，随着沟槽深度增大，预压缩量减小， O形圈的最大变形宽度逐渐减小，沟槽宽度余量逐渐增大。

图9 沟槽深度与O 形圈最大变形宽度及沟槽宽度余量关系Fig.9 Relationship between groove depth and maximum deformation width （a） and groove width margin （b） of O-ring

图10 示出了沟槽深度为2.04 mm 时，装配状态下的O 形圈的接触压力云图。可见，预压缩状态下，最大接触压力发生在O 形圈径向最大尺寸与活塞和缸筒接触处，接触压力的值沿着接触宽度向两侧依次减小，接触压力整体分布类似半圆形，且近似于O形圈径向中心尺寸面对称。

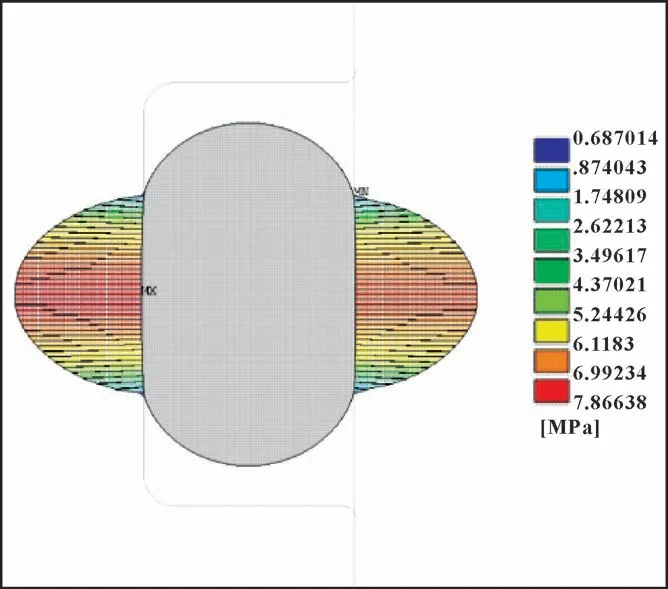
图10 装配状态下O 形圈接触压力云图（h＝2.04 mm）Fig.10 Contact pressure nephograph of O-ring under assembly state at groove depth h＝2.04 mm

文中分别仿真分析了不同沟槽深度下的接触压力，并最大接触压力，得到沟槽深度与O 形圈最大接触压力的关系，如图11 所示。可见，随着沟槽深度的增大， O 形圈的最大接触压力逐渐减小。

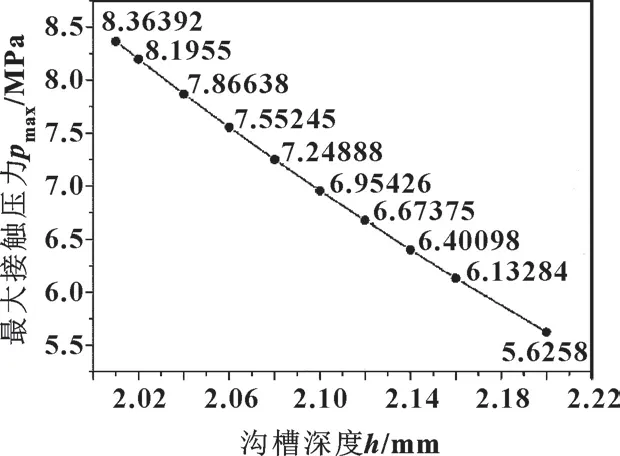
图11 沟槽深度与O 形圈最大接触压力关系Fig.11 Relationship between groove depth and maximum contact pressure of O-ring

径向力是指密封圈对缸筒的张紧力，是密封圈对缸筒接触压力的合力。 O 形圈的径向力随沟槽深度的变化如图12 所示，随着沟槽深度的增大， O 形圈的径向力逐渐减小。

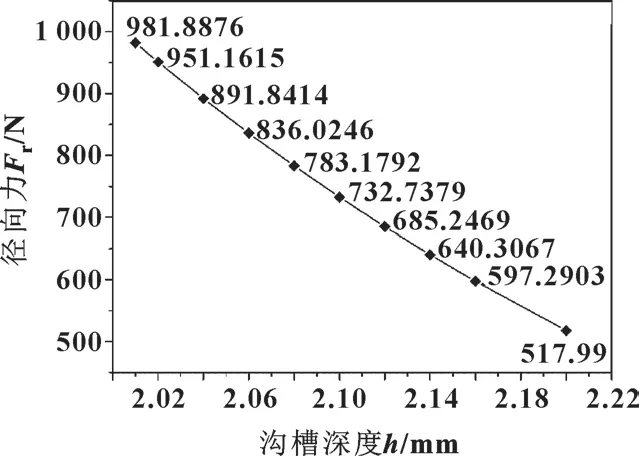
图12 沟槽深度与O 形圈径向力关系Fig.12 Relationship between groove depth and O-ring radial force

根据上述分析，沟槽深度影响O 形圈的变形宽度即与密封面的接触宽度、接触压力和径向力。沟槽深度越大， O 形圈的接触压力和径向力越小，进而能够提供的抵抗O 形圈发生扭转变形的力就越小，当径向力小于一定值时， O 形圈在沟槽中发生扭转，所以沟槽深度应该控制在一个合理范围内。结合仿真数据和SAE AS4716-2017C，建议维修后沟槽深度值小于2.06 mm。

2.3 沟槽宽度对密封性能的影响

沟槽宽度为4 mm 时O 形圈在装配状态和静压状态下的von Mises 应力云图如图13 所示。在装配状态下（纯挤压） von Mises 应力相对较大的区域分布类似矩形状，最大值为6.96 MPa，出现在O 形圈径向最大尺寸与衬套接触区域向内一段距离处。从图13 （b）可以看出，当有油液压力作用在O 形圈后， O形圈被推动而“流向” 沟槽侧壁处，并与沟槽侧壁向接触，该区域附近的应力值变大，最大接触应力出现在O 形圈与活塞壁接触区域，最大值29.36 MPa。

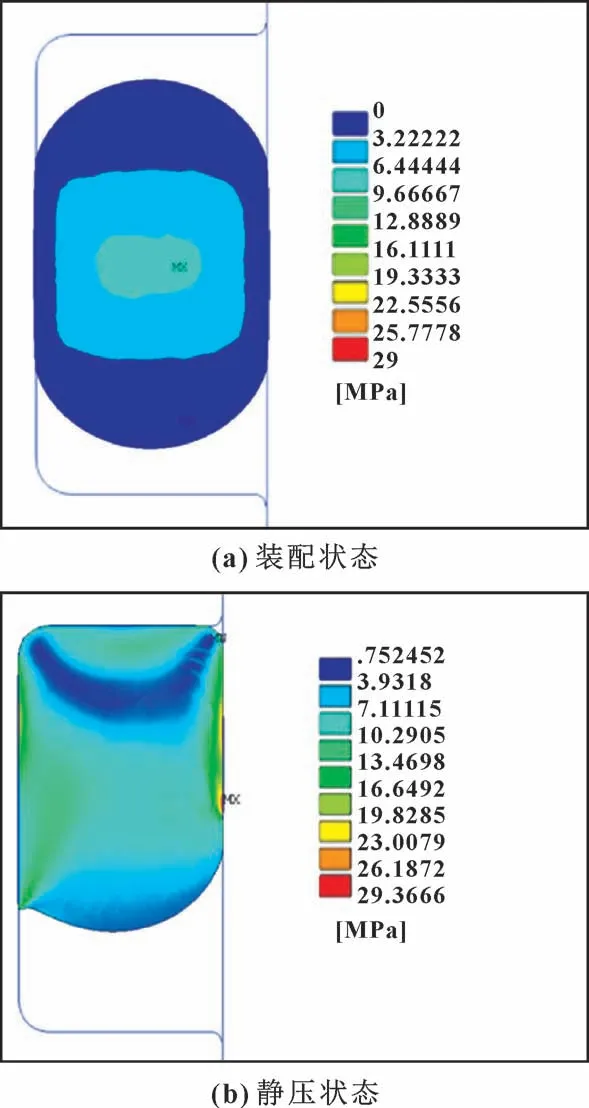
图13 von Mises 应力云图Fig.13 von Mises stress nephogram：（a） assembly state；（b） static pressure state

根据2.1 节的分析结果，可知当沟槽深度H＝2.06 mm 时， O 形圈最大变形宽度T＝3.206 mm，即当沟槽宽度为3.206 mm 时， O 形圈恰好接触沟槽壁。在前述条件下，通过改变沟槽宽度W探究沟槽宽度对密封性能的影响。

表2 列出了不同沟槽宽度、不同工作状态下最大von Mises 应力和最大接触压力的模拟结果。随着沟槽宽度的减小， O 形圈的体积填充率增大。装配状态下，当沟槽宽度大于3.2 mm 时，接触压力仅产生在活塞壁和沟槽底侧，且最大接触压力不发生变化，约为7.55 MPa。当沟槽宽度小于等于3.2 mm 时，沟槽两侧壁也产生接触压力，最大接触压力随沟槽宽度的减小而增加。沟槽宽度的减小，限制了O 形圈在沟槽内的游动，避免O 形圈发生滚动。与装配状态下相比，静压状态下随O 形圈与活塞和缸筒的接触宽度增加，接触面增大，与沟槽侧壁也有了接触，当沟槽宽度大于3.2 mm 时，橡胶密封圈会在沟槽内游动，沟槽越宽，密封圈游动范围也越大，其接触压力也增大。当沟槽宽度小于等于3.2 mm 时，橡胶密封圈的填充率越来越高，其最大接触压力也有略微增加。当沟槽宽度过小，即沟槽截面过小，密封圈的截面填满了沟槽的截面，那么运动时的摩擦阻力将会特别大，尽管O 形圈无法滚动，但也会引起严重的磨损。

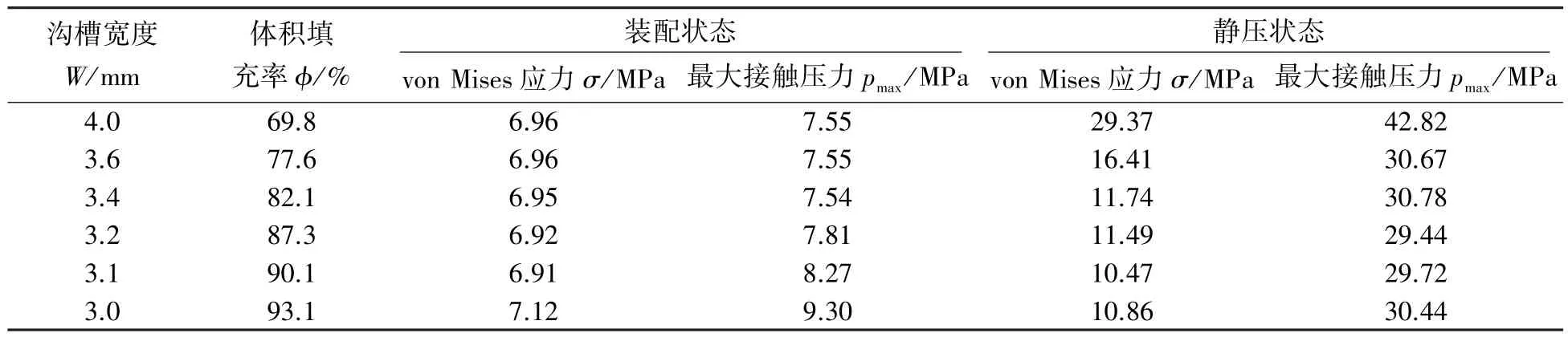
表2 不同沟槽宽度、不同工作状态下von Mises 应力和最大接触压力的计算结果Table 2 The calculation results of von Mises stress and maximum contact pressure under different groove widths and different operating conditions

根据航标HB-Z4—1995 《O 形密封圈及密封结构的设计要求》，密封槽的宽度非常重要。密封槽太宽，限制不了挡圈的倾斜，失去保护作用，且会增加密封的空行程。密封槽太窄，会产生很大的摩擦力，也可能使密封圈材料挤入间隙，并给装配带来很大困难，因此应合理的选择槽宽W。

根据HB-Z4—1995，有

其中K为胶料的槽宽系数。按照要求，活动密封的槽宽系数应为1.15～1.25，设计时取密封槽宽为4.6 mm 进行计算，除去一侧1.0 mm 宽的挡圈，实际用于固定O 形圈的宽度为3.6 mm。 O 形圈截面直径为2.675 mm，则槽宽系数为1.35，槽宽系数大于标准；若取O 形圈截面直径为2.5 mm，则槽宽系数为1.44，槽宽系数也大于标准。所以，作动筒工作时，活塞快速响应，密封圈在间隙中可能会发生翻滚，导致密封圈扭转出现扭转断裂。因此，密封槽宽度尺寸选择过大是造成密封圈断裂的主要因素之一。

结合表2 数据可知，建议不加挡圈时的沟槽宽度为3.1 ～3.4 mm，此时的体积填充率为90.1% ～82.1%，承压状态下的von Mises 应力约为11 MPa。

2.4 圆柱度对密封性能的影响

圆柱度指任一垂直截面最大尺寸与最小尺寸差。圆柱度误差指实际圆柱面要素对其理想圆柱面的变动量。根据圆柱度的定义，建立仿真模型，通过改变d的值探究圆柱度对密封性能的影响。

为控制单一变量，设定沟槽深度H＝2.06 mm，沟槽宽度W＝3.4 mm，利用ANSYS 软件进行仿真分析，得到的数据如表3 所示。可知，随着圆柱度的增大，其径向力和最大接触压力略微减小。因此，圆柱度在合理的范围内变化时，对密封性能的影响可忽略不计。

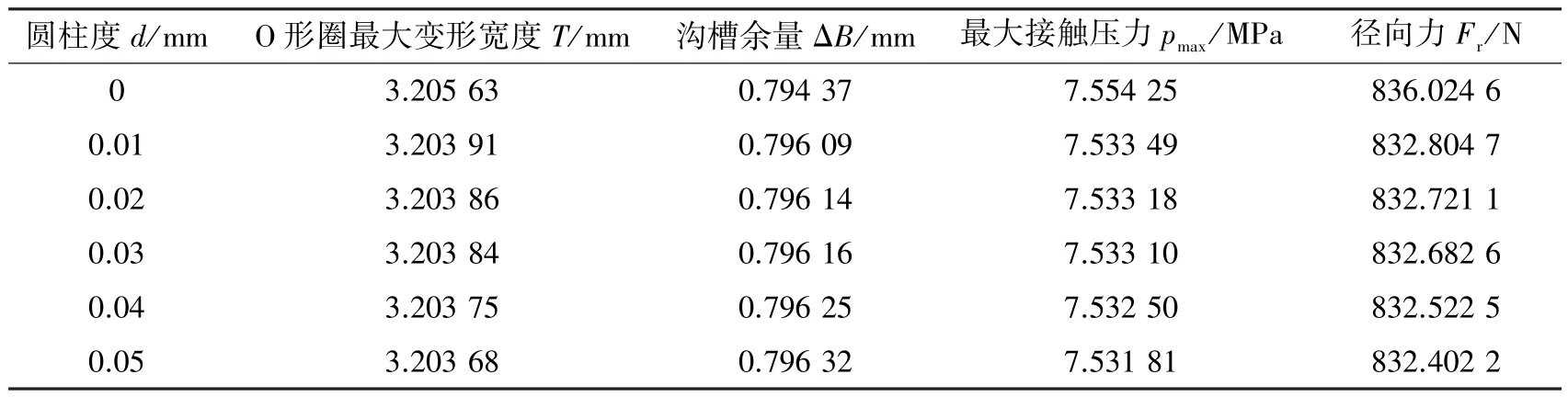
表3 不同圆柱度下的计算结果Table 3 Calculation results under different cylindricity

2.5 偏载对密封性能的影响

该作动筒在工作时会有摆动，因此会有偏载，从而引起偏心，造成O 形圈压缩量不均匀，可能会导致O 形圈失效。

缸筒的外径尺寸为ϕ28f7，活塞的内径尺寸为ϕ28H7，故最小间隙为0.020 mm，最大间隙为0.062 mm，所以最小偏心为0.020 mm，最大偏心为0.062 mm。

文中对于O 形密封圈在偏心情况下的分析仍在二维平面上进行，通过取偏心后密封圈的最大和最小压缩量作为二维模型的压缩量进行计算，结果如表4所示。

表4 不同偏心量下O 形圈的最大von Mises 应力和最大接触压力Table 4 Maximum von Mises stress and maximum contact pressure of O-rings with different eccentricities

当其偏心量最大为0.062 时，其最大压缩下的最大von Mises 应力和最大接触压力与偏心量为0 时的偏差分别为7.72%和5.16%，最小压缩下的最大von Mises 应力和最大接触压力与偏心量为0 时的偏差分别为-3.68%和-4.22%，在可接受的范围内，且O形圈挤出不明显，所以该范围内的偏心量对其密封性能影响不大。