基于气候因子的杉木单木胸径生长模型构建

2023-03-30郭常酉郭宏仙王宝华

南京林业大学学报（自然科学版） 2023年1期

郭常酉，郭宏仙，王宝华*

(1.国家林业和草原局宣传中心，北京 100013；2.宁夏大学农学院，宁夏银川 750021)

预测不同经营措施下林分的生长动态对于制定正确的森林经营决策进而科学管理森林十分重要。森林生长和收获模型是研究林分及单木生长动态变化的有效工具[1]。其中，单木生长模型作为森林生长和收获模型的重要组成部分之一，与全林分模型和径阶分布模型相比，更能直观、详细地描述林分结构和反映林木生长过程，尤其是在混交林中[2]。

单木胸径生长模型常常表达为与林木大小、竞争和立地条件相关的线性函数，采用传统的分析方法，即最小二乘法(OLS)进行模型的构建[3]。但是，原则上，最小二乘法的准确使用需要数据满足独立、正态分布和等方差的统计假设[4]。而林业建模数据常常具有连续观测(同一树木多次观测)和层次性(树木—样地—区域)等特点，难以满足上述假设，会导致对参数标准误差的有偏估计[5]。而混合效应模型作为处理多层次重复测量数据的有效工具，被广泛应用于森林生长和收获模型中，如单木胸径生长模型[6]、冠幅模型[7]和胸径-树高模型[8]。混合效应模型的使用显著提高了模型的预估精度。

由于森林对光照、温度和降水有一定的敏感性，单木的径向生长也受到气候变化的影响[9]。因此，树木生长不仅受林木大小、竞争和立地条件影响，还与温度和降水等气候因子息息相关。很多研究表明，树木生长季温度和降水的变化与树木生长量在统计上存在显著相关性，可以用来描述树木的生长[10-11]。然而，当前对基于气候因子的单木胸径生长模型的研究还比较少。因此，在气候变化背景下，构建包含气候因子的单木胸径生长模型以探究气候变化对于胸径生长的影响十分重要。

杉木(Cunninghamialanceolata)是我国南方重要的商品用材林树种，广泛分布在我国亚热带地区[12]。作为湖南省主要优良速生用材树种，根据第八次全国森林资源连续清查结果显示，杉木林面积和蓄积量分别为2.088×106hm2、1.178×108m3，占湖南省森林面积和蓄积量的26.14%和28.93%[13]。杉木具有生长速度快、丰产、木材经济价值高等优良特性，是上等的建筑材、工业板材、造船材等，同时也广泛使用在造纸、家具等行业。此外，杉木的枝、叶和皮还可以作为药材使用。杉木除了有较高的经济效益，还具有重要的生态价值，在固碳、水源涵养、生物多样性保护、净化大气环境等方面发挥着重要作用[14]。

本研究以湖南省杉木林为研究对象，基于第七、八次全国森林资源连续清查中73块样地的3 638株杉木数据，运用多元逐步回归的方法，考虑林木大小、竞争、立地条件及气候因子对杉木胸径生长的影响，分析4个因变量即5年胸径增长量、5年胸径增长量的自然对数、5年胸径平方增长量的自然对数、胸径平方增长量，确定最优基础模型。在最优模型的基础上，引入样地随机效应，构建单水平线性混合效应模型，并引入3种异方差函数和3种自相关结构来消除异方差和自相关，最后采用十折交叉验证的方法对模型的预测效果进行检验，以期构建的单木胸径生长模型能为研究区杉木的生长和经营管理提供科学依据。

1 材料与方法

1.1 研究区概况

研究区位于中国中南部(108°47′～114°15′E，24°38′～30°08′N)，长江中下游。境内地形复杂，主要有丘陵、低山、平原等，海拔为24～2 099 m。典型的大陆性中亚热带季风湿润气候，年平均气温16～19 ℃，无霜期253～311 d，年日照时长为1 300～1 800 h；水量充沛，年平均降水量1 200～1 700 mm。土壤主要为红壤和黄壤，此外，石灰土和紫色土也有少量分布。研究区植被资源丰富，主要乔木树种有马尾松(Pinusmassoniana)、杉木(Cunninghamialanceolata)、柏木(Cupressusfunebris)、湿地松(Pinuselliottii)、青冈栎(Cyclobalanopsisglauca)、樟树(Cinnamomumcamphora)、枫香(Liquidambarformosana)、甜槠(Castanopsiseyrei)、鹅耳枥(Carpinusturczaninowii)、锥栎(Castaneahenryi)、木荷(Schimasuperba)等。

1.2 数据来源

数据来源于湖南省第七(2009年)、八(2014年)次国家森林资源连续清查数据，共筛选出满足要求的样地73块，共有杉木3 638株。样地筛选原则如下：①样地郁闭度0.7以上；②剔除采伐过量、错测木过多的样地。样地为正方形，面积0.066 7 hm2，样地调查因子主要包括海拔、坡向、坡位、坡度、土壤厚度、平均年龄、平均胸径、平均树高、郁闭度等；样木调查因子主要包括样地号、样木号、树种、胸径(≥5 cm)、相对位置等。具体的样地和样木因子见表1。

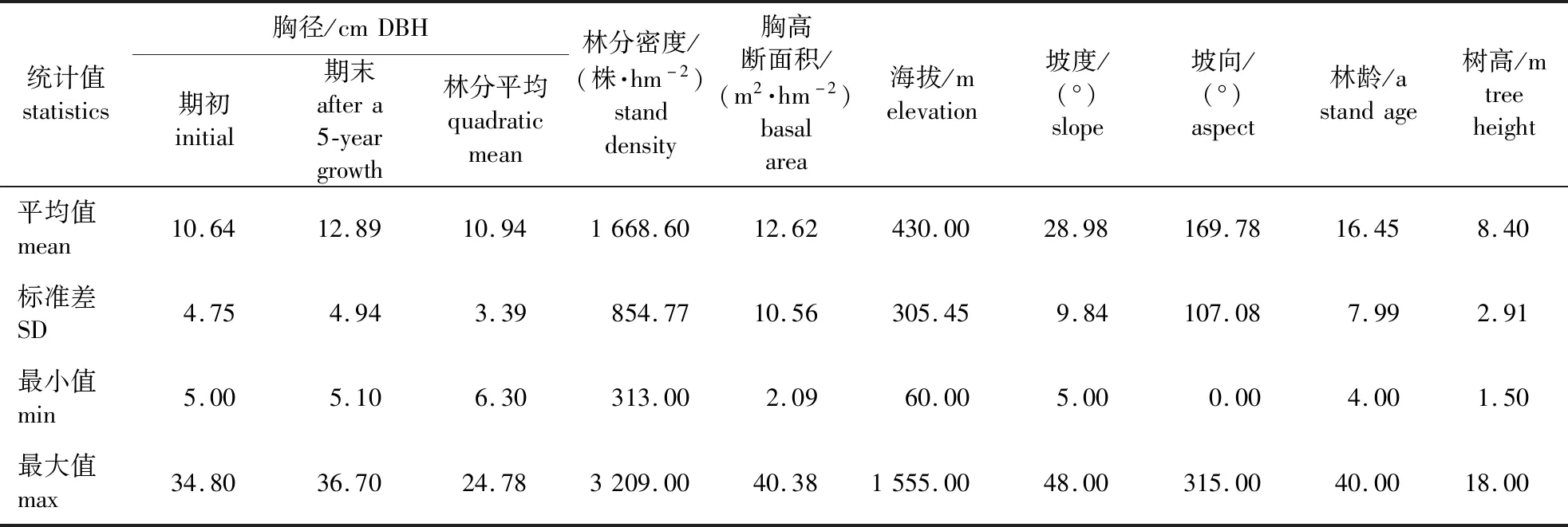
表1 杉木建模数据基本统计量Table 1 The statistics of modeling data for Cunninghamia lanceolata

各样地每年的气候因子通过输入各样地经纬度坐标和海拔利用ClimateAP v2.10 软件提取获得，然后对5年的变量进行平均计算，供建模使用[15]。具体气候因子见表2。

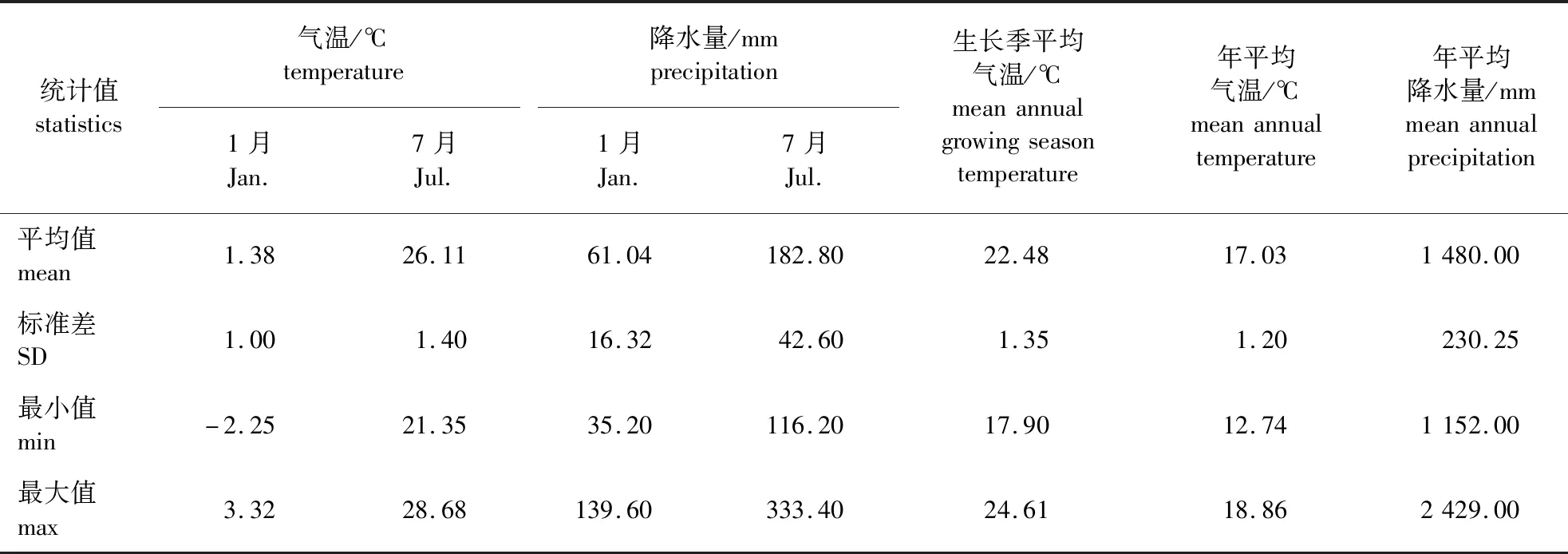
表2 样地气候因子统计量Table 2 The statistics of climate factors in the study area

1.3 模型构建

1.3.1 基础模型构建

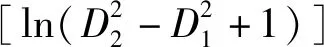
2)自变量的选择。大量研究表明单木胸径生长常常受到林木大小、竞争、立地及其他林分因子的影响[2,17-18]，本研究充分考虑以上变量，并在此基础上引入气候因子。因此，本研究单木胸径生长量表达为如下函数：

y=f(xsize+xcompetition+xsite+xstand+xclimate)。

(1)

其中：xsize为林木大小变量；xcompetition为林木竞争变量；xsite为立地因子变量；xstand为其他林分因子变量；xclimate为气候因子变量。

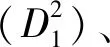
竞争变量：林木之间的竞争是影响树木生长的一个重要因素，它决定单木胸径生长的趋势[9]。通常来讲，在竞争中处于优势地位的林木，对水分、光照、营养物质等的获取机会更大，生长更快。竞争指数包括与距离相关的竞争指数和与距离无关的竞争指数[20]，本研究为了使模型具有更好的普适性，选择了以下与距离无关的竞争株数：大于对象木的胸高断面积之和(SBAL1)、大于对象木的胸高断面积之和与对象木胸径之比(SBAL1/D1)。

立地及其他林分因子：除了林木大小、竞争之外，立地条件和其他林分因子也是影响林木生长必不可少的因素之一。本研究选择了每公顷株数(N1)、每公顷断面积(SBA1)、相对密度指数(对象木期初胸径与期初林分平均胸径之比，DR1=D1/Dg1)、海拔(SEL)、坡度(SSL)和坡向(SASP)。此外，根据Stage[21]的研究将海拔、坡度和坡向进行了组合，即坡向正弦值与海拔对数之积(SLN=sinSASP·lnSEL)、坡向余弦值与海拔对数之积(CLN=cosSASP·lnSEL)、坡度正切值与坡向正弦值之积(TSIN=tanSSL·sinSASP)、坡度正切值与坡向余弦值之积(TCOS=tanSSL·cosSASP)。

气候因子：研究表明气候因子也与单木胸径生长密切相关。引入年平均气温(TMA1)、年平均降水量(PMA1)、生长季温度(Tgrowth)、7月平均最高温度(Tmax07)、1月平均最低温度(Tmin01)、7月平均降水量(PPT07)、1月平均降水量(PPT01)。

3)模型构建方法。采用多元逐步回归的方法进行基础模型的构建。在构建过程中结合相关系数的t检验和方法膨胀因子(VIF)进行自变量的选择。为避免自变量之间存在相关性，剔除VIF大于5的自变量，最终只有相关系数检验显著(P<0.05)和VIF值<5的变量进入模型。

为了对不同因变量的模型进行比较和评价，计算模型的决定系数(R2)、绝对误差(BIAS)和均方根误差(RMSE)。此外，采用十折交叉验证的方法对模型进行检验，并计算归一化均方误差(NMSE，式中记为σNMSE)和预测误差平方和(PRESS,式中记为σPRESS)来评价模型预估效果[22]。本研究为了使不同因变量所构建模型之间具有可比性，以上评价指标均转化为期末胸径进行计算。NMSE和PRESS的计算公式如下：

(2)

(3)

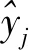
1.3.2 混合效应模型构建

1)模型形式。由于数据的分层结构和重复观测，本研究引入样地随机效应构建单水平线性混合效应模型。单水平线性混合效应模型的形式如下[23]：

(4)

其中：yi为杉木单木5年胸径生长量向量；Xi为包含林木大小、竞争、立地及气候因子变量的固定效应设计矩阵；β为固定效应参数向量；Zi为以样地为随机效应的设计矩阵；bi为随机效应参数向量；εi为误差向量；G为随机效应参数方差-协方差矩阵；σ2为模型的误差方差值；Ri为误差方差-协方差矩阵。

2)参数效应的确定。本研究参数效应的确定采用如下方法：将模型中的参数均看作随机效应参数，对所有组合进行拟合，根据模型的赤池信息准则(AIC)、贝叶斯信息准则(BIC)、-2倍的对数似然值(-2LL)以及似然比检验(LRT)确定最优的参数效应。

3)误差方差-协方差的确定。考虑到数据由于重复测量和层次性存在异方差和自相关问题，本研究定义了误差方差-协方差矩阵。样地内误差方差-协方差结构(Ri)如下：

(5)

其中：σ2为模型的误差方差值；Gi为异方差矩阵；Ti为自相关矩阵。

采用3种常用的异方差函数，即指数函数(exponent)、幂函数(power)和常数加幂函数(constpower)以及3种常用的自相关结构，即复合对称结构(CS)、自回归结构[AR(1)]和自回归移动平均结构[ARMA(1,1)]来消除模型异方差和自相关。

1.3.3 模型检验与评价

本研究采用十折交叉验证的方法对构建的单水平杉木单木胸径生长混合效应模型进行检验和评价，并利用R2、AIC、BIC以及LRT对基础模型和混合效应模型结果进行比较。

2 结果与分析

2.1 最优基础模型

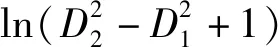
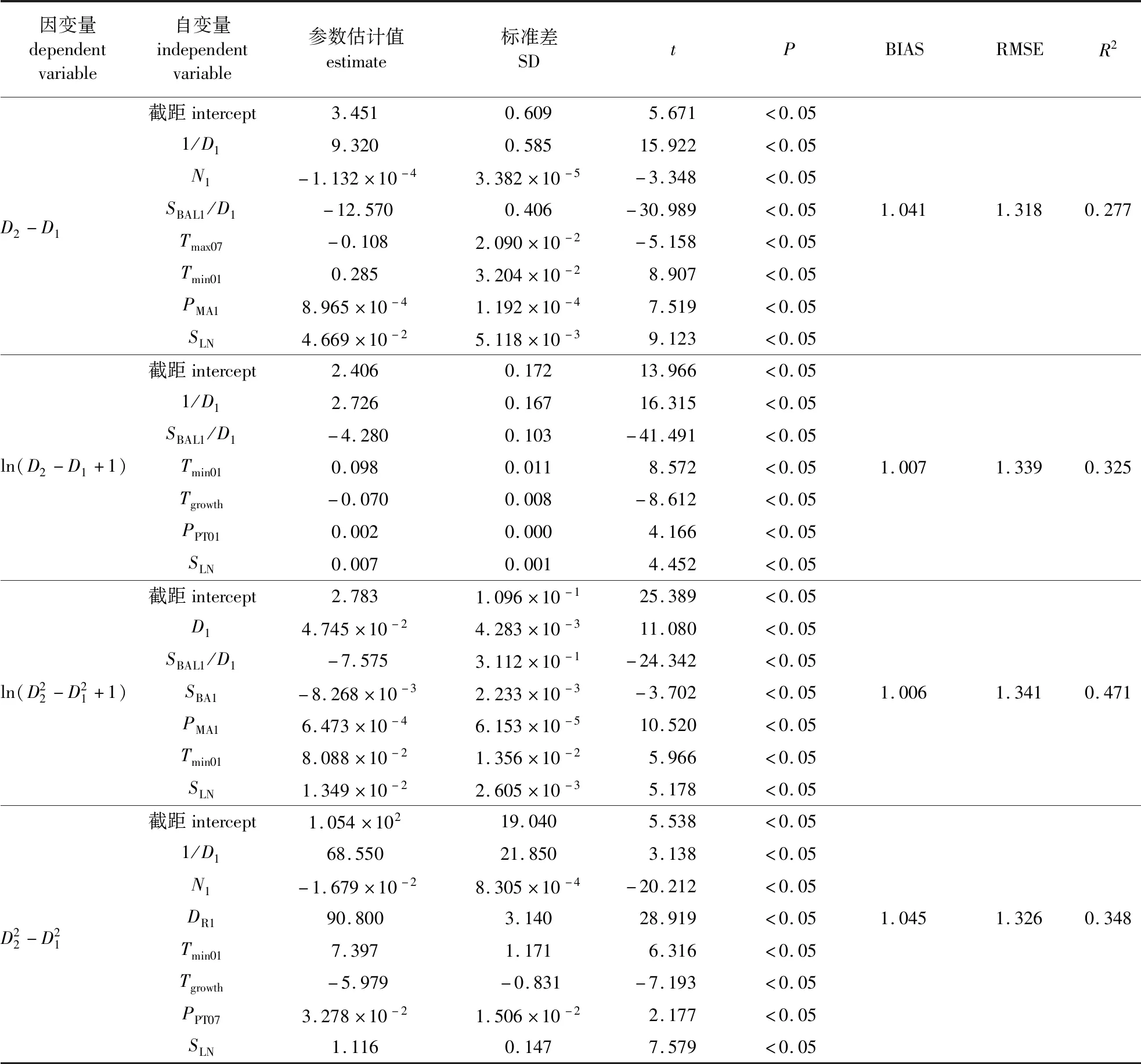
表3 不同因变量的杉木单木胸径生长模型拟合结果Table 3 The fitting results of Chinese fir individual-tree diameter increment models based on different dependent variables

综上所述，本研究最优基础模型形式如公式6所示。

(6)

其中：a0为模型截距，a1,a2,a3,…,a6为模型变量参数。

最优基础模型结果表明，D1、SBAL1/D1、SBA1、PMA1、Tmin01和SLN对杉木胸径的生长有显著影响，且变量之间的VIF值均小于5。基础模型的残差图和分位数-分位数图如图1所示。

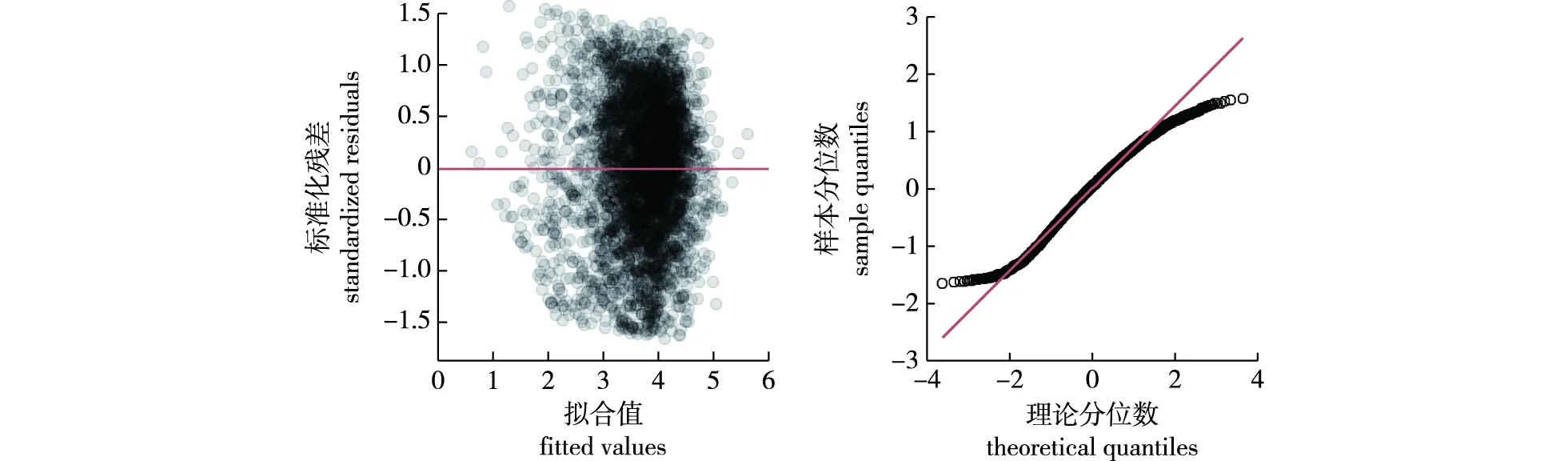
图1 最优基础模型残差图和分位数-分位数图Fig.1 Residual plot and quantile-quantile plot of optimal basic model

2.2 单水平线性混合效应模型

考虑到数据存在的异方差和自相关，本研究在最优传统模型的基础上引入了样地随机效应，构建单水平线性混合效应模型。

为确定模型的参数效应，在公式(6)的基础上，对127种不同随机效应参数的组合进行了模拟，其中拟合收敛的有66种，且不同参数组合有不同的拟合效果。根据AIC、BIC和-2LL越小越好的原则，筛选出随机参数个数相同时最优的模型，如表4所示。

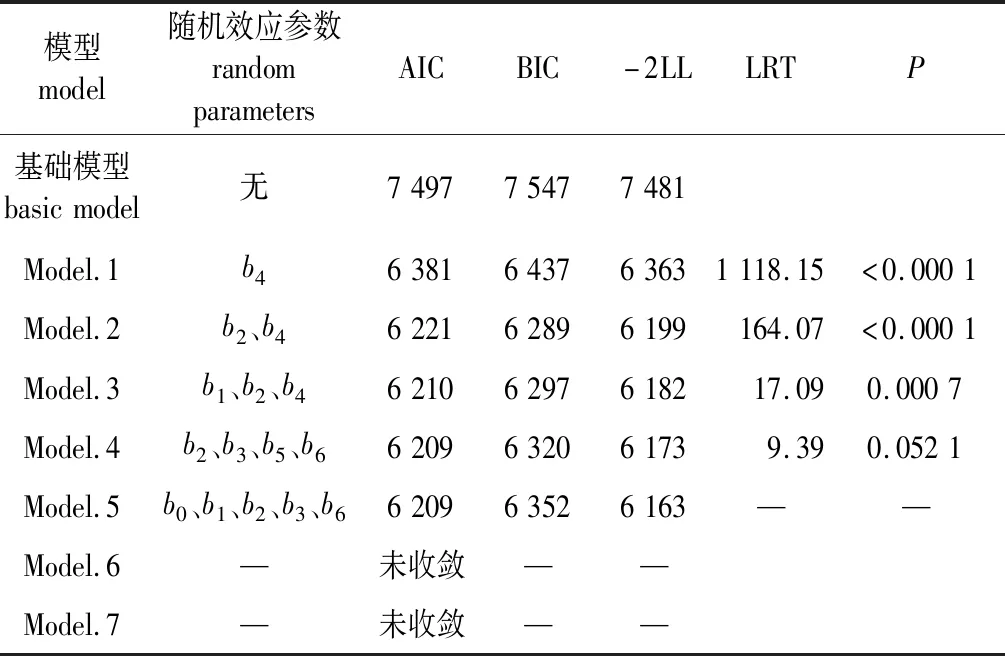
表4 杉木单木胸径生长混合效应模型随机参数组合的部分拟合结果Table 4 Partial results of combinations of random parameters for linear mixed-effects individual-tree diameter increment model for Chinese fir

由表4可以看出，与基础模型相比，随机参数的引入显著改善了模型表现。当随机参数从1个增加到4个时，模型的拟合效果越来越好，但是当随机参数增加到5个时模型的BIC变大，效果变差，随着随机参数进一步增加到6个和7个时模型拟合不收敛。为了防止过度拟合，对随机参数为1～4的模型进行了似然比检验，根据LRTs结果，最终当随机参数为3个时即Model.3拟合效应最好。Model.3具体形式如下所示。

(7)

其中：a0为模型截距，a1，a2，a3，…，a6为模型固定效应参数，b1、b2和b4为基于样地效应的随机效应参数。

在确定参数效应的基础上，引入了3种异方差函数(exponent、power和constpower)以及3种自相关结构来消除模型的异方差和自相关。模型拟合结果如表5所示。由表5可以看出，除复合对称结构未收敛外，异方差函数和自相关结构的引入均能显著提高模型的性能，评价指标有明显的改善。根据AIC、BIC、-2LL和LRTs，最终指数函数(exponent)和一阶自回归滑动平均结构[ARMA(1,1)]分别是消除异方差和自相关的最佳选择。

表5 基于不同异方差函数和自相关结构的混合效应模型比较Table 5 Comparison of mixed-effects models based on different variance functions and correlation structures

考虑了不同效应以及异方差函数和自相关结构之后，最终使用限制性最小二乘法(REML)获得的湖南杉木单木胸径生长混合效应模型结果如式(8)所示。模型的残差图和分位数-分位数图如图2所示，与基础模型残差图和分位数-分位数图相比，混合效应模型有所改善。

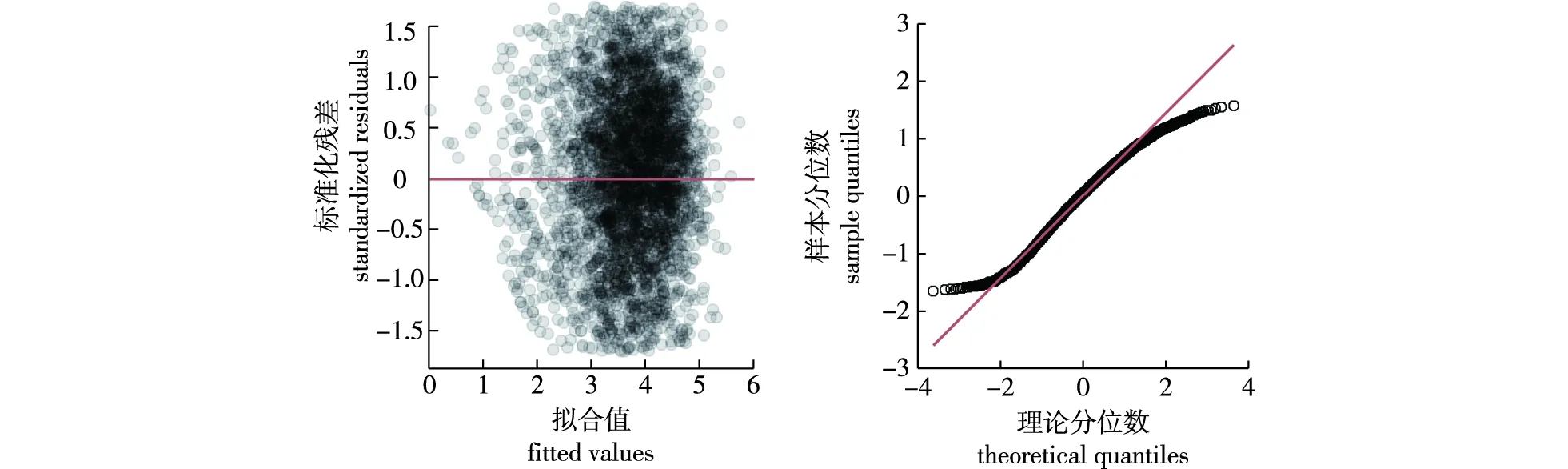
图2 混合效应模型残差图和分位数-分位数图Fig.2 Residual plot and quantile-quantile plot of optimal mixed-effects model

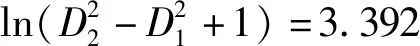
(8)

其中：

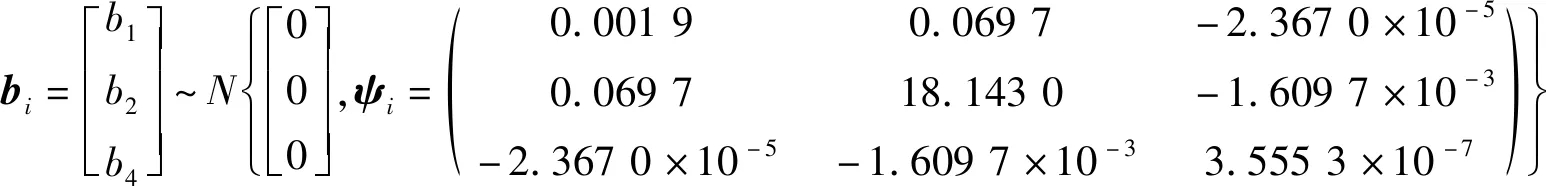
Ti=ARMA(1,1),ρ=0.909 3,v=-0.763 6。

2.3 模型检验结果

为了比较最优基础模型和混合效应模型的结果，对模型进行了进一步的检验和评价，模型检验结果见表6。可以看出，混合效应模型显著提高了模型的R2，减小了模型的AIC、BIC和-2LL值。似然比检验的结果表明基础模型和混合效应模型之间存在显著差异，混合效应模型结果更好。模型十折交叉验证的结果也证明了这一结论。此外，还绘制了基础模型和混合效应模型基于期末胸径的观测值和预测值散点图(图3)，结果表明混合效应模型预估精度更高。

表6 最优基础模型与混合效应模型的比较Table 6 Comparisons between optimum basic model and mixed-effects model

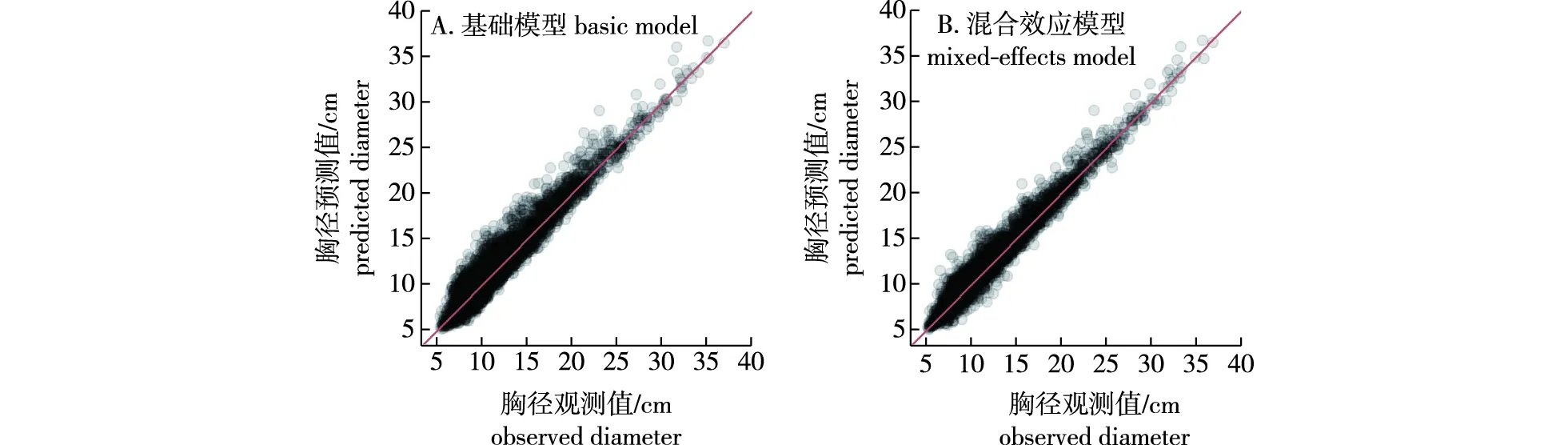
图3 基础模型和混合效应模型胸径观测值与预测值的散点图Fig.3 Scatter plots of the observed and predicted diameter (DBH) of the basic model and mixed-effects model

3 讨论

本研究表明：林木大小D1、竞争指数SBAL1/D1、立地条件SLN、其他林分因子SBA1以及气候因子PAP1和Tmin01对于湖南杉木单木胸径生长有显著的影响。

D1与胸径生长呈现正相关，这与很多研究结果相同[2,19,23]。主要是因为胸径较大的树木对光照、水分及土壤养分等资源有更强的竞争能力，因此胸径生长也要更快[24]。而事实上，胸径生长与林木大小的关系是单峰形式，即林木生长量在林木成熟时达到顶峰，随后生长趋于平稳，之后逐步下降。在本研究中未得到这一趋势，可能原因在于试验数据中的树木大多为幼龄和中龄林，处于快速生长时期。

SBAL1是一个与距离无关的单木竞争指数，反映林木在林分中竞争能力强弱，其值越大表明林木受到的竞争压力越大。SBAL1与胸径生长呈现负相关，即SBAL1越大，生长越慢，这与很多研究结果一致[25-26]。与林木大小对胸径生长作用的原理一样，SBAL1越大，对象木胸径越小，在林分中对于资源的获取处于劣势，树木的径向生长就会受到限制，生长速度比较慢。

SBA1是一个间接反映树木间竞争的指标，SBA1越大，说明样地内树木的竞争越激烈，树木的生长就会受到限制[2]。这也是在林分生长过程中需要进行间伐的原因之一。研究表明，间伐强度对胸径的生长有明显的促进作用。

在众多气候因子中，Tmin01和PMA1对杉木胸径的生长存在显著影响，并都对树木生长起到促进作用。可能原因是：一方面，最低温度的升高有助于休眠的结束，促进树木形成层提早活动，进而延长树木生长时间，促进树木的生长；另一方面，最低气温的回升可以促进地表温度的增加同时加速地面积雪的融化，增加降水，进而促进树木根部的活动，使林木生长加快[27-28]。对PMA1而言，树木生长的很多生理过程都需要水作为介质，比如光合作用所产生的碳水化合物在不同器官中的分配、矿质元素和无机营养物质的运输等，同时水还是树木某些代谢活动的原料和产物。因此，一般来说，年平均降水量的增加可以促进树木胸径的生长，二者呈现出正相关关系[28-30]。

在考虑坡度、坡向和海拔对于树木径向生长的影响中，坡向和海拔的组合对于杉木的生长呈正相关。对坡向(SASP)的研究结果表明树木阴坡生长量大于阳坡生长量，这与王建军等[19]和王向荣等[31]的研究结果一致。导致该结果的主要原因可能是由于样地位于我国南方地区，阴坡土层较深厚，光照充足，雨水充沛，更有利于杉木的生长。由此可以看出坡向对于环境资源的空间再分配以及林木的生长具有重要影响，在构建林木生长模型时需要将其考虑在内。海拔(SEL)的变化会造成温度、水分、土壤养分含量以及光照等诸多环境因子的差异，进而对林分生长产生较大影响。通常，高海拔地区的温度往往比较低，会导致林木生长季节较短，因而生长量就会较小，这与大多数学者的研究结果一致[19,23,32]。

由于林业数据常常具有重复测量和层次性的特点，不满足正态、独立、等方差的假设，采用传统的最小二乘法构建模型会产生有偏的标准差和预估区间[32]。因此，本研究引入了样地随机效应，构建了杉木单水平线性混合效应模型，提高了模型的预估精度。同时，还引入了异方差函数和自相关结构来定义模型的误差方差-协方差矩阵，解释随机误差的来源。与传统的基础模型相比，样地随机效应的引入明显改善了模型的表现，混合效应模型的决定系数由0.471 3提高到0.676 5，AIC和BIC分别减少1 535和1 479。混合效应模型十折交叉验证的评价指标NMSE和PRESS较传统的基础模型均显著减小，构建的模型具有较好的精度。