一种融合曲度的自适应八叉树点云压缩算法

甘斌

（西安市勘察测绘院，陕西 西安）

引言

随着激光扫描技术发展，三维点云的获取方法越来越多、精度越来越高。同时，数据量越来越大，其中也包含着大量的冗余点。冗余点对点云配准和模型重建过程中影响模型精度和效率，因此对点云进行简化压缩处理十分必要[1-4]。点云压缩是保留数据中的重要特征点，剔除一般冗余数据点。近年来，国内许多外学者对点云数据的压缩进行了研究，在一定程度上解决了点云冗余数据量大的问题。常用压缩方法主要是基于距离、角度、曲率、法向量等参数，采用网格、曲面拟合等方法进行点云数据的压缩[5-6]。Song 等[7]基于几何数据分析提出一种平滑点和边界点的区分方法，需预先进行数据平滑处理；Lan 等[8]将点云数据分配到均匀网格中，确定网格的中心点，通过中心点曲率与网格内其余点曲率对比，删除曲率差值小于曲率阈值的数据点，实现点云压缩，但存在压缩效率低的问题；庞卫峰等人[9]基于K 邻域拟合的二次曲面计算每一个点的平均曲率，以邻域区域内点的平均曲率中误差为阈值对点云进行简化压缩，压缩速度较快，但是压缩效果一般。采用点云抽稀和数理统计方法的点云抽稀压缩方法压缩速度较快，但是压缩效果一般；基于距离、提取中心等简单压缩算法普遍存在压缩过度、点云损失严重、导致模型失真等问题；基于曲率、法向量的压缩方法能够弥补简单压缩方法压缩过度的问题，但是存在压缩效率低、内存消耗大、压缩时间长等问题。

实验采用最优八叉树的分割方法对原始点云数据进行划分，保证八叉树叶子结点（立方体网格）内的点云数目合理，提高点云压缩的速度和质量。对点云数据进行曲面拟合，计算每一个点的最大曲率k1、最小曲率k2、综合曲率kp，进而计算曲度Cp[10-12]，根据网格内所有点的曲度分布情况确定压缩阈比ε，按比例阐述删除曲度值小的数据点，完成点云压缩，很好地解决了传统压缩算法在点云压缩的质量和速度问题，并通过实验进行分析与评价。

1 理论与方法

1.1 曲度

曲面的弯曲程度主要由曲率表示，曲率分为平均曲率、主曲率和高斯曲率。综合平均曲率和高斯曲率的相关特性，对两者进行综合利用，采用曲度来描述曲面的弯曲程度[10]。曲面中任意一点p 的曲度定义如下：

式中，Cp表示p 点的曲度，H（p）为曲面中P 点的平均曲率，K（p）为曲面中P 点的高斯曲率。

1.2 曲率计算

曲率计算主要包括平均曲率计算和高斯曲率计算，平均曲率指曲面中一点的两个主曲率的平均值，高斯曲率指曲面中一点两个主曲率的乘积。平均曲率和高斯曲率均反映曲面某一位置的弯曲程度。在本文中采用二次曲面拟合的方法进行点云曲率的计算，进而计算点云的曲度。局部点云二次曲面拟合及曲率计算方法参考文献[13、14]，计算步骤包括：确定局部曲面、计算高斯曲率K（p）和平均曲率H（p），计算方法如下：

二次曲面参数方程：

本文运用Yang[15]提出的二次参数曲面逼近法得到适合的二次曲面参数方程，令

二次曲面方程可表示为：

点云u、v 参数值可以由局部参数化方法求出，式（6）中a,b,c 的下标表示Q 中的行列号。通过最小二乘法，使邻域内个点到二次曲面的距离之和最小，推算出系数矩阵Q：

其中Z 表示该点的邻域矩阵。

求解计算二次参数曲面r（u，v）的偏导数ru，rv，ruu，rur，rvv曲面的单位法向量n 为：

1.3 自适应八叉树点云分割

八叉树是由四叉树在三维空间上扩展取得的，最早由Hunter 博士提出，八叉树结构可应用于多个方面，如空间物体分割、索引建立、金字塔模型构建等[16]。实验主要采用八叉树结构对点云数据进行空间划分，普通八叉树分割算法对点云数据进行分割，形成的子网格数目由递归深度决定，由于原始点云密度分布不均匀，在点云分割过程中容易形成网格中点云数目较少、甚至空网格，造成不必要的空间和时间的浪费。为解决这个问题，在普通八叉树的基础上提出自适应八叉树，根据网格内点云数目阈值停止八叉树分割，避免空网格的出现，如图1 所示，即当前网格点云数目小于点云数目阈值时停止该网格的继续分割，其它分支网格根据内部点云数目判断是否继续分割，进而建立一个基于点云数目的自适应八叉树，如图2 所示。

图1 普通八叉树与自适应八叉树对比

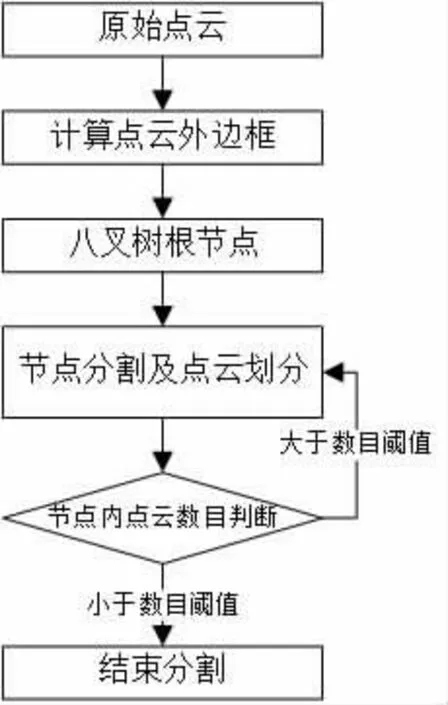
图2 自适应八叉树流程

1.4 压缩率

点云数据的压缩率R 表示去除的点云数目与原始点云数目的比值，公式如下：

R：压缩率；

N：原始点云数目；

Nk：表示压缩后剩余的点云数目。

2 压缩过程

实验采用曲度与八叉树相结合的方式进行点云数据的压缩，首先基于散乱点云的K 邻域进行曲面拟合，计算点云中每一个点的平均曲率和高斯曲率，根据曲度计算公式计算点云中每一点的曲度值。对点云数据进行最优八叉树分割，设置最小八叉树网格内点云数目阈值，当网格内点云数目小于阈值时停止八叉树分割，建立点云均匀分布的八叉树网格。最后对每一个叶子结点网格内的点云基于曲度值进行排序，根据用户输入的预计压缩比ε 删除网格内曲度值较小的点云，完成网格内点云压缩。最后遍历所有叶子结点，完成全部点云数据的压缩，如图3 所示。

图3 点云压缩流程图

3 实验分析

基于曲度的最优八叉树精简算法是基于散乱点云的曲度Cp和预计压缩比ε 进行点云数据的压缩。点云的曲度信息能够准确反应点云表面的特征信息，基于曲度的点云压缩能够提高点云的压缩质量，基于最优八叉树结构的点云压缩能够极大地提高点云的压缩速度，在保证压缩质量的前提下提高点云的压缩速度，将压缩质量与压缩速度完美结合。实验在Windows 平台上采用C++语言编写实现，计算机硬件配置为4G 内存、4 核3.30GHz 的intel 处理器。将本算法与Geomagic Studio 软件中的曲率压缩算法、栅格压缩算法和随机压缩算法进行对比分析。实验数据采用www.pudn.com 网站提供的兔子点云数据，兔子点云是经典的算法测试点云，共有35947 个数据点，采用本算法对兔子点云数据进行压缩，最小网格内点云数目阈值ε 设置为50，压缩比分别设置为0.1、0.3、0.5、0.8 时，压缩结果如图4（a、b、c、d、e）所示。采用Geomagic 软件的曲率压缩算法、栅格压缩算法和随机压缩算法进行兔子点云压缩处理，结果如图5 所示，压缩性能如表1 所示。

图4 本算法压缩结果

图5 Geomagic 压缩处理结果

表1 本算法与Geomagic 点云压缩性能对比

通过对图4 可以发现，点云的实际压缩率与预计压缩率成正比例关系，随着预计压缩率的增大点云的时间压缩率也逐渐增大。通过本算法对兔子点云压缩效果与Geomagic 软件中几种不同压缩算法的比较，在压缩率相同时，本算法的压缩效果比Geomagic 软件中栅格压缩算法和随机压缩算法的效果都好，基于曲度的压缩算法能够较好的保持点云的特征信息；压缩率相同时，压缩效果与Geomagic 软件中的曲率压缩算法相似，都能够很好的保持点云的特征信息，通过表1 可知在兔子点云的压缩过程中，由于本算法采用八叉树结构完成点云数据压缩，本算法比Geomagic 软件中的曲率压缩算法耗时更短，效率更高。

在时间压缩过程需要用户确定两个输入参数，即网格内点云数目阈值和预计压缩比，通过该参数的调整能够直接影响点云的压缩结果和压缩效率。采用唯一变量的实验方法，基于不同参数对兔子点云数据进行压缩，压缩结果与耗时统计如表2 所示。对结果进行统计分析，结果如图6、7所示。

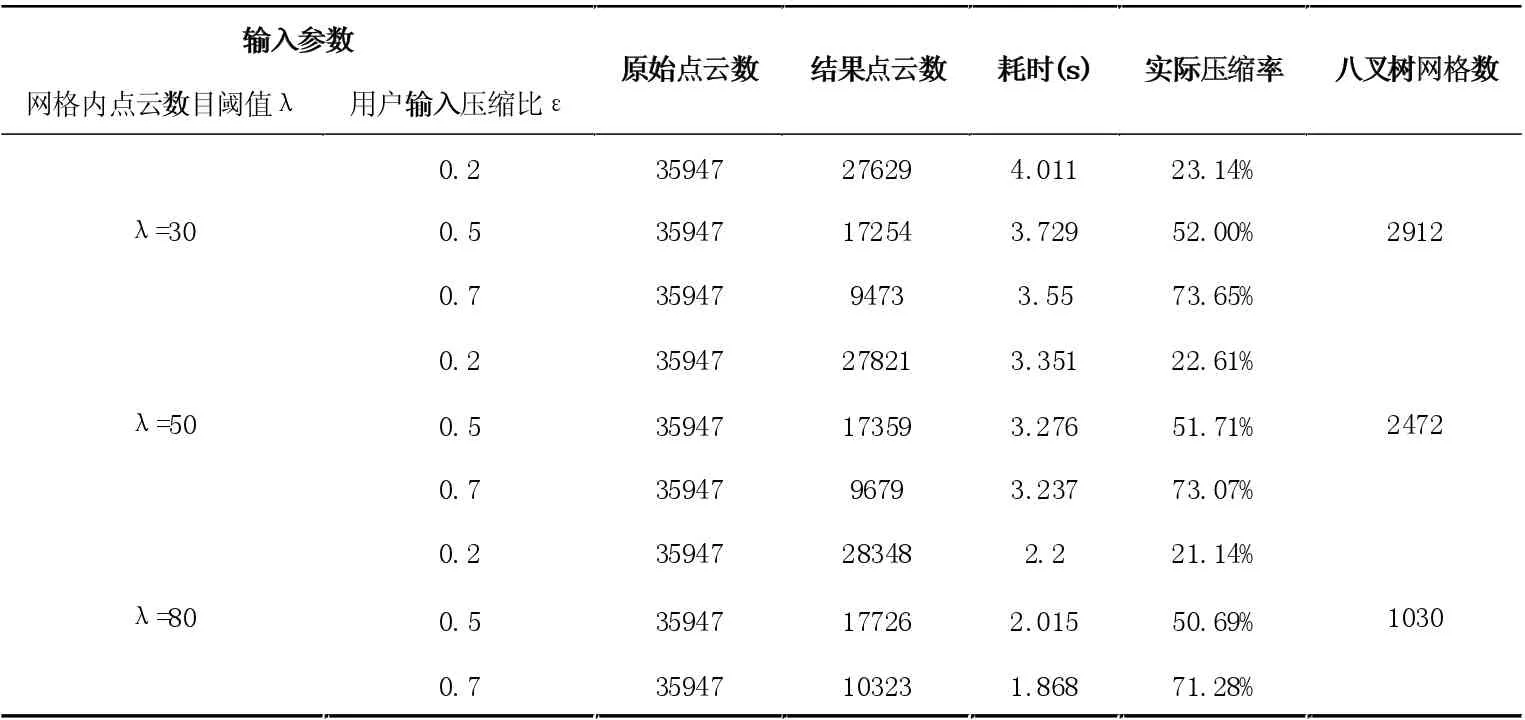
表2 不同参数点云压缩性能

在本算法中通过唯一变量的实验原则，在保持网格内点云数目阈值λ不变，更改预计压缩率ε的值逐渐变化，通过表2和图6 可以发现，随之预计压缩率ε 值得不断增大，点云的实际压缩率也不短增大，同时压缩时间逐渐减少；当预计压缩率ε不变时，随着点云数目阈值λ 的增大，实际压缩率与压缩时间同步逐渐增大。

图6 λ=50，点云压缩性能图

4 结论

图7 ε=0.5，点云压缩性能图

在曲率压缩的基础上进一步采用曲度作为评判标准进行点云数据的压缩，能够很好地保持点云的特征信息，保证良好的压缩质量；本算法基于八叉树的结构进行点云数据的抽稀压缩，能够基于八叉树的索引结构极大地提高点云的压缩效率，同时点云的八叉树索引结构对点云数据的存储、传输、以及其他应用具有一定的参考价值。本算法在程序性能上还能够继续优化改进，下一步研究将在算法实现的程序上进一步改进，从而提高点云的压缩效率和压缩速度。