基于平面补丁的自适应八叉树三维图像重建
2022-06-01马彩文
姚 程,马彩文
(1.中国科学院 西安光学精密机械研究所,陕西 西安 710119;2.中国科学院大学,北京 100049)
1 引言
三维图像重建是计算机视觉领域一个热门的研究方向。传统方法处理复杂形状的能力非常有限,需要花费大量时间和经历才能获得可接受的重建结果。随着三维数据规模的快速增长,借助机器学习的方法从大型三维数据集中学习形状空间,并通过学习到的特征进行三维图像重建已经成为一种发展趋势[1-4]。
基于机器学习的三维重建中,三维形状的表示是一个关键问题,它直接影响到学习网络的结构和生成三维图像的质量。目前,最常用的三维重建框架有稀疏体素表示,这种表示方式是基于二维图像的扩展,非常适合现有的深度学习框架[5-7]。然而,它存在数据存储量大、计算成本高的缺点,而且无法获得高分辨率图像。随着PointNet 的发展,三维点云表示成为用于形状分析和生成的表示形式[8]。但是,其输出质量受点数限制,并且从点云中提取高质量曲面需要额外的处理。作为计算机图形学中最常用的三维格式,多边形网格最近已用于基于学习的形状生成中,该方法可以通过使模板网格变形或找到2D 到3D 映射的神经网络直接预测表面补丁或网格[9-11]。但是,预定义的网格拓扑和模板网格的规则镶嵌生成的形状质量不高,尤其是对于不规则和复杂的形状[12]。
综上所述,在体素化一个三维空间中的模型时,需要对每一个存储信息的点求梯度,在计算过程中发现梯度不为0 的地方只存在于表面。因此,利用O-CNN 将计算限制在模型表面,但是重建出来的形体表面不够平滑。本文提出了一种基于自适应八叉树的卷积神经网络(Octree Convolutional Neural Network,CNN)。自适应O-CNN 基于一种以补丁为导向的自适应八叉树形状表示形式,该形式根据估计的简单补丁的近似误差,将体素自适应地拆分为八叉树所包含的局部形状。自适应O-CNN 的解码器可预测八叉树节点的占用概率,推导每个级别上每个非空八叉树节点的局部补丁,并分割其标签表面差的近似八叉树节点。它产生了一个自适应八叉树,在非空八叉树节点上的估计局部补丁是预测形状的多尺度自适应表示。除解码器外,还开发了一种用于自适应八叉树的高效3D 编码器,用于形状分类和3D 自动编码。
与现有的基于八叉树的CNN 相比,自适应O-CNN 继承了基于八叉树的CNN 的优势,同时将数据量为n3的问题简化为Cn2,在大量数据集进行训练的前提下,对于单图像进行同样规模的三维重建,存储效率高、计算成本低。
2 相关研究
3D 解码器是基于学习的形状生成任务的关键,可以根据其形状表示进行分类。
2.1 基于体素的解码器
布洛克等提出了基于体素的变分自编码器重构3D 形状,并使用经过训练的潜在代码进行形状分类[13]。Choy 等结合了3D 体积自动编码器的功能和长短期记忆技术,可从中重建体积网格单视图或多视图图像[14]。生成对抗网络被引入基于体素的形状生成和重构中,采用了不同的改善策略。然而,体素表示存在的分辨率较低的问题[15]。
2.2 基于稀疏体素的解码器
Häne 等提出基于八叉树的表示,它比形状预测的体素表示具有更高的效率和更高的分辨率[16]。Riegler 等在深度融合中使用基于八叉树的解码器[17],实现了2563甚至更高的分辨率输出。自适应O-CNN 则进一步提高了基于八叉树的CNN 网络的效率和预测准确性[18]。
2.3 基于点的解码器
Charles 等设计PointSetGen 用以从单个图像预测点坐标[19]。倒角距离和地球移动器的距离用作损失函数,以补偿预测值与真实物体之间的偏差。生成的点云近似于预期的形状。最近,Achlioptas 等改用GAN 技术来改善点云生成[20-21]。
2.4 八叉树技术
八叉树技术通过将三维空间细分为8 个八叉树节点来递归划分。它是许多计算机图形应用程序的核心技术,例如渲染、形状重构和碰撞检测。常用的八叉树的分割取决于内部形状,执行分割直到达到最大树深度为止,通常会均匀采样。由于形状信号在空间中分布不均匀,因此可以将自适应采样策略与八叉树集成在一起,进一步减小八叉树的大小。Frisken 等提出了基于八叉树的自适应距离场,在距离场包含精细细节的区域中保持高采样率,而在场平滑变化的区域中则保持低采样率[22-23]。本文提出的补丁引导自适应八叉树遵循此自适应原理,并使用局部补丁的拟合误差来指导分割。
3 基于补丁的自适应八叉树
本文引入了基于补丁的自适应八叉树。对于给定曲面S,从其外轮廓开始将三维图像分为8 个等大的立方体空间,对于八叉树节点O,将SO表示受八叉树细分立方体约束的S的局部表面。如果SO不为空,可以用一个简单的表面近似表示SO,本文选择最简单的平面来建立八叉树。依据式(1)建立与真实平面SO具有最小近似误差的最佳平面P。

其中:n是平面的单位法向量,d是平面的偏移量,P平面方程为:n·p+d=0,n∈R3。为了使法线方向与基础平面法线方向一致,核对n与SO的平均法线之间的角度是否小于90°,如果不是则将n和d同时乘以-1。
PO表示为受O所在的立方体区域约束的P的平面补丁。局部形状近似补丁的质量δO根据PO和SO之间的豪斯多夫距离确定,即:

式中disH(*,*)为求两个平面的豪斯多夫距离。豪斯多夫距离用于描述两组点集之间的相似程度,它是两个点集之间距离的一种定义形式。
改进后的八叉树划分规则为:对于任何不在最大深度级别的子节点O,如果SO不为空且δO大于预定义阈值,则对它进行继续细分,遵循此规则,可以生成补丁引导的自适应八叉树。所有非空子节点上的补丁对输入的三维形状进行了良好的近似,它们与输入形状之间的豪斯多夫距离以为阈值。的选取需要兼顾平面的近似效果、计算的复杂度和时间。如果阈值过小,计算的时间和复杂度会上升;如果阈值过大,则不能获得一个较好的近似平面。根据以上原则,逐步测试确定了最优阈值,即,其中h是八叉树中最长网络的长度。
基于平面补丁的自适应八叉树建立的三维模型如图1 所示。由于八叉树具有自适应性,平面补丁呈现不同的大小。为了更好地进行可视化,通过二维线性输入来说明三维自适应八叉树的原理,如图2 所示。很明显,二维自适应四叉树占用的内存要少得多,线段的集合可以较好地近似输入图形。由于存在近似误差,相邻非空叶八叉树节点的局部补丁之间是有缝隙的。为了填补这些空隙,可以采用表面重建和多边形修复技术。

图1 基于平面补丁的自适应八叉树建立的三维模型及在各层次上非空节点的自适应补丁Fig.1 Three-dimensional model based on plane patch-based adaptive octree CNN and non-empty leaf nodes of octree with adaptive patches at boundary layers

图2 二维自适应四叉树示意图Fig.2 Schematic diagram of two-dimensional adaptive quadtree
4 自适应八叉树神经网络
三维CNN 的主要组件包括编码器和解码器,对形状的生成及分类等任务至关重要[24-25]。由于八叉树和自适应八叉树的主要区别在于细分规则,八叉树的高效GPU 实现已直接移植到自适应八叉树上。
4.1 自适应O-CNN 的3D 解码器
基于八叉树的卷积神经网络是将稀疏信号表面存储在非空八叉树中,并将CNN 限制在八叉树内。在八叉树的每个层次中,每个八叉树节点都有其改组后的索引值。混合后的索引值按升序排序并存储在连续的数组中。给定一个八叉树节点的散乱键的索引值,可以计算出其相邻的八叉树节点的索引值,并检索相应的邻域信息,这对于实现高效的卷积操作至关重要。为了获得八叉树两个连续节点层次之间的父子对应关系,并标记出空的八叉树节点,通过一个索引数组记录八叉树的节点信息。在八叉树上常见的CNN 操作有卷积和池化,其计算方法类似于体素CNN。不过,基于八叉树的CNN 操作只在八叉树叶节点处进行卷积。从最下端叶节点开始计算,逐步向上进行CNN。当卷积操作的步长为1 时,数据以不变的分辨率处理,保持在当前的八叉树级别;当卷积操作步长大于1时,数据被压缩,沿着叶节点至父节点的方向压缩。
基于八叉树的编码器结构如图3 所示。将基于八叉树的卷积移植到基于自适应表面的八叉树三维编码器中。GPU 中自适应八叉树数据存储、卷积和池化操作与基于八叉树的卷积神经网络相同[26]。与八叉树不同,自适应八叉树输入信号出现在所有的八叉树节点处,而不仅仅是在最下端叶结点处;计算同时从不同层的叶节点开始,得到不同层的特征,最后组装在一起。

图3 基于八叉树和自适应八叉树的编码器网络Fig.3 Encoder network based on octree and adaptive octree
在基于八叉树的CNN 中,形状信息存储在最底层叶节点中,而基于自适应的八叉树则利用所有估计的局部平面作为输入信号。对于局部平面P(n·p+d=0,n∈R3)的l级八叉树的节点O,设置了一个四通道输入信号(n,)。这里c是O的中心点,d*=d-n·c,它与n·(x-c)+d*=0 是同一个平面方程。这里使用而不是d,因为受l级网格大小的限制,它是一个相对值,而d的范围很大,因为d是从原点到平面的距离。对于空的子八叉树节点,其输入信号设置为(0,0,0,0)。
自适应O-CNN 的3D 编码器将自适应八叉树作为输入,在八叉树的每一层,对这一层所有叶节点上的特征应用一系列卷积算子和ReLU,卷积核由这些八叉树节点共享。然后,通过池化将第l级处理过的特征下采样到第(l-1)级,并通过逐元素最大操作与第(l-1)级的特征融合。这些新特征可以进一步处理并与第(l-2)级、第(l-3)级的特征融合,直到最顶层。在实现中,最粗糙的级别设置为2,第2 级的八叉树节点强制为满,使所有特征都具有相同的维度。图3 为自适应O-CNN 3D 编码器架构。
4.2 自适应O-CNN 的3D 解码器
本文设计了一个3D 解码器来生成自适应八叉树,其结构如图4 所示。在每层八叉树,训练一个神经网络来预测每个八叉树节点的补丁近似状态——空的、表面良好近似和表面较差近似,并回归局部补丁参数,带有标签表面近似的八叉树节点会被细分,其中的特征通过反卷积操作传递给它们的子节点。当八叉树节点内的表面近似误差小于时,补丁形状可以近似真实表面,网络在这些八叉树节点处停止细分,并将它们作为当前八叉树级别的叶节点。以这种递归方式预测自适应八叉树,直到深度达到最大值。

图4 自适应八叉树CNN 解码器结构Fig.4 Structure of Adaptive octree CNN decoder
预测模块中,用于预测的神经网络由“FC+BN+ReLU+FC”操作组成。其中,BN 代表批标准化,FC 代表全连接层。该模块在自适应八叉树的同一级别的所有八叉树节点之间共享。预测模块的输出包括补丁近似状态和平面补丁参数(n,)。通过补丁近似状态来确定八叉树是否需要细分,同时也用于计算八叉树的反卷积算子。
自适应O-CNN 解码器的损失函数包括结构损失和补丁损失。结构损失Lstruct测量预测的八叉树结构与其真实值之间的差异。由于八叉树节点状态是3 类分类,使用交叉熵损失函数来定义结构损失。将Hl表示为八叉树l层的交叉熵,结构损失是所有层交叉熵的加权和,即:

式中:nl是预测八叉树第l层的八叉树节点,lmax是最大深度,wl是每个层定义的权重。与编码器类似,八叉树的最顶层是2 并且充满了八叉树节点,所以l从2 开始。这里将wl设置为1。Lpatch测量每个级别中所有子八叉树节点的平面参数和实际物体之间的平方距离误差,即:

式中:ni和是预测参数和是真实值'是预测八叉树第l层的子八叉树节点,λ设置为0.2。当八叉树级别超过4 时使用自适应八叉树,因此l的初值设为4。对于在真实数据中不存在的错误生成的八叉树节点,它们没有补丁损失,仅考虑结构损失。
由于预测平面应该通过八叉树节点,否则违反了平面块在八叉树节点内的假设,这里添加约束|d*|<。式中,hl是l级八叉树节点的网格尺寸。
5 实 验
5.1 自动编码器
自动编码器技术能够学习输入图像的紧凑表示,并通过解码器从潜在代码中恢复信号。本文采用自适应O-CNN 编码器和解码器来形成3D 自动编码器,在GTX 1080,8 G 内存的条件下进行测试。在ShapeNet Core v2 数据集上训练了该3D 自动编码器,其中包含来自13 个类别的39 715 个3D 模型[6,27]。训练和测试拆分规则与AtlasNet 中使用的规则相同。自适应八叉树的最大深度为7,即体素分辨率为1283[28]。
通过测量3D 模型与其真实形状之间的倒角距离来评估解码形状的质量。表示真实点云,神经网络预测的点,Sg和S之间的倒角距离定义为:

因为3D 自动解码器输出一个补丁引导的自适应八叉树,为了计算倒角距离,从估计的平面补丁中均匀地采样一组密集点。首先,将包含在自适应八叉树的非空叶节点中的平面补丁细分为1283的分辨率,然后在每个细分的平面块上随机采样一个点,形成输出点云。对于真实的密集点云,也在1283的分辨率下进行均匀采样。
质量测量结果如表1 所示。本文还与两种最先进的3D 自动编码器方法进行了比较,其中AtlasNet 生成一组网格补丁作为形状的近似值,PointSetGen(PSG)生成点云输出。与预测125个网格块的AtlasNet 相比,自适应O-CNN 自动编码器实现了最佳质量。需要注意的是,本文应用的评价标准为倒角距离,AtlasNet 的损失函数就是倒角距离,而自适应O-CNN 自动编码器的结构损失函数和补丁损失函数并没有用到此函数,仍然取得了较好的成果。与PSG 相比,自适应O-CNN 和AtlasNet 的质量要好得多。

表1 三维自动编码器质量Tab. 1 Three-dimenslional autoencoder quality
自适应O-CNN 在某些类别中的表现比AtlasNet 差,例如飞机和椅子,如图5 所示。在这些类别中模型相对较薄的部分,例如飞机的机翼、椅子的扶手以及枪管,自适应O-CNN 与原始形状有较大的几何偏差。AtlasNet 的偏差较小,但它用单个补丁或凌乱的补丁来近似部分实体,有的结构完全丢失,很难甚至不可能定义这些区域的内部和外部。相反,自适应O-CNN使用基于八叉树的结构损失和补丁损失进行训练,具有更好的效果。

图5 三维自动编码器测试结果Fig.5 Three-dimenslional autoencoder results
3D 自动编码器可用于恢复几何形状的缺失部分并处理输入噪声。这里进行了一个形状完成任务来证明自适应O-CNN 的有效性。从ShapeNet Core v2 数据集中选择汽车类别作为地面实况数据。每辆车随机选择3 到5 个视图并从这些视图中采样密集点。在每个视图上还随机裁剪一些区域以模拟孔洞,并略微扰动点位置以模拟扫描噪声。这些视图组合在一起作为不完整和嘈杂的数据。在这个合成数据集上训练了基于自适应O-CNN 的自动编码器,以不完整的形状作为输入,以相应的完整形状作为目标。作为参考,还在该数据集上训练了基于O-CNN 的自动编码器。所有网络中八叉树的最大深度设置为7。自适应O-CNN 的结果更接近真实情况,而八叉树卷积神经网络却未能填补一些漏洞。
5.2 从单个图像重建形状
从2D 图像重建3D 形状是计算机视觉和图形学中一个重要的课题。随着3D 深度学习技术的发展,从单个图像推断3D 形状的任务在研究界引起了广泛关注。这里对自适应O-CNN 的这项任务进行了实验,并与最先进的方法进行了比较,即AtlasNet 和PointSetGen(PSG)[8,19,28],真实3D 形状来自ShapeNet Core v2,每个对象都是从24 个视角渲染的,背景是透明的。在与OctGen进行比较时,由于OctGen 仅在具有1283分辨率八叉树的汽车类别上进行了训练,因此自适应OCNN 也在具有相同分辨率的汽车数据集上进行了训练。测试在GTX 1080,8G 内存的条件下进行。对于图像编码器,AtlasNet 使用了ResNet18,OctGen 使用了经典的LeNet。
实验得到了预测点与从PointSetGen、Atlas-Net 的原始网格采样的点之间的倒角距离,如表2所示。Groueix 等随机选择了260 个形状(每个类别20 个)来形成测试数据库[8]。为了与PointSet-Gen 进行比较,他们运行了ICP 算法对齐来自PointSetGen 和AtlasNet 的预测点与真实物体点云。注意ICP 对齐后,倒角距离误差略有改善。此外,还运行了ICP 算法来使自适应O-CNN 编码器的结果与真实情况保持一致。我们的方法在13 个类别中的8 个类别上实现了最佳性能,特别是对于具有大平坦区域的对象。单图像三维重建的测试结果见表2,表中的数值为倒角距离乘以1 000。如汽车和橱柜,自适应O-CNN 的输出在视觉上更平滑。对于图6 最后一行的翻盖手机图像,所有方法的重建质量都相对低于其他输入图像,因为翻盖手机在训练数据集中是很少见的。
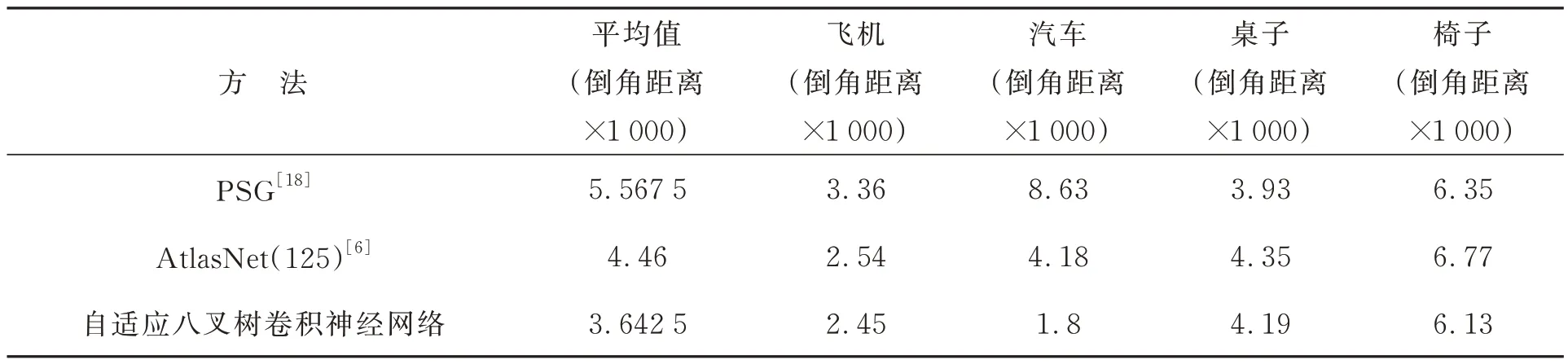
表2 三维重建测试结果Tab. 2 3D reconstruction test results(The Chamfer distance is multiplied by 1000)
为了计算OctGen 输出的倒角距离,从边界八叉树节点中密集采样点进行评估。基于面片的自适应O-CNN 具有比OctGen 更低的倒角距离误差,两者分别为0.274 与0.294。三维重建视觉结果如图6 所示。与OctGen 相比,自适应O-CNN 能够保留更多的结构细节,生成的表面补丁更接近于实际形状,尤其是较为平整的区域。

图6 三维重建测试结果Fig.6 Three-dimencional reconstruction test results
6 结论
本文提出了一种用于3D 编码和解码的自适应O-CNN,其编码器和解码器继承了补丁引导的自适应八叉树结构的自适应性和重建质量。在典型的3D 学习任务(包括3D 自动编码以及图像的表面预测)上,与包括基于八叉树的CNN 等先进的方法相比,基于平面补丁的自适应O-CNN 不仅减少了内存和计算成本,而且具有更好的形状生成能力。单个图像的形状预测结果验证了自适应O-CNN 的效率和有效性,倒角距离误差为0.274,低于OctGen 的倒角距离误差0.294,重建效果更好。
