暂态电路层次性Proteus虚拟仿真分析

李谊萍，刘锋华，詹华群

(1. 江西农业大学南昌商学院，江西 九江 332020；2. 江西科技师范大学通信与电子学院，江西 南昌 330013)

1 引言

现代科学技术的飞跃式进步，虚拟现实技术的不断完善，使得虚拟实验模式[1]得以大力推广。该模式通过融合虚拟现实技术[2]与多媒体信息技术，虚拟化处理实验的环境、对象、过程与结果，在计算机硬件的支持下，广泛应用于各个领域。

虚拟仿真模式作为计算机技术推动科学实验发展的必然产物，不仅表现形式直观，而且能从根本上去除真实实验中潜在的风险与安全威胁。本文将其融入电力领域的科研探索中，基于Proteus软件，构建出适用于暂态电路的多层次虚拟仿真模型，以更好地促进电力行业向高水平的数字化、智能化方向发展[3，4]。暂态电路的结构与参数通常会发生动态变化，想要较好地完成虚拟仿真的难度较大，为此，本文尝试通过以下几种手段，取得更理想的暂态电路虚拟仿真效果：借助Proteus软件的混合仿真模块与虚拟系统仿真模块优势，结合电力系统分析综合程序特点，提升暂态电路仿真与动画效果的真实度与响应速度，实现实时的交互式仿真，帮助用户直观地看到实验过程与分析结果；利用贝叶斯分类法，将虚拟仿真内容按用户需求划分为多个层次，有助于满足不同用户对电路的设计与研究需求。

2 暂态电路分析

暂态电路结构动态变化的过渡阶段是虚拟仿真的实现难点与关键点，因此，建立以电流为变量的微分方程，以更合理地分析过渡过程中蕴含的动态变化规律[5]。令基于正弦激励作用[6]的电路电流与电压呈相同指数规律进行动态变化，换路阶段的电感电流不存在跃变现象[7]，故初始的电感电流IL0由下列计算公式解得

(1)

其中，Us指代电源电压；{R1，R2，…，Rk}指代电路上的k个电阻。

根据基尔霍夫电流定律[8]与基尔霍夫电压定律，利用下列方程组描述电流与电阻之间的关系：

(2)

当电路呈稳态时，电感呈短路状态，则稳态条件下电流与电阻的关系式如下所示

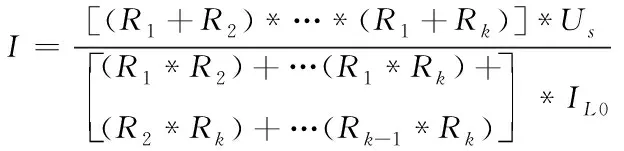
(3)

其中，基于电感L的等效电阻计算公式如下所示

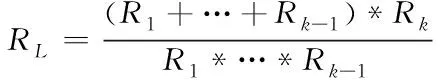
(4)

由此推导出时间常数τ的计算方程式

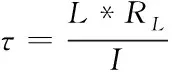
(5)

结合以上公式，建立出以电流为变量的暂态电路微分方程，如下所示

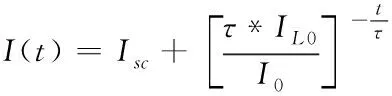
(6)

该式反映出t时刻下电路的暂态情况。其中，Isc、I0分别指代等效电源电流与初始电流。

3 层次性虚拟仿真模型构建

3.1 Proteus虚拟仿真模型架构

利用智能原理图输入系统、混合模型仿真器、动态器件库、高级图表仿真单元、高级布线编辑工具、虚拟系统仿真模块、印制电路板设计模块等部分构成的Proteus嵌入式电子设计自动化工具软件[9]，结合电力系统分析综合程序软件[10]，构建出图1所示的虚拟仿真模型。

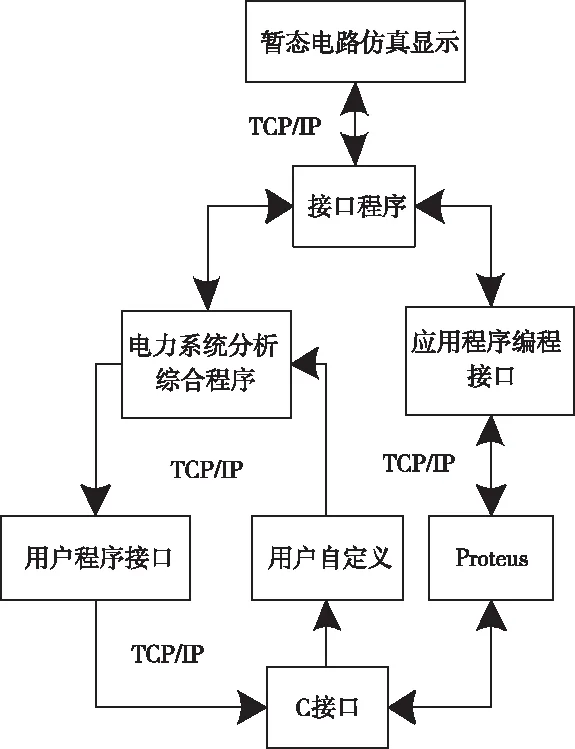
图1 虚拟仿真模型架构示意图

电力系统分析综合程序软件与Proteus软件的具体运作流程描述如下：

1)Proteus利用直接编程接口[11]启动暂态运算指令，通过暂态仿真计算获取边界等值参数；

2)将解得的边界等值参数经C接口传输给电力系统分析综合程序；

3)电力系统分析综合程序由用户自定义模块获取边界等值参数，利用该软件自带的暂态运算应用程序展开仿真计算；

4)所得边界等值参数反馈给电力系统分析综合程序后，通过用户程序接口与C接口发送至Proteus，根据两次计算结果进行误差修正；

5)经应用直接编程接口与接口程序，传输最终的边界等值参数运算结果到仿真显示平台。

令Proteus数字模型中含有的电路状态与实际暂态电路常见的九种状态一一对应，提高虚拟仿真的真实性、合理性，以更好地完成暂态分析。具体内容设置如表1所示。

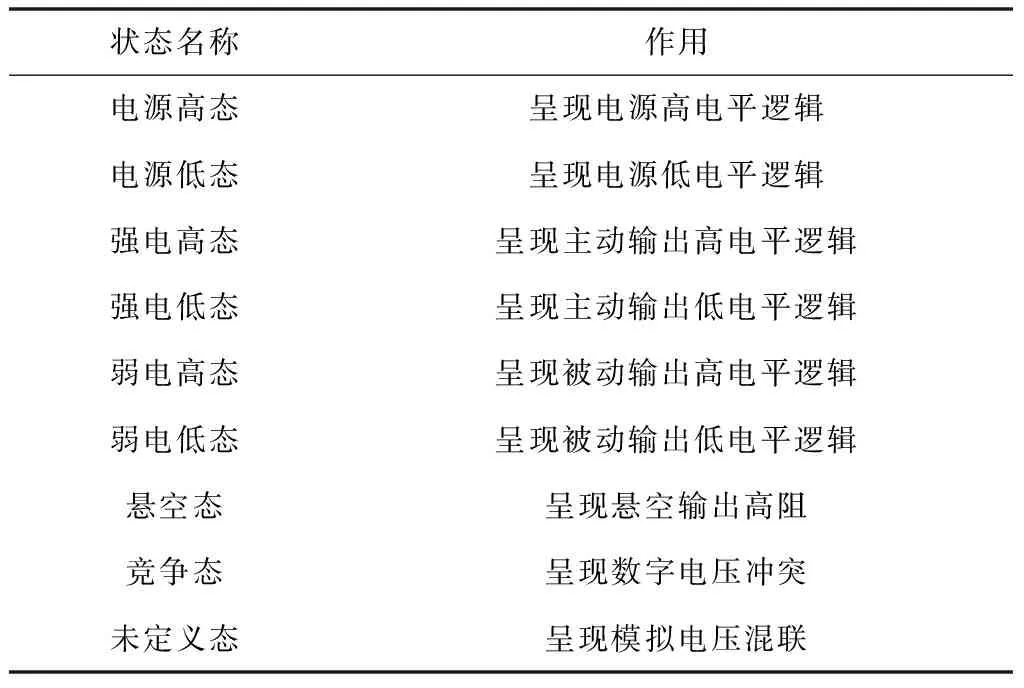
表1 Proteus数字模型暂态电路状态设置

模型中提及的Proteus软件暂态仿真算法，是针对暂态电路的数学分析结果提出的。离散化电路元件[12]，利用下列一阶线性方程界定t时刻下各元件的输出信号yι(t)

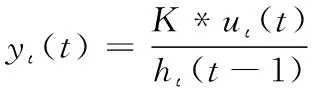
(7)

其中，uι(t)指代第ι个元件t时刻的输入信号；hι(t-1)表示该元件t-1时刻的历史信号；K指代离散系数。

由此推导出九种状态下各元件的输出信号方程式，如下所示

(8)

3.2 虚拟仿真内容层次划分

根据暂态电路的数学分析与Proteus虚拟仿真模型结构，利用朴素贝叶斯分类法[13]，将虚拟仿真内容按用户需求划分为多个层次，满足不同用户对电路的设计与研究需求。虚拟仿真内容划分流程具体如下所述：

1)已知与电路相关的数据样本个数是n，每个数据均带有N个属性，数据集合为X={X1，X2，…，Xn}，属性集合为A={A1，A2，…，AN}；

2)设定数据集的初始类别个数为m，类别集合为C={C1，C2，…，Cm}，则对于未知数据x∈X，根据下列表达式进行类别划分：

P(Ci∣x)≥P(Cj∣x)

(9)

该式表明，数据x划分至第i个类别中的后验概率P(Ci∣x)不小于分类至第j个类别的后验概率P(Cj∣x)。其中，i≠j=1，2，…，m。

3)基于朴素贝叶斯理论[14]，通过下列方程式求解出数据x划分到类别Ci的后验概率P(Ci∣x)

(10)

其中，P(x)指代数据x的先验概率；P(x∣Ci)表示相对于类别Ci的数据x似然度；P(Ci)、P(Cj)分别指代类别Ci与Cj的先验概率。

4)为减少运算开销，令数据属性互不相关且具有连续值特征，则属性集合A={A1，A2，…，An}服从高斯分布。利用均值是μ、标准差是σ的高斯分布函数g()，更新数据集合X={X1，X2，…，Xn}的类别个数m，得到最佳聚类数m′，即根据用户不同需求划分的虚拟仿真内容层次个数。基于高斯分布函数的更新公式如下所示：

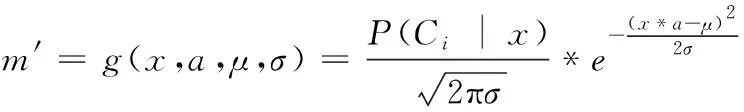
(11)

其中，a指代数据的任意属性，a∈A；e()指代欧拉函数[15]，用于修正层次划分偏差。

4 暂态电路层次性虚拟仿真效果分析

4.1 实验环境搭建

选用Proteus VSM 8051版本仿真软件，搭建虚拟仿真模型及运行环境。设定仿真步长与总时长分别是0.05s与1s。针对某电力设备的回路元件分布形式，按照表2中的元件参数，建立出用于虚拟仿真的暂态电路模型。

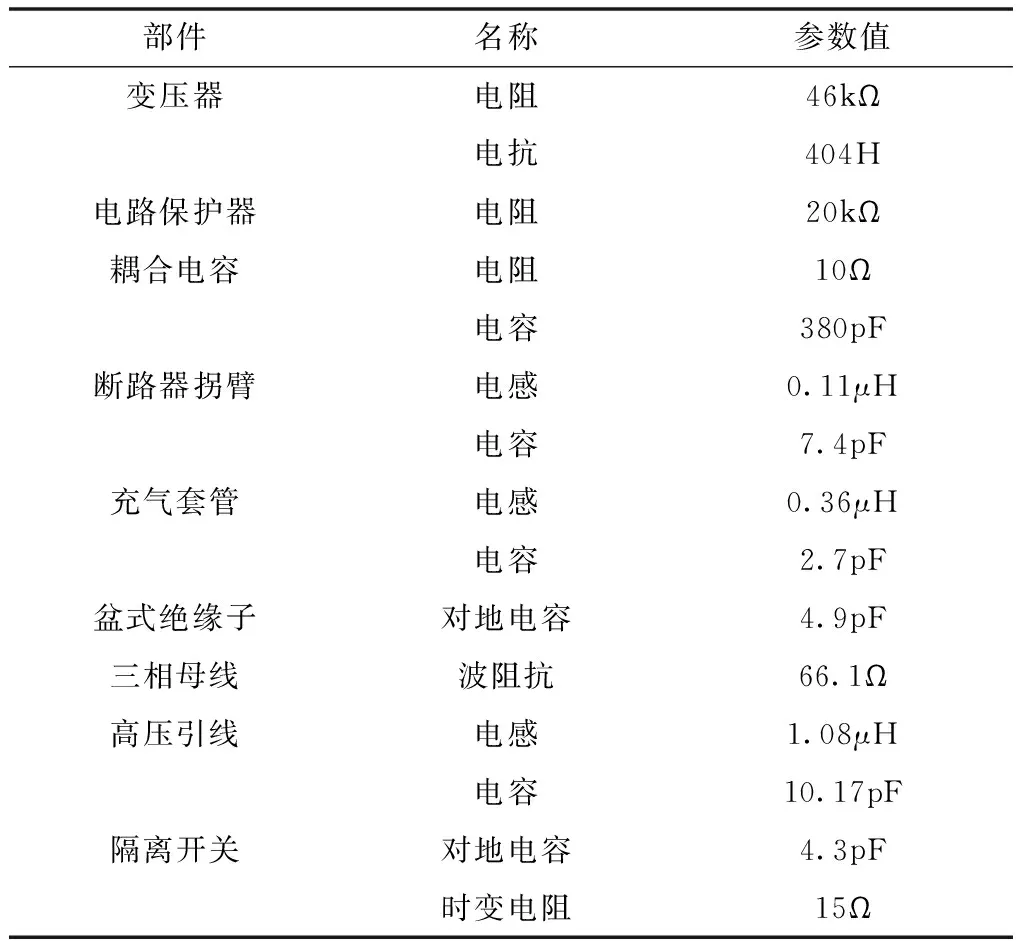
表2 暂态电路模型中各元件参数

4.2 暂态电路虚拟仿真有效性

图2所示为虚拟仿真模型构建的目标暂态电路模型。

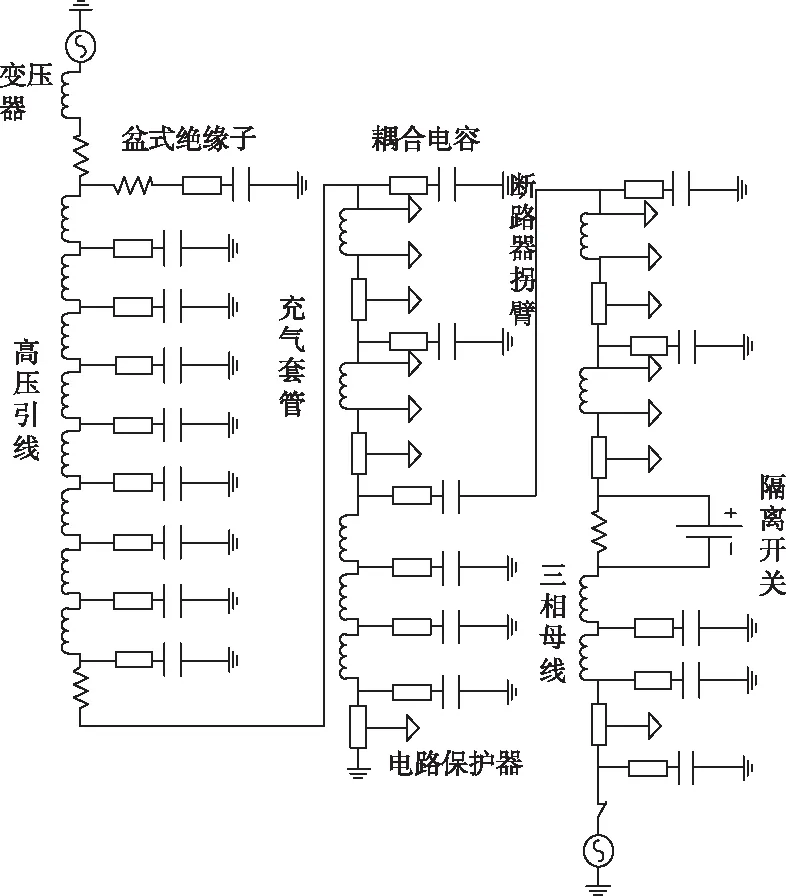
图2 暂态电路虚拟仿真模型示意图

从Proteus仿真图中展示的电路情况可以看出：本文借助Proteus软件的混合仿真模块与虚拟系统仿真模块优势，令Proteus数字模型中含有的电路状态与实际暂态电路常见的九种状态一一对应，细致地显示出设备电路中所有元件与连接细节，不仅能满足用户建立暂态电路时对虚拟工具与仪器的需求，而且具备一定的动态仿真能力，能让用户清楚地看到元件参数变化时电路的暂态变化过程，更容易掌握电路中各元件的运行特点，为开展下一阶段的研究提供参考依据。

4.3 层次性虚拟仿真准确性

为检验层次性虚拟仿真模型的精准度与可靠性，探索模型的影响因素，令放电电压相一致，断路器断开后动、静触点的间距[16]分别为5mm、10mm，设定母线在0.35s时分别发生单相接地[17]与三相接地的0.11s时长故障。图3和图4分别为5mm开距下和10mm开距下电路暂态电压波形示意图。

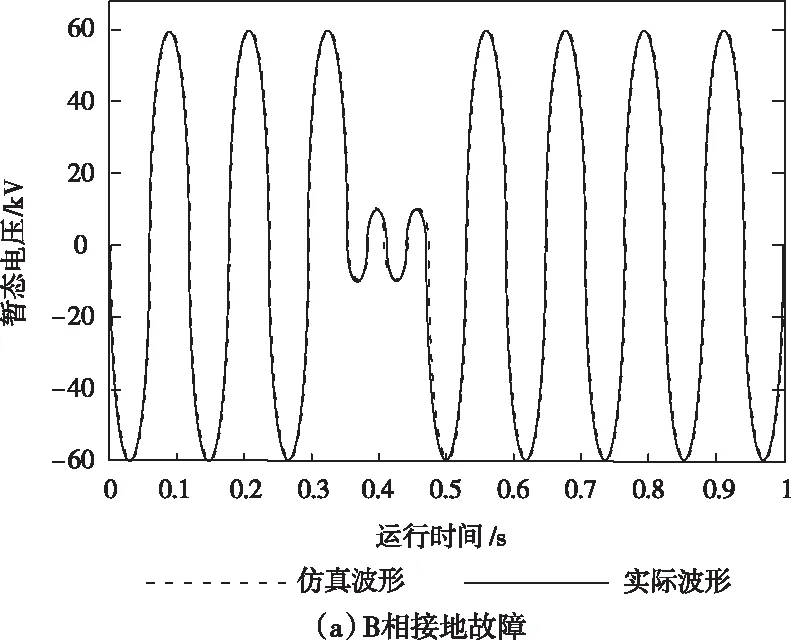
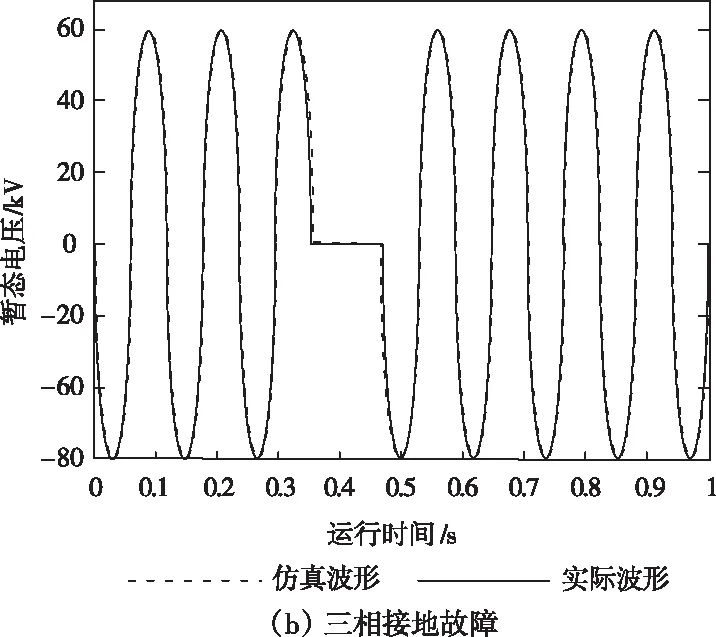
图3 5mm开距下电路暂态电压波形示意图

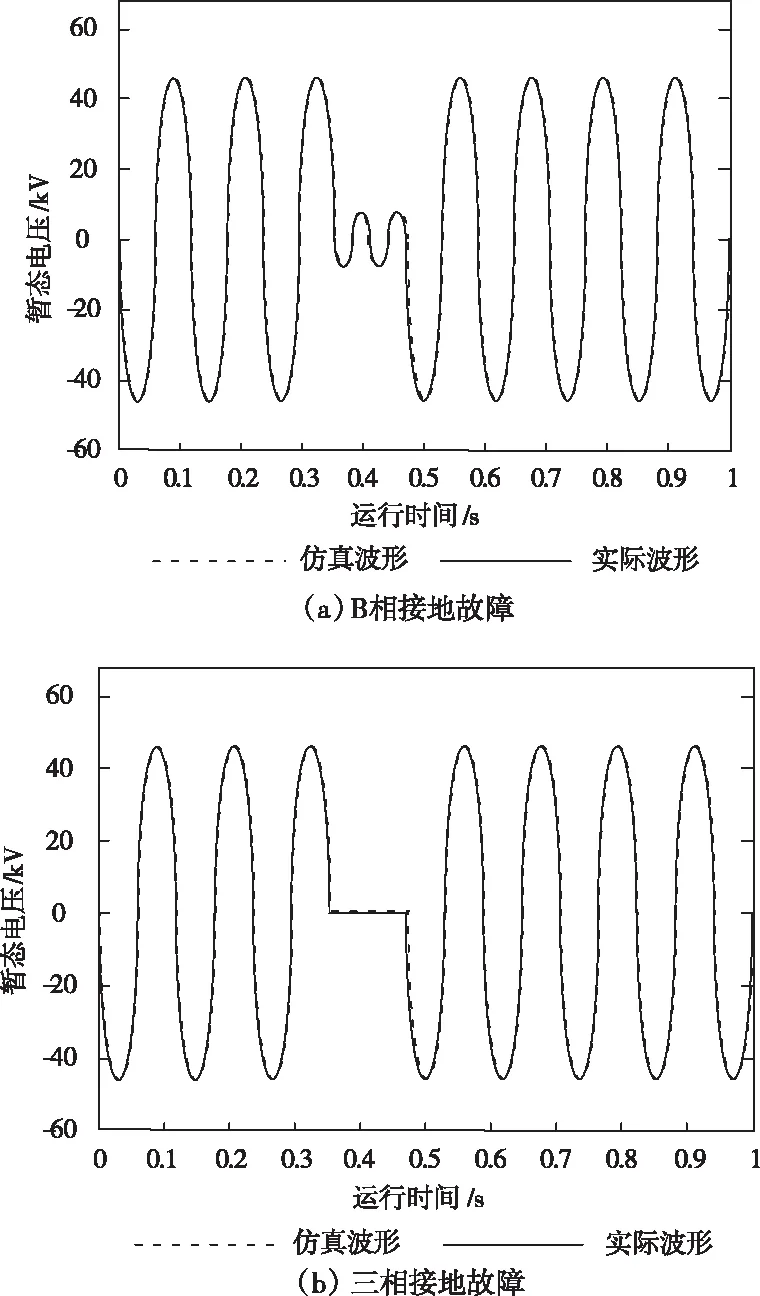
图4 10mm开距下电路暂态电压波形示意图

通过对比5mm开距下两接地故障的电路暂态电压模拟与实际变化波形拟合情况(如图3所示)可以看出：模拟波形与实际波形重合度较高，准确呈现出0.35s时发生的B相接地故障与三相接地故障。

根据10mm开距下两接地故障的电路暂态电压模拟与实际变化波形拟合情况(如图4所示)可以看出：两个波形的趋近程度较高，且故障种类的表现形式明显；相较于5mm开距的波形趋势，10mm开距的暂态电压波形除升降幅度有所减小外，整体变化走势基本一致，且缩减幅值并不影响对电路暂态的分析。

综上所述，本文根据基尔霍夫定律，联立电流与电阻关系，以电流为变量，建立暂态电路微分方程，能较好地抑制开距干扰，有效完成不同故障下暂态电路的虚拟仿真，并取得准确、可靠的仿真结果，令波形变化趋势与故障时长，与实际情况高度吻合。

5 结论

计算机技术与网络技术的飞速发展，使得虚拟仿真技术与多媒体信息技术不断升级，并有效融合，衍生出一种新型的虚拟仿真形式。该实验模式打破了传统实验形式的重重限制性壁垒。当前暂态电路的虚拟仿真精准度较低，无法满足现代电力领域的仿真需求，因此，本文以Proteus软件为基础，设计出具有层次性的虚拟仿真模型。尽管现已取得阶段性的研究成果，但为了加强模型的通用性，下一步将就以下几个方向展开优化：创建可扩展的数字式数据库，以便于后续补充电路相关数据；应利用组态形式整合所用软件，完善软件性能，提高模型兼容性。