基于网络演算的无线Mesh网时延上界
2023-03-29魏德宾颜佐任
魏德宾,程 健,杨 力,颜佐任
(1. 大连大学通信与网络重点实验室,辽宁 大连 116622;2. 大连大学信息工程学院,辽宁 大连 116622;3. 南京理工大学自动化学院,江苏 南京 210094)
1 引言
无线Mesh网(Wireless Mesh Networks,WMNs)作为一种宽带接入技术,与传统无线网络相比,它具有节点移动灵活、接入方式多样等优势,近些年备受研究人员关注[1]。该网络主要由三层构成,分别是Internet接入层、核心网层和输出接入层。核心网层介于Internet接入层与输出接入层之间,是影响WMNs性能的关键,针对核心网性能的分析将为WMNs架构设计、网络优化等带来参考。
端到端时延是分析研究核心网网络性能的重要指标,也是衡量网络服务质量(QoS)和用户体验的重要参数,时延上界的求解对WMNs的发展和应用具有现实意义。它主要受到链路上各节点的服务延迟、链路节点个数、调度策略、网络拓扑、流量分配方式等综合因素的影响。端到端时延上界分析的准确性直接影响到网络QoS保障水平,同时也是网络接纳控制、路由优化的重要依据。
网络演算(Network Calculus,NC)是一种有效计算端到端时延上界的数学工具,很多学者对此进行深入研究。文献[2]基于NC理论对单、多两种节点形成两种不同的到达和服务曲线模型对时延上界进行紧致计算评估。李庆华等人[3]针对无线自组网,基于已存在的链路吞吐量模型,运用网络演算计算了节点的端到端时延上界、时延抖动上界等结果。陈志刚等人[4]利用网络演算理论,通过模拟实验和数值分析,对无线多跳网进行推导,从而确保了无线多跳网络的QoS,从而证实了理论结果的正确性。文献[5]从降低端到端时延上界的计算复杂度角度出发,提出LAC(Loacl Arrival Curve)组合分析方法,但是此方法计算的时延上界紧密度却低于NC理论。在新型应用上,文献[6]利用随机网络演算,推导了物联网业务流的到达曲线和服务曲线,求解了机器业务流的端到端时延上界。文献[7]运用NC对软件定义车联网(SD-IoV)中传输数据建立模型并引入遗传算法,最终设计出符合SD-IoV的路由算法进行路径传输。文献[8]针对5G蜂窝移动通信技术中的云无线接入网,对不同优先级的业务流计算了其端到端时延及数据积压上界。文献[9]研究了卫星5G一体化网络中各组件之间连接关系的串联模型,并基于该模型给出了端到端延迟计算函数。
无线Mesh网的早期考虑到网络易于管理和配置,主要使用单径传输。但由于通信需求的增加,单径传输易导致流量集中在某条路径形成“热线”,端到端时延会变得很大。多径传输[10]可规避形成单路径“热线”情况,降低网络端到端时延,提高网络效率。
为了体现WMNs多径路由的优势,文献[11]提出优化的Fortified Ant协议,其创新之处在于将排序算法纳入传统蚁群算法中,同时兼并多径传输协议,且端到端时延性能提升在仿真中确实得到验证。与以上研究有异曲同工之妙的是,李伟等人[12]为了提高WMNs全局收敛速度,在传统蚁群算法中融合细菌觅食算法,仿真实现了WMNs高可靠低时延和规避局部最优的效果。
文献[13]基于传统的队列模型方法,考虑了无线mesh网络的无线特性,分析了网关节点的时延,但是未考虑其链路不确定性和网络演算的理论分析使模拟实验无法反映网络的实际QoS性能。文献[14]基于网络演算理论分析了数据包在无线Mesh网络单路径传输系统中的端到端时延上界以及多路径传输系统中的不同路径间时延抖动上界,然而并未考虑并计算多路径传输系统的端到端时延上界性能。刘宴兵等人[15]提出了一种针对云服务网络的参数建模分析方法,从路径时延组成上明确给出了端到端时延上界和数据积压上界的定量数学解析式,但是并未讨论单节点时延,而且也未与实际仿真值作对比分析。以上文献都未考虑当前节点的处理时延对下一个节点的到达曲线产生影响从而导致时延上界计算不紧致的问题。本文主要研究的是无线Mesh网端到端时延近似上界,是对文献[13-15]等研究的一个拓展。
本文内容结构组织如下:第2节简介网络演算的基本定义、定理;第3节是无线Mesh网端到端时延上界分析计算过程,从单节点到单路径传输系统,再到多路径传输系统层层递进分析,计算和验证端到端时延上界;第4节是对第3节结论的数值分析;第5节是结束语。
2 网络演算基础
2.1 网络演算的基本定义与定理
由Cruz开创并由Chang和Boudec等人完善的网络演算理论是一种新型数学工具,是基于最小加代数理论的一组结论,主要作用是分析网络队列系统性能,它最初是为了保障网络服务质量,解决资源预留等问题,目前主要应用于网络的QoS分析和保障。网络演算的基本定义以及积压界限和时延界限等介绍如下[16]:
定义1(广义增函数):设f是一个函数,如果对于任意的0≤x≤y,都有f(x)≤f(y),则称f为广义增函数。
定义2(最小加卷积):设f和g为广义增函数,f和g的最小加卷积运算为

其中inf表示函数的下确界。
用A(t)和A*(t)分别表示(0,t]时间内数据流相对某一系统的到达过程和离开过程。
定义3(到达曲线):给定一个广义增函数α(t),若对于所有的0≤s≤t,若数据流到达过程A(t),满足A(t)-A(s)≤α(t-s),则称α是A(t)的到达曲线。
定义4(服务曲线):设数据流具有到达过程A(t)和离开过程A*(t),β(t)为广义增函数,若对于所有的0≤t0≤t,存在A*(t)-A(t0)≥β(t-t0),则称系统为数据流提供服务曲线β(t)。
端到端的数据流往往经过了多个网络节点,这些网络节点作为整体提供的服务曲线可由各个网络节点的服务曲线计算得到。
定理1(节点串联):假设一个数据流依次穿过服务曲线分别为β1(t),β2(t),…,βn(t)的n个网络节点,则这n个网络节点串联后提供的总服务曲线为β=β1⊗β2⊗…⊗βn。
定理2(积压界限):假设一个数据流受限于到达曲线α,通过一个提供服务曲线β的系统来传输,则系统的积压上界为到达曲线与服务曲线之间的最大垂直距离,即
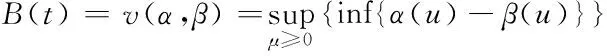
定理3(时延界限):假定一个数据流受限于到达曲线α,通过一个提供服务曲线β的系统来传输,则系统的时延上界为到达曲线与服务曲线之间的最大水平距离,即
d(t)≤h(α,β)

2.2 数据流到达曲线
基于定义3,设ρ是数据流的平均到达速率,σ是数据流的最大突发量,以α(t)=ρt+σ为到达曲线的数据流量称为(ρ,σ)模型。此模型形象描绘了信息流传输过程中的平均行为,模型的到达曲线数学表达式为
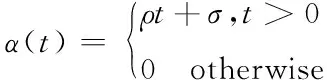
(1)
模型的到达曲线如图1所示。

图1 到达曲线
2.3 数据流服务曲线
基于定义4,采用延迟—速率函数LR(Latency-Rate)来表示服务曲线β(t),表示形式如下
(2)
其中R为服务速率,T是数据流在系统中的服务延迟,可以认为是包处理时延,表示如下
T=L/R+L/C
(3)
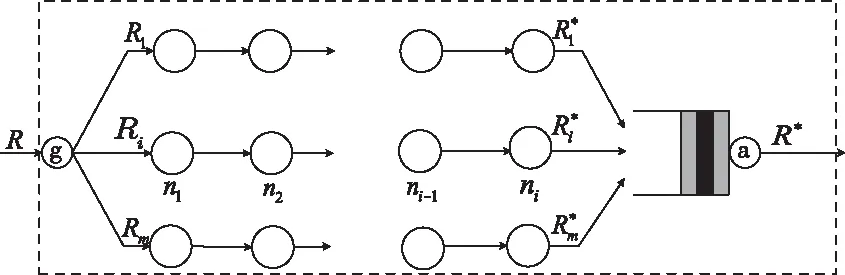
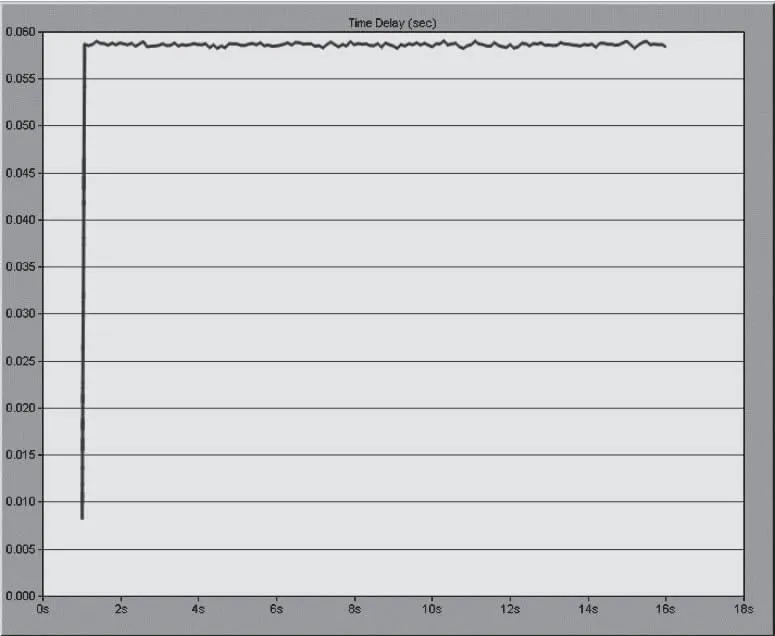
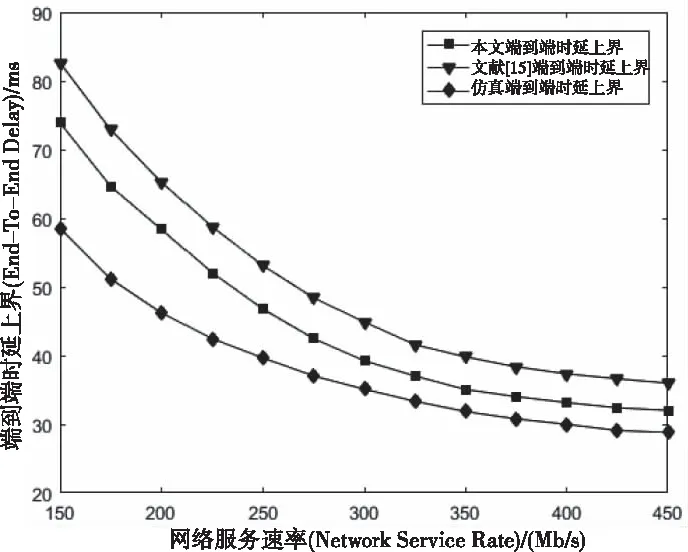
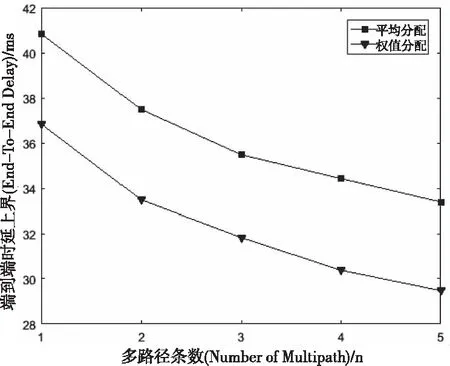
其中L表示(0,t]内的最大包长,C是最大链路速率。这里,平均到达速率ρ≤R 与以往计算方式不同,本文时延上界主要从单节点、单路径和多路径层层递进分析计算,这正是对文献[13-15]的内容扩展,其目的是为了提高时延上界计算的准确度。 当网络数据流A(t)到达一个节点,受到达曲线α的约束,并通过服务曲线β提供服务,单节点的时延由系统缓存的排队时延和处理时延构成,其中处理时延为延迟参数T,而排队时延Dqueue上界看作是最大繁忙间隔[17][18]。 定理4:设数据流到达曲线为α(t)如式(1)所示,服务能力为β(t)的传输服务系统,其单节点的排队延迟上界为 (4) 证明:当t>0时,此时α(t)=ρt+σ Dqueue=inf{t≥0:ρt+σ-Rt≤0} =inf{t≥0:Rt-ρt≥σ} =inf{t≥0:(R-ρ)t≥σ} 所以,单节点i的时延上界为 (5) 无线Mesh网单路径传输如图2所示。假设网络中存在n个节点,第i个节点受到达曲线αi(t)=σi+ρit的约束,服务能力表示为βi=Ri[t-Ti]+,i=1,2,…,n。这里将单路径的端到端时延计算分为两部分:一部分是可变时延,主要是系统缓冲区排队时延;另一部分是固定时延,主要包括节点系统处理时延、转发时延和链路传播时延。而对于固定时延,本文假设n个节点相邻两个节点之间的固定时延依次为d1,d2,…,dn-1。 图2 单路径传输 定理5:设有一条路径包含n个节点,第i个节点数据流的到达曲线为αi(t)=σi+ρit,传输服务系统能力为βi=Ri[t-Ti]+,则节点1到n的单路径端到端延迟为 (6) 证明 用数学归纳法证明: 由上可证明式(6)成立。 2)假设当n=k-1时,式(6)成立,即 3)当n=k时: 图3 多路径传输 多路径传输系统可看作是单路径传输系统的复合模式。假设多路径传输系统中各条路径产生的时延互不影响,此外本文主要考虑的是时延的上界,因而多路径传输时所产生的时延上界为每条路径上时延的最大值加上聚合节点的时延上界。 定理6:假设网络中从节点g到a有m条路径,第i条路径上有ni个节点,各节点的服务能力分别表示为βa=Ra[t-Ta]+,β(i,j)=R(i,j)[t-T(i,j)]+,βg=Rg[t-Tg]+,i=1,2,…,m;j=1,2,…,ni,则从g到a的延迟为 (7) 证:由定理5每条路径上的时延最大值 (8) (9) 其中Ta=L/Ra,ρa=ρ1+ρ2+…+ρm。 综上,结合(8)和(9),得到多路径传输系统端到端时延上界满足 本节分别从单路径传输系统和多路径传输系统两个角度进行端到端时延上界数值仿真验证。在仿真中,针对单路径传输系统,从两方面分析,一是将本文方法与实际仿真时延上界、文献[15]时延上界进行比较来验证结果,二是通过三种不同特征的数据流来刻画本文计算的端到端时延上界在不同条件下的影响。 由上述第二条,三种不同流的长期平均速率和突发量数值分别假设如下:流X为120Mbit/s,200kbits;流Y为200Mbit/s,200kbits;流Z为120Mbit/s,300kbits。其它网络参数采用表1中的设置参数。 表1 网络实验参数设置 用OPNET仿真工具设置一个单路径传输系统,见下图4。实验场景:1000m*1000m,源节点router1的客户端发送速率为120Mbit/s,各路由器router的服务速率初始值设为150Mbit/s,每个节点缓存区大小固定为64个数据包,router1到router7依次相距250m。 仿真过程主要通过发送一系列的测试数据分组来统计端到端时延,首先定义数据包格式64bit,然后在全局场景中设置路由器及客户端,在Node Module中配置如上实验参数,最后设置仿真开始时间为0s,持续时间为20s,时延上界仿真结果在View Results中查看。 图4 单传输系统场景仿真图 图5表示服务速率为150Mbit/s时,在模拟时间内的单路径传输系统端到端时延。 而为了保持以下仿真分析的一致性,下文统一采用流X中的服务参数,根据图5仿真得到的网络端到端时延上界值,与本文计算得到的端到端时延上界、文献[15]端到端时延上界进行比较,结果如图6所示。 图5 R=150Mbit/s时的端到端时延 图6 三者端到端时延上界分析 从图6中可看出,相较于文献[15]端到端时延上界,本文方法计算的时延上界更接近仿真时延上界,这是因为本文考虑了前一个节点的处理时延对后一个节点到达曲线的影响,前后节点的时延相关是时间上的连续关系,与节点的服务规律和到达规律独立并未冲突。另外值得注意的是,当网络服务速率相对较小时,端到端时延上界与仿真时延上界结果偏差较大,这是因为前期较小的网络服务速率会引起节点数据积压造成排队时延增大,并经过网络演算卷积计算后,时延相对偏大。而节点服务能力随着网络服务速率的增大而提升后,两者偏差会越来越小,验证了式(7)是成立的。 另外,在单路径传输系统中考虑X,Y,Z三种数据流,分别从节点个数、服务速率、权值分配三方面,考虑对端到端时延上界的影响。 图7显示单路径传输系统中链路节点数对端到端时延上界的影响,可以看出,时延都是随着链路节点数增加而增大。从式(6)看,当链路节点数增加时,时延主要受平均速率的约束在不断增大,因此网络演算的卷积计算特点更能反映真实的网络性能。 图7 单路径端到端时延和链路节点个数关系 图8显示了端到端时延和网络服务速率之间的关系,不难看出,两者呈负相关,即端到端时延随着网络服务速率增大而减少,这与实际网络情况一致。另外可以看出服务速率小于350Mbit/s时,端到端时延随着网络服务速率增大下降的幅度较大,大于350Mbit/s时,下降幅度趋于平稳。数据流X和Z的端到端时延和网络服务速率之间的曲线几乎重叠,这是因为两种服务有相同的σ,而节点间的输入输出关系正随着网络演算的卷积值而变化,主要受突发量的影响,但影响并不大,但是Z的时延要略大一点。而X和Y的端到端时延和网络服务速率之间的曲线有明显的差别正验证了这点。 图8 端到端时延和网络服务速率的关系 图9显示了端到端时延在固定链路节点个数的情况下与服务速率权值分配之间的关系。假设总服务速率800Mbit/s,数据流X、Y、Z的服务速率分配权值分别为0.2,0.5,0.3。如下图所示,三者端到端时延整体都呈上升趋势,其中X端到端时延最高,Y次之,Z时延最低,这与分析的结果是一致的。因为在相同到达速率情况下,Z分配到的服务速率大于X分配的速率,虽然突发量也会对时延造成影响,但是影响却不大,自然计算出的端到端时延是较小的;而Y与X相比时,到达速率大虽有影响,但对于Y分配到的最高的服务速率,同样影响就不那么明显了。 图9 端到端时延和三种服务权值分配的关系 多路径传输可看作是单路径传输的复合模型,从式(6)和式(7)可看出,不同特征数据流对多路径传输系统端到端时延上界的影响与单路径相同。根据定理6,多路径仿真主要从路径条数、网络服务速率两因素分析对端到端时延上界的影响。 由图3,本文假设源节点g输出的数据分为三条链路到达节点a,链路服务速率分别设置为90Mbit/s,100Mbit/s,110Mbit/s。同时为了对比分析的方便有效,在多路径下本文只讨论分析数据流X在不同情况下的端到端时延上界的相应变化情况。图10表明了在多路径情况下两种流量分配方式随着网络服务速率的增加端到端时延上界的变化情况。即时延上界都随着服务速率的增加而逐渐减小,且减小幅度也在降低,另外还可看出权值分配方式对应时延更低,说明根据不同链路的服务需求分配合适的流量效果更好,降低了部分链路因过负荷导致网络拥塞从而影响全局端到端时延上界。 图10 多路径时延上界和网络服务速率关系 图11表示在链路服务速率350Mb/s,源节点g和节点a服务速率都为500Mb/s仿真条件下,多路径条数和流量分配方式对端到端时延上界的影响,仿真分析数据流X在不同参数条件下的端到端时延上界的结果。很明显两种流量分配方式的端到端时延上界都随着多路径条数增加而增加,权值分配获取到的端到端时延上界比平均分配时延上界低,这同样归功于权值分配方式规避了平均分配方式予链路等量数据而导致部分链路负荷过大,造成网络拥塞,从而影响多路径传输系统端到端时延上界。 图11 多路径时延上界和多路径条数的关系 本文提出的基于网络演算的无线Mesh网端到端时延上界分析方法,利用(ρ,σ)模型作为数据流到达曲线,延迟-速率函数LR作为数据流服务曲线,同时考虑前一个节点的处理时延对后一个节点到达曲线的影响,推导出了单节点时延上界、单路径传输系统端到端时延上界和多路径传输系统端到端时延上界表达式。仿真实验表明,与传统方法相比,本文方法计算得到的时延上界更接近仿真值。为了更准确地分析,在本文计算出的时延上界基础上计算端到端数据积压上界以及时延抖动上界来约束传输系统进行负载均衡是本文下一步的研究方向。3 无线Mesh网端到端时延上界
3.1 单节点时延上界
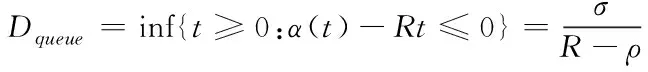

3.2 单路径传输系统端到端时延上界


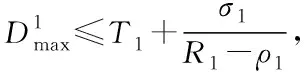
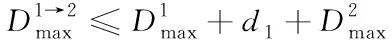
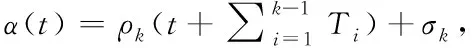


3.3 多路径传输系统端到端时延上界
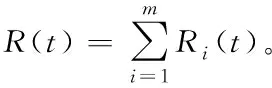

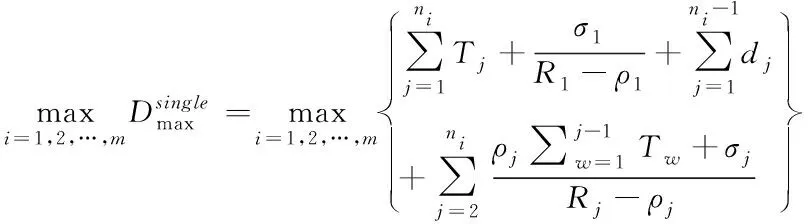

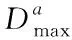

4 仿真

4.1 单路径传输系统端到端时延上界




4.2 多路径传输系统端到端时延上界
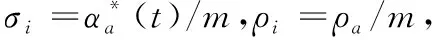

5 结论
