基于CEEMDAN和小波熵的心音信号去噪算法研究
2023-03-29梁春燕袁玉英
刘 倩,徐 彦,梁春燕,袁玉英
(1. 山东理工大学计算机科学与技术学院,山东 淄博 255049;2. 山东省淄博市中医医院心内科,山东 淄博255300)
1 引言
心音是血液在心血管内运动的状态反映,其包含着心脏的生理和病理信息,因此,正确识别心音信号对于心血管系统疾病的诊断具有重要的作用。心音信号是在强噪声背景下采集的生物电信号,噪声对心音信号的正确诊断和识别带来干扰,因而去噪效果将直接影响后续心血管疾病的诊疗。
近年来,小波阈值去噪算法[1-2]和经验模态分解(Empirical Mode Decomposition,EMD)去噪算法[3]已广泛地应用于心音信号的噪声处理。由于小波变换对于信号在时域和频域上都有良好的局部分析特性,选取适当的阈值,能够较好的实现心音信号的去噪处理。但传统阈值的非自适应选取导致在剔除噪声的同时易损失心音信息。经验模态分解算法将心音信号分解成一组由高频到低频排列的模态函数,舍弃前几阶高频噪声的模态分量,并重构剩余的模态分量,最终得到去噪后的心音信号。但简单的舍弃分量、重构分量会导致心音信息的丢失,影响去噪效果。文献[4]提出结合小波变换和EMD的算法优点,利用小波变换滤除掉高频分量中的噪声并保留其中信号成分,从而提高了去噪效果。但EMD在分解过程中存在模态混叠问题,Wu和Huang[5]在EMD的基础上提出集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)算法,EEMD算法[6-8]在信号中混入白噪声,使各阶本征模态函数均值化,以此解决模态混叠问题。而对于信号和噪声分量如何来界定,EMD和EEMD都缺少相关标准,导致最终去噪效果不佳。
结合上述分析,本文提出基于CEEMDAN和小波熵的心音信号去噪方法。算法首先对心音信号CEEMDAN分解;根据噪声能量和信号能量在各阶分量中的区别,利用能量分析界定需去噪的IMF分量范围;采用小波变换将需去噪的IMF分量分解,通过小波熵值自适应地确定每一尺度上的阈值,并完成噪声IMF分量的去噪;最后重构去噪后的IMF分量与信号IMF分量,获得去噪后的心音信号。
2 基本理论和方法
2.1 CEEMDAN算法原理
CEEMDAN 方法是基于 EMD 和EEMD的一种算法,该算法在EEMD基础上,通过对信号添加自适应白噪声来克服模态混叠问题。算法的基本步骤如下:
1)在含噪的心音信号x(n)中添加N个不同的高斯白噪声wi(n),构造新的信号
xi(n)=x(n)+σiwi(n)
(1)
式中σi为噪声的标准差,wi(n)是服从正态分布的白噪声。
2)利用EMD对xi(n)进行分解,得到第一个IMF分量,计算它们的平均值
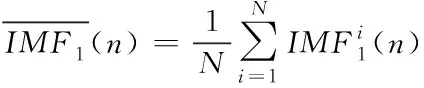
(2)
计算第一个剩余分量

(3)
3)第二个IMF分量如下式(4)计算:
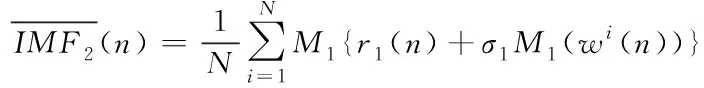
(4)
其中,Mj(·)是信号进行EMD分解操作后的第j个IMF分量。
4)计算第L个剩余分量

(5)
计算第L+1个模态分量

(6)
5)重复执行步骤4),直到剩余分量不再分解为止,即不满足EMD的分解条件,分解结束。
6)原始信号x(n)最终被分解为:
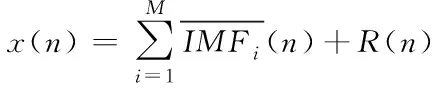
(7)
其中,R(n)为最终的剩余分量。
2.2 小波熵算法原理
小波阈值的选取[9-11]往往决定小波变换的去噪效果,根据小波变换理论可知,信号经小波变换后,信号信息和噪声信息在不同尺度上的分布有较大的区别,而熵衡量信息量的大小,因而通过小波熵值[12-15]自适应地确定每个尺度上的阈值,实现有效滤除噪声的目的。
具体方法:将心音信号经过小波变换后,对尺度j上的高频系数|wj,k|等分为多个子区间,取子区间中熵值最大区间的小波系数绝对值的中值,作为尺度j的噪声估计方差,即

(8)
2.3 小波自适应阈值选取
经前人研究[16-17]及笔者多次仿真,本文采用如式(15)所示阈值[18]计算公式

(9)

3 基于CEEMDAN的心音信号小波熵去噪
基于CEEMDAN算法的心音信号分解,能有效改善模态混叠问题,充分利用噪声和心音信号的能量区别,实现IMFs分量的信噪分离,通过自适应小波熵阈值完成信号去噪,提高了心音信号的信噪比。
3.1 基于能量分析的判别方法
CEEMDAN算法将心音信号分解成从高频到低频的不同模态分量。仿真发现,在低阶分量处,噪声能量很大,随着分解层次增加,噪声能量越来越小,信号能量越来越大。基于信号和噪声的能量在各阶模态分量中表现不同,能量急速上升表明噪声能量减弱而信号能量开始增强;同理,在高阶处能量急速下降表明信号能量从最强开始减弱,因此,在高阶能量急速下降前一阶标记为信噪分界点。
图1是正常心音信号,其信噪比为8dB。图2是带噪心音信号CEEMDAN的分解图。图3是分解后各阶IMF分量的能量图。从图3中分析IMF1的噪声能量最强,IMF2~IMF5噪声能量减小,从IMF5开始,信号能量开始增强,IMF7的信号能量最强,之后能量逐渐降低,所以确定高阶能量急剧下降前一阶,即k=6阶为信号和噪声的分界点。
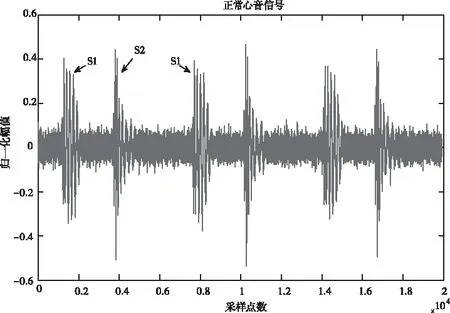
图1 心音信号
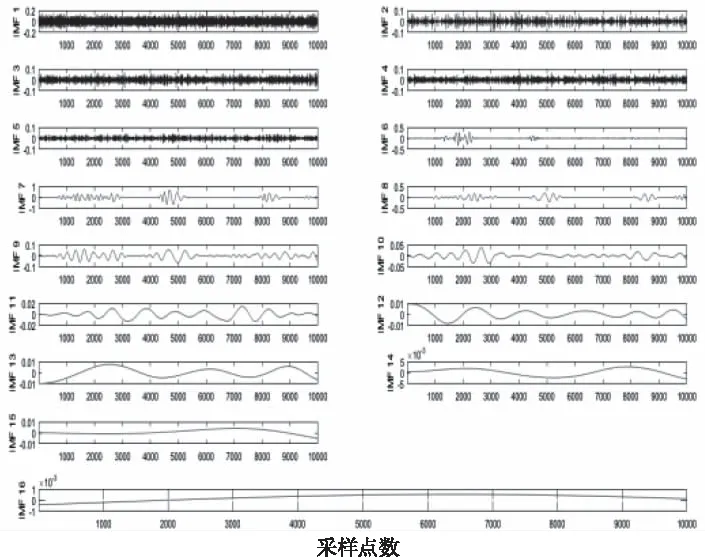
图2 CEEMDAN分解图
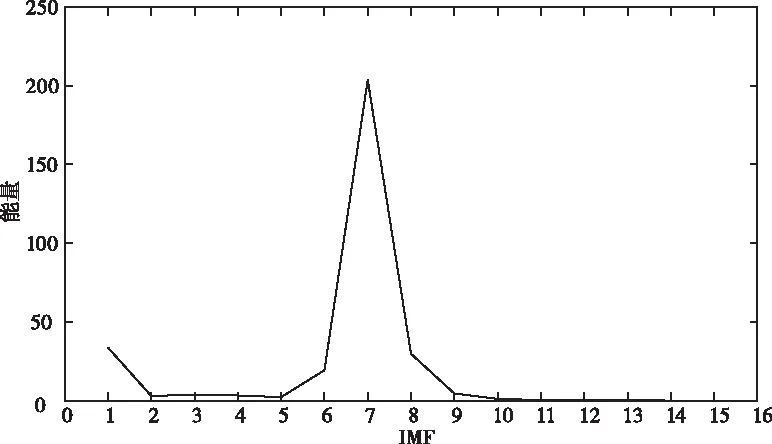
图3 各阶分量能量图
为验证该方法的合理有效性,对8dB的心音信号从IMF2开始叠加IMF分量,分别计算其信噪比SNR和均方根误差RMSE,结果如表1所示。

表1 各阶IMF的SNR和RMSE
其中,SNR的数学表达式如下

(10)
RMSE的数学表达式如下:
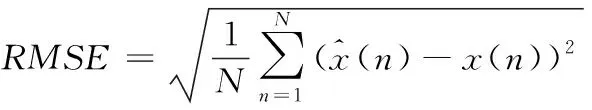
(11)

从表1中可以看出,从IMF2~IMF4合并分量,信噪比逐渐提高,说明噪声成分逐渐减少,心音成分逐渐加强;从IMF5、IMF6开始合并分量,其SNR和RMSE的结果比较接近,达到17dB左右,说明从第五阶开始,信号成分开始增强;而从IMF7合并的信噪比突然降低,说明从第七阶开始合并会丢失部分心音成分,故保留IMF1~IMF6的信号作为待去噪的心音信号分量,进行后续的去噪分析,IMF7之后的分量作为纯净的信号加以保留,与前面分析保持一致。
3.2 基于CEEMDAN的自适应小波熵阈值去噪算法步骤
综上所述,算法步骤设计如下:
Step1:对心音信号进行CEEMDAN分解,获得一系列IMF分量;
Step2:基于IMFs分量的能量分析判定信号和噪声的分界点K;
Step3:将Step2界定的高频分量作为待去噪IMFs;
Step4:选择合适的小波基对需去噪的IMFs分量小波分解,根据式(8)计算尺度j的噪声方差;
Step5:根据式(9)计算尺度j上的自适应阈值,对Step3界定的IMF分量进行小波熵阈值去噪;
Step6:重构经Step5处理后的IMF分量与剩余的IMFs分量,获得去噪后的心音信号。
具体流程如图4所示。

图4 算法流程图
4 仿真结果和分析
本文在MATLAB 2016a仿真环境下,分别采用本文算法与CEEMDAN、EEMD、EMD、小波软阈值4种传统去噪算法分析比较不同信噪比条件下的心音信号的去噪效果。
4.1 正常心音的去噪效果分析
对8dB条件下的正常心音信号分别采用上述5种算法进行去噪处理。算法1采用基于CEEMDAN和小波熵结合的去噪方法;算法2采用CEEMDAN和小波阈值结合的方法;算法3采用EEMD和小波阈值结合的方法;算法4采用EMD和小波阈值结合的方法;算法5采用小波软阈值去噪方法。根据多次仿真结果,本文小波基采用‘db10’,小波分解层次5层,小波熵自适应阈值中参数α取1.25,最终仿真结果如图5所示。
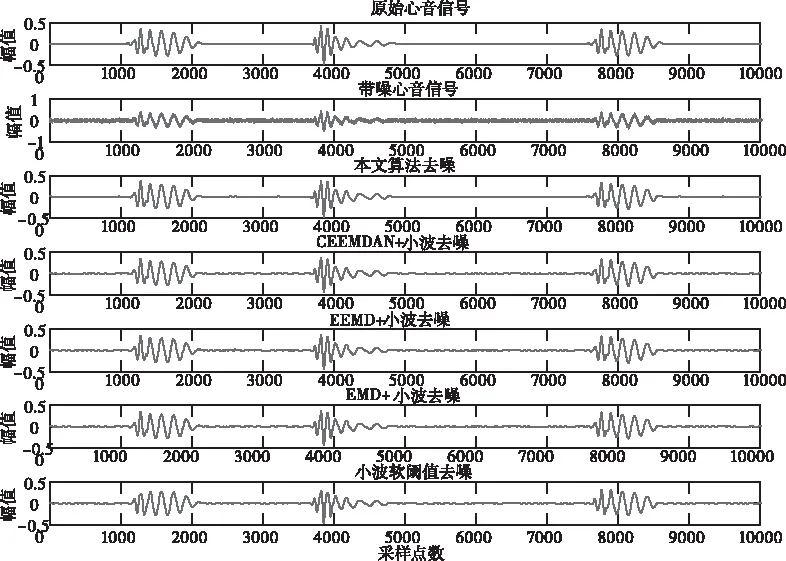
图5 不同算法的去噪效果图(8dB)
从图5中可以看出,5种算法都能很好地保留心音信号的特征,但相较于其它算法,本文算法在S1S2间隙去噪效果更为突出,噪声滤除更加干净。在同一信噪比下,对正常心音信号重复运行多次实验后,分别求取其输出信噪比及均方根误差的平均值。其仿真结果如表2所示,本文相较于直接去掉前几阶分量的方法,信噪比提高了4dB左右,比直接小波阈值去噪,信噪比提高了3dB左右,对于其它经验模态分解方法,信噪比有了不同程度的提高,同时RMSE明显减小。

表2 不同算法的SNR和RMSE
4.2 含S4心音的去噪效果分析
S4信号特别微弱,信号特征相较于S1和S2不明显,但对于心血管疾病的临床判断具有重要的作用。同样,采用上述5种算法对3dB噪声条件下含S4的心音信号进行去噪分析。图6是去噪效果图。

图6 不同算法的去噪效果图(3dB)
从图6中可以看出,经EEMD、EMD和小波软阈值这3种算法去噪之后,S1的波形特征有些失真,说明部分心音信息丢失。由于S4在9000-10000采样点处幅值很小,加入噪声之后,S4已基本被噪声淹没,因此,去噪算法的关键在于滤除掉间隙期(S4S1、S1S2和S2S4间)的噪声且能保留S4的特征。对于本文算法在间隙期噪声基本滤除掉,而其它算法间隙期的噪声去除的不够干净,导致9000-10000处的S4信号特征不明显,为后续心音信号的识别及心血管疾病的判断造成影响。
4.3 不同噪声特性对算法性能的影响

图7 信噪比曲线(正常心音信号)
为验证不同去噪算法的效果,本文采用正常心音信号和含S4的心音信号作为实验对象,在不同噪声环境下多次运算求取信噪比和均方根误差的平均值,输出结果如图7-图10所示,在相同的噪声环境下,小波软阈值的去噪效果最差,EEMD和EMD算法去噪效果在低信噪比下比较接近,随着信噪比的增加,EEMD去噪效果更为明显,相较于与小波阈值结合的CEEMDAN算法,与小波熵结合的本文算法信噪比提高更加显著,更能保留心音信号的特征。

图8 RMSE曲线(正常心音信号)
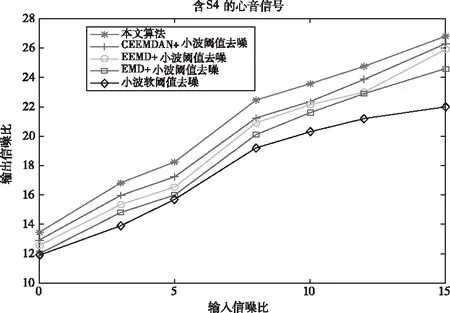
图9 信噪比曲线(含S4心音信号)

图10 RMSE曲线(含S4心音信号)
5 结论
1)本文通过CEEMDAN算法对心音信号分解为多个模态分量,针对噪声能量和信号能量在模态分量中的区别,判定信噪分界的拐点;根据小波分解后每一尺度上的信号和噪声的熵值差别,利用小波熵确定每一尺度上的噪声方差,通过阈值算法确定阈值,进行去噪处理。
2)实验部分,分别比较本文算法与其它4种传统去噪算法在不同心音和不同信噪比条件下的去噪效果。通过分析,本文算法去噪后的信噪比较高,均方根误差较小,具有良好的噪声抑制能力,能较好地保留心音信号的特征。
本文算法实现了噪声的有效滤除,为后续心音的识别和心血管的判断提供良好的数据基础,也为今后信号去噪方法提供了一种思路。
