改进零视差像素点重组的图像数字水印算法

李播阳，张 频，吴 江

(1. 江西科技学院，江西 南昌 330003；2. 南昌大学建筑与设计学院，江西 南昌 330031)

1 引言

在计算机技术与互联网技术的推动下，社会正朝着信息化的方向发展，促进信息传播载体从纸质版到电子版转变，逐渐打破数字信息传输所受到的时间、空间等外界条件限制，令数字信息的交换与传输随时随地都能够轻易实现。由此产生的负面问题便是复制、无限制传播、修改、非法占用未经授权或许可的数字化信息产品等大肆违规操作[1]。随着国民对隐私安全意识的提升，信息安全保护的关注程度越来越高。为保护数字化的产品内容，使作者的合法权益得到应有的保障，有效防止版权纠纷的数字水印技术[2]应运而生，并在主流的图像载体上得以广泛应用。

数字水印技术作为信息隐藏技术[3]的重要应用，引起了众多相关人员的研究热情，取得了成效显著的研究成果。例如：岳桢[4]等人基于直方图，提出面向2Bin多进制图像的数字水印算法；孙晓霞[5]等人通过融合离散小波变换与奇异值分解，设计出基于机器学习的数字水印算法。前者能较好地抵抗几何攻击与信号处理攻击，后者则具备较强的鲁棒性。基于目前的研究成果与优势，以三维图像[6]为目标，研究出一种数字水印算法，拓宽三维图像的应用前景与规范传播范围。该方法的研究重点如下：

1)利用多个二维的三角面片来描述三维图像，有助于降低数字水印算法的构建难度；

2)采用亮度-色度模型转换图像色彩，可加强视觉感知的敏感度，保证初始图像质量；

3)通过轮廓波分解，解得最后一层的各方向图像能量，使隐秘性与鲁棒性同时得到保证。

2 三维图像的色彩转换

将三维图像看成是由多个二维三角面片[7]构成的数据，建立三维空间的平面点-线模型，用于描述复杂的三维图像，降低数字水印算法的构建难度。假设三维图像I(x，y，z)中像素点o的三维空间坐标是(x，y，z)，则该像素点的索引值so计算公式如下所示

so=f(x，y，z)

(1)

其中，f(·)表示函数运算。

组成三维图像I(x，y，z)的l个三角面片均由三个像素点的索引值组成，则该三维图像的点-线模型界定式如下所示

I(x，y，z)=(T1，T2，…，Tl)=((s1，s2，s3)，…，(sa，sb，sc))

(2)

其中，Ti表示不同的三角面片；(sa，sb，sc)表示构成三角面片的三个像素点索引值。

该模型描述的三维图像无法展现出较好的视觉效果，故利用亮度-色度模型[8]转换图像色彩，将数字水印嵌入色度值内，加强视觉感知的敏感度，保证初始图像质量。色彩转换实现形式如下所示

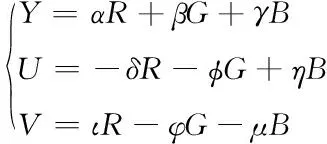
(3)

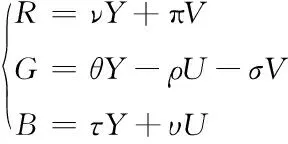
(4)

其中，Y、U、V分别表示亮度-色度模型的亮度、蓝色分量与红色分量；R、G、B分别表示红色-绿色-蓝色模型[9]的三个色彩分量；各分量前的代数项分别表示两个色彩模型在转换过程中对应分量之间的相关性系数。

3 零视差点重组

基于经过色彩转换的三维图像，设定双目视距为u，眼睛与三维图像的间距是S，图像深度为L，若图像内外界线的最大视差值各是e1、e2，则图像深度的极值Lmin、Lmax计算公式如下所示

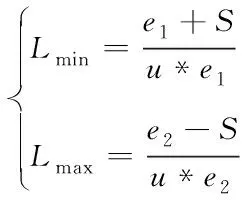
(5)

利用灰度等级量化图像深度极值，得到下列三维图像内外界线的景深值Ln、Lw

(6)

其中，P表示经过灰度等级量化[10]的成像景深。

结合相似三角形原理[11]，通过下式解得图像各像素点的视差dis

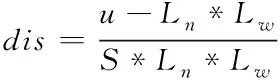
(7)

根据解得的视差值，以零视差为基准，利用归一化协方差的灰度匹配方法，调整各像素点坐标，完成像素点重组。具体实现流程如下所述

1)将任意两个零视差像素点C1(i，j)、C2(i，j)依次作为三维图像中心，选取两像素点的对应窗口c1、c2；

2)利用下列计算公式求解出零视差像素点C1(i，j)对应窗口c1的归一化协方差

(8)

由此推断出在各自窗口c1、c2内，两个零视差像素点C1(i，j)、C2(i，j)对应灰度方差F1、F2的计算公式，分别如下所示

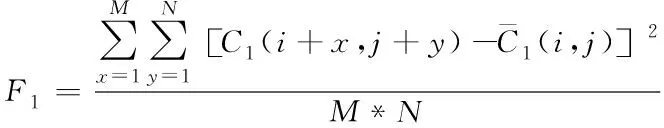
(9)

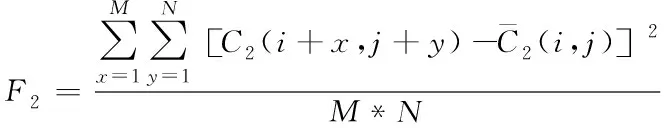
(10)

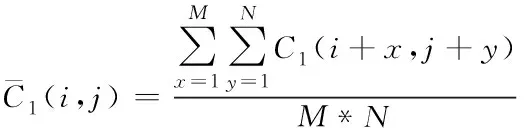
(11)

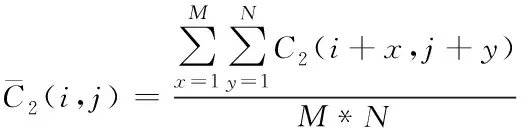
(12)

以此类推，得到所有零视差像素点对应窗口的归一化协方差；

3)根据各窗口的归一化协方差，采用下列公式调整各像素点坐标，得到重组图像A(x，y)

(13)

其中，g指代零视差的像素点序数。

4 三维图像数字水印算法

将零视差的重组图像作为待嵌入水印的载体图像，结合轮廓波变换方法[12]，构建出三维图像的数字水印算法，完成数字水印的嵌入。假设重组图像A(x，y)(即载体图像)的规格是M*N，数字水印的二值图像B(x′，y′)规格是m*n，则三维图像数字水印算法的实现流程如下所述：

1)轮廓波分解[13]重组图像A(x，y)，得到多个包含四个分解方向的分解层，设定所得的多个分解层及对应分解方向是数字水印的嵌入密钥[14]；

2)利用下列表达式，针对最后分解层，求解出各分解方向的图像能量，确保重组图像同时具备较好的隐秘性与鲁棒性

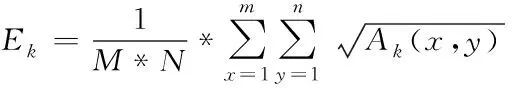
(14)

其中，k表示任意分解方向，k=1，2，3，4；Ak(x，y)指代k方向上的像素值。

4)选取各像素块中两个固定方位的系数λ1、λ2，求取两系数之间的差值ε，结合预设的水印嵌入强度[16]κ，推导出下列轮廓波交换系数的交换判定条件方程组

(15)

5)利用轮廓波逆变换策略，处理得到的各分解方向图像，通过拼接、融合，取得带有数字水印的三维图像。

5 实验研究

5.1 实验对象与评估指标选取

针对直径600mm、高200mm的三维图像(见图1)展开仿真，选取条件相对熵xds、峰值信噪比psn及相似度nc三个指标，从相对客观的角度，评估所提算法所嵌入数字水印的安全度、隐秘度及嵌入质量，指标数值与评估结果之间呈正相关性。一般来讲，若峰值信噪比大于50dB，则图像质量良好，噪声较少，水印隐秘度较好，若不小于60dB，即表明图像质量较优，几乎不存在噪声，水印隐秘度绝佳；对于条件相对熵与相似度两指标，数值越趋近于1，则水印的安全度与嵌入质量越理想。为检验所提算法的优越性，将直方图数字水印算法与机器学习数字水印算法作为对比方法进行比较分析。

图1 初始的三维图像示意图

三种评价指标的计算公式分别如下所示：

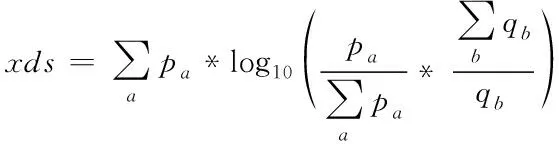
(16)

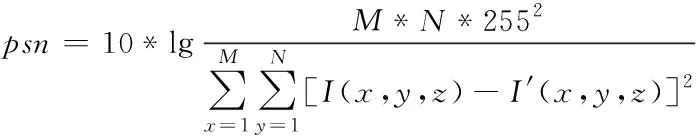
(17)

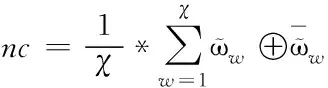
(18)

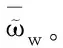
5.2 三维图像数字水印效果的感官分析

三种算法就目标图像(见图1)嵌入的数字水印均为25×25尺寸的二值图像，如图2所示。

图2 不同算法的数字水印图像

从视觉角度对比各算法的数字水印发现：三种算法的数字水印都无法用肉眼观察到，相比直方图数字水印算法与机器学习数字水印算法，所提算法的隐蔽性较好，能够满足数字水印的安全性、不可感知性等要求。这是因为所提算法根据像素点的零视差值与窗口的归一化协方差，通过调整各像素点坐标，完成像素点重组，故有效抑制了图像噪声形成。

5.3 三维图像数字水印算法性能的客观评价

对于不同算法的微观差别，视觉判断不具备良好的说服力与可靠性，故采用条件相对熵、峰值信噪比及相似度等指标，进一步验证所提算法的优越性与实践性。利用simulation仿真软件，模拟图2中三种算法对应数字水印图像的各项指标值，比对情况如图3所示。

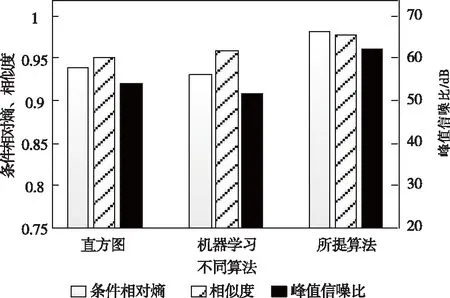
图3 不同算法的数字水印评估示意图

根据图3中三种算法的图像评估结果可以看出，所提算法图像的峰值信噪比超过60dB，条件相对熵与相似度大于0.95，各项指标均高于两个对比方法。这表明该算法通过融合零视差点重组策略与轮廓波变换策略，不仅提高了数字水印的嵌入效果与图像质量，而且加强了水印的隐秘度、安全度。

为检验数字水印对各类攻击的防御能力，利用测评水印的Stir Mark攻击软件，在所提算法的数字水印图像中添加多种攻击方法，不同的攻击手段与攻击形式如表1所示。

表1 攻击手段与方式

针对表1中的攻击形式，测试所提算法的应用效果，结果如图4所示。

图4 不同攻击下的数字水印评估示意图

根据图4中受到各类攻击时所提算法的图像评估结果可以看出，无论攻击手段如何变换，该算法的数字水印图像峰值信噪比始终保持在50dB以上，条件相对熵与相似度两指标也一直居于0.93以上，即便是较高的数字水印要求也能满足。这说明所提算法具备较强的攻击抵御能力，在多种形式的攻击下，依旧能凭借轮廓波分解、变换过程中设立的多重嵌入密钥，令数字水印保持高水平的嵌入质量与隐秘度、安全度。

6 结论

在图像技术日益发达的今天，三维图像作为一种新兴的数字信息应用广泛，但相关的数字水印技术研究却正处于起步阶段，故面向三维图像，提出基于零视差点重组的数字水印算法，以期为此类产品的版权保护，提供一些技术上的支持。在实用性方面，集人眼视觉模型、网络安全等学科知识于一体的数字水印技术仍存在诸多亟待解决的问题，为使所提算法能真正服务于数字信息时代，得到长足发展，应就几个重点作进一步探索，比如：数字水印容量、其它攻击手段、零水印等。