高速履带车辆轮履脱离机理分析与仿真研究

蔡文斌，刘 洋，赵韬硕，陈 兵

(1. 中国北方车辆研究所，北京 100072；2. 北京科技大学机械工程学院，北京 100083)

1 引言

高速履带车辆区别与轮式车辆的最显著特点之一，是利用履带行驶系统来完成自铺路面的行走，使得履带车辆的野外行驶能力，越障能力和机动性能都得到了保证。随着现代履带车辆对机动性要求不断提高，车辆在斜坡行驶、软地急转弯等恶劣工况行驶过程中履带脱轮现象时有发生，履带发生脱轮不但使车辆丧失机动性，陷入“瘫痪”状态，而且直接影响了车辆的行驶通过性和作战任务等。因此有必要围绕履带车辆的履带脱轮问题进行相关研究，分析履带刚度特性、诱导齿及负重轮设计参数对履带脱轮影响的灵敏性，并优化相关设计变量来提高履带系统的运行稳定性。

近年来，国内很多学者对高速履带车的研究工作主要集中在高速车辆悬挂系统动力学特性和履带行动装置的研究上，并得到了一定的研究成果。例如：云忠等人基于多体动力学理论建立了履带车悬挂系统半车振动力学模型和动力学方程，并用RecurDyn仿真验证了高速履带车翻越垂直壁障时悬挂系统参数对其乘坐舒适性和稳定性的影响[1]。卞美慧等人提出了两种负重轮载荷分配的方案，并对两种负重轮载荷分配方案下车辆的平顺性进行了仿真分析[2]。马星国等人以某履带车辆悬挂系统为例，利用动力学软件RecurDyn建立单轮动力学模型，并基于车辆动力学与冲击碰撞原理，研究油气弹簧与液压缓冲器对悬挂系统性能影响及车体行驶过程中悬挂系统缓冲、吸振性能[3]，刘冰铁等人基于ANSYS Workbench 平台，在三种典型工况下，对三种轮盘结构形式的负重轮的应力分布情况进行了计算，得到了在相应工况下应力的最大值[4]。上述研究并非针对履带脱轮问题展开的研究的工作，但对本文具有一定的指导作用。

查阅国内外近20年高速履带车辆履带脱轮机理研究的公开文献，受技术保密或问题过于复杂等因素影响，很难发现与高速履带车辆脱轮机理研究紧密相关的文献，仅发现少数学者围绕脱轮现象开展了部分研究工作。例如：钱尧一等为解决三角履带脱轮问题，使用多体动力学软件RecurDyn建立了三角履带车辆的模型，研究了其诱导轮张紧装置的预紧力参数变化对履带张紧力和前端垂向位移的影响规律[5]；朱艳芳等运用ADAMS软件建立了履带车辆行走系统虚拟样机模型，并对其高速行驶工况的“脱轮”问题进行仿真分析[6]；张燕等使用RecurDyn软件对履带及负重轮的位移变化进行研究，分析了履带脱轮的原因[7]；张涛考虑了履带车辆主要结特征构，建立了针对其高速行驶中脱轮问题的行走系统动力学模型[8]；韩寿松通过RecurDyn和AMESim软件构建了履带车辆整车动力学、路面和油气悬架液压系统模型，分析了油气悬架履带车辆蓄压初始充气压力等参数对履带车辆脱轮故障的影响规律[9]。

本文在上述研究的基础上将履带考虑成柔性体，对履带的刚度值进行了有限元仿真分析。并以ADAMS软件为仿真平台建立了可测试履带从负重轮脱出难易程度的虚拟样机，利用正交试验的方法开展了对履带扭转刚度、拉伸刚度、侧向刚度和诱导齿及负重轮设计变量对履带脱轮影响的仿真研究；最后使用神经网络对仿真结果进行拟合，并对拟合表达式进行GA算法寻优，得到了防止履带脱轮主要影响因素的参数最优值，以提高履带的运行稳定性。

2 高速履带车辆“履-轮脱离”机理分析

从履带车辆易脱轮的现象出发，具体考虑高速履带车辆行驶工况，可得知履带脱轮的本质是行走系统中转动的各轮与履带的相互位置发生倾斜后，继续行走履带将会从行走系统轮上脱下的现象。当履带的纵向轴线与负重轮的滚动平面不平行时，滚动的负重轮与履带诱导齿发生接触继而导致履带脱轮。假设负重轮与诱导齿接触于一点a，如图1所示。

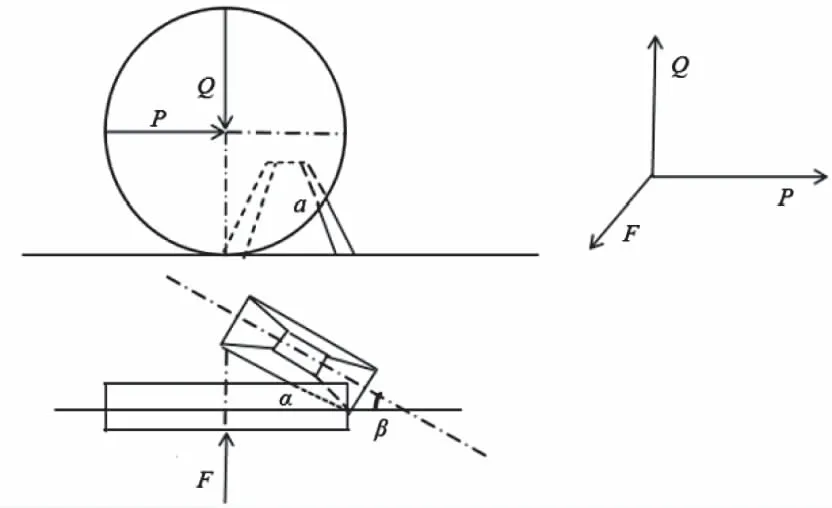
图1 负重轮与诱导齿的接触

选取坐标轴的方向使作用在负重轮上的三个相互垂直的力Q，P，及F的方向平行。Q，P分别表示平衡肘作用于负重轮上的力，F表示车辆在不同工况下负重轮所受的横向力。根据文献[10]可知，将坐标轴的原点设在接触点a，则QP平面与负重轮的滚动平面平行。过a点引一与诱导齿断面相切的平面(平面t)。此平面的位置决定于平面t及PF交线的角度β，及通过点a的法线的角度α。其在a点的受力关系如下图2所示。

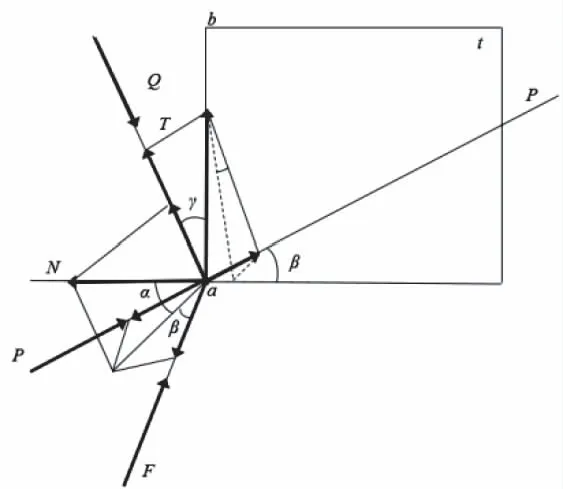
图2 在接触点作用于负重轮上的力

图3 α、β、及γ之间的关系

在负重轮的a点上，作用有以下各力：Q，F，及P。因为负重轮在滚动，而平面t是固定的，所以在a点发生滑动摩擦。摩擦力Fr应该同时在两个平面内：即在负重轮的滚动平面QP及在与诱导齿断面相切的平面t内。此时，摩擦力Fr在两平面的交线ab上，以γ表示直线ab与轴线Q的倾角，则摩擦力可以表示为

Fr=μN

(1)

式中，μ为滑动系数；N为导向齿对负重轮的法向反作用力。Fr和N力的和形成导向齿作用于负重轮上的a点的反作用力。因此在负重轮上有与Fr和N相平衡的力F、Q及P的作用。由图2可写出点a的平衡条件如下

P=Ncosαsinβ-Tsinγ

(2)

Q=Nsinα+Tcosγ=N(sinα+μcosγ)

(3)

F=Ncosαcosβ

(4)

联立方程(2)、(3)、(4)可得

(5)

以α及β角来表示γ角，三者关系如下图3所示，则可写出

h=acosγ

(6)

h=bcotα

(7)

b=csinβ

(8)

a2=c2+h2

(9)

在此基础上，可以推得

(10)

将其带入式(5)中，得到

(11)

由上式，可推得履带不脱轮的条件为

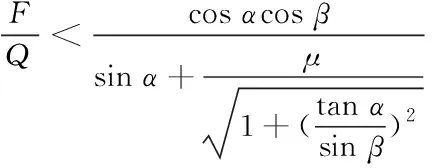
(12)

由式(12)可知，摩擦系数μ越大，则履带发生脱轮所需要的横向力越小，即履带发生脱轮的概率越大。因此，如果金属诱导齿与负重轮的橡胶轮缘接触时，其发生履带脱轮的机会比两个摩擦表面均为金属的机会要大。这为研究防止履带脱轮措施提供了一定的理论依。α及β角对履带脱轮也具有一定的影响：α角愈大，即切面t的倾斜越大，履带发生脱轮的概率也越大。β为负重轮与诱导齿的相遇角，该角度越大，履带发生脱轮的概率也越大。

3 履带刚度特性的有限元仿真分析

履带销上硫化有橡胶衬套，故相邻两块履带板间的相互作用为柔性连接，可将这种柔性连接等效为弹簧阻尼系统。该柔性连接模型使履带具有一定的刚度特性而非纯刚体结构。当履带受到不同的工况载荷时，就会发生相应的变形，其变形过程及柔性连接模型如图4～6所示。履带的刚度特性对履带脱轮产生重要影响，为了分析履带刚度对履带脱轮的灵敏性，需要将一段履带模型分别在有限元软件中建立拉伸，横推，扭转三种工况，得到相应的仿真曲线，最后拟合出履带在此三个方向的刚度值。

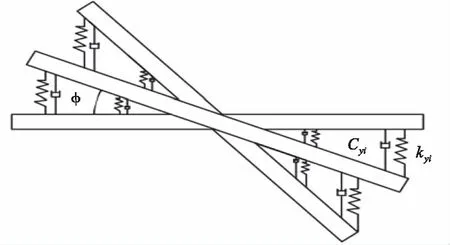
图4 履带扭转工况载荷下的模型

图5 履带横推转工况载荷下的模型

图6 履带拉伸工况载荷下的模型

3.1 履带有限元模型的建立

为了在ABAQUS中来模拟计算履带三个方向刚度值，需要在履带销上硫化有多个天然橡胶衬套，采用tie连接来模拟履带板和橡胶衬套之间的过盈连接。为节省计算机时，对模型进行如下处理：履带板端连器及诱导齿变形较小，网格划分可以较粗大，而对履带销及橡胶衬套处网格进行细化，忽略几个不重要的圆角倒角特征[11]。履带模型如图7所示，橡胶模型采用二阶Odgen模型，近似不可压缩模型，主要参数如表1所示。

图7 履带及橡胶部分模型

表1 橡胶模型主要参数

3.2 仿真分析过程及结果汇总

履带的结构特征复杂，由于其结构特点选取六面体单元进行离散化，将履带离散为一系列单元，各单元在节点处相连，相邻单元之间通过公共节点传递力[12]。考虑履带在实际工程中受力变形情况，需要设置合理的边界条件和工况。本文共分为三种工况载荷，拉伸工况载荷、横推工况载荷、扭转工况载荷。在分析履带受到纵向拉伸工况载荷时，将履带的一段的固定，另一端施加一定的位移，单个履带板的有效长度取履带板中两个履带销中心距离为107 mm，履带模型的有效长度为314 mm。在分析履带板扭转工况时，建立多块履带板模型，且一端固定，一端施加一定扭转角度，履带的有效长度为628mm；当履带板受到横向推力时，边界条件为履带板两端固定，处于中间位置的端连器受到横推位移，履带的有效长度为628mm。其得到的履带应力云图及刚度曲线如图8所示。

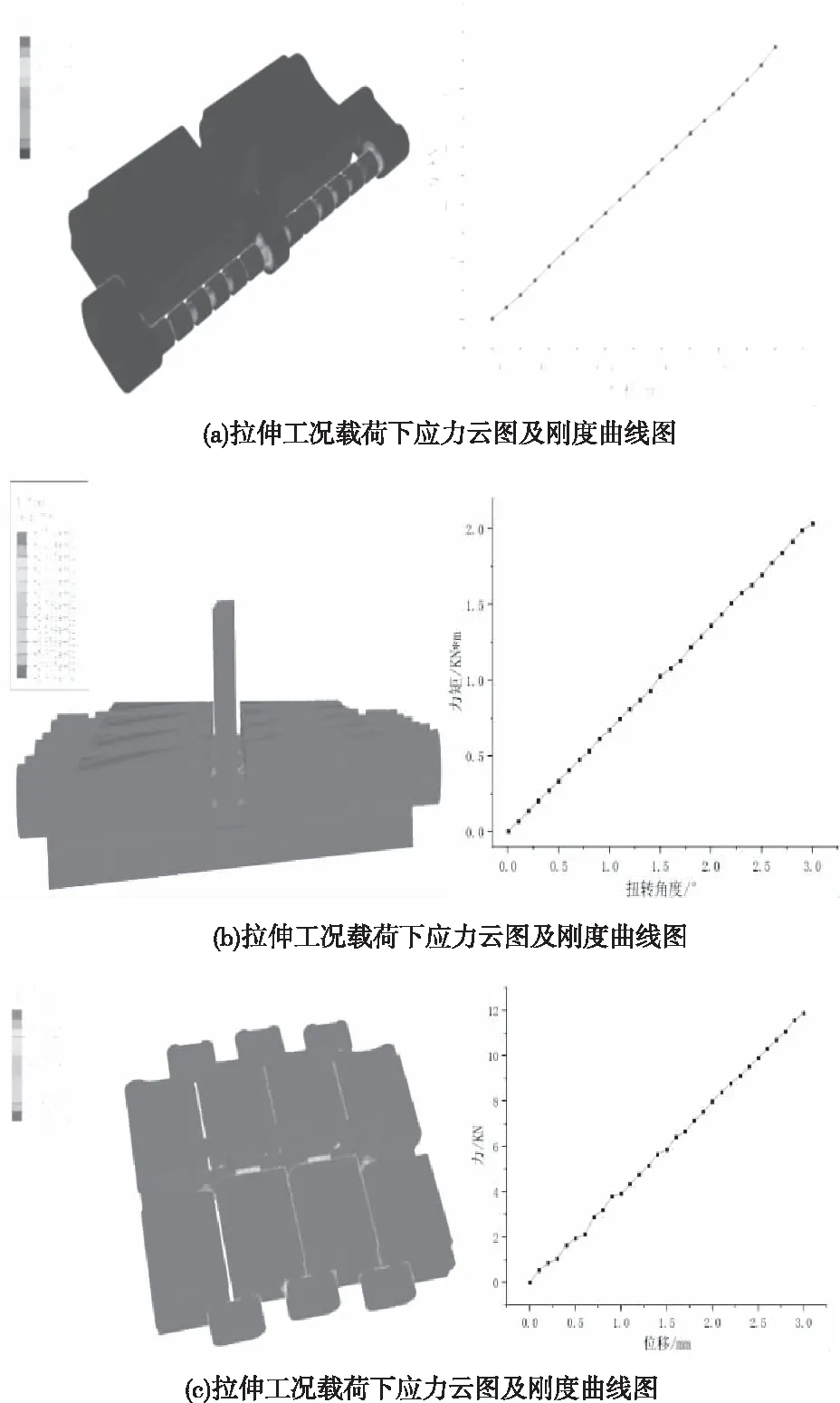
图8 三种工况载荷下履带应力云图及刚度曲线图

将计算结果进行汇总，如表2所示。

表2 三种工况载荷下履带刚度模拟仿真结果

4 试验设计与仿真分析

4.1 试验设计方法

为测试不同刚度特性履带及诱导齿、负重轮设计参数从双胎负重片间隙中脱出的难易程度，建立了如图9所示履带脱轮的多体动力学模型。

图9 模拟履带脱轮多体动力学模型

该模型在试验过程中可以为履带施加扭转力矩、侧向力，驱动履带产生扭转、侧向变形。当负重轮向前移动时，在不同的履带刚度及诱导齿、负重轮设计参数下，履带在受到载荷发生变形之后，履带脱轮的机会不等。为探究履带刚度、弹簧刚度、诱导齿及负重轮设计参数对履带从负重片间隙中脱出概率的影响，用三维软件SOLIDWORKS组装好不同参数履带模型，导出成STEP格式文件，在多体动力学软件ADAMS中进行仿真分析[13]。在ADAMS中，用衬套力代替相邻履带板间的柔性连接模型。例如：当给履带施加扭转工况载荷时，将履带一段固定，利用阶跃函数STEP(TIME，0，0，t，n)，给履带另一端施加一定扭矩，使得履带发生相应的变形，t为时间，n为载荷值。

采用正交试验方案设计，以履带三个方向刚度、诱导齿齿形角度、负重轮轮缘角度为影响因素，负重轮在履带上移动的距离为试验指标，进行仿真分析。试验共分为两大组工况：履带受到恒扭矩工况和履带受到横推力工况。正交试验设计如表3所示。在同样的载荷试验条件下，不同参数的设置，导致履带脱轮发生的概率不尽相同，通过与用户的交流后，本文统一定义为：负重轮向前移动的距离越大，则轮履脱带概率越小。图10，图11为负重轮及诱导齿相关设计参数位置示意图。

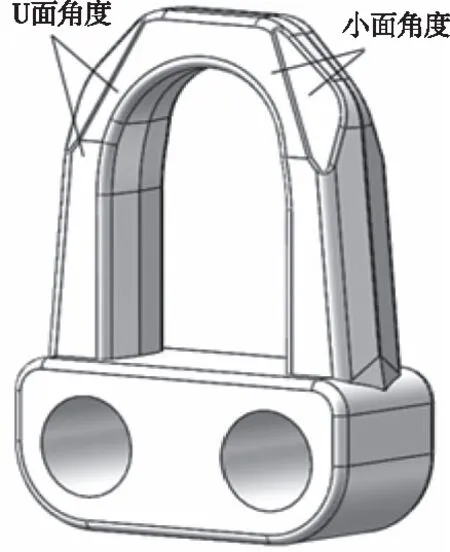
图10 负重轮因素参数变化部位

图11 诱导齿因素参数变化部位

表3 履带脱轮影响因素分析表

4.2 试验结果分析

在仿真过程中，当负重轮即将脱出时，记录下负重轮移动的距离(mm)，结果如表4，表5所示。表4为履带受扭转工况，表5为履带受横推工况，图12表示在两大组工况下不同因素对负重轮行驶距离变化的影响趋势。其中A1表示履带纵向刚度(kN·m·mm-1)、A2表示履带横向刚度(kN·m·mm-1)、A3表示履带的扭转刚度(kN·m2/°)、A4表示负重轮轮缘角度(°)、A5表示弹簧刚度(kN·m-1)、A6表示诱导齿高度(mm)、A7表示诱导齿U面角度(°)、A8表示诱导齿小面角度(°)，Ki表示某一个水平下，对应因素的试验结果之和，ki表示在相应水平下，对应因素试验结果的平均值，R表示极差。

表4 扭转工况履带脱轮正交试验表

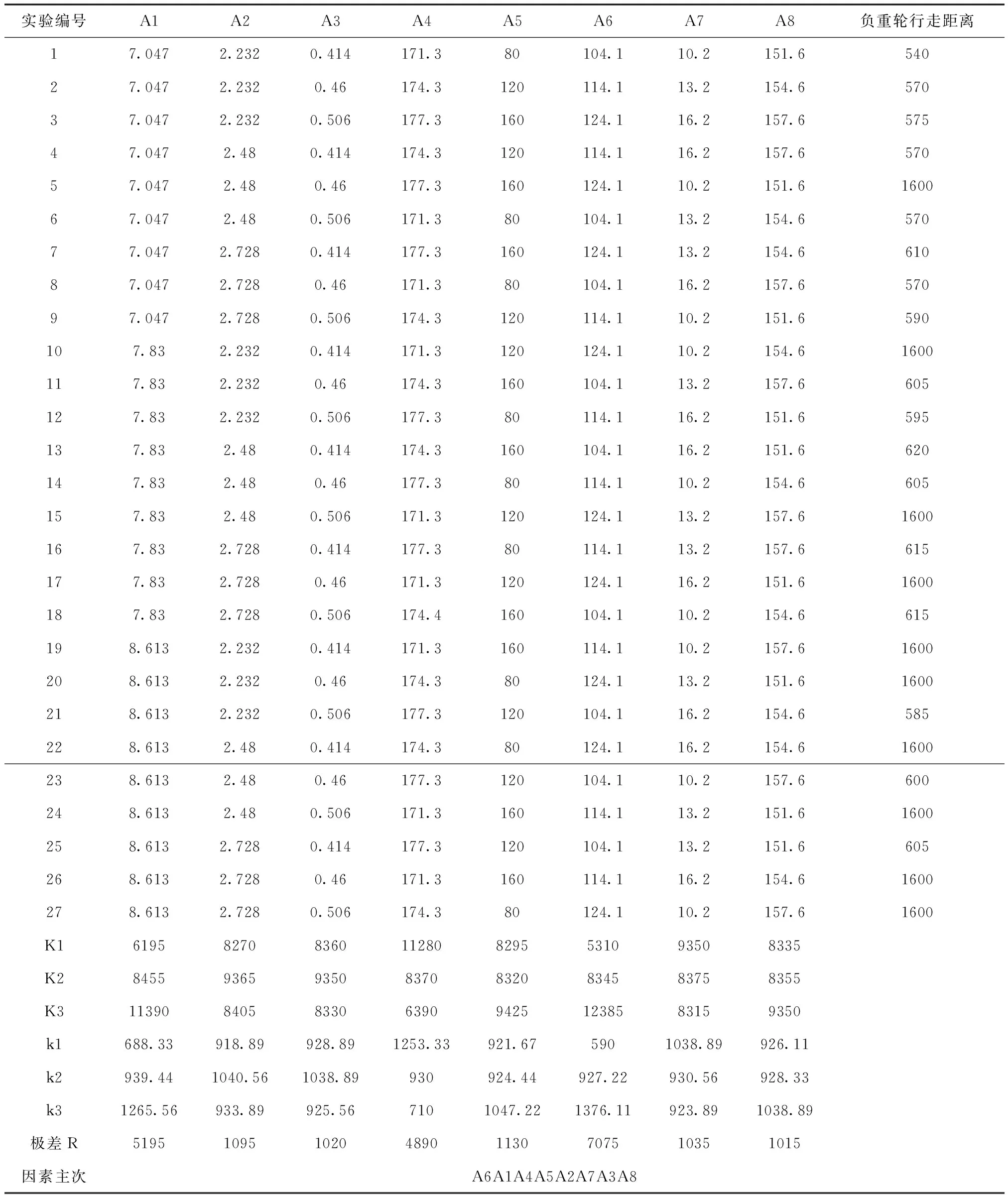
表5 横推工况履带脱轮正交试验表

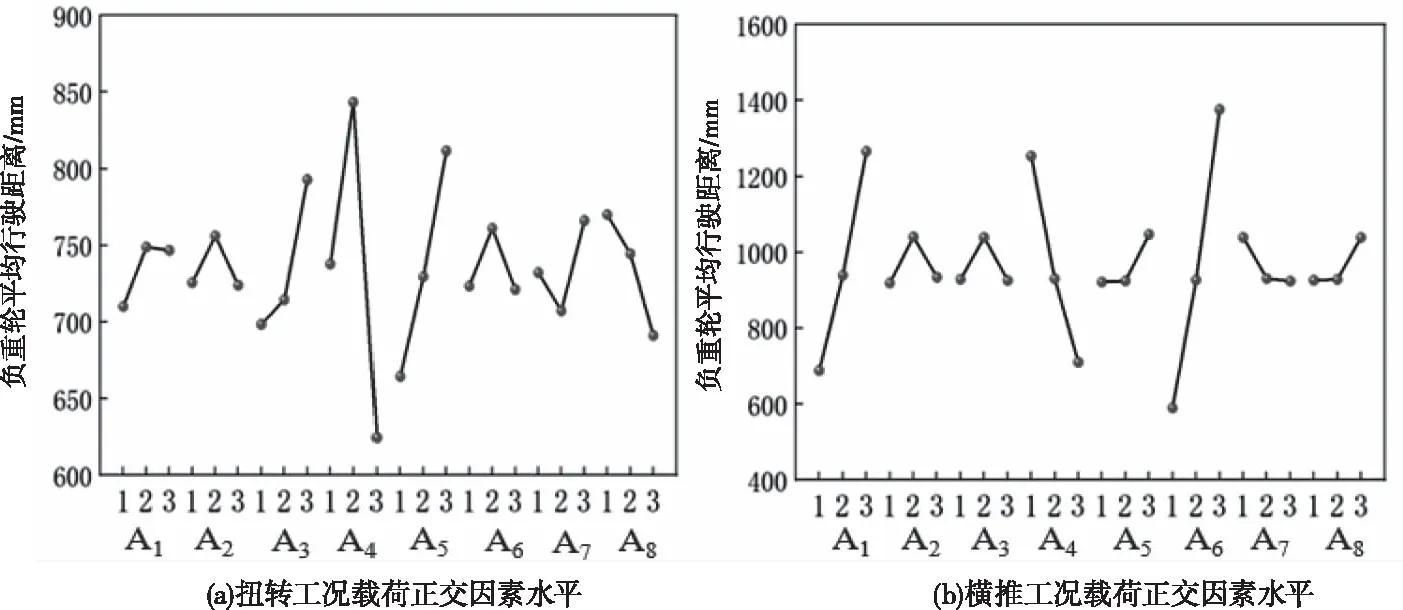
图12 两种工况下各因素对负重轮行驶距离影响的趋势图

从图12中可以看出不同的刚度参数，诱导齿齿形及负重轮设计参数，对履带的运行稳定性影响的趋势有很大不同。从表4中可以看出在扭转工况中设计参数对履带运行稳定性影响程度的排序为：A4>A5>A3>A8>A7>A6>A1>A2。其中A4、A5、A3对履带脱轮影响较大，A4为负重轮轮缘角度，A5弹簧刚度，A3为履带扭转刚度。当履带受到扭转工况载荷时，履带沿纵向发生扭转变形，诱导齿偏移角度较大，当负重轮运动到该处时，负重轮会以很快的速度骑上邻近的诱导齿，或者以轮缘紧贴诱导齿U面而发生负重轮脱带，所以在扭转工况时，履带轮缘角度，负重轮安装架的弹簧刚度及履带的扭转刚度参数影响较大。

从表5中可以看出在横推工况中设计参数对履带运行稳定性影响程度的排序为：A6>A1>A4>A5>A2>A7>A3>A8。其中A6、A1、A4对履带脱轮影响最大，A6为诱导齿高度，A1为履带纵向刚度，A4为负重轮轮缘角度。当履带受到横向力时，履带发生横向挠曲变形，负重轮脱轮时，与诱导齿发生刚体碰撞，相互作用力较大，负重轮被迫沿诱导齿面移动。当诱导齿的高度较高时，负重轮难以脱出诱导齿的束缚，抵抗脱带能力较强，所以当条件一定时，诱导齿的高度较高，负重轮脱带概率较小。

3.3 神经网络拟合及优化分析

神经网络作为新兴的信息处理科学，在许多学科都有着广泛的应用。神经网络在机械工程重的应用，包括在机械设备的运动控制、加工工艺、摩擦学、表面工程、故障诊断、结构优化等方面。BP神经网络采用最小均方误差学习方式，建立从输入到输出的任意非线性映射关系，只需要样本数据[14]。为进一步降低履带脱轮概率，从而对履带刚度、诱导齿、负重轮的参数设计提供指导思路，综合考虑在两种工况下各因素对履带脱轮的影响，将试验结果进行线性叠加。利用神经网络拟合正交试验数据，并对拟合后的表达式进行遗传算法优化，找到履带系统设计变量的最优值。基于GA-BP算法的结构优化设计方法包含2个步骤：1)通过学习样本，建立BP神经网络近似模型，实现设计变量到结构响应的非线性映射；2)通过非线性映射关系，建立基于BP神经网络的数学模型，并通过遗传算法实现全局优化。

BP(Back Propagation)神经网络的训练模式是以误差逆传播的方式，利用最速下降法的学习规则，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。神经元是神经网络中最基本的结构和功能单元，可认为神经网络就是由任意数量的神经元通过不同连接方式组合而成的数学网络模型，BP神经网络的结构如图13所示。

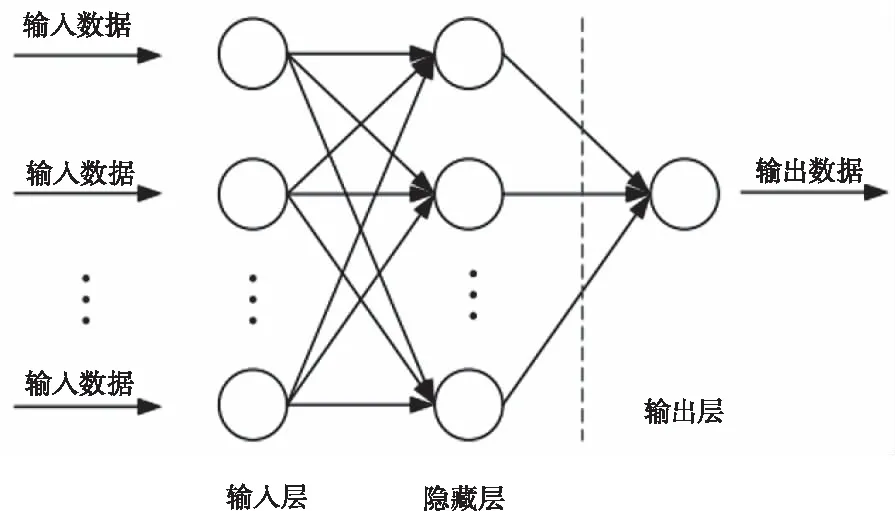
图13 神经网络示意图

BP神经网络通过学习过程得到其模型的结构和权值。学习过程为多层前馈和反向误差修正两个阶段。

前者是指从输入层开始依次计算各层各节点的实际输入、输出；后者是根据输出层神经元的输出误差，沿路反向修正各连接权值，使误差减少。多层前馈数学模型为

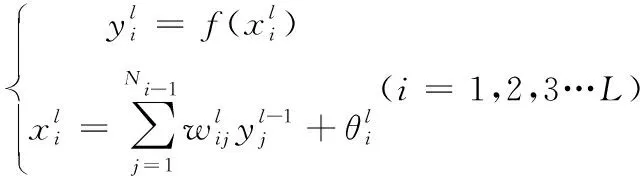
(13)

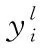
本节基于机器学习框架构建BP神经网络，需设置隐含层层数、各层神经元个数以及神经元激活函数。查阅文献可知，在神经元个数和隐含层层数选择上，尚缺少明确的设定准则，需要根据数据特征进行试算，经验性地进行设置[15]。通过建立的8因素3水平的正交试验表建立神经网络拟合，对拟合后的表达式进行GA算法寻优，找到脱带距离的最大值。本节正交试验中考虑了扭转工况和横推工况下两种情况下的脱轮距离，而履带车辆在行驶过程中，处于复杂工况下，故将扭转工况与横推工况脱轮距离相加，寻优最大值。神经网络输入参数为8个，分别对应正交试验的8个因素，输出为脱轮距离。选取激活函数为Relu，其中27组试验结果随机分为20组训练集和7组检测集，其中训练集和测试集的误差分别如图14图15所示。

图14 训练集预测结果及误差

图15 测试集预测结果及误差

从图中可以看出神经网络拟合效果良好，采用回归系数R2来评定神经网络拟合效果。

(14)

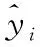
对拟合好的神经网络进行遗传算法优化，优化设计变量为正交试验8个因素，适应度函数为神经网络的拟合函数。遗传算法的迭代进化曲线如图16所示。由图16可以看出随着迭代次数的增加，负重轮可移动的距离逐渐趋于平稳，遗传算法达到收敛值。其中遗传算法优化后各个因素最优取值如表7所示。

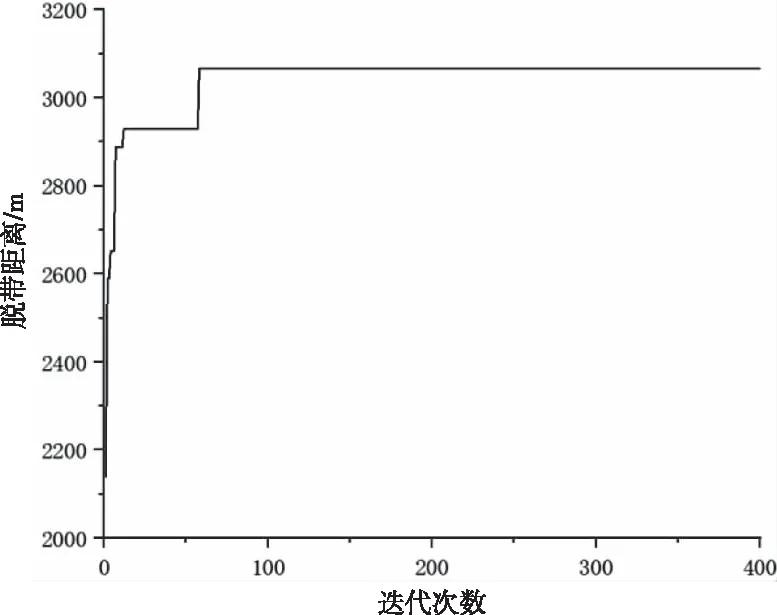
图16 遗传算法迭代图

根据优化后的结果可以看出，履带三个方向的刚度相比于优化前均有不同程度的增大，这也说明刚度越大，履带发生脱轮的概率越小。其中弹簧刚度、诱导齿高度也相应增加，这与上文分析的诱导齿高度越高、弹簧刚度越大，履带发生脱轮概率越小相吻合。将优化后的各个设计参数值带入到拟合的神经网络中，可得到优化后负重轮的行驶距离为3100 mm，相比于初始值，履带系统的运行稳定性可提升36.8%，脱轮概率大幅度下降。

表7 优化变量值

5 结论

为降低履带车辆在行驶过程中履带脱轮发生概率，以试验和仿真为手段充分考虑到实际车辆履带特性参数，并基于多体动力学仿真平台ADAMS搭建了履带脱轮虚拟样机实验台，并由正交试验理论设计了会影响履带车辆脱轮的影响因素试验方案，重点研究了履带刚度、弹簧刚度、诱导齿及负重轮设计参数等对履带脱轮发生概率的影响规律，得到结论如下：

1)从履带脱轮机理出发，分析了履带脱轮时诱导齿与负重轮相互作用力的关系，并建立了履带脱落的条件公式。并由此可得出摩擦系数μ越大，履带发生脱轮的概率越大。α角及负重轮与诱导齿的相遇角β越大，履带发生脱轮的概率也越大。

2)通过对履带脱轮仿真研究可知，不同刚度特性履带、诱导齿及负重轮设计参数对履带发生脱轮难易程度的影响有较大同，其中在扭转工况中，负重轮轮缘角度、弹簧刚度、履带扭转刚度对履带脱轮的影响较为显著，在横推工况中诱导齿高度、履带纵向刚度、负重轮轮缘角度对履带脱轮的影响较为显著。正交试验的设计为今后防止履带脱轮，履带参数化设计提供了理论依据和使用指导。

3)基于正交试验结果利用BP神经网络进行拟合，结果表明拟合效果良好，测试集R2为0.932，满足误差许可。经过遗传算法优化后，履带车的行驶的稳定性提高了36.83%，脱轮概率大大降低。