飞机发动机短舱声传播预计方法研究

薛东文，燕 群，李卓瀚

(航空工业飞机强度研究所航空声学与振动航空科技重点实验室，陕西 西安 710065)

1 引言

过去几十年中，在减少飞机噪声排放方面已经取得了巨大的进步。尽管如此，航空公司和飞机制造商仍然受到居住在机场附近的政府机构和居民的压力，要求进一步降低飞机噪声水平[1]。对于当代大型客机，飞机的主要噪声源是发动机噪声，而在起飞过程中，通过进气道和排气道向外辐射的风扇噪声是发动机噪声的最主要分量。发动机噪声通过进、排气道向外辐射噪声之前受短舱壁面声衬吸声作用，部分噪声被吸收。短舱声衬的成功设计非常依赖于对短舱声传播的预计。

在发动机短舱排气噪声的预测研究中，内、外涵道之间以及外涵道与外界环境之间的剪切流动对声传播的影响通常不可容忽视。一方面，剪切流动会导致声波的发射和散射，改变传播方向；另一方面，剪切流的存在会引起数值上内部动力学不稳定波。当剪切流速度剖面出现拐点时，Kelvin-Helmholtz不稳定波将会被激发。该类型不稳定波以指数形式增长，导致噪声预计失败。

避免Kelvin-Helmholtz不稳定波出现的一种方法是在频域内求解线化欧拉方程[2-4]。对于三维问题，未知数的个数很多，通常采用迭代求解方法。迭代求解等效于采用时间推进格式求解，还是会激发不稳定波[5]。

Kelvin-Helmholtz剪切不稳定波是一种涡结构。由于涡结构的不稳定波很难从控制方程中分离出来，数值不稳定波抑制技术则成为数值计算中消除不稳定波干扰的重要手段。数学上，Kelvin-Helmholtz剪切不稳定波的存在是由于背景流动速度流线剖面中存在拐点。一种不稳定波抑制方法为声源滤波技术(Source Filter，SF)，通过在线化欧拉方程中加入额外的项，以削减不稳定波[6]。然而，SF方法在抑制不稳定波的同时，对声场产生了一定干扰。利用声波和不稳定波传播速度的差异，一种时域波群方法 (Time Domain Wave Packet，TDWP)被用于研究不稳定波的抑制技术[7]，该方法对声波的传播影响较小。

在本文中，一种流动梯度去除方法，即直接去掉线化控制方程中的速度梯度项的方法被用于抑制发动机排气噪声中的K-H剪切层不稳定波的抑制。

本文的研究思路如下：首先，给出文章应用的主控方程，求解方法和边界条件，特别的给出流动梯度去除方法的实现；其次，针对一种公开的发动机进气道研究构型，进行固壁边界条件和声衬边界条件下的声传播预计，初步判定基本预计方法的准确性；再次，针对一种具有解析解的发动机排气噪声预计模型开展声传播预测，验证本文的预计方法在基本的排气噪声研究中的适用性；再次，针对一种产生K-H不稳定波的发动机排气噪声研究模型，开展噪声预测，评估MFGR方法在已知K-H不稳定波中的效果；最后，给出小结。

2 数学模型

2.1 主控方程

通常认为，线化欧拉方程可用于发动机短舱声传播预计[8]。小振幅声波传播的三维线化欧拉方程为

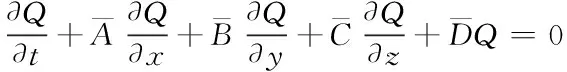
(1)

ρ′，p′，u′，v′，w′分别代表时域内密度、压力及速度扰动分量。下标0表示时均量。

2.2 边界条件

本文研究模型声衬的前、后端为声学固壁，即声学全反射，在声学固壁表面法向声质点速度为0，即

v·n=0

(2)

声衬对声学的作用可以用声阻抗边界来体现。对于局域反应声衬，Ingard给出了声阻抗边界的表达式[9]，可以进一步推导为

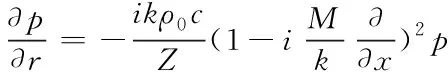
(3)

声学计算的远场边界应用完全匹配层边界条件，声源位置应用模态边界条件。

2.3 流动梯度去除方法

3 数值计算

3.1 飞机发动机短舱进气道声传播计算

JT15D系列航空发动机是普惠公司研制的第一代涡轮风扇发动机。在上世纪70年代NASA Lewis实验室和Langley实验室针对JT15D开展了一系列实验和测试，来研究风扇噪声的传播特性[10]。其实验结果可以为数值模拟提供校核数据。

其静地测试进气道如图1所示。风扇转速为6750rpm，对应一阶叶片通过频率为3150Hz，可传播的主要模态为(-13，0)。分别对未安装声衬和三种不同穿孔率的声衬进行远声场测试，表1给出声衬的声阻抗和相应的穿孔率。

图1 JT15D静地测试进气道示意图

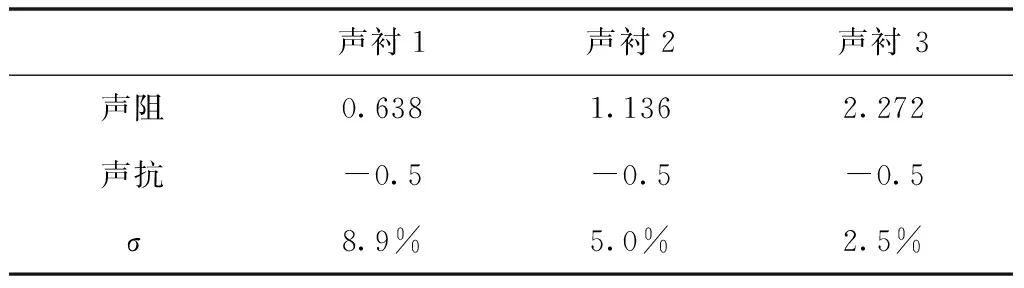
表1 JT15D声衬声阻抗

考虑到该算例为短舱进气道模型，不存在剪切流，因此在主控方程的计算中不做不稳定波抑制处理。直接应用第二节给出的数值方法进行声传播计算，验证方法的正确性。

图2和图3分别给出了进气道在固壁边界和声衬1边界作用下的声传播云图，可以看出声模态在声源面处被加载，噪声沿进气道贴壁向外辐射，在声学远场边界处未发生明显反射；声衬作用下，进气道的远场噪声辐射明显减弱。

图2 固壁边界下的声传播云图

图3 声衬1边界下的声传播云图

图4给出了远场指向性的数值仿真与试验对比，数值仿真结果很好的预计了远场声压分布趋势；在声压分布绝对值方面，声衬边界条件下数值预计的声压略低，误差在3dB以内。这也证明了本文所采用的计算方法和设置可应用于带阻抗边界的、短舱进气道噪声声传播的预计。

图4 数值预计与试验的指向性对比

3.2 短舱后传声解析验证算例

3.2.1 Munt圆形管道固壁解析算例

Munt模型及其演化模型已经形成标准算例，在应用数值方法预计发动机排气噪声时，往往首先计算Munt模型问题，分析和理解问题的物理机理，验证数值计算方法。

图5给出了计算选取的几类Munt简化模型。需要指出的是M1是外界环境流速，M2是管道内流速，R1是涵道外表面半径，R2是涵道内表面半径。表2给出了各个物理量的值。这里一共包含3个简化模型：圆柱形管道模型；环形管道模型；环形管道带阻抗边界模型。模型轮毂是无限长的。可以发现管道内外流速不同，将在管道末端形成剪切涡层。远场指向性测量点位于以管道末端为圆心的、半径为46米、角度范围为0～120°的位置。无量纲化阻抗为2-i，阻抗边界的位置位于涵道下表面(轮毂表面)、外管壁起始至无限远处。

图5 Munt模型及其变形

表2 简化模型物理参数

图6为圆柱形管道模型的声传播压力云图。可以发现，管道内的声模态通过管道末端时，没有明显的不稳定波出现。说明不稳定波被抑制了。声模态在管道末端发生衍射。

图6 圆柱形管道模型近场声压分布云图

进一步分析远场指向性，如图7所示，在远场40°～100°范围内出现3个波峰，形成噪声最强的位置。对比本文计算的结果与南开普敦(ISVR)解析计算的结果[11]进行了对比，可以发现两者在角度和量值上都很好吻合，准确捕捉了远场噪声分布规律，并且准确评估了声压级。最大声压级误差出现在第一个波峰位置，误差约为3dB。角度误差很小，约小于2°。

图7 圆柱形管道声传播远场指向性对比

3.2.2 Munt圆形管道声衬解析算例

图8为轮毂带阻抗边界条件下的声传播压力云图。可以发现，管道内的声模态通过管道末端时，没有明显的不稳定波出现。说明不稳定波被抑制了。声模态在管道末端发生衍射，沿下游且向上传播，主要声能分布在一定角度范围内，0°方向的声能最弱。

图8 环形管道、带阻抗边界声传播

进一步分析远场指向性，如图9所示。相比于不带阻抗边界的环形管道，主要有3点不同：

a) 主要波瓣的声压级降低5dB，主要波瓣的角度位置并未发生变换；

b) 相比固壁的轮毂，紧邻主要波瓣的波谷消失；

c) 相比固壁轮毂模型，在远场80°～150°方向，声压级降低。

总体来讲，加入阻抗边界后，远场辐射噪声明显降低。

图9 带阻抗边界声传播远场指向性对比

同时图9给出了强度所计算结果与TUE计算的解析解[12]对比，发现两者吻合的相当好，指向性分布趋势相符，主要波瓣角度精确相符，声压级最大偏差小于3dB，主要波瓣位置声压级误差小于2dB。说明本文所采用的计算方法和设置可应用于带阻抗边界的、简单排气噪声模型的计算。

3.2.3 TURNEX双涵道后传声算例

TURNEX (Turbomachinery Noise Radiation through the Engine Exhaust)项目是欧盟FP6框架下研究发动机排气噪声的项目[13]。该项目发展了一些几何模型和工况用于不同数值算法之间的对比。图10给出了TURNEX项目中短涵道几何模型。

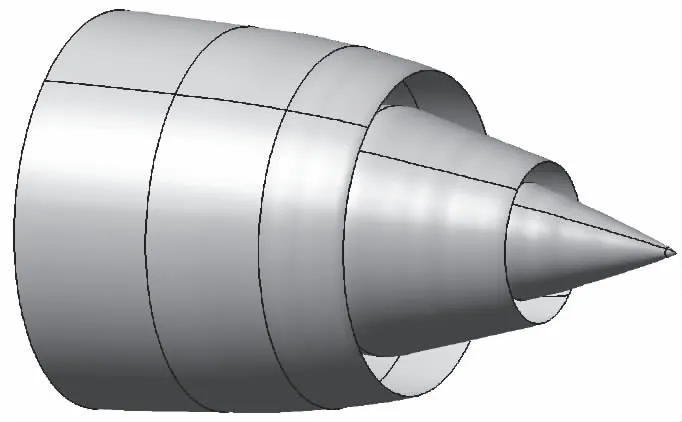
图10 排气道外形轮廓

表3主要是气动参数，给出了内、外涵声速、温度、密度、马赫数等信息。

表3 气动参数表

图11为(9，0)模态下声压分布云图，图12为其指向性分布。可以看出，在外涵道上表面的末端出现了不稳定波，该工况下不稳定波现象较弱，不至于影响计算的收敛。此次计算中并没有去除主控方程当中的速度梯度项。将本文计算的结果与Andrea lob高精度计算的结果[14]进行对比，两者在主要波瓣的角度、幅值方面吻合的都相当好，角度误差不大于3°，最大误差不大于3dB。这种误差的来源之一是由于参考文献中没有给定声源幅值，本文给定的声源幅值只能做有限且近似的调整。两者的对比在轴线方向有一些偏差，本文计算的结果出现了一个小量值的波瓣，这个值相当小，可以忽略。

图11 (9，0)模态的声压云图

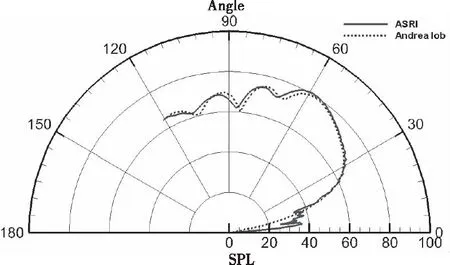
图12 (9，0)模态的远场指向性分布

图13、图14为(0，0)模态下声压分布云图，图15为其指向性分布。在图13的计算中没有去除主控方程当中的速度梯度项，在外涵道上表面的末端出现了很强的不稳定波。该结果是计算过程中某一时刻的声压分布，可以看出，声压的最大值出现在的管道末端不稳定波位置，幅值特别大。这种不稳定波最终导致了计算的发散。说明对于有流工况下(0，0)阶声模态作用下的声场计算，必须降低不稳定波的影响。图14的计算中去除主控方程当中的速度梯度项，可以看出在外涵道上表面的末端的不稳定波消失。将本文计算的结果与Andrea lob高精度计算的结果进行对比，两者在主要波瓣的角度、幅值方面吻合的都相当好，角度误差不大于3°，最大误差不大于3dB。这种误差的来源之一是由于参考文献中没有给定声源幅值，本文给定的声源幅值只能做有限且近似的调整。由于在Andrea Iob的文献中并没有提出其远场指向性的中心点具体位置，本文的圆心定位可能与其不同，这也可能是导致远场指向性有偏差的主要原因。

图13 (0，0)模态的声压云图-不稳定波

图14 (0，0)模态的声压云图

图15 (0，0)模态的远场指向性分布

4 小结

文章针对飞机发动机短舱的声传播预计方法开展研究。应用有限元方法求解时域线化欧拉方程方程，用Ingard边界条件模拟声衬；应用流动梯度去除方法抑制发动机排气道噪声预计中产生的Kelvin-Helmholtz不稳定波。针对飞机发动机短舱进气道噪声、排气道噪声在有/无声衬作用下的声传播开展了预测，通过与国际上公开的试验结果进行了对比，结果表明：

1) 本文给出的短舱声传播预计方法可用于短舱进气道声传播预计，远场指向性的声压级误差低于3dB；

2) 本文给出的基于背景流场速度梯度去除的方法可用于剪切流中不稳定波的抑制；

3) 声源为低阶声模态时更容易出现K-H不稳定波，声源为高阶声模态时出现的K-H不稳定波较弱，不影响声场计算；

4) 本文给出的短舱声传播预计方法可用于短舱排气道声传播预计，远场指向性的声压级误差低于3dB，指向性角度误差小于3°。