石灰改良红黏土导热系数影响因素及模型预测
2023-03-27王红旗李栋伟钟石明贾志文王泽成陈鑫秦子鹏
王红旗,李栋伟*,钟石明,贾志文,王泽成,陈鑫, 秦子鹏
(1.东华理工大学土木与建筑工程学院,南昌 330013; 2.浙江水利水电学院水利与环境工程学院,杭州 310018)
红黏土作为一类特殊土,广泛分布于中国南部、东部等气候湿热的地区,在江西等地也有较为广泛的分布[1];因其天然含水率高、孔隙比大、易成团、弱酸性、吸水软化、失水开裂等特点[2],一般不被直接应用于路基回填。由于红黏土具有较强的水敏性等特点,经常采用价格低廉、吸水性强、对土体改良有较好效果的石灰、水泥对其进行改良。在红黏土的改良中,石灰改良红黏土,改变了土体结构及组分,在一定程度上提高了红黏土强度。但是,由于红黏土吸水软化,具有团粒效应,在土体改良过程中很难进行均匀搅拌,且生石灰遇水呈碱性,与弱酸性的红黏土之间存在酸碱作用,容易导致石灰对红黏土的改良效果受到土体团粒尺寸、酸碱作用等因素的影响,出现改良效果不佳的现象[3]。已有工程实例表明,石灰改良红黏土工程在投入使用后出现破损、渗漏等问题[4]。谈云志等[5]基于石灰改良红黏土的酸碱作用,揭示了石灰与红黏土的互损机理,解释了石灰改良红黏土工程投入使用后,受季节性气候以及雨水等作用下,路基工程出现问题的原因[3-4],提出了偏高岭土减损的机制。
可见,在石灰改良红黏土路基中,石灰与红黏土之间的互损作用在气候、雨水以及外荷载等多种因素的共同作用下使得路基改良土的应力场、温度场发生了改变。石灰与红黏土之间存在的互损作用时间越长,路基破坏积累就愈发严重,前人从应力场对其进行了研究,以降低红黏土对石灰处治红黏土的影响,针对石灰改良红黏土温度场的研究还较为少见。而导热系数是研究温度场的重要参数,因此,对石灰改良红黏土导热系数的研究具有重大意义。
目前,很多学者对土体导热系数进行了广泛研究,发现导热系数受含水率、干密度、物质组成等多种因素的影响。Nikiforova等[6]通过对不同土壤类型的热物理特性进行研究,并开发土壤热导率的测定方法,得到了不同类型(砂、黏、壤土)土壤的导热系数与湿度的解析相关性;陈波等[7]以桂林红黏土为例,研究了红黏土在脱湿过程的导热系数演化规律,采用Lu模型等对导热系数进行预测,表现出了较为良好的预测效果。谢正鹏[8]通过研究干密度、含水率以及红黏土掺量对膨润土-红黏土混合土体的导热系数的影响,总结出了混合材料导热系数影响因素的变化规律;曾召田等[9-10]利用探针法研究了含水率、干密度和土壤质地对粉土、细砂以及4种广西红黏土热导率的影响,分析了土体热导率随影响因素的变化规律和机理;徐云山等[11、王叶娇等[12]采用KD2 Pro测试了黏土在较广温度、含水率范围下土体导热系数的变化规律。
关于土体导热系数的研究,国内外众多学者在研究影响因素的基础上提出了导热系数的经验预测模型。Rubin等[13]基于现有导热系数数据库提出了半分法解析理论模型,研究收集了大量土壤导热系数数据,建立了新的数据库;熊坤等[14]通过利用多种土壤导热系数实测值和与Campbell、Johansen等导热系数模型计算值进行比较和修正,通过精准的预测其他多地土壤导热系数,给出了较为精准的模拟预测模型;张楠等[15]通过对导热系数影响因素的分析,总结了国内外热传导模型的研究现状,对模型的优缺点进行了分析评价。众多研究者基于人工智能算法研究了含水率、矿物组分、温度等多种影响因素研究了岩土体导热系数的变化规律,提出了准确率较高的智能预测模型[16-21]。
目前土体导热系数及模型的研究多集中于含水率、孔隙度、土壤质地等因素影响下的分析预测,然而在改良特殊土导热系数的研究上较少,在石灰与红黏土酸碱互损随时间变化对导热系数影响及多种影响因素下改良土导热系数的预测上还有待于研究。
现通过研究常温条件下石灰改良红黏土在含水率、干密度和龄期等因素影响下,改良土导热系数的变化规律,建立多种影响因素共同作用下的经验预测模型和反向传播(back propagation,BP)神经网络预测模型,以期为红黏土等特殊土及其改良土温度场的研究提供参考。
1 试验材料及方案
1.1 试验材料
试验所用红黏土取自南昌某在建小区工地旁路边,其基本物理参数如表1所示,关于红黏土的基本物理参数的测定具体过程见《土工试验方法标准》(GB/T 50123—2019)[22]。试验使用的生石灰,购买于江苏南京惠灰牌高纯度生石灰,其含钙率高达99%,试验用石灰粒度小于0.5 mm。

表1 红黏土的基本物理参数Table 1 Basic physical parameters of red clay
1.2 试验方案
前人研究发现,石灰掺量为5%~7%时[23-25],改良土的力学性能最佳,本试验以6%的石灰掺量,研究干密度、含水率、龄期等因素对石灰改良红黏土导热系数的影响,以最优含水率、最大干密度为基准设置含水率、干密度的范围。具体试验方案如表2所示。
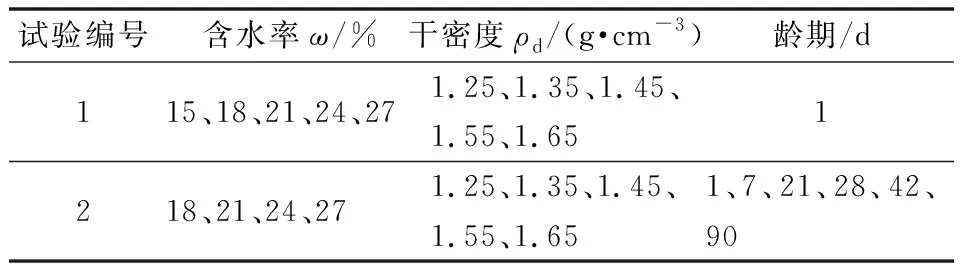
表2 试验方案Table 2 Test plan
试验1研究含水率、干密度对改良土体导热系数的影响;试验2研究不同含水率、干密度下导热系数随龄期的演化规律,由于含水率27%、干密度1.65 g/cm3无法制样,为保证拟合公式模型精度较高,向前递补含水率27%、干密度为1.25 g/cm3试样进行规律的研究;试龄期7 d和21 d试验数据仅用于经验公式验证数据。
1.3 试样制备
将天然状态下收集的红黏土进行自然风干、破碎处理,然后过0.5 mm筛后放入烘箱进行烘干,设定105 ℃,烘12 h,待冷却后,放入密封保鲜袋内保存备用。
按照预测的含水率、干密度称取石灰、红黏土,先进行干土均匀混合搅拌,再添加水进行再次搅拌,搅拌全程在塑料袋内密封进行,防止搅拌过程水分等的流失,搅拌均匀后静止24 h,待混合土体水分分布均匀,称取试样所需的土量,精确至0.01 g,置于规格为Φ61.8 mm×20 mm、容积60 cm3的制样模具中,压制成标准试样,并立即采用多层保鲜膜进行密封保存,随后将试样集中放入样品保存箱中进行试样的常温(室温)保存,等待试验测样。如图1所示为试验制样保存过程。

图1 试验制样保存过程Fig.1 Storage process of test sample preparation
1.4 试验仪器
改良土导热系数试验采用XIATECH TC3000E瞬态热线法便携式导热系数仪,该导热系数仪器的导热系数量程为0.005~10 W/(m·K),使用温度范围较广,最低温度可达-60 ℃,最高温度为120 ℃,误差为±3%,试验仪器如图2所示。

图2 试验仪器Fig.2 Test instrument
完成相关仪器设定并进行仪器稳定性检测,待仪器工作稳定后开始进行导热系数测量。
2 试验结果与分析
2.1 含水率对导热系数的影响
含水率是土体重要的物理参数之一,影响着土体的多种物理性质。图3为石灰改良红黏土在相同干密度下,导热系数λ随含水率变化关系拟合曲线。
由图3可知,在相同干密度下,改良土体的导热系数随含水率的增大逐渐增大。在含水率15%~27%范围内,干密度为1.25~1.65 g/cm3的改良土导热系分别增加了0.417 2、0.476 2、0.492 3、0.441 5、0.391 0 W/(m·K),平均增比53.87%。
随着改良土体的含水率增大,土体内部孔隙被水充填,使得土体孔隙中空气体积减少,原孔隙被水充填,空气导热系数[0.024 W/(m·K)]小于水的导热系数[0.605 W/(m·K)][10],因此在一定的含水率范围内,改良土体导热系数随着含水率的增大,土颗粒间的水膜增大,孔隙减小,导热面积增加,土体的导热系数增加。由图3中拟合曲线可知,改良土的导热系数随含水率的增加,增幅逐渐降低,土体的导热系数有趋于稳定的趋势,导热系数随含水率变化关系高度符合指数分布。
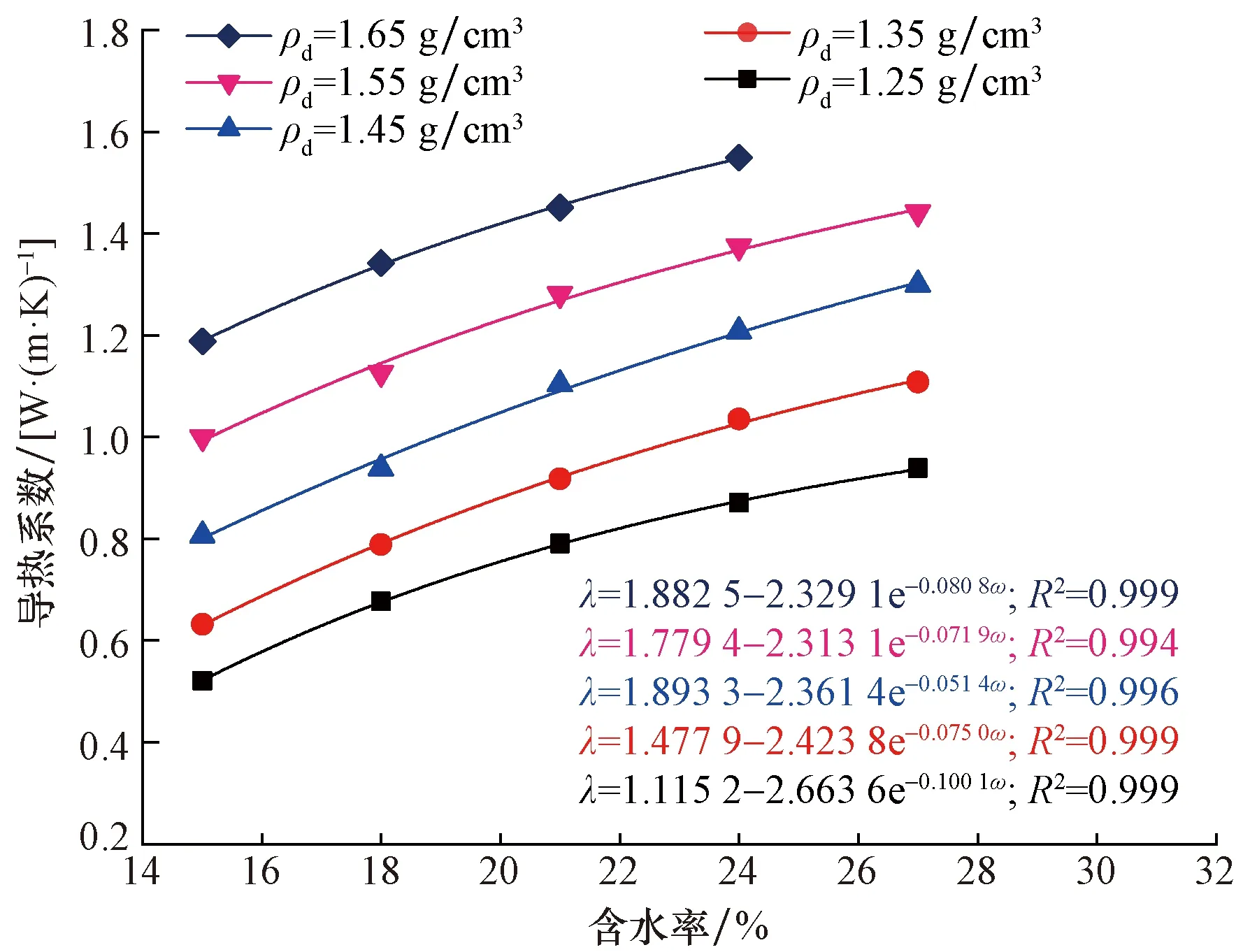
图3 导热系数同含水率关系拟合曲线Fig.3 Fitting curve of relation between thermal conductivity and moisture content
2.2 干密度对导热系数的影响
干密度是土体重要的物理因素之一,图4为不同干密度、相同含水率情况下,改良土体导热系数随干密度变化拟合曲线,可以看出,在含水率相同时,石灰改良红黏土混合土体导热系数随着干密度的增加逐渐增大,在干密度为1.25~1.65 g/cm3范围内,含水率为15%~27%的石灰改良红黏土土导热系数分别增加了0.636 8、0.664 8、0.660 7、0.677 8、0.502 6 W/(m·K)。平均增比87.06%,随着含水率增加,改良土导热系数随干密度增幅逐渐降低。
随着干密度的增加土体密实度增加,颗粒间孔隙变小,颗粒间接触面积变大,接触更加紧密,土体孔隙减小,减小部分孔隙被黏土颗粒充填,导热面积增加,由于土颗粒的导热系数大于空气的导热系数[土颗粒和空气导热系数分别为2 W/(m·K)]和0.024 W/(m·K)[10],因此土体导热系数会随着干密度的增大而增大,且由图4中拟合曲线可知,改良土体导热系数随干密度变化高度符合线性增长。
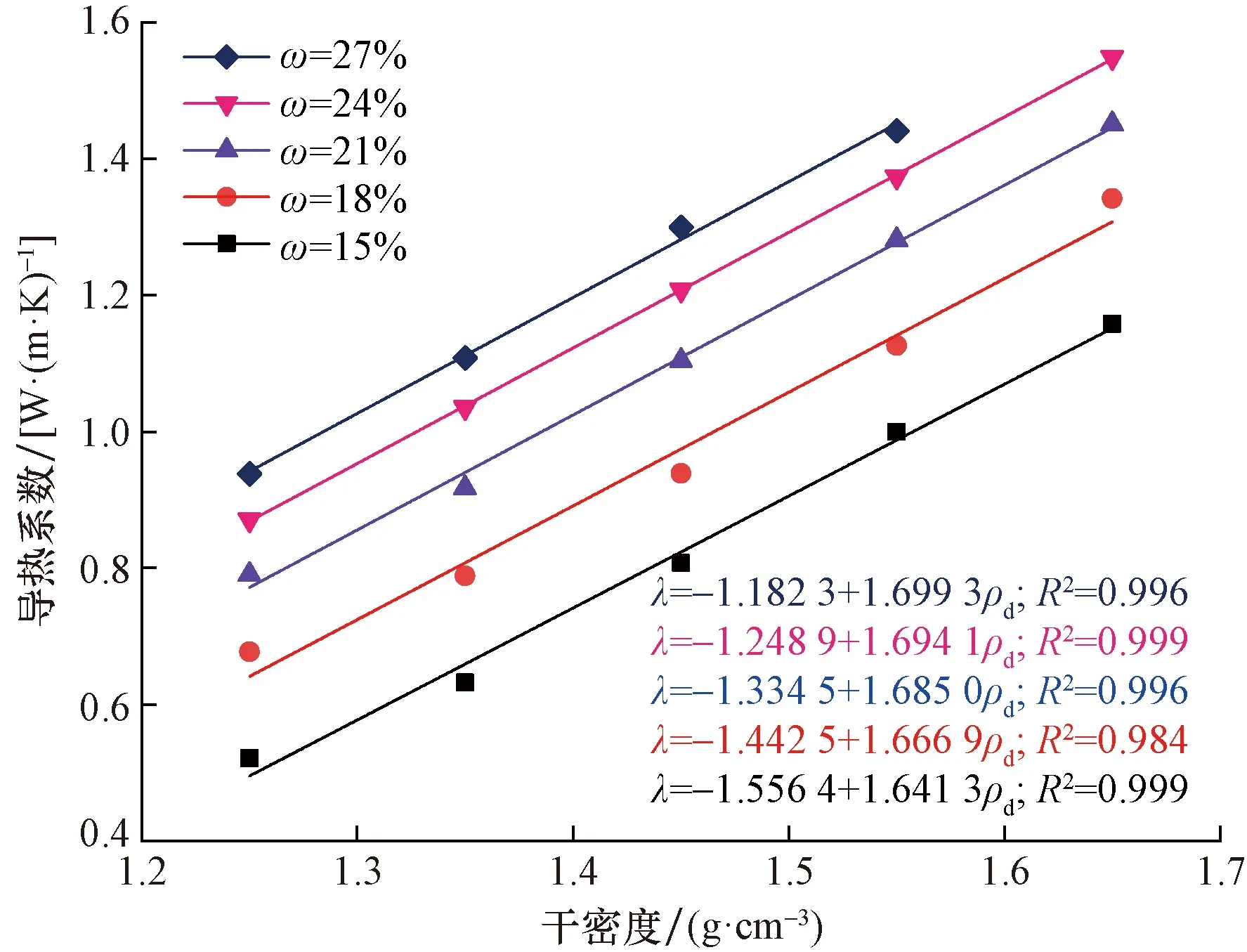
图4 导热系数随干密度变化拟合曲线图Fig.4 Fitting curve of thermal conductivity with dry density change
由导热系数同干密度关系回归公式可知,随着含水率的增大,导热系数随干密度的增加速率在增大,可见石灰改良红黏土土体的导热系数受含水率及干密度共同影响,且影响形式不同。
2.3 龄期对导热系数影响
图5所示分别为在含水率为18%~27%,不同干密度情况下导热系数随龄期变化拟合曲线;可以看出,在龄期达到90 d时,含水率为18%,干密度分别1.35~1.65 g/cm3时,改良土导热系数分别降低了0.193 8、0.222 3、0.252 9、0.266 0 W/(m·K),平均降低22.67%;含水率为21%,干密度为1.35~1.65 g/cm3时,改良土导热系数分别降低了0.171 9、0.194 4、0.205 0、0.225 0 W/(m·K),平均降低16.82%;含水率为24%,干密度分别为1.35~1.65 g/cm3时,改良土导热系数分别降低0.156、0.179 9、0.185 0、0.223 0 W/(m·K),平均降低14.45%;含水率为27%,干密度分别为1.25~1.55 g/cm3时,改良土导热系数分别降低了0.135 5、0.131 6、0.160 5、0.160 9 W/(m·K),平均降低12.46%;在龄期90 d范围内,导热系数整体平均降低16.6%。结合导热系数随龄期变化关系拟合曲线可以看出,导热系数随龄期变化呈指数性降低,最终有趋于稳定的趋势。
图5 不同含水率下,导热系数随龄期变化曲线Fig.5 Curves of thermal conductivity changing with age at different moisture content
可见,含水率、干密度以及养护龄期共同影响着石灰改良红黏土的导热系数,在含水率15%~27%范围内,改良土导热系数随含水率呈指数增加,在含水率范围内,导热系数整体平均增幅53.87%;在干密度为1.25~1.65 g/cm3范围内,导热系数随干密度呈线性增长,在干密度范围内整体平均增长87.06%;在龄期1~90 d范围内,导热系数随龄期呈指数降低,在龄期范围内,改良土导热系数整体平均降低16.6%。因此,在含水率(15%~27%范围内)、干密度(1.25~1.65 g/cm3)范围内以及龄期(1~90 d范围内)等因素影响下,干密度对改良土的导热系数影响最为显著,龄期对改良土体导热系数影响较小。
3 预测模型
3.1 常用预测模型
关于预测模型,众多学者提出了针对不同影响因素的土体导热系数预测模型,同时也有部分学者在前人模型的基础进行了分析验证,并对其加以修正改进,提出了影响因素众多、普适性更强、精确度更高的修正模型,常用的几种预测模型[10,14-15]如下。
3.1.1 Kersten模型
Kersten模型[26]是一种基于温度、含水率、饱和度、干密度等多种因素所提出的一种适用范围较广的经验预测模型,具体形式为
K=0.144 2(0.9lgω-0.2)×100.624 3ρd
(1)
式(1)中:K为土的导热系数;ω为土的含水率,%;ρd为土的干密度,g/cm3。该公式适合于粉土或黏土。
K=0.144 2(0.7lgω+0.4)×100.624 3ρd
(2)
该公式适用于砂性土。
3.1.2 Johansen模型
Johansen模型[27]是在Kersten模型的基础上的进一步综合多因素提出归一化模型,表达式为
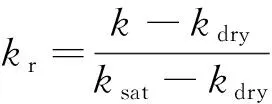
(3)
式(3)中:kr为归一化导热系数;ksat、kdry分别为饱和土和干土状态下土体的导热系数。同时,Johansen还通过优化他人的公式模型进一步提出了改进后的导热系数预测模型。
(1)当土体为干土状态时。
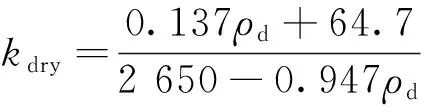
(4)
(2)当土体处于饱和状态时。
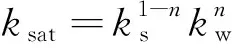
(5)
式(5)中:ks、kw分别为固体土颗粒、孔隙水的热导率;n为孔隙率。
(3)当土体处于未饱和状态时。
kunsat=(ksat-kdry)ke+kdry
(6)
式(6)中:ke为Kersten模型中的计算公式,ke=lgsr+1.0,Sr为土体饱和度。
3.1.3 采用几何均值算法的Kersten模型
当将土体视为固、液、气三相组成的物质时,采用几何均值算法的Kersten模型。
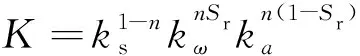
(7)
3.1.4 Donzzi模型[28]
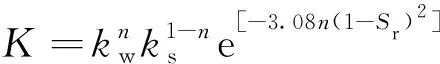
(8)
3.1.5 有效介质理论模型[9]
串并联模型是基于三相组成的常用的介质理论模型。
(1)并联模型。
ke=νaka+νbkb+νckc
(9)
式(9)中:ki、vi分别为土体中固、液、气三相对应的导热系数以及所占体积分数,i=a,b,c。
(2)串联模型。
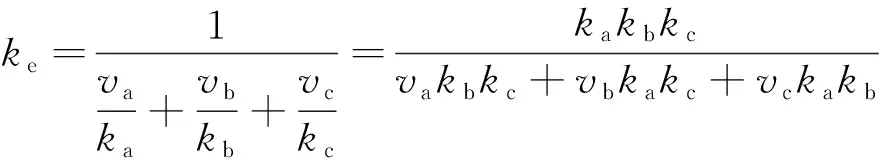
(10)
3.2 导热系数随含水率、干密度、龄期变化经验模型
根据龄期对导热系数的影响以及结合含水率和干密度对石灰改良红黏土导热系数影响,拟合归纳出石灰改良红黏土导热系数随龄期、含水率、干密度变化预测公式模型如式(1)所示,具体为
λ=y0+AeRt
(11)
A=(a1ρd+b1)ω2+(a2ρd+b2)ω+a3ρd+b3
(12)
R=(c1ρd+d1)ω2+(c2ρd+d2)ω+c3ρd+d3
(13)
y0=g1ω2+(g2ρd+f1)ω+g3ρd+f2
(14)
式中:λ为导热系数,W/(m·K);ρd为干密度,g/cm3;ω为含水率,%;t为龄期,d。其他相关参数具体值如表3所示。
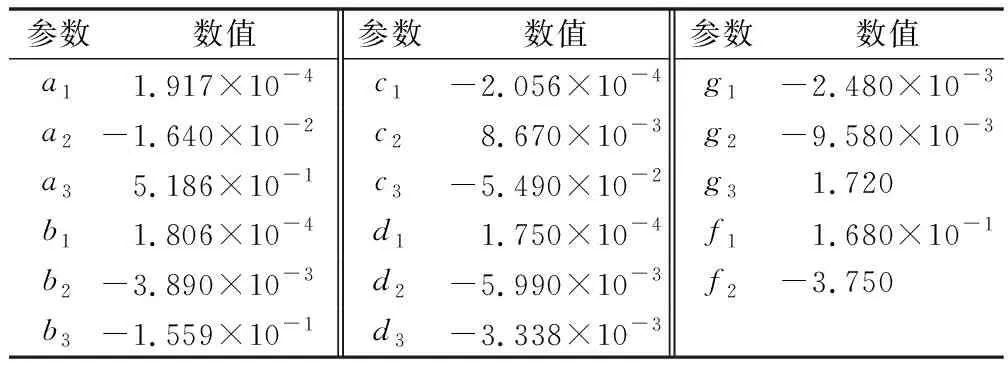
表3 拟合公式其他相关参数表Table 3 Other related parameters of the fitting formula
3.3 BP神经网络预测模型
BP神经网络模型是一种将计算输出误差反向传递并向前反馈的一种智能神经网络算法,通过将误差向前反馈以降低计算误差,提高预测精度,在非线性计算和多维函数映射上具有较高的适用性[17]。结构上一般分为3层:输入层、隐藏层、输出层;其中隐藏层又可以设置为多层隐藏层。图6为BP神经网络结构示意图和流程图。在BP神经网络中,第一层输入层包含3个神经元;第二层隐藏层,采用的是双层隐藏结构,神经元个数分别为6、3;第三层输出层为1个神经元;采用了速度更快,更便捷的随机梯度下降(stochastic gradient descent,SGD)法;激活函数采用的是Relu函数;将所有试验数据进行七三分,分别进行模型的训练和测试,最大迭代次数为2 000次,初始学习率为0.04。
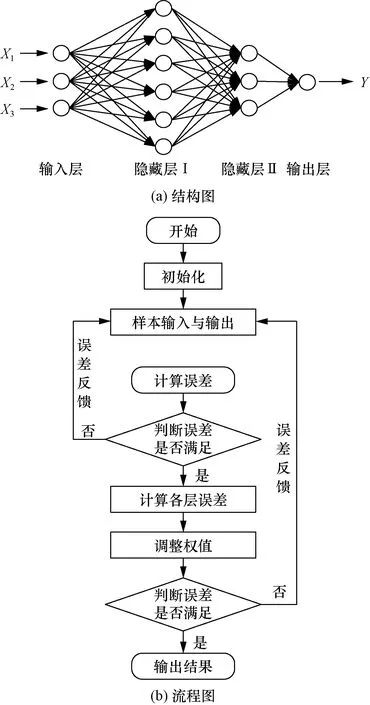
输入层中,X1、X2、X3分别为含水率、干密度、龄期;输出层中,Y为改良土导热系数图6 BP神经网络结构示意图和流程图Fig.6 BP neural network structure diagram and flow chart
如图6(b)流程图,通过将试验数据读取,完成数据初始化处理,进行样本的输入与模型计算后输出,判断误差整体误差是否满足需求,不满足要求的数据进行误差反向传播,满足要求的进行逐层误差分析、调整权值并再次判断,如误差不满足需求进行误差的再次前馈,最终完成模型预测。表4为BP神经网络预测值和实测值误差分析。

表4 BP神经网络预测值和实测值误差分析Table 4 Error analysis of BP neural network predicted value and measured value
通过BP神经网络预测值与实测值进行对比发现,BP神经网络预测模型,预测误差最小0.03%,最大为4.68%,BP神经网络预测数据的均方误差(mean square error,MSE)为0.000 2;对土体导热系数预测效果较好。
3.4 模型的对比验证与分析
图7为不考虑龄期时,多种预测模型同新预测模型预测数据误差分析,通过预测数据分布,可以清晰看出,新预测模型对黏土体导热系数的预测效果最佳,95.83%的预测值误差10%以内,4.17%的预测值误差在10%~20%;Kersten模型预测值误差在10%以内的占62.5%,约12.5%的预测值误差超过20%;Johansen模型的预测值中约29.17%的预测值在10%以内,约70.83%的预测值误差大于10%;并联模型约37.5%的预测值误差小于10%,62.5%的预测值误差超过20%;串联模型、Donzzi模型和采用三相均值计算方法的Kersten模型预测值误差大于20%;新经验预测模型的精准度最高,其次是Kersten模型,其他模型的预测误差均偏差较大,新模型、Kersten模型的均方根误差(root mean squared error,RMSE)[29]分别为0.064 7和0.111 6;平均误差百分比(mean absolute percentage error,MAPE)值分别为5.87%和10.40%;可见新预测模型和Kersten模型均属于预测精度较高的模型,但相较之,新预测模型的预测精度更高。
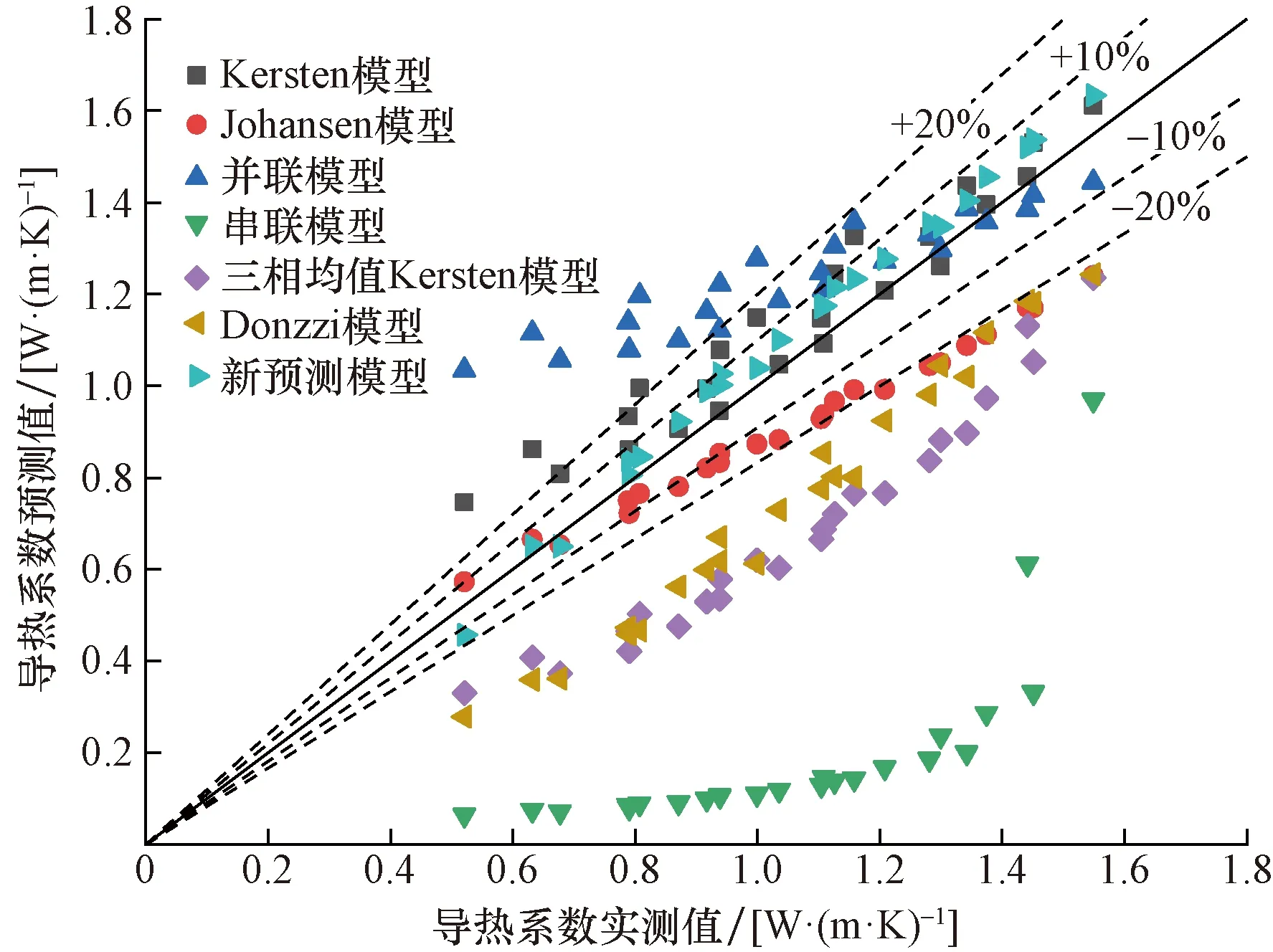
图7 不考虑龄期时各种模型预测误差分析Fig.7 Prediction error analysis of various models without considering ages
如图8(a)、图8(b)所示分别为龄期7 d和21 d时,龄期对石灰改良红黏土导热系数影响模型预测误差分析,可以看出,龄期7 d、21 d时新模型预测值与实测值之间误差均低于10%;龄期7 d预测数据的RMSE和MAPE值分别为0.067 0和5.77%;龄期21 d预测数据的RMSE和MAPE值分别为0.063 2和6.32%综合以上,新预测模型对石灰改良红黏土导热系数随龄期变化的预测精度较高。
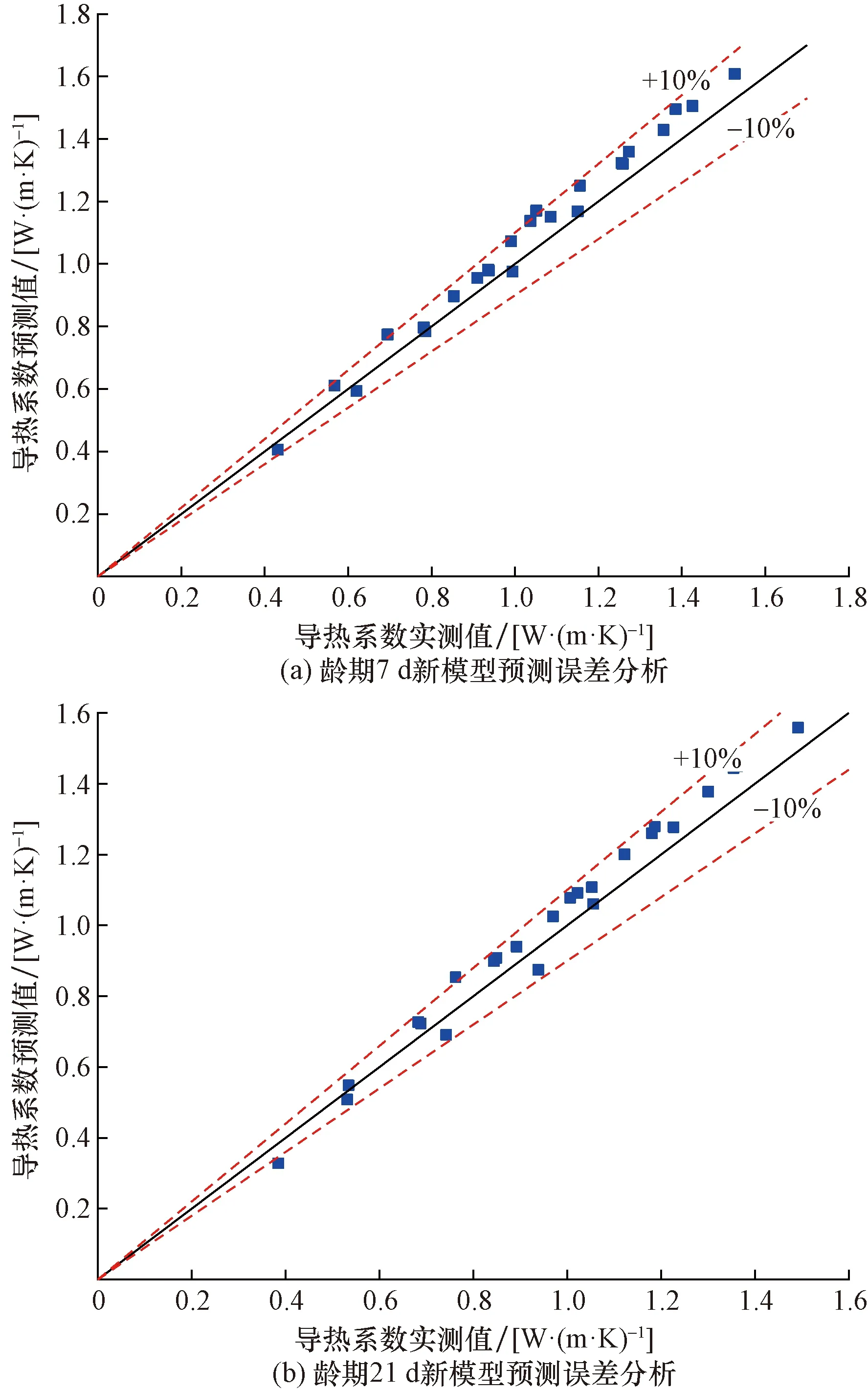
图8 龄期对导热系数影响模型预测误差分析Fig.8 Model prediction error analysis of influence of age on thermal conductivity
图9为石灰改良红黏土的BP神经网络模型预测误差分析。结合BP神经网络模型的预测值和导热系数实测值,可知,BP网络预测模型可以很好地实现石灰改良红黏土导热系数随龄期、含水率、干密度的变化关系,模型整体预测RMSE值和MAPE值分别为0.012 6和1.73%,BP神经网络模型对改良土导热系数实现了较为精准的预测。
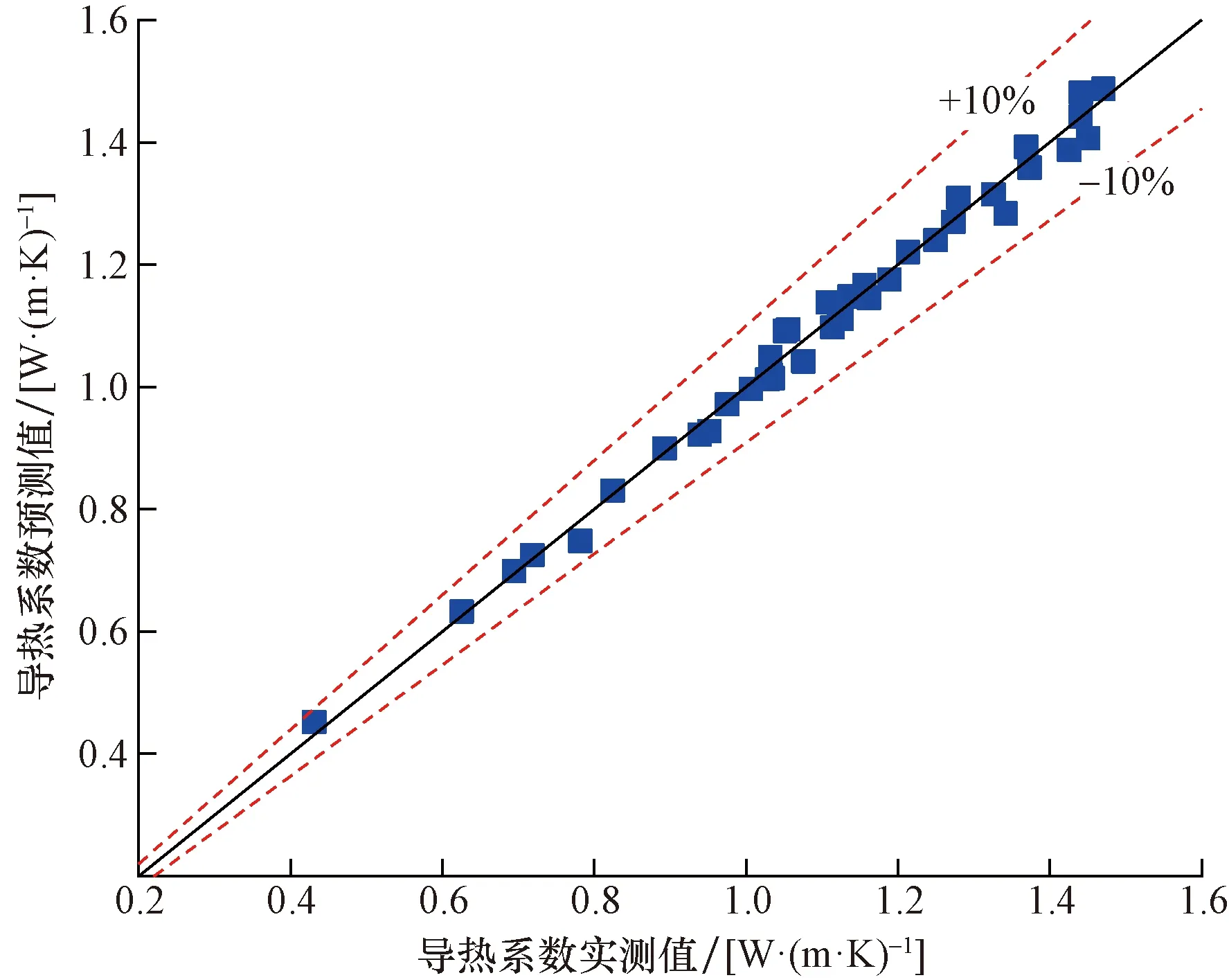
图9 BP神经网络模型预测误差分析Fig.9 BP neural network model prediction regression curve
可见,新经验模型和BP神经网络预测模型考虑了物质间相互作用对导热系数的影响,可以很好地实现含水率、干密度以及龄期等因素影响下石灰改良红黏土导热系数的精准预测。
4 结论
通过研究含水率、干密度以及龄期对石灰改良红黏土土体导热系数的影响及变化规律,并提出相关预测模型,得出以下结论。
(1)石灰改良红黏土导热系数随含水率的增加逐渐增大,平均增比53.87%,且随含水率的增加,导热系数的增幅逐渐降低,导热系数最终有趋于稳定的趋势,整体拟合曲线呈指数分布;在相同含水率情况下,导热系数随干密度增大而增大,平均增比87.06%,整体拟合曲线呈线性分布。
(2)石灰改良红黏土导热系数随养护龄期的增加逐渐降低,整体平均降低16.6%,降低速率随着龄期增大逐渐减小,最终有趋于稳定的趋势,拟合曲线整体呈指数性分布。
(3)当不考虑龄期时,新预测模型同Kersten模型相似,同属于在含水率、干密度两个影响因素共同作用下对土体导热系数进行预测的经验模型,经过误差分析,新预测模型的RMSE和MASE值分别为0.064 7和5.87%,较之常见的几种预测模型,预测精度更高。
(4)新经验模型和BP神经网络预测模型考虑了物质间的相互作用伴随龄期对改良土导热系数的影响,针对性更强,精度更高,经过误差分析,新预测模型和BP神经网络模型的RMSE较小,且MASE值均低于10%;BP神经网络预测模型预测效果最佳、精度最高,普适性更强。
