基于深度学习技术的金属构件残余应力场反演
2023-03-27王璐熊土林马沁巍刘广彦张笃周
王璐,熊土林,马沁巍,刘广彦*,张笃周
(1.北京理工大学宇航学院,北京 100081; 2.中国空间技术研究院,北京 100094)
金属材料在锻造、切割等加工工艺中会不可避免地引入残余应力,残余应力的存在则会显著地影响材料的屈服极限、抗拉及抗压强度等力学性质[1-4]。因此,准确地获取材料/结构的残余应力分布对确保材料/结构的安全至关重要。实验测试法是目前最常用的获取材料/结构表面残余应力分布的方法,基于是否需要对材料进行破坏,实验测试法可以分为破坏性实验法[5-6]及非破坏性实验法[7-8]。破坏性实验法可以通过试件破坏后的变形程度计算出残余应力,该方法具有较高的计算精度并且可以实现构件内部残余应力的计算,但无法获取构件处于服役状态下的残余应力。非破坏实验方法可以在确保构件完整性的前提下实现构件残余应力分布的计算,X-ray衍射法就是一种常用的非破坏测量方法。Marola等[9]基于X-ray测量了AlSi10Mg合金的残余应力分布。宋志飞等[10]利用X-ray衍射法对岩石试件进行不同入射角度的掠入射衍射测量,得到岩石中不同方向矿物晶体的衍射峰位变化,再依据布拉格定律得到测量点的应变,通过弹性材料应力-应变关系得到测点的残余应力。尽管该方法精准高效,但一般也仅用来测量少量点的残余应力。高昂的测试成本使得其难以独立且大规模地应用在构件残余应力分布场的测量中,因此发展一种高效且能获取整个构件表面的残余应力测量方法具有重要意义。
基于X-ray技术获得的少量离散实测值,可以通过插值法、有限元模拟法及反演方法获取构件表面余下部分的残余应力值。插值法是一种基于纯数学的计算方法,插值过程中不考虑构件自身所服从的力学约束,因此难以获得准确的计算结果[11]。有限元模拟法在建模的过程中需要对构件加工过程的热力耦合条件进行简化处理,极易产生较大误差。一个准确的残余应力分布场既要吻合对应实测点的应力值,也要满足弹性力学约束,结合实验测试与有限元模拟的反演方法有望成为解决该问题的重要途径。为了简化研究对象,许多学者常采用含有少量参数的基函数来描述残余应力在构件表面的分布情况。由于待反演参数较少,因此计算效率较高,但该方法易发生欠拟合,难以表征复杂的残余应力场。为此,现基于有限元模型修正法(finite element model updating,FEMU)发展一种无需构建基函数的残余应力反演方法,该方法无需考虑先验知识,只需对所有单元的未知参数反演即可。由于FEMU反演效率较低,为了进一步提高反演效率,结合深度学习技术,将人工神经网络技术作为有限元仿真软件的代理模型[12]。
人工神经网络技术是一种可以替代有限元程序进行实时计算的方法。神经网络通过调整神经元权重学习输入和输出参数之间的复杂映射关系,能够实时对输入和输出关系进行预测。事实上,由于神经网络具有优异的非线性拟合能力,很多研究工作都尝试使用神经网络替代有限元程序进行实时仿真[13-14]。Ali等[14]发展了一种有限元仿真耦合深度神经网络的技术,训练收敛的深度神经网络可以代替有限元仿真准确地预测纤维增强复合材料层合板渐进损伤本构规律。Park等[15]使用神经网络代替有限元计算,准确而高效地获得了泡沫铝的本构参数。从已有的研究中不难发现,神经网络不仅可以显著地提高反演效率,还具有与有限元仿真相近的预测精度。卷积神经网络是一种深度前馈神经网络,其由卷积层、池化层和全连接层组成。卷积神经网络具有良好的容错能力和泛化能力,非常适合高度非线性关系的预测。作为一种深度卷积网络,UNet[16]在解决力学非线性问题上展现出了巨大的应用潜力。Mendizabal等[17]将其应用于三维悬臂梁和心脏模型中,准确地建立了接触力与有限位移的非线性关系,证明了UNet在拓扑结构快速仿真方面的应用价值。Koeppe等[18]将UNet应用到有限元子模型技术中,精确地预测了与模型塑性历史相关的应力、节点力和位移。为了提高反演效率,现将采用 UNet 结构代替有限元模型修正法中的有限元计算对构件的残余应力场进行模拟。
结合上述研究,首先,通过有限元仿真技术生成大量温度场与残余应力场的映射数据;其次,基于深度卷积网络UNet建立温度场与残余应力场的映射关系;最后,将训练好的UNet代替传统FEMU中有限元修正的部分,对未知的残余应力场进行反演。以期通过数据驱动的方式建立残余应力预测模型,对实际工况下材料/结构残余应力分布的实时测量提供参考价值。
1 残余应力场
所涉及的研究内容主要有以下3个方面:基于有限元模拟生成训练UNet所需要的数据集;训练UNet神经网络;基于训练收敛的UNet代替ABAQUS反演残余应力场。
1.1 残余应力反演理论
参数反演本质是一个优化问题,旨在寻找一个服从某些约束前提下与实测值最小化差异的模拟结果。FEMU是常用的力学参数反演方法之一,现已广泛应用在材料参数识别中。由于残余应力分布的复杂性,采用传统的FEMU会消耗大量时间。为此,采用深度神经网络作为有限元仿真的代理模型对残余应力进行实时计算。
为了表征不同工艺条件、不同边界条件下构件的残余应力,选择合适的待反演参数至关重要。在热分析中,当已知热力学参数为单元中点温度和热膨胀系数时,有限元模型无需位移或力边界条件便可产生不同实验条件下的应力场,因此通过假定单元中点温度和热膨胀系数参数来获得残余应力,从而生成深度神经网络训练所需要的样本。为了尽可能丰富训练样本,提高模型的泛化性,在给定热膨胀系数的前提下于有限元单元的几何中点处施加随机温度,通过控制温度场来模拟产生残余应力场的不同工艺条件。因此,优化任务实质是寻找能够满足反演残余应力与目标残余应力差异最小化的温度场分布,即

(1)

图1所示为基于UNet的反演流程图。为了验证算法的有效性,实测的残余应力点由有限元仿真实验生成,采用优化算法更新每个有限元单元中点处的温度值使得目标函数最小化,采用的优化算法为拟牛顿法。

图1 反演技术流程图Fig.1 Flow chart of the inverse method
1.2 有限元模型
选用方形开孔铝合金构件进行研究,方形开孔模型作为复杂结构的简化可以很好地验证所提出的残余应力反演算法的有效性。图2为使用商业有限元软件ABAQUS建立的方形开孔试件的示意图,模型被划分为512个单元(CPS4R),弹性模量为70 GPa,泊松比为 0.3。在生成训练数据环节中,仅需在单元中心施加随机温度值,即可生成该温度下的残余应力场。输入的随机温度场作为神经网络的训练集,生成的残余应力场则为训练集所对应的标签。在验证模型有效性的环节中,在模型原有基础上设置Mises屈服应力为 200 MPa。为了获得模拟的残余应力场,模型中间施加了对称约束,上下加载端施加了80 MPa的外载使模型发生塑性变形,随后完全卸载掉模型上的载荷,把模型中仍存在的应力视作残余应力。

图2 方形开孔构件有限元网格示意图Fig.2 Finite element mesh diagram of square open-hole model
1.3 UNet网络结构
UNet[18]是一个成熟且经典的卷积神经网络结构,成功地应用在医学图像分割问题中。如图3所示,该网络是对称结构,包含一条收缩路径(左侧)和一条扩展路径(右侧)。收缩路径类似于一个自动编码器,能将输入空间转换为低维表示;而扩展路径类似于一个解码器,它可以将低维空间恢复到图像原始尺度大小。编码路径包含 4个下采样过程,每个下采样依次由两个3×3 卷积层和一个步长为2的2×2池化层组成。卷积层学习不同温度场的力学响应 (如应力场)。在每一个下采样步骤中,特征通道数量翻倍,特征图大小缩小为上一步输入特征图片的1/2。通道用于存储特征图,且每个通道存储一张特征图。网络的底部有两个3×3卷积层连接编码器和解码器。与编码路径类似,解码路径包含4个上采样过程,每一次上采样依次由一个2×2反卷积层和两个3×3卷积层组成。在解码时,来自同一状态的编码路径特征图需要裁剪并拼接到上采样特征图中,以完成信息的融合。在解码路径中,每经历一次解码,特征通道数减半,特征图的大小翻倍。最终通过一个3×3的卷积层把最后一张特征图转换到输出通道,即把应力分量分别存储在不同通道中。特征图的数量控制着网络的预测精度,理论说来特征图越多,则表征的问题越复杂。针对所研究的构件残余应力分布,通过比较不同数目的特征图预测效果发现,当特征图数目分别为128和256时,预测效果最好。

图3 UNet网络结构Fig.3 UNet architecture
1.4 数据生成及模型训练
充足的训练样本是模型具有高精度预测能力的核心,借助有限元软件生成方形开孔模型温度场映射残余应力场的数据样本。为了使得样本数据更具有普适性,采用拉丁立方采样法[19]对变量空间进行实验设计,最终确定采样的温度区间介于(-130,130) ℃。
这样通过在模型每个单元设置随机温度的方式,可以生成具有梯度的残余应力场,重复运行ABAQUS即可生成所需要的数据集,温度与残余应力均产生自网格单元的中心,整个模型共有512个单元,故得到的512个测点,共生成了5 800份训练样本。
由于标准的UNet输入图像为n×n×m格式的数字矩阵,其中n与m均为大于0的正整数。但由于采用的模型为方形开孔模型,无法满足模型的输入格式,因此在训练之前,对图像进行了预处理,通过立方插值将其转化为标准格式。
最终将有限元网格处理为16 × 16的数字矩阵。另外,考虑到有限元模型中心留有开孔,这部分参与计算会影响结果的准确度,所以在网络中增加了掩码(mask)处理方式,即将中心无数据区域进行标注,使其在网络梯度优化过程中不参与计算,如图4所示。
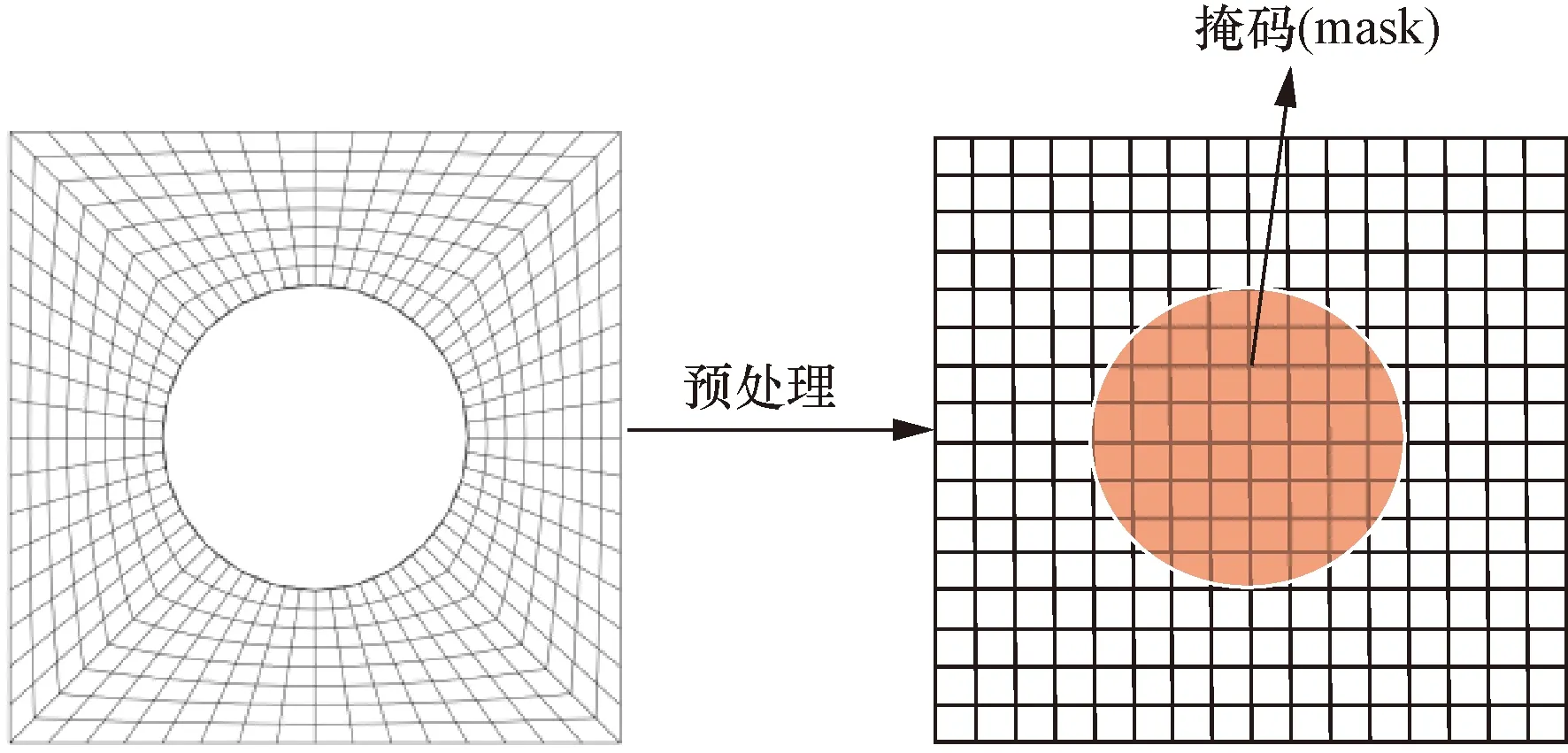
图4 数据预处理Fig.4 Data preprocessing
为了消除指标之间的量纲影响,采用式(2)对数据集做标准化处理,表达式为

(2)
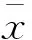
基于Keras库搭建UNet神经网络模型,网络采用均方误差(mean squared error,MSE)作为损失函数,Adam作为优化器,学习率设为10-5,激活函数为 ReLU,训练次数设置为1 000 次。
研究框架如图5所示。
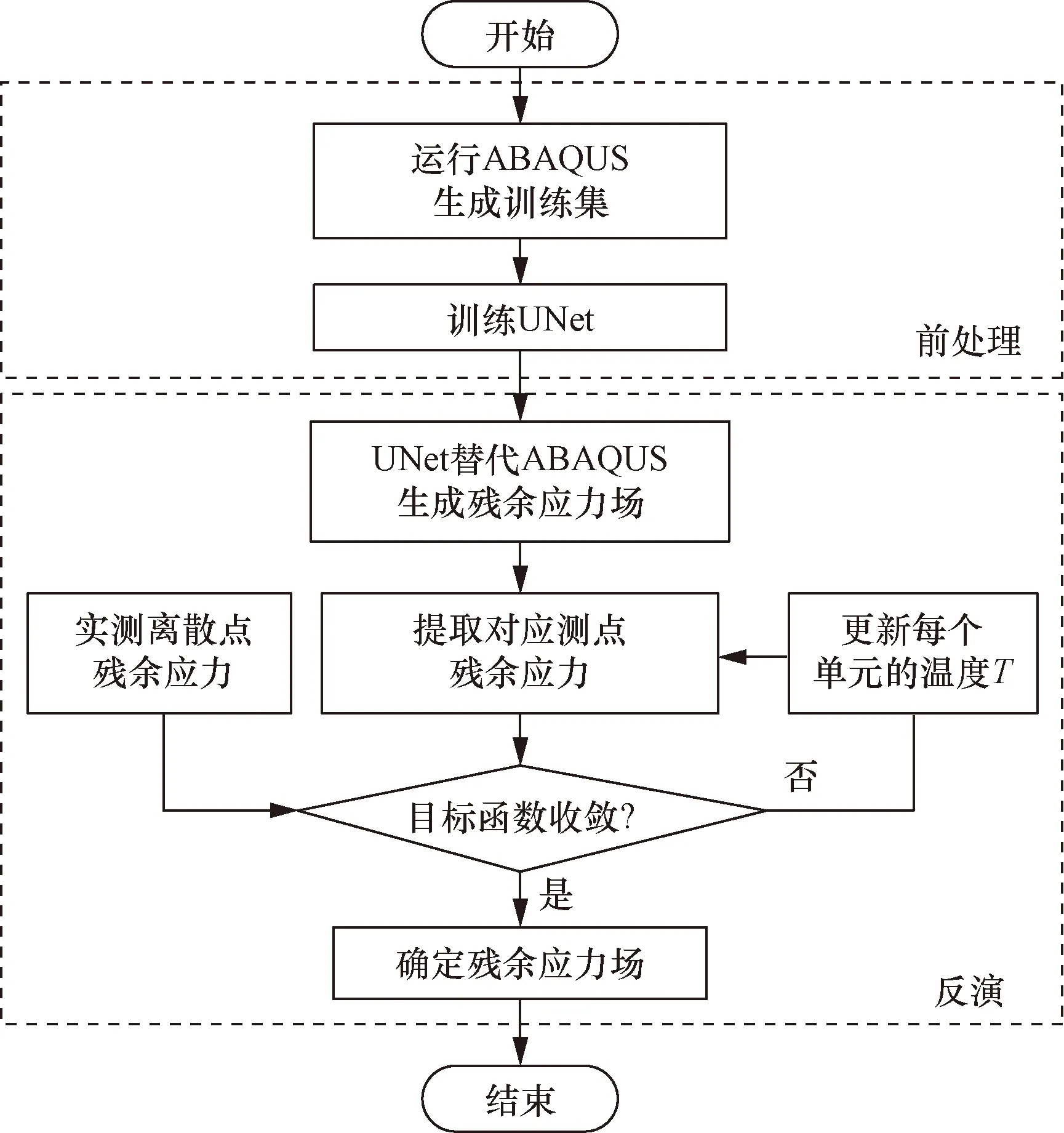
图5 残余应力反演计算流程图Fig.5 Flow chart of the inversion of residual stresses
2 计算结果
2.1 UNet模型验证
为了验证UNet结构在反演中的有效性,利用有限元模拟得到的残余应力场对其进行验证。
图6所示为采用了图2有限元模型及边界条件得到的有限元模拟残余应力场及反演得到的残余应力场。随机选择构件表面总点数的1/4作为反演所用的实测点。从图6中可以明显地看出,UNet预测结果与有限元模拟结果吻合度较好,在边界等敏感区域也有不错的表现,应力集中区域也预测得较为准确,充分地体现了UNet神经网络强大的映射能力。

图6 有限元仿真与UNet预测结果对比Fig.6 Finite element simulation versus UNet prediction
2.2 反演误差分析
为了更直观地展示UNet的预测结果,图7所示为不同实测点数目下应力分量σx的相对误差统计图。由于0 MPa附近的相对误差较大,并不能表征其实际的误差程度,因此此处仅给出了绝对值在10 MPa以上不同实测点与总点数比例下(1、1/2、1/3、1/4、1/5)的相对误差曲线,测点位置均为随机选出。由图7可见,随着测点数减少,计算得到的残余应力的误差越来越大,当使用全部测点进行反演时,超过20%误差的比例仅为1.89%,当仅使用1/5测点时,相对误差超过20%的单元占比已达16.80%。当选用1/4比例的测点时,可以看出其误差水平与1/3和1/2比例下相差无几,因此在对误差要求不是特别严格的前提下,1/4占比的实测单元是一个比较合适的比例。

图7 相对误差与不同测点比例关系曲线Fig.7 Relative error versus ratio of elements
2.3 反演效率对比
表1比较了利用UNet和FEMU在Intel i7,12 核,主频为3.2 GHz,内存为16 G配置的电脑上的反演效率。如表1所示,采用UNet方法在优化过程中迭代一次的时间为0.07 s,而FEMU优化迭代一次则需要20 s。基于UNet的反演方法在98次迭代后收敛,在包括采样时间和训练时间情况下,一个完整优化任务需要的时间约为39.35 h。由于FEMU反演太慢,在3 d内并没有实现FEMU的收敛,所以在此假设两种方法需要迭代相同的次数,在UNet方法中,最终大约经过了106迭代而收敛,在此迭代水平下,基于FEMU的反演方法估计需要花费5 555.56 h,其计算时间远远大于基于UNet的反演方法。由此可见,基于UNet的反演方法在计算效率上明显优于传统的有限元模型修正反演方法。
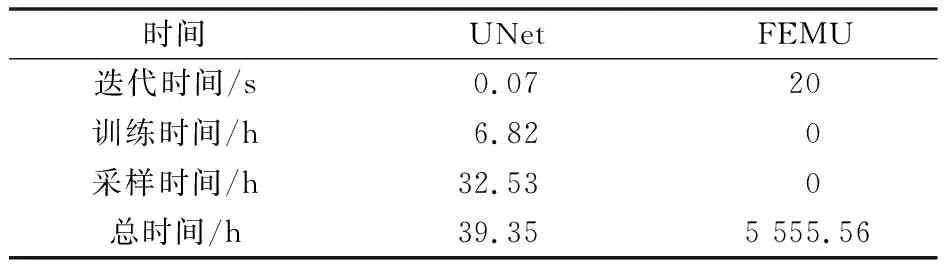
表1 UNet和FEMU优化时间对比Table 1 Comparison between UNet and FEMU in optimization time
3 结论
在考虑满足物理规律的前提下,从有限实测点高效预测全场残余应力是一个极具挑战的任务。发展了一种深度学习技术的残余应力反演方法,通过代替满足力学约束的有限元程序可以更高效地预测构件表面残余应力场。主要结论如下。
(1) 无需知道构件产生残余应力的工艺条件,基于神经网络的残余应力反演方法,通过有限测点便可获得满足力学规律的全场残余应力。
(2) 根据温度场与应力场数据训练的 UNet 神经网络在预测残余应力场时具有优越的性能,极大地提高了反演效率。
(3) 提出的使用卷积神经网络的反演方法不仅适用于残余应力的预测,也可用于其他力学参数的识别。
