基于拓扑优化的基座减振性能
2023-03-27孙启航张保成马翠贞邓子伟张凯
孙启航,张保成*,马翠贞,邓子伟,张凯
(1.中国海洋大学工程学院,青岛 266100; 2.青特集团有限公司,青岛 266100)
设备运转激励是激发海洋平台结构振动的主要来源之一,振动会对设备的运行稳定性和平台上工作人员的舒适性产生直接影响。基座作为动力设备和海洋平台之间的连接部件,是设备的振动激励载荷传递到平台结构的必由之路,开展基座优化设计是控制海洋平台结构振动的关键措施之一[1-2]。
近年来,国内外学者在隔振理论和技术研究方面开展了大量工作。Yang等[3]提出了两种新型的非线性阻尼减振系统,实现隔振性能的优化;Cremer等[4]提出了阻振质量的概念,为隔振提供了新思路,其研究表明将阻振质量或刚性结构安装在船体与基座连接处可以阻断振动波,从而减小振动的传递;Ding等[5]经分析对比发现,法兰盘式基座能将激励均匀地施加到艇体结构,减振效果相对于普通基座有了大幅度提升;Qi等[6]研究了推力轴承底座的输入阻抗对耦合声辐射的影响,提出了一种新型的具有高输入阻抗的推力轴承垂直对称底座。上述研究通过提出新结构或是增添新构件达到增大阻抗的目的,从而能够有效地抑制振动传递。
改变基座的各部分结构尺寸参数[7]、敷贴阻尼材料[8-9]、采用复合材料[10-11]、铺设阻振质量[12-13]都能够改变其阻抗,从而实现对振动响应的抑制;杨德庆等[14]、王语嫣等[15]提出了结构动力学优化方法,能够同时对刚度、阻振质量、阻尼等参数进行优化;夏志等[16]采用代理模型替代有限元模型,对比分析了4种常用代理模型的拟合精度;韩华伟等[17]研究了基座安装方式对减振效果的影响,特别指出当基座腹板对中基础结构肋板时,基座结构阻抗有所提高;叶珍霞[18]通过优化基座结构变量的方法,提高了基座一阶模态频率,从而达到减振的目的;秦浩星等[19-20]将蜂窝结构、声子晶体理论应用到基座结构设计当中,通过优化声子晶体的固有频率,使基座具有较好的低频减振性能和承载能力;刘学哲等[21]通过结构优化破碎机主轴及外壳来避开其共振频率范围,达到了较好的减振效果。上述方法大多都改变了基座原有的结构形式,在保持基座原有形式的基础上进行改进的案例非常少。
现以海洋平台设备常用典型钢结构基座为研究对象,采用结构拓扑优化设计方法,探讨不同的拓扑优化方案对设备基座振动传递特性的影响,为针对基座优化设计的海洋平台振动控制提供参考。
1 平台设备常用典型基座
1.1 基座形式
海洋平台上常用的典型设备安装基座结构形式如图1所示,主要由基座面板、腹板、肘板、双层底上下面板及两板之间的纵骨、横骨组成。
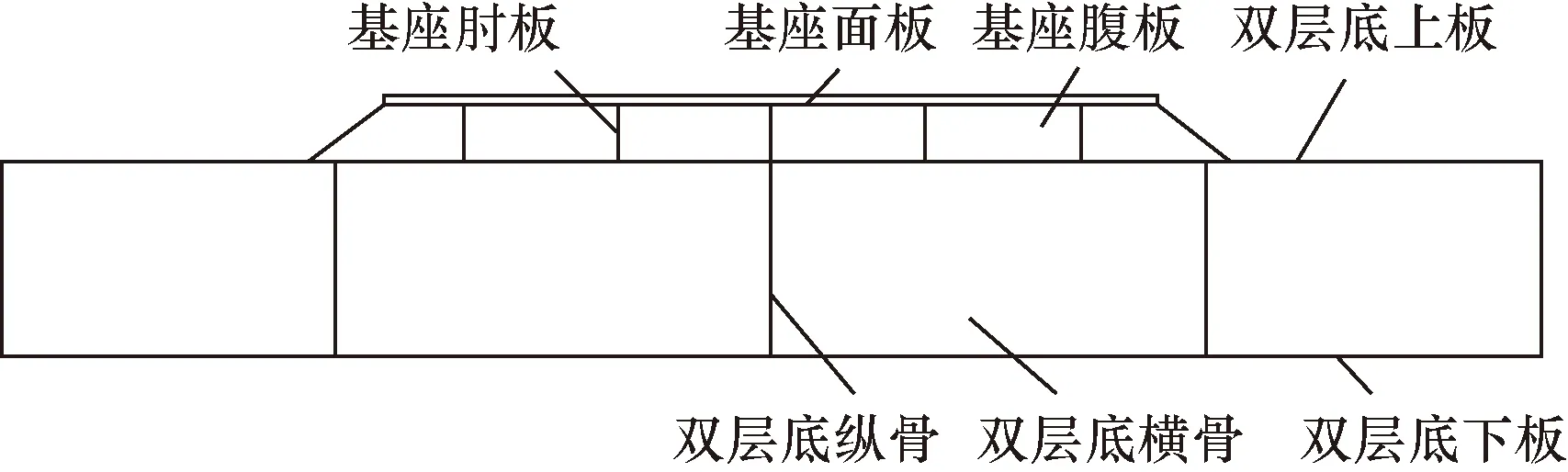
图1 典型基座结构Fig.1 Typical pedestal structure
某型平台设备基座的主要参数如下。总体尺寸为长2 400 mm,宽1 600 mm,高420 mm。基座面板长、宽、厚度分别为1 200、100、12 mm;肘板长、宽、厚度分别为1 500、100、6 mm;腹板上、下边长分别为60 mm和110 mm,厚度为6 mm;双层底的上板、下板厚度均为6 mm;横骨长、宽、厚度分别为1 600、320、6 mm,间距为700 mm;纵骨长、宽、厚度分别为2 400、320、6 mm,纵骨间距为500 mm。材料参数为:弹性模量E=210 000 MPa;泊松比σ=0.3;密度ρ=7 850 kg/m3。
建立上述平台设备基座的有限元模型,如图2所示。基座结构均采用壳单元模拟,对双层底的下板采用固定约束。

图2 某基座有限元模型Fig.2 Finite element model of the certain pedestal
1.2 基座减振评价指标
工程振动问题常采用分贝值度量,某点振动响应的加速度级为
(1)
式(1)中:ak为该点加速度,m/s2;a0为基准加速度,a0=1×10-6m/s2。
当评价点数量为n时,评价点群的加速度级为
(2)
式(2)中:Lk为第k个点的加速度级,dB。
加速度振级落差为
(3)
以基座面板上的所有节点作为输入端,标记为评价点群A;以双层底基座的下底板沿边缘处上的所有节点作为输出端,标记为评价点群B。
输入端评价点群A的均方根加速度表示为
(4)
式(4)中:M为输入端节点总数;aAi为输入端第i个节点的加速度,m/s2。
输出端评价点群B的均方根加速度表示为
(5)
式(5)中:N为输出端节点总数;aBj为输出端第j个节点的加速度,m/s2。
1.3 初始基座减振性能分析
在设备重心处施加垂向单位力,计算频率范围取10~400 Hz,计算步长为10 Hz,对基座进行扫频响应计算,得到其输入端和输出端的均方根加速度值,如图3所示,加速度振级落差如图4所示。由图3、图4可见,初始基座在激励频率为190 Hz时输入端评价点群的加速度幅值最大,其值为110.8 mm/s2,输出端评价点群的加速度幅值最大为73.6 mm/s2,其加速度振级落差为3.6 dB。

图3 评价点群的均方根加速度曲线Fig.3 RMS acceleration curves of the evaluation points

图4 加速度振级落差曲线Fig.4 Acceleration vibration level difference curve
2 基座拓扑优化方案设计
拓扑优化是一种根据给定的负载情况、约束条件和性能指标,在给定的区域内对材料分布进行优化的数学方法。从工程上来说拓扑优化是在一个设定的区域(设计区域)内,满足一定的边界条件(外载荷、特征频率等)的情况下,对材料进行重新分布,使设计获得预期的性能的优化设计方法。
运用Optistruct13.0软件作为优化设计工具,对各方案的优化结果进行比较分析。
2.1 基座拓扑开孔优化方案
以基座结构的肘板、腹板和双层底的纵骨、横骨中各单元密度为优化设计变量,输出端评价点群的加速度响应幅值最小为目标函数,基座结构的体积分数为约束函数。同时为确保基座结构动应力要满足强度要求,对输入端、输出端评价点群的加速度响应幅值进行限制,设置输入端、输出端评价点群的加速度响应幅值小于初始基座下的输入端、输出端评价点群的加速度响应幅值。通过拓扑优化获得满足约束条件的拓扑结构。
经过拓扑优化后基座结构的拓扑开孔密度云图如图5所示,选择拓扑变量值大于0.35以上的单元进行输出得到如图6所示的单元密度云图,根据图6确定基座的开孔位置和形状。
由于图6得到的结果仅是一种方案设计结果,不能直接应用于工程结构,因此对其进行重构,同时考虑到进行双层板的纵横骨开孔时开孔大小和位置需满足其承载要求,最终得到如图7所示的拓扑开孔的基座结构。
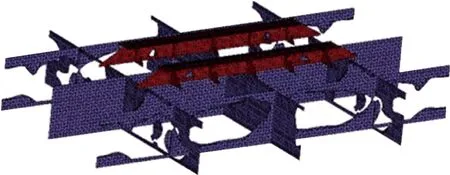
图6 拓扑变量值大于0.35的单元云图(基座拓扑开孔)Fig.6 Unit cloud diagram with topological variable value greater than 0.35 (pedestal topological opening)
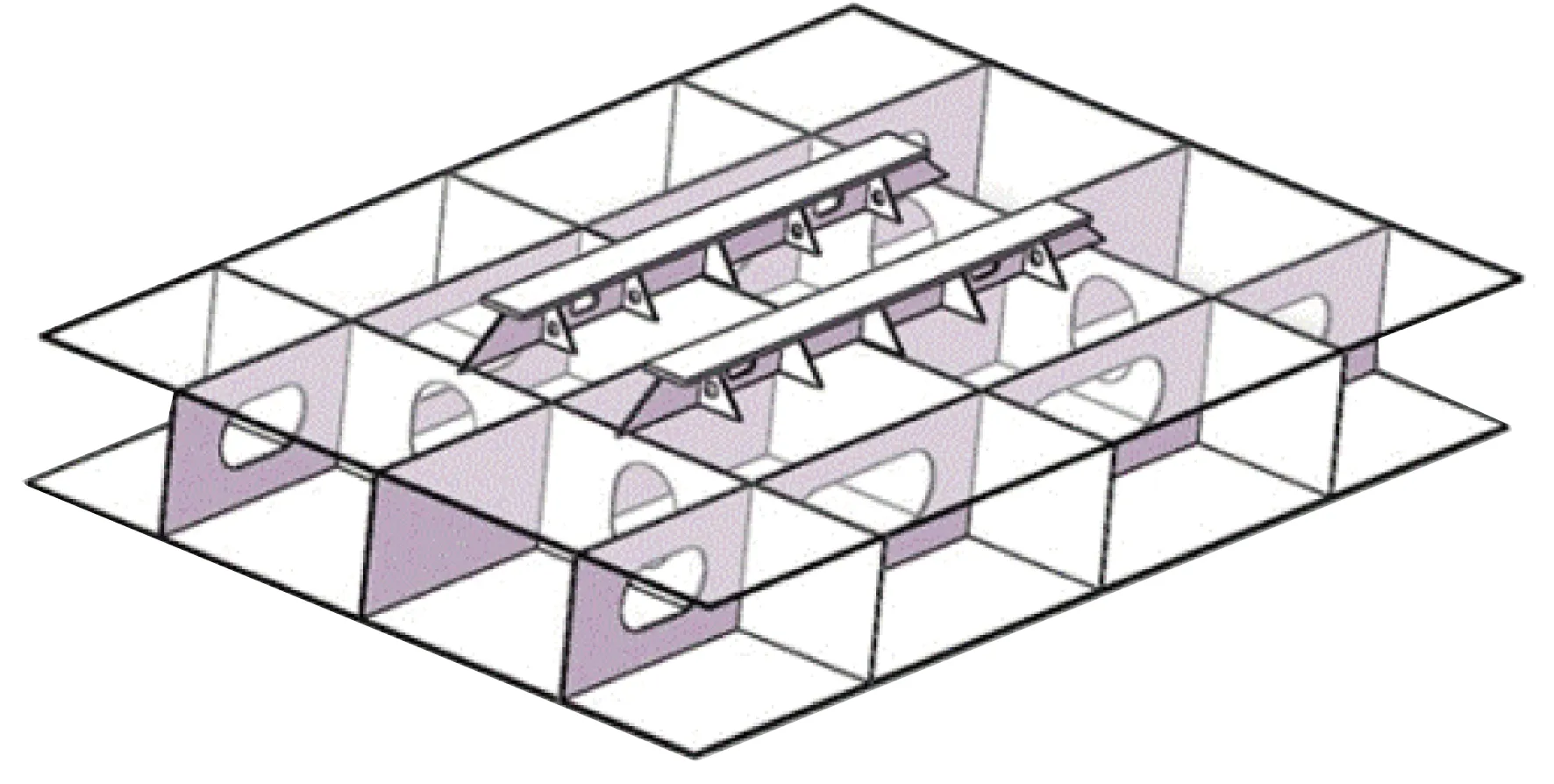
图7 拓扑开孔优化后的基座结构Fig.7 Pedestal structure of topological optimized by opening
对优化得到的基座结构进行频响计算,得到输入端、输出端评价点群的均方根加速度曲线,如图8所示。由图8所见,该优化结构的输入端评价点群的均方根加速度幅值最大为99.3 mm/s2,与初始基座相比有了较大的下降。优化后的基座输入端整体响应降低,但是在130 Hz处响应较初始基座有所提升,原因是开孔导致基座刚度降低。

图8 输入端评价点群的均方根加速度曲线Fig.8 RMS acceleration curves of the evaluation points at the input end
输出端评价点群的频响曲线如图9所示。由图9可见,输出端同样在130 Hz处响应偏大,除此之外的其他频段的响应都有所下降且响应幅值下降明显。优化设计前后基座的加速度振级落差如图10所示。可见在全频段范围内,优化设计结构优于初始基座。
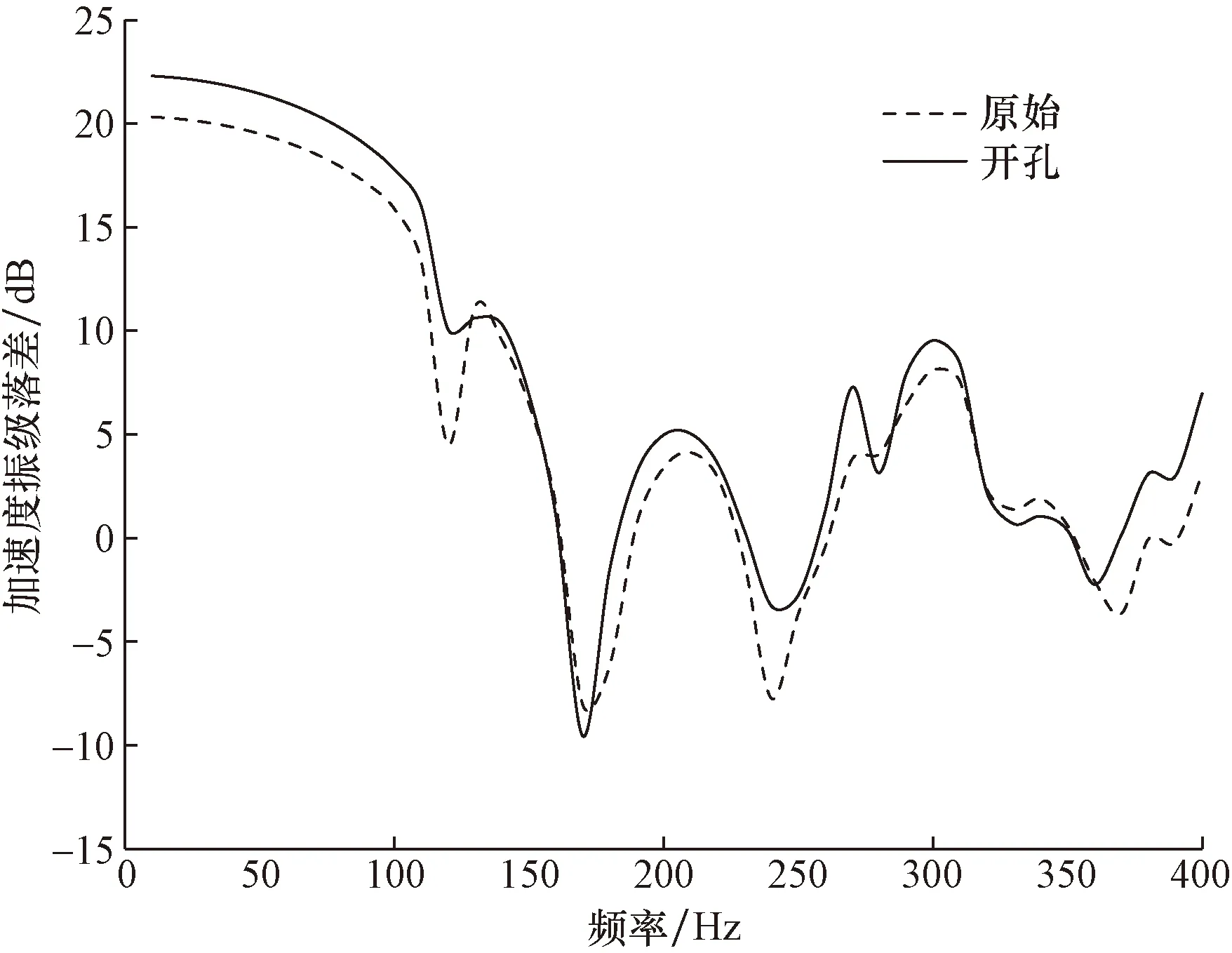
图10 加速度振级落差曲线Fig.10 Acceleration vibration level difference curves
2.2 基座拓扑加筋优化方案
虽然开孔优化设计结构的加速度振级落差有所提高,但改善不大。采取加筋板策略对初始基座进行再次优化,其中设计变量、目标函数和约束条件与开孔拓扑优化方案相同,不同之处在于本方案中需预设加强筋的起筋高度,设置最大起筋高度不超过板厚的5倍。经过拓扑优化后的拓扑加筋单元密度云图如图11所示。依据得到的优化结果,结合实际设置加强筋需满足的要求,设计出如图12所示的拓扑加筋基座结构。

图11 单元拓扑密度云图(基座加筋)Fig.11 Topology element density contour(pedestal reinforced)
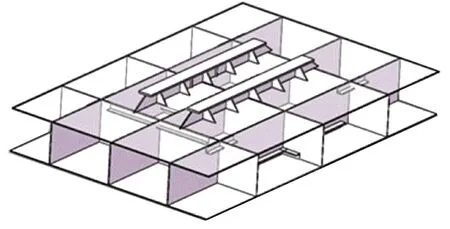
图12 拓扑开孔优化后的基座结构Fig.12 Pedestal structure of topological optimized by reinforcing
对优化得到的基座结构进行频响计算,得到输入端、输出端加速度曲线,分别如图13、图14所示。可见,基座进行拓扑加筋优化后,由于加筋增大了基座刚度,输入端加速度曲线峰值右移,最大幅值为88.9 mm/s2,较初始基座和开孔优化基座都有所下降。输出端加速度曲线与输入端相仿,也为峰值右移且峰值降低,下降幅度较大,但在330 Hz处有所回弹,整体减振效果较好。

图13 输入端评价点群的均方根加速度曲线Fig.13 RMS acceleration curves of the evaluation points at the input end
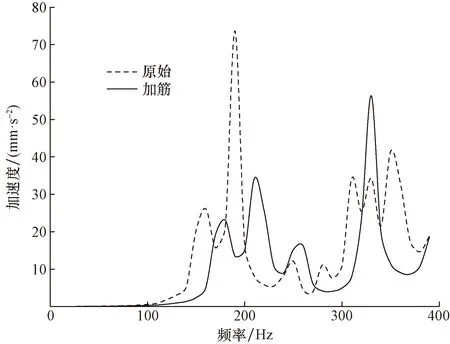
图14 输出端评价点群的均方根加速度曲线Fig.14 RMS acceleration curves of the evaluation points at the output end
如图15所示,加筋优化后的基座加速度振级落差在个别范围内小于初始基座,在大部分频段内都高于初始基座,减振效果较好。

图15 加速度振级落差曲线Fig.15 Acceleration vibration level difference curves
2.3 基座拓扑开孔与加筋综合优化方案
通过以上两种优化方案的分析可知,以上两种优化方案都可以达到减小振动响应的目的。但对基座结构开孔会使结构的强度有所降低,相比于拓扑开孔优化方案,拓扑加筋优化方案虽不会使结构的强度降低,但是设置加强筋会使基座结构的整体质量增加。综合以上两种方案,在拓扑加筋优化方案的基础上进行拓扑开孔,在保证结构刚度、强度的前提下,通过拓扑加筋与拓扑开孔的综合优化,减小振动响应,同时控制基座的重量。经过拓扑加筋与拓扑开孔综合优化后的结构单元密度云图如图16所示,选择拓扑变量值大于0.42以上的单元进行输出得到如图17所示的单元密度云图。
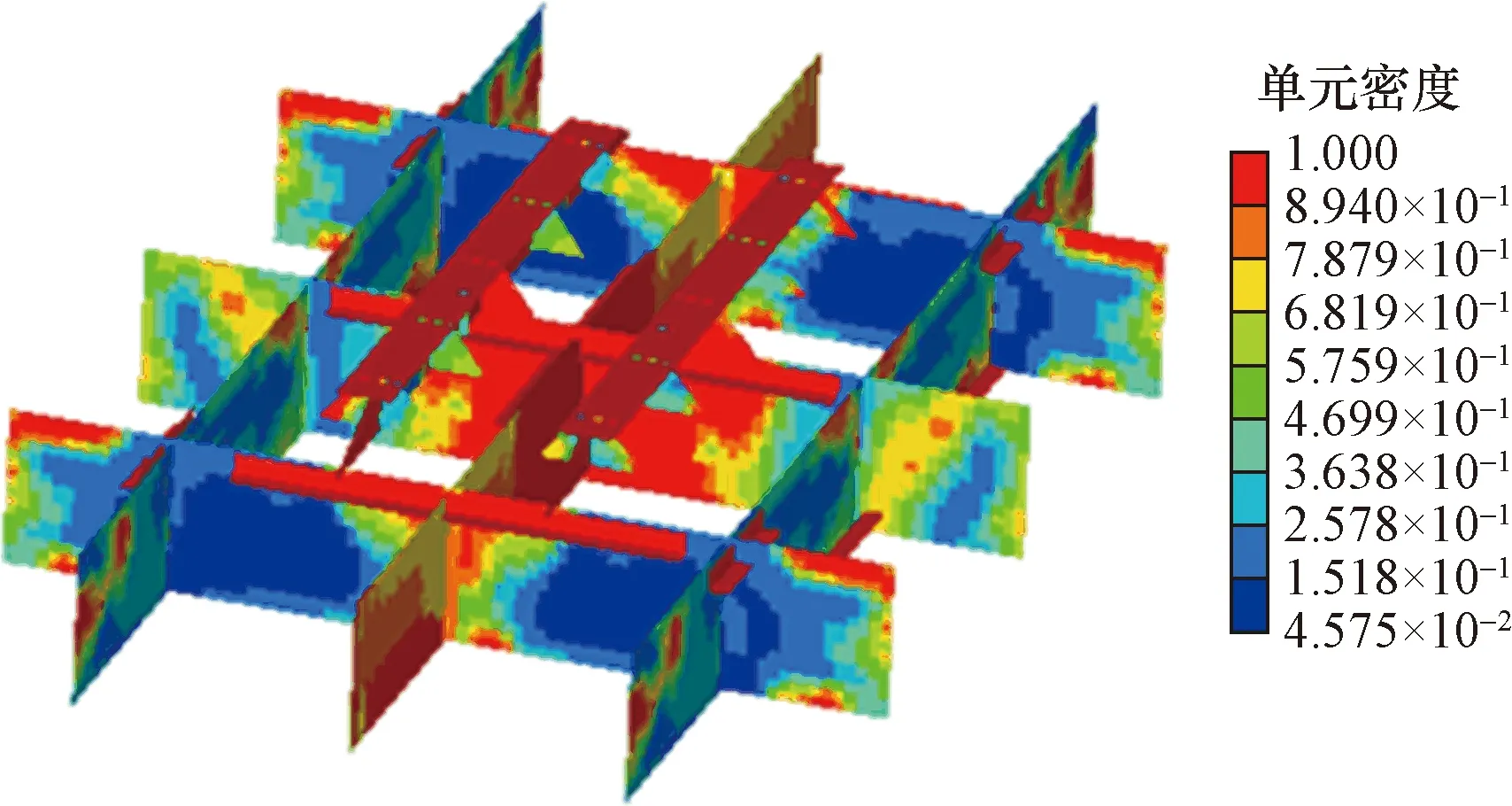
图16 单元拓扑密度云图(基座开孔加筋)Fig.16 Topology element density contour(pedestal opening and reinforced)
依据图17所示的单元密度云图,进行基座结构重构,结果如图18所示。对其进行频响计算,输入端、输出端加速度曲线分别如图19、图20所示。

图17 拓扑变量值大于0.42的单元云图(基座加筋开孔)Fig.17 Unit cloud diagram with topological variable value greater than 0.42(pedestal opening and reinforced)

图18 拓扑开孔与加筋综合优化后的基座结构Fig.18 Pedestal structure of topological optimized by reinforcing and opening
由图19、图20可见,拓扑加筋与开孔综合优化后的基座,输入端加速度峰值左移,第一处峰值响应变大但最大峰值大幅度降低,幅值最大为83.1 mm/s2。输出端加速度曲线峰值左移,且峰值较之前均有不同程度的减小,减振效果良好。
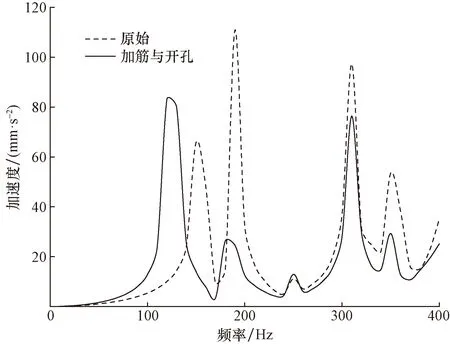
图19 输入端评价点群的均方根加速度曲线Fig.19 RMS acceleration curves of the evaluation points at the input end
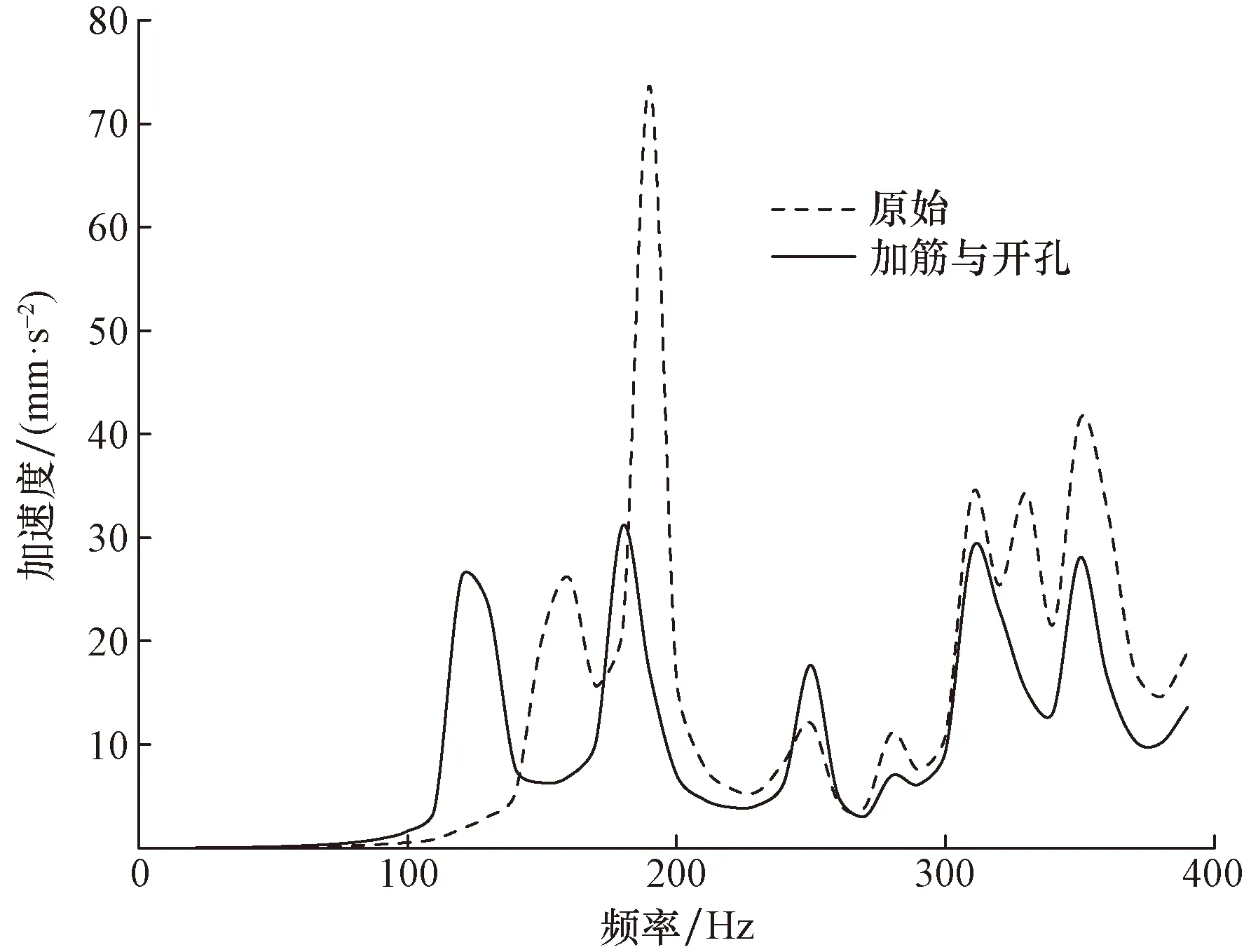
图20 输出端评价点群的均方根加速度曲线Fig.20 RMS acceleration curves of the evaluation points at the output end
如图21所示,拓扑加筋与开孔综合优化后的基座,其加速度振级落差与初始基座相比,振级落差较大,说明综合优化后的基座减振效果良好。

图21 加速度振级落差曲线Fig.21 Acceleration vibration level difference curves
2.4 基座优化方案对比分析
4种基座输入端频响曲线对比情况如图22所示。由图22可见,优化后基座由于刚度质量变化,其频响曲线峰值会偏移。开孔优化基座和加筋开孔综合优化基座第一处峰值提前且增大,说明在低频时基座面板的振动响应较大,在第二处峰值也就是最大峰值处,加筋开孔综合优化基座响应幅值大幅度降低。
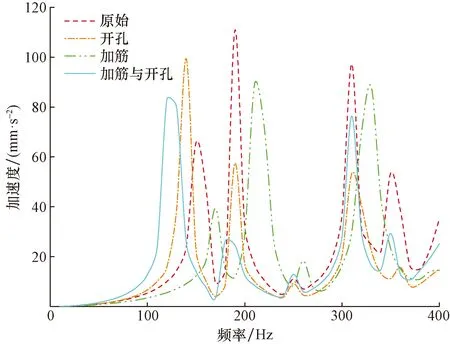
图22 不同优化方案下输入端评价点群的均方根加速度曲线Fig.22 RMS acceleration curves of the evaluation points at the output end under different optimization schemes
4种基座的输出端频响曲线,如图23所示。与输入端曲线类似,优化后基座频响曲线的峰值会向两侧偏移,与输入端对比,开孔优化和加筋开孔综合优化的第一处峰值下降很多,说明基座减振效果良好,而综合优化的基座在最大峰值处较初始基座下降的更多,减振效果最好。综合来看,加筋与开孔综合优化后的基座表现最好。4种基座的加速度振级落差,如图24所示。其中加筋与开孔综合优化基座的振级落差最大,因此加筋与开孔综合优化设计为最优设计方案。
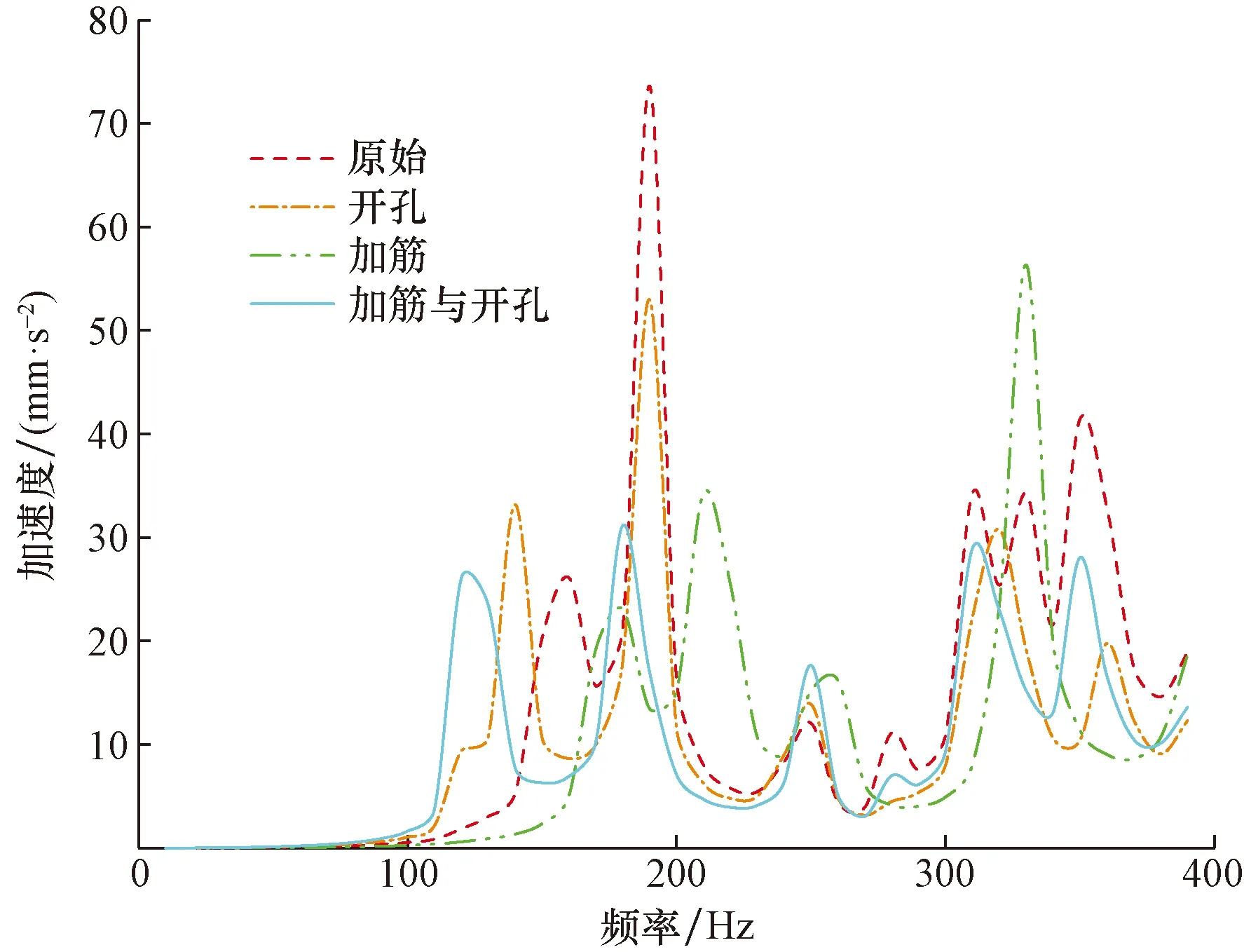
图23 不同优化方案下输出端评价点群的均方根加速度曲线Fig.23 RMS acceleration curves of the evaluation points at the output end under different optimization schemes
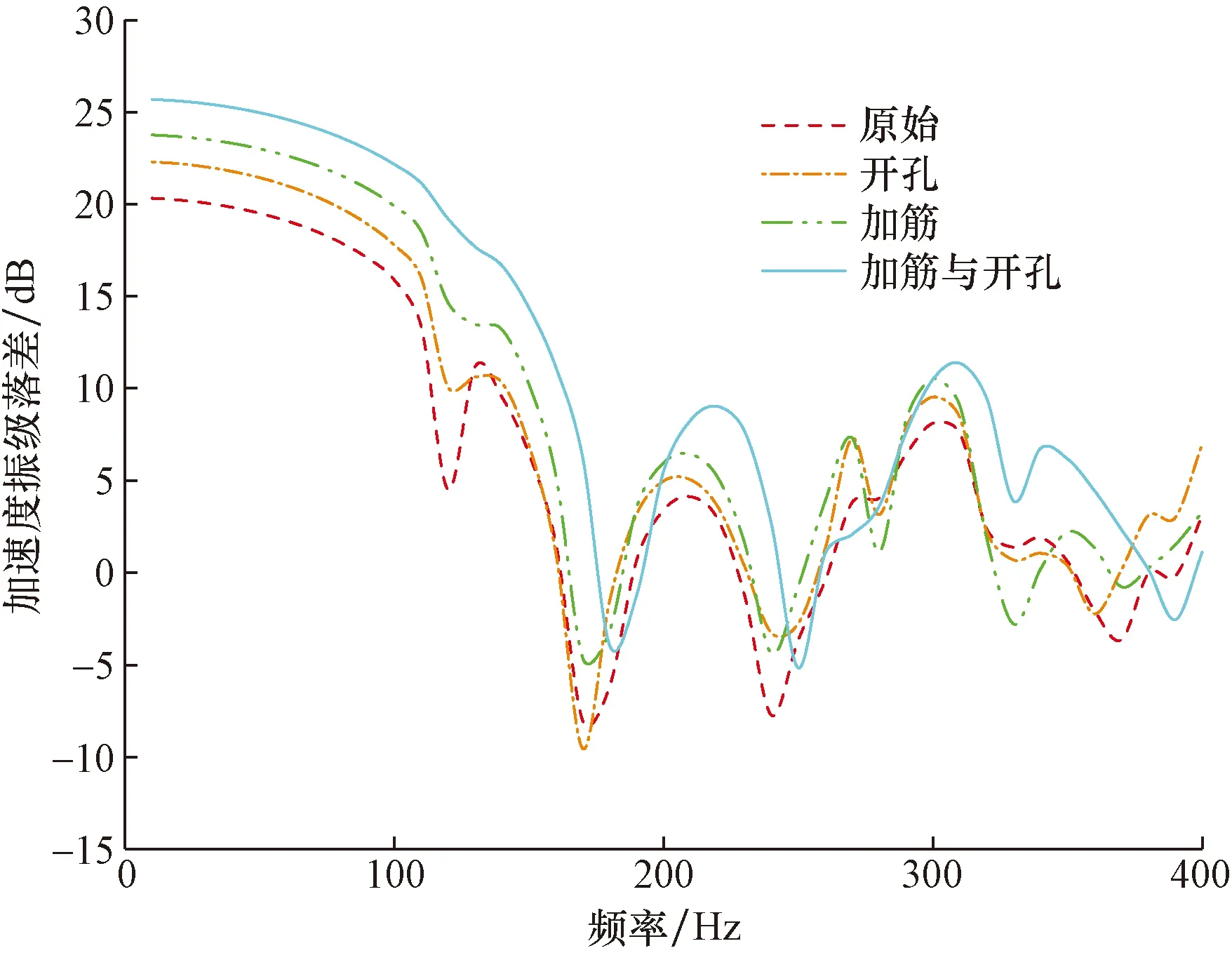
图24 不同优化方案下的加速度振级落差曲线Fig.24 Acceleration vibration level difference curves under different optimization schemes
对3种方案下的新型基座的重量进行计算,初始基座质量为584.8 kg,拓扑开孔优化方案下基座的质量最小为555.5 kg,拓扑加筋优化方案下基座的质量最大为612.5 kg,拓扑加筋与开孔综合优化方案下基座质量为576.1 kg,较初始基座质量稍有减小。
3 结论
以海洋平台常用典型钢制基座为研究对象,采用拓扑优化方法对其进行优化设计,总结出3种优化方案,分析对比3种优化方案,可得到以下结论。
(1)基座结构的变化导致质量刚度发生变化,使得频响曲线的峰值在频率轴上偏移。
(2) 3种优化方案下基座的减振性能较初始基座都有所提高。其中,拓扑加筋与开孔综合优化后的基座减振效果最好,加速度响应最大幅值处所对应的振级落差由3.6 dB提升至12.3 dB,且基座的总质量也略有降低,达到了预期通过拓扑优化设计提升设备基座减振性能的目的。
