稀疏码分多址技术发展及前景
2023-03-27雷拓峰倪淑燕崔亮程乃平宋鑫陈世淼
雷拓峰,倪淑燕,崔亮,程乃平,宋鑫,陈世淼
(1.航天工程大学研究生院,北京 101416; 2.航天工程大学电子与光学工程系,北京 101416; 3.66407部队,北京 100144)
随着第五代移动通信技术(5th generation mobile communication technology,5G)在全世界迅速发展,科研学者逐渐将研究重点转向第六代移动通信(6G),以引领通讯领域实现巨大飞跃。目前,5G物联网技术仍主要依托于4G中长期演进技术(long term evolution,LTE)的物理层解决方案[1],并且主要使用正交多址技术(orthogonal multiple access,OMA),在6G物联网中,垂直行业的各种业务将需要支持大量的设备连接,因此提升系统的频谱效率是6G中一项关键的研究技术[1]。其中,非正交多址技术(non-orthogonal multiple access,NOMA)的出现有效解决了大规模物联网通信(massive machine type communication, mMTC)中频谱利用率的问题,并且NOMA也可以减小各用户之间的相互干扰[2],降低系统过载[3],已被认为是一种非常有前景的解决方案。目前非正交多址技术主要有3种方案:功率域非正交多址(power-domain non-orthogonal multiple access,PD-NOMA),码域非正交多址(code-domain non-orthogonal multiple access,CD-NOMA)以及其他非正交多址方案。作为一种码域的非正交多址方案,稀疏码分多址技术(sparse code multiple access,SCMA)是在低密度签名技术(low density signature,LDS)的基础上发展的。然而,与LDS不同的是,SCMA将不同资源上的比特信息映射为多维码字,提升了系统的映射分集,因此,SCMA具有更优秀的误码率性能[4-7]。此外,相比其他NOMA方案,SCMA结合了频率分集与调制技术,具备强鲁棒性以及高可靠性等特点[2-3]。
关于SCMA的研究主要集中在3个方面: SCMA的码本设计[8-10]、SCMA的解码算法[11-13]以及SCMA技术的应用[14-16]。其中,SCMA的码本设计主要决定SCMA的误码率性能[2],同时也间接影响着接收端解码算法的迭代次数。解码算法的研究主要集中于降低接收机端解码的复杂度上[12-13],同时兼顾SCMA的误码率性能。此外,由于SCMA优秀的兼容性,其可以与很多技术结合从而进一步提升系统性能,如与信道编码[17-18]、多天线[19]以及调制等技术结合[20]。
截至目前,国内外相关学者在该研究领域取得长足的进步。如英国埃塞克斯大学的Noor-A-Rahim等[21]与萨里大学的Wen等[22]在SCMA关键技术的研究中处于领先地位,并取得了较多的研究成果。此外,印度理工学院的Deka等[20]聚焦于SCMA与正交时频空调制的相关研究。并且国内关于SCMA的研究也发展迅猛,如台湾大学Chen等[2]带领的团队致力于SCMA码本的设计,电子科技大学李成林[23]以及北京邮电大学鲁坤[24]关于SCMA开展的理论以及相关技术的验证,以及重庆邮电大学等多所院校也都相应开展了关于SCMA的研究[25-26],并呈现出海量的研究成果。因此,现聚焦于SCMA现阶段的研究成果,对SCMA技术的发展进行梳理,进而为SCMA在未来通信中的研究提供参考。首先,在SCMA码本设计层面,简述SCMA编码原理,系统梳理现有码本设计方案,分析对比其优缺点,并给出一些新的研究思路;其次,在SCMA解码算法层面,分析两种基本解码算法的解码机理,对比其特点和解码复杂度,并结合当前的一些改进算法和新兴算法探讨解码算法潜在的改进思路;再次,在SCMA与其他技术结合方面,系统总结SCMA与MIMO、信道编码技术结合的研究成果,分析其技术难点,并探讨SCMA与新兴通信技术的结合;最后,分析目前SCMA技术仍旧存在的问题以及需要解决的关键技术,并对SCMA相应技术的发展进行展望。
1 SCMA码本设计
近几年关于SCMA码本设计的研究非常多[27-41],如Chen等[8]基于强化学习设计了上行高速率SCMA码本,Jiang等[33]基于最大平均互信息提出了一种码本设计方案,Zhang等[42]基于唯一可分解的星座群,提出了一种码本设计方案。然而,这些码本的设计方案可以总结为两种方式,第一种方式是基于信道容量进行设计分析,如文献[28,32-34];另一种方式则是根据误码率进行设计分析,如文献[14,35-36]。尽管两者采用的分析方式不同,但是最终得到的设计准则一致,均为最大化最小欧式距离(AWGN信道),最大化最小乘积距离(Rayleigh信道)。因此,可以采用任意一种方式对SCMA码本进行分析,并不会影响码本最终的设计准则。目前码本的设计可以总结为3个方面:传统的SCMA码本、高调制速率的码本以及高维度SCMA系统的设计。
1.1 传统的SCMA码本设计
以4频率6用户SCMA系统为例,其编码器的原理如图1所示,在SCMA系统中,每一个用户都有一个特定的码本,将比特信息映射在相应频率的码字上。对于上行用户而言,多用户的码字首先会经过信道乘性衰落,因此在基站接收到的信号是发送码字与衰落系数相乘的叠加码字,如图2(a)所示;对于下行信道而言,如图2(b)所示,多用户的码字首先会经过叠加处理,然后基站会将叠加的码字信息发送给多用户。因此,多用户接收到的信息是叠加码字与信道衰落系数的结果。SCMA码本设计是一个较为复杂的优化问题。为此,许多学者提出了相应的简化设计方案[2,33,36-40]。其中,采用旋转操作符将基准母码本变换到相应多用户码本的设计方案应用较为广泛。
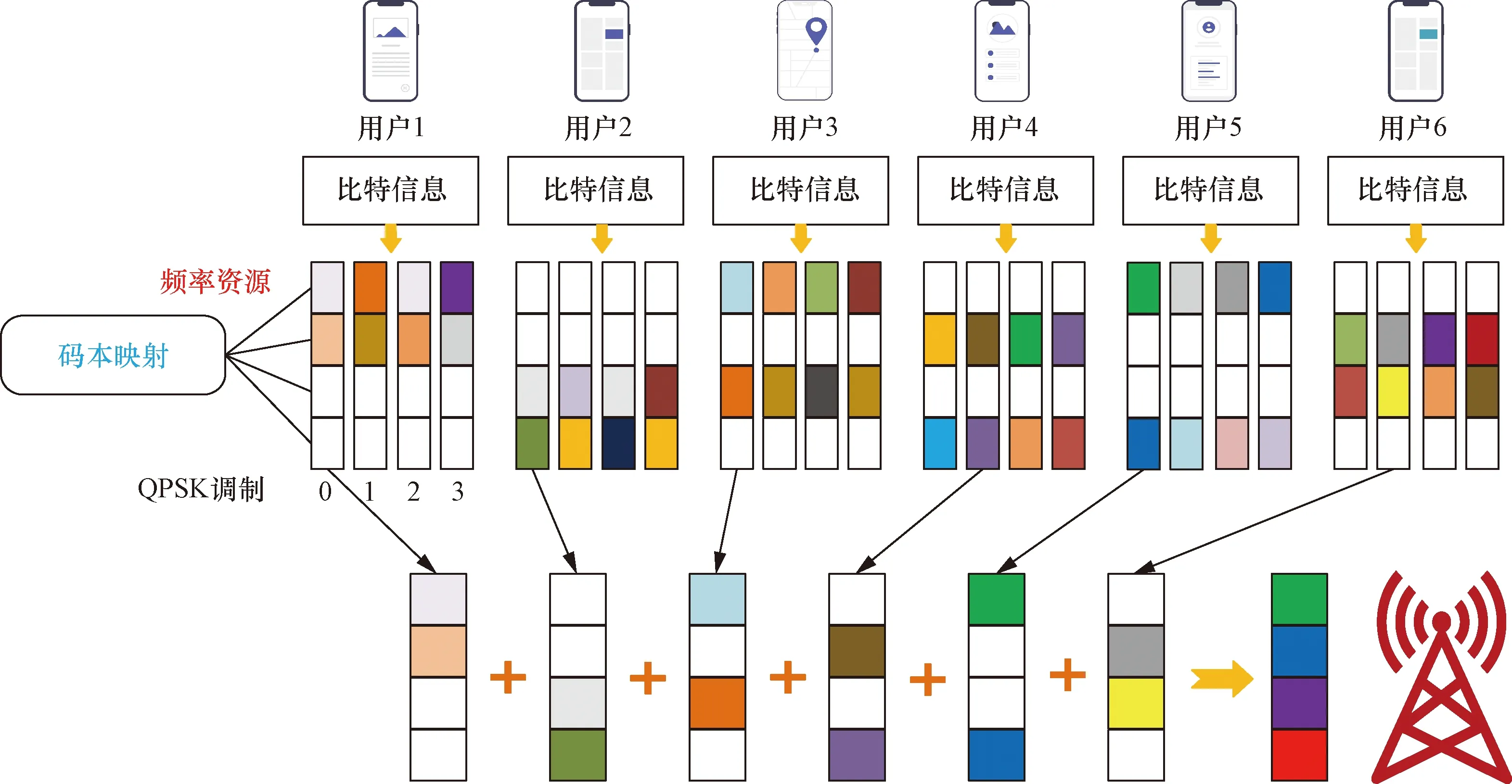
图1 SCMA编码原理图[40]Fig.1 The encoding diagram of SCMA[40]

h1、h2分别表示各用户的衰落系数;x1、x2表示各用户发射的码字图2 上行用户与下行用户的区别Fig.2 Differences between uplink users and downlink users
对于瑞利上行信道,多用户码本可以设置为与母码本一致[2]。因此,在上行信道中只要设计出最优的母码本即可,并不需要考虑旋转操作步骤。在上行信道中,现有主流的母码本设计方案是通过将基准星座点(如QPSK、QAM、GAM等调制方式)在不同频率下进行重新排列以获得高维的母码本。目前,已有许多研究给出了相应的算法以解决星座点排列的问题,如符号交换算法[2,4]、维度排列切换算法[28]、二进制交换算法[41]、交叉操作算法[10]以及强化学习算法[8]等。以上算法都是通过提升SCMA母码本的映射分集,来获得更好的误码率性能。假若母码本在不同频率下采用相同的映射符号进行传输,此时SCMA可以视为LDS传输系统。因此,LDS也可以看作是SCMA的一种特殊情况。然而,当调制速率或者码本维度过高时,采用上述一些算法会导致母码本设计的复杂度呈现指数式的增长,从而难以快速得到最终结果。因此,如何快速有效地获得母码本是一个亟待解决的难题。
而对于下行信道,由于用户接收的是多用户叠加码字,因此,需要同时考虑母码本设计以及最优的旋转度数。目前,在下行信道中有两种常用的设计方案:第一种方案是在上行信道的基础上,进一步采用旋转、映射等操作符将母码本转变为多用户码本[29,33]。该方案相对简单且易于实现,但寻找最优的角度仍然是一个比较困难的问题,Chen等[2]采用遍历的方法获得了最优的旋转角度,但是该方法相对复杂度较高,对于负载更多用户的系统,采用遍历搜索方法会导致搜索时间呈指数增长。此外,也可以采用启发式算法来搜索最优的旋转角度,但是结果表明,该方法仍然具有较高的复杂度[33]。因此,如何有效快速得到最优旋转角度也是该领域面临的一大挑战。另一种方案则以最大化最小欧式距离或者最大化最小乘积距离为准则,采用传统或启发式优化算法对SCMA码本进行优化[30]。该方案不需要旋转角度的辅助,可将码本设计视为一个约束优化问题,通过采用不同的优化方法以获得SCMA码本。例如,Wang等[30]将码本设计问题视为一种二次规划问题,并且采用CVX优化工具中的半定松弛方式解出了优化的码本。相对于第一种方案而言,该方案难以保证各用户误码率的公平性,因此,设计出的码本可能会由于多用户码本的不同而产生不同的误码率性能。
对于AWGN信道而言,其信道衰落系数可以视为恒值1。因此,AWGN下的码本设计可以视为瑞利下行信道的一种特殊情形,也可采用适用于瑞利下行信道的设计方法[40]。
1.2 高调制速率下的码本设计
在传统SCMA码本设计中,如何快速构建不同频率上星座点的编号是母码本设计的主要问题之一。目前,大多数研究工作仅考虑了调制速率在16阶调制及其以下的情况,其中所采用的码字设计算法如表1所示。例如,符号交换算法[2,4]、维度排列切换算法[28]等。可以看出,这些算法的设计思想均是改变不同频率上的码字的映射来获取符号分集所带来的增益。研究发现,母码本的设计问题也可以借鉴二次分配问题的求解方法。其中,Samra等[43]在研究多包传输问题时将符号映射视为二次分配问题(quadratic assignment problem,QAP),有效地提升了多包传输系统的误码率性能。因此,SCMA的母码本设计也可借鉴Samra等的研究思路,采用QAP方法以解决母码本的设计问题。

表1 母码本设计算法Table 1 The mother codebook design algorithms
二次分配问题是数学优化和运筹学分支中最基本的组合优化问题之一。为了解决工厂选址问题,Koopmans等[44]提出了二次分配优化。如图3所示,已知,需要在N个位置布置N个工厂,各工厂都需要其他工厂生产的原料,并且各工厂之间的运输成本均不相同。为了最小化运输成本,需要优化设计各工厂的位置从而降低总运输成本,其数学表达式可以写为
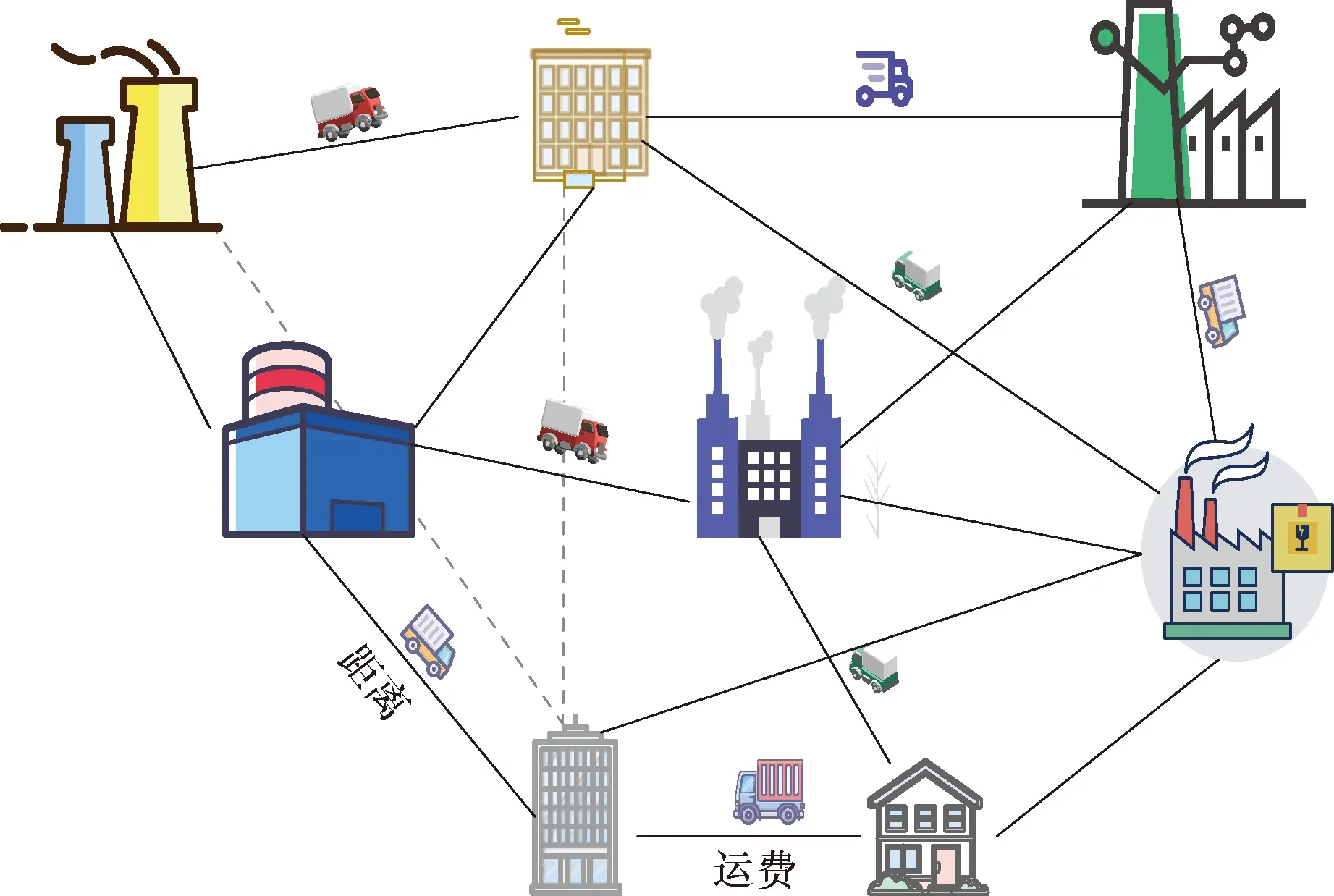
图3 二次分配问题示意图Fig.3 The diagram of the quadratic assignment problem
(1)
式(1)中:π:{1,2,…,N}→{1,2,…,N}为工厂的选址结果;ψ为所有可能的选址结果;fij为从第i个工厂到第j个工厂的单位运输费用;dπ(i)π(j)为第i个工厂到第j个工厂的距离。因此,可以将母码本的设计问题视为二次分配问题,进而可以有效解决母码本的设计问题。目前,可以采用多种算法解决QAP问题[45-53]。此外,Chen等[2]和Xiao等[28]提出的算法(码字交换算法,维度排列切换算法)可以总结为Tabu算法的一种特殊情况。码字交换算法与Tabu算法都是通过不断交换码字顺序来取得可能最优的排列结果,不同的是,Tabu算法还进一步采用禁忌表,并设置了相应的禁忌步长以避免落入局部最优的结果。因此,Tabu算法能够更加快速得到排列结果。
1.3 高维度SCMA系统的设计
为了支持未来大规模用户连接,SCMA系统将不再局限于传统的4频率6用户。因此,设计出高维度的SCMA系统显得尤为重要。表2给出了目前已有的高维度SCMA系统设计方案。然而,关于高维SCMA因子图矩阵的研究相对较少[3-4,34,54-55],尽管Vameghestahbanati等[3]给出了SCMA因子图矩阵的设计方法,即任意两个用户不能同时采用相同的频率进行传输,但是他们并没有给出设计的本质原因。但是,Li等[55]研究表明可以采用低密度奇偶校验码(low density parity check,LDPC)中校验矩阵的设计方法来构建因子图矩阵,然而他们设计的SCMA系统仍与传统系统的负载因子一样均为1.5。但是总体而言,该方法对高维度SCMA系统的设计具有启发式的作用。

表2 高维度因子图矩阵设计方案Table 2 The schemes of designing high dimensional factor graph matrix
在Li等[55]的研究基础上认为,类似于LDPC中的校验矩阵校验节点与变量节点的关系,SCMA因子图矩阵决定了用户与频率的承载关系,但是因子图矩阵的设计需要考虑解码算法对其的影响。消息传递算法(message passing algorithm, MPA)算法与LDPC中的置信传播算法(belief propagation,BP)类似,BP算法和MPA算法都是基于树图去求解各用户的边缘概率密度从而进行译码[56]。当因子图矩阵为树图的情况下,各用户均可得到准确的边缘概率密度信息,因此,SCMA系统的误码率性能最优。然而,SCMA的因子图矩阵存在不可避免的“环”现象,使得各节点的信息会在“环”中循环,从而导致各用户不能得到准确的边缘概率密度信息。为了减小“环”对SCMA性能的影响,在LDPC中常见的做法是通过构造校验矩阵去减少“环”的存在,尤其是短“环”现象。因此,SCMA因子图矩阵的设计也可以采用该种方式来减少短“环”的存在。目前,构造校验矩阵的方法主要有限几何构造法[57]、组合设计法[58]、渐进边生长构造[59]和比特填充构造法[60]等。
此外,更多用户的码本设计也是需要考虑的问题之一。对于频率节点度数更大的SCMA系统而言,由于同一频率负载的用户数目更多,叠加星座点的欧氏距离将会变得更小,从而导致SCMA系统的误码率性能急剧降低。并且频率节点度数的增大也会带来更大的设计复杂度,假设采用旋转操作来获取多用户码本,负载用户数量的增多将会导致搜索最优角度呈指数增长。此时,遍历搜索的方法将不再适用于高维度SCMA码本的设计。因此,需要探索复杂度更低的码本设计方法。
2 SCMA解码算法
在SCMA系统中,解码算法同样至关重要,解码算法的性能直接影响系统的误码率性能和解码复杂度[61]。目前,主流的解码算法可以分为消息传递算法、期望传递算法(expectation propagation,EP)以及一些新兴的解码算法。
2.1 消息传递解码算法

p(X,y)=p(X)p(y|X)
(2)
式(2)中:
(3)
式中:hk,l为第l个用户在第k个频率上的信道衰落系数;σ2为接收端的信噪比。那么,在因子图矩阵已知的情况下,可以采用消息传递来获得各节点的边缘概率密度,其中消息的更新规则[11,19]可以写为
(4)
(5)

近几年来有许多关于消息传递的改进算法研究,如log-MPA算法、Max-log-MPA算法、基于阈值的消息传递算法[13]、球形消息传递算法[62]以及基于压缩感知的MPA算法[63]等。上述这些改进的消息传递算法并没有改变消息传递的本质结构,从而其复杂度并不会大幅下降。
2.2 期望传递解码算法
高斯近似的消息传递算法是将离散的变量简化为连续的高斯近似函数,通过K-L散度得到高斯近似函数的均值与方差[16,64-65]。在消息传递的过程中,该算法仅传递各用户消息的均值与方差。高斯近似传递算法可以将解码算法的复杂度大幅降低,但是在计算均值函数时,仍会产生大量的计算复杂度[66]。在高斯近似传递算法的基础上,期望传递算法采用高斯函数近似均值。因此,相比于高斯近似传递算法,期望传递算法能够进一步降低解码端的复杂度。
在MPA算法中,各节点将离散的信息进行更新,如式(4)、式(5)所示,从而导致解码复杂度较高。而在期望传播算法中,各节点更新的是消息的均值μ与方差ξ[12],即
(6)
类似于改进的消息传递算法,期望传递算法也可以采用相应的改进手段进一步降低复杂度。如Max-log-EP解码算法[67-68]和基于QR分解的EP算法[69]。此外,当用户数目急剧增多时,将会导致更加复杂的因子图网络结构,而采用变分方式去简化因子图结构[16]也可以进一步降低期望传递算法的复杂度。此外,也可以进一步借鉴MPA已有的改进算法对EP算法进行改进,如基于阈值的EP算法和基于排序的EP算法等。
2.3 其他的解码算法
除了上述两种常见的解码算法之外,神经网络等算法也被用于SCMA解码端[70-76]。例如,基于深度学习的解码算法,Wei等[70]将SCMA的解码器视为一个多输出的分类问题,每一个输出预测相应用户发送的符号;基于球形的SCMA解码算法,Vameghestahbanati等[77]通过限定搜索空间来降低复杂度;基于蒙特卡洛马尔科夫链的解码算法[78],其复杂度呈线性增加;基于概率密度离散化的FFT方法可以加快信息更新速率提升解码性能[11];此外,类似于期望传递算法,Yuan等[79]采用Bethe函数近似各用户的消息传递,使得算法的复杂度也呈线性增长。
由于SCMA与多输入多输出系统(multiple-input multiple-output,MIMO)结构类似,因此也可以将MIMO中相应的算法应用到SCMA系统中,如高斯树近似算法[16],高斯树近似-串行干扰消除算法[80]以及基于Beth函数近似的消息检测算法[81]。在MIMO系统中,Wu等[66]采用高斯近似的一阶信息进一步将算法的复杂度降低为O(M+df)。而在现有的SCMA解码系统中,EP解码算法仅能将算法的复杂度降低为线性增长为O(Mdf)。因此,在SCMA系统中也可以借鉴MIMO中的解码算法,去进一步降低解码端算法的复杂度。
3 SCMA与其他技术的结合
SCMA具备良好的兼容性,因此也可以与很多技术进行联合设计,如MIMO、OFDM等技术。
3.1 SCMA与MIMO技术的结合
目前,SCMA与MIMO技术结合较为广泛,分别为MIMO-SCMA的空时编码以及低复杂度的解码算法。在MIMO-SCMA空时编码中,Pan等[82]首次将Alamouti码和准正交STBC扩展到多维空间,但是仅考虑了下行信道下的空时编码方案。对于上行信道而言,Li等[83]研究了上行信道下空时编码的设计准则并分析了其误码率性能,然而,SCMA的码本的调制阶数较低。相比于上行信道而言,下行信道下多天线发送的是多用户的叠加码字,因此下行信道下MIMO-SCMA空时码字的设计较为简单。而目前关于上行信道MIMO-SCMA空时编码的研究较少,主要是由于上行信道下各用户SCMA的空时码字设计相对复杂。因此,上行信道下MIMO-SCMA空时编码也是未来的一大研究热点。低复杂度的解码算法是MIMO-SCMA的另一个研究热点。为了进一步降低复杂度,普遍采用以期望传递算法为基准的改进算法。如基于QR分解降低了EP传递算法[69]、基于BP和EP的混合解码算法[84]以及基于比特层面改进的高斯近似传递算法[19]。
3.2 SCMA与信道编码技术的结合
通过将SCMA技术与信道编码技术结合,可以进一步提升系统的误码率性能。LDPC、Turbo、Rateless和Polar等SCMA编码系统的研究均集中在接收端。例如,Pan等[85]采用联合译码(joint iterative detection and decoding, JIDD)方案对Polar编码的SCMA系统进行解码;Sun等[86]在LDPC-SCMA中采用最小均方误差并行解码算法,并且采用40 nm工艺,制作了相应的芯片;此外,也有一些其他的译码算法,如边缘消除辅助迭代检测的译码算法[17]和混合检测译码算法[87]。可以看出,信道编码与SCMA结合系统的研究热点主要集中在解码算法上。然而,在现有的研究中,信道编码和SCMA编码仍被视为相对独立的两部分,是否可以将这两种技术进一步结合从而进行联合编码,目前还尚不确定。
3.3 SCMA与新兴技术的结合
此外,SCMA也可以和其他技术很好地结合。例如,Zeng等[88]提出的全双工通信方案FD-SCMA,可以满足未来物联网技术中海量用户接入的需求;Deka等[20]基于正交时频空(orthogonal time frequency space,OTFS)结构提出OTFS-SCMA的设计方案,可以克服高速运动物体多普勒对SCMA系统的影响,因而有望应用于未来卫星物联网通信;此外,SCMA还可以与光通信[89]和智能反射面等技术相结合[90],以进一步提升系统的性能。
随着5G的发展,万物互联、全息投影、太空和深海探索已成为人们不断追求的目标,但是5G技术也凸显出相应的局限性[91],而6G有望在未来数十年内解决这些问题。目前6G相关的技术,如人工智能、太赫兹通信、量子通信、无人机通信、全息波束形成、后向散射通信以及三维网络通信[92-93]等,已经成为学术界和业界的热门研究主题。并且SCMA已经成功应用于相应的技术中,如神经网络解码算法[73-74]以及强化学习的码本设计算法[8],SCMA技术在后向散射通信[94]以及航空自组网[95]中的应用等。得益于SCMA技术良好的兼容性,因而SCMA有望进一步与新兴的技术进行结合,以推动其在6G领域中的潜在价值。
4 总结与展望
作为一种新兴的多址技术,SCMA能够有效地解决5G中大规模机器以及物联网通信中频谱资源短缺的问题[96-98]。目前,SCMA技术的发展主要处于理论探索阶段,仍然存在诸多问题需要解决。为进一步挖掘SCMA技术在未来移动通信中的应用潜力,归纳总结了近几年来国内外关于SCMA开展的研究工作,并对SCMA技术潜在的发展挑战与趋势进行如下总结。
(1)高维度SCMA系统的设计。尽管给出了高维度SCMA因子图矩阵的设计方法,但是在高维度下,随着SCMA用户数量的增多,叠加星座点的欧式距离势必会导致误码率性能的下降,从而对SCMA整个系统造成严重影响。此外,随着系统维度的增加,消息传递算法无法满足未来移动通信低延时的需求。因此,如何在高维度下进一步提升系统性能以及探索具有更低复杂度的解码算法也是未来研究的主要方向。
(2)非规则的SCMA系统设计。目前,多数研究局限于规则的SCMA结构,即每一个频率上服务的用户数目相同,每一个用户采用的频率数目相同。然而,由于未来移动通信用户的需求各不相同,因此SCMA系统也需要针对各用户的通信需求进行设计,所以非规则SCMA系统的研究在该领域极为重要。目前已有的工作仅对非规则SCMA系统的性能进行了仿真分析,而缺乏对其结构的深入研究[99-102]。有理由认为,非规则SCMA系统的主要特点在于其因子图矩阵。因此,在非规则SCMA系统中,应注重因子图矩阵下各用户性能的研究,而非SCMA系统的性能。
(3)多径效应下SCMA系统的设计。由于各用户所处的地理位置不同,信号可能不会同时到达基站,从而会导致SCMA各用户同步错误[103]。尽管采用OFDM循环前缀可以消除同步误差,但是面向大量用户接入时,需要设置更长的循环前缀,这在现实场景中往往是不可行的[97]。此外,由于多径效应的影响,在不同时间各用户会有多路信号到达接收基站,从而会导致SCMA系统产生严重的符号间干扰。因此,如何避免SCMA系统中同步错误带来的问题仍有待解决。
(4)随机接入情况下SCMA系统的设计。随着通信用户数目的增多,SCMA系统也在朝着随机接入的情况下发展。各用户无法一直保持通信的状态,导致用户数目会随着时间的变化而变化。因此,需要考虑SCMA系统中用户数目的变化,在不改变已有用户码本的情况下,实时对SCMA系统的结构进行调整以适用于随机用户接入的情况。此外,低轨卫星覆盖面积大,相比之下各用户可能处于不同的波束内,或处于同波束不同的地理环境下。此时,各用户地理位置不同,造成通信链路的信道模型和接收端信噪比等信息的不同,并且用户的随机接入与资源的切换也更加复杂。因此,SCMA码本资源的分配也是未来尚需考虑的问题。
(5)不同信道下SCMA码本的设计。目前,多数SCMA的码本设计局限于AWGN信道和瑞利信道,显然这些研究并不能满足日益复杂度的信道环境。现有的信道模型有Suzuki信道、Loo信道、莱斯信道、遮挡的莱斯信道型等。因此,面向6G,需要设计适用于不同信道模型的SCMA系统。
(6)高速移动下SCMA系统的设计。在高速运动模型中,SCMA系统不可避免会产生较大的多普勒频移,在窄带信号中,多普勒频移带来的相移会影响接收信号的同步。同时,考虑到高速移动情况下,基站终端对用户的服务时间非常有限。因此,如何在有限的时间内满足用户通信需求,也是一个尚需解决的问题。然而,目前OTFS技术在多普勒频移较大的情况下仍然展示出较好的性能[20],因此,OTFS-SCMA有望应用于未来高速移动通信模型。
