顶浪中首固定翼波浪推进艇的运动响应和航速预测

2023-03-25张仕华王冬姣

舰船科学技术 2023年4期

张仕华，王冬姣，刘鲲

(华南理工大学土木与交通学院，广东广州 510640)

0 引言

近年来，随着海洋产业的发展，摇荡翼推进成为研究热点，许多优秀的水下和水面航行器被研发出来。波浪推进艇就是其中之一，将水翼安装在无人艇的首部或尾部，在波浪作用下水翼随艇体作摇荡运动而产生推力，以实现在海上长距离的航行。本文对安装了首固定翼的波浪推进艇进行相关研究。

水翼可通过振荡从周围的水流中提取能量[1]，Isshiki[2-3]提出波浪推进系统的概念，从理论和实验方面研究了来流速度、水翼截面、展弦比等参数对水翼推进性能的影响。De Silva 等[4]基于CFD 软件研究了垂荡与纵摇运动之间的相位差、傅汝德数以及波幅等参数对主动摇荡水翼船推进性能的影响。Belibassakis 等[5]通过在船首安装固定水翼，发现水翼不仅可以产生推力，还可以降低垂荡和纵摇的运动响应。Bøckmann 等[6]通过在船体上安装固定水翼，研究了波浪入射方向、水翼纵向位置对推力的影响。祝美霞等[7]采用三维面元法对水翼辅助推进船在规则波中的运动和增阻响应进行了预报，还对水翼展弦比和安装位置对船舶在波浪中的运动和增阻响应的影响进行了分析。封培元等[8]基于势流理论建立了顶浪海况下摇荡水翼与船体的频域耦合水动力模型，研究了水翼位置、浸没深度等参数对水翼推进性能以及船舶耐波性的影响。霍萍[9]在双体船模型上安装固定翼后进行了静水阻力模型试验及波浪中的自由航行试验。李冬琴等[10]基于重叠网格方法对不同波长下新型摇荡水翼的推进性能展开研究。胡峰等[11]利用平面运动模块研究了被动纵摇水翼在不同周期、波高等参数下的推进性能。邓超等[12]通过用户自定义函数（UDF）模拟了水翼的随船运动，以及自身的被动转动，分析不同振幅、周期和扭簧恢复刚度对推进性能的影响。

目前，对摇荡翼推进性能的分析大都是给定水翼运动，然后给定来流速度模拟水翼在流场中的受力和流场分布。对波浪推进艇而言，由于水翼和艇体之间距离较近，水翼与艇体之间存在复杂的水动力相互作用，波浪推进艇的航行速度未知且不恒定。本文通过DFBI 模块建立了含首固定翼之波浪推进艇的数学模型，允许其在纵荡、垂荡和纵摇3 个方向下自由运动，对波浪推进艇在顶浪条件下的自由航行运动进行数值模拟，得出艇体的运动响应、航行速度以及水翼推进性能，为波浪推进艇设计提供一定参考。

1 船体运动

在波浪作用下，艇体受到波浪作用产生六自由度运动，安装在船首的水翼跟随艇体作摇荡运动。

图1 展示了3 个坐标系，其中OXYZ为固定坐标系，原点O位于静水面，Z 轴垂直向上；第2 个为以船速U随船一起运动的坐标系oxyz，初始时刻（静浮时）o点位于静水面上，z轴通过重心垂直向上；第3 个坐标系Gxbybzb为固定在船体上的坐标系，G点位于船体重心上，xb轴方向指向船首。

图1 船体坐标系Fig. 1 Coordinate system of wave-propelled boat

为简便起见，入射波浪使用线性波，假设波幅为ζa，固定坐标系下波面位移方程为：

式中：k为波数；ω为波浪的圆频率；β为波浪传播方向与X轴之间的夹角，顶浪条件下为180°。

波长λ和波浪周期T可表示为：

固定坐标系和移动坐标系之间变换关系为：

结合式（1）和式（4）可得

式中，ωe为遭遇频率。

规则波中艇体重心的运动响应可以表示为：

式中：ηj0为j自由度方向的运动幅值；εj为j个自由度方向的运动响应与入射波浪之间的相位角。

波浪中水翼产生随时间变化的X方向的力Fx(t)，一个周期内的平均值为：

其中，Te为遭遇周期。

2 数值计算方法

2.1 控制方程

流场中任何流体的流动都基于流体力学的基本控制方程，即质量守恒方程、动量方程和能量方程。在船舶与海洋工程相关的计算中，水通常被认为不可压缩，仅需考虑质量守恒和动量守恒。

STAR-CCM +中数值模拟计算中所采用的质量守恒方程可表示为：

动量守恒方程为：

式中：ρ为流体密度；v为流体质点的速度矢量； ⊗表示外积；fb为作用在连续体单位体积上的体积力合力；σ为应力张量。

2.2 VOF 模型

流体体积法(VOF)是一个简单的多相流模型，它用于在混合物各相之间交界面的网格上模拟几种不相混溶流体的流动。相的分布和界面的位置用相体积分数αi来描述。第i相的体积分数定义为：

式中：Vi为网格单元中第i相流的体积；V为网格单元的体积。一个网格单元中所有相的体积分数总和必须为1：

根据体积分数的值，可以区分网格单元中不同相或流体是否存在：αi=0，表示网格单元完全没有i相；αi=1，表示网格单元完全由i相填充；0<αi<1，表示存在相间交界面。本文定义αi=0.5 为自由液面。

2.3 运动方程

物体质心位置平移运动方程根据全局惯性坐标系给出：

式中：m表示物体质量；f为作用在物体上的合力；U为物体质心处的速度矢量。

物体的旋转运动方程是在以物体的质心为原点的局部坐标系中给出：

式中：M为物体的惯性矩张量；Ω为物体的角速度矢量；N为作用于物体的合力矩。作用于物体上的力和力矩是由作用于物体每个边界的流体压力和剪切力得到的。根据计算得到的流场和压力场得到物体的运动。为了避免不必要的计算，可对物体运动进行约束。

3 计算模型及仿真过程

3.1 模型参数

计算对象波浪推进艇由水翼和双体船组成，表1为双体船模型的主要参数，图2 为安装了首固定翼的波浪推进艇模型。水翼转轴到水翼前缘的距离为0.25 个弦长，水翼转轴到船体重心水平距离为1.28 m。水翼采用NACA0018 翼型，假设水翼是零浮力且质地均匀的，弦长c取0.18 m，展长b取1 m，浸深为0.3 m。

表1 双体船模型参数Tab. 1 Parameter of the catamaran model

图2 波浪推进艇模型Fig. 2 Geometry of the wave-propelled boat model

3.2 数值模型

使用流体体积(VOF) 多相流模型模拟自由表面，选用雷诺平均纳维-斯托克斯方程(RANS) 和SSTkω湍流模型，采用二阶逆风方案对RANS 方程中的对流项进行离散，并采用Simple 方法求解分离流模型。使用动态流体相互作用(DFBI)模块结合重叠网格方法模拟双体波浪推进艇在波浪中的运动，允许模型在纵荡、垂荡和纵摇3 个方向下自由运动。

3.3 计算域和网格划分

如图3 所示，建立一个长方体计算域来模拟水翼和双体波浪推进艇周围的流体。模型相对于中纵剖面对称，为减少计算网格，在顶浪规则波条件下只取右舷进行数值模拟。Inlet，Top，Bottom，side 边界设置为速度入口，Outlet 边界设置为压力出口，Symmetry边界设置为对称平面、船体和水翼表面设置为无滑移壁面。图3 共有3 个区域，分别为背景区域、重叠区域和水翼区域，背景区域和重叠区域间建立重叠网格界面，在水翼区域和重叠区域间建立滑移网格界面，以实现区域之间质量、动量等模拟量的传递。

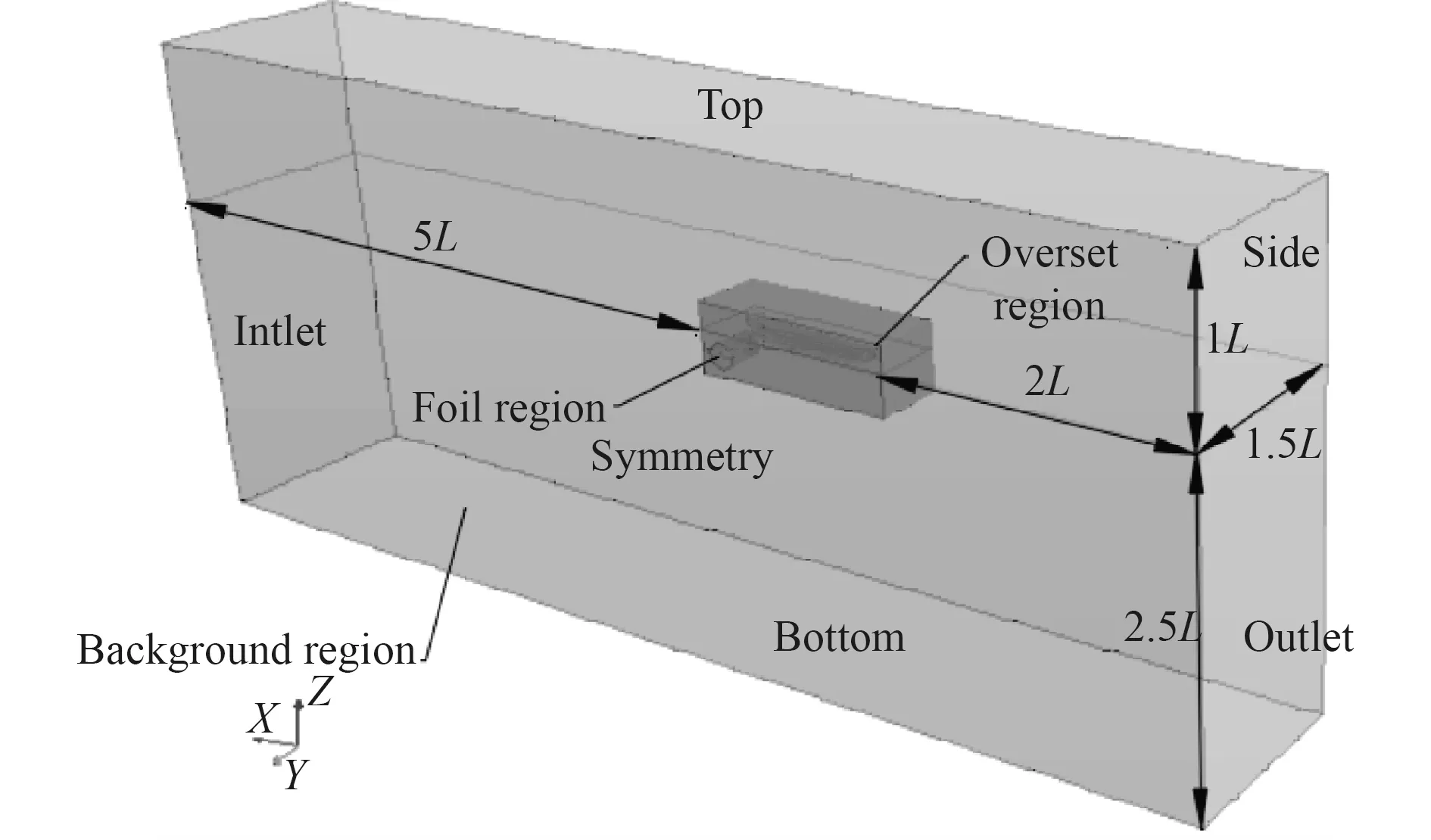
图3 计算域示意图Fig. 3 Schematic diagram of calculation domain

网格生成采用切割体网格，在船体表面和水翼表面应用棱柱层来捕捉湍流边界层，自由液面附近的网格进行局部加密，如图4 所示。

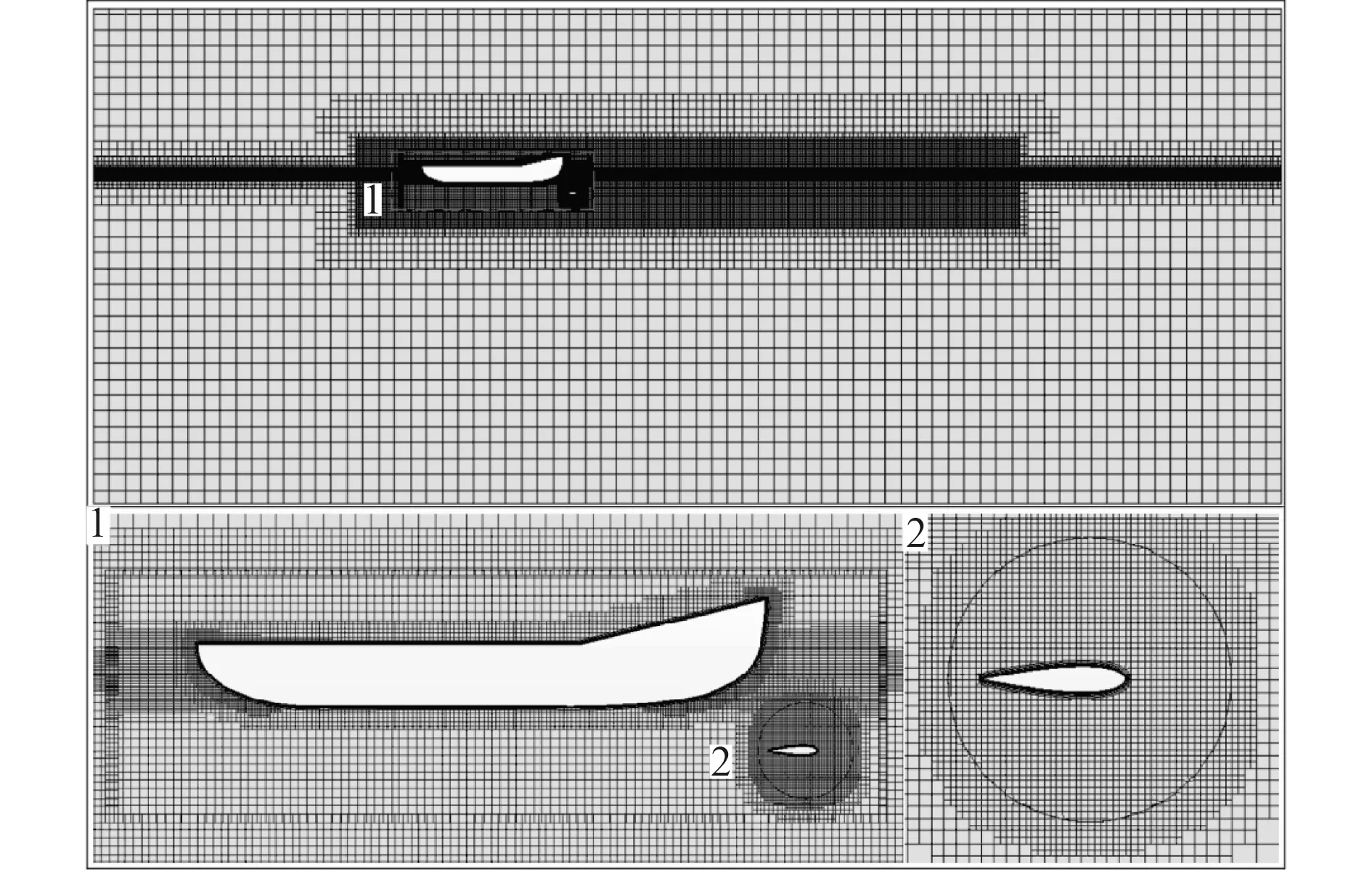
图4 网格划分示意图Fig. 4 Schematic diagram of mesh division

3.4 网格无关性分析

利用 CFD 方法进行研究时，一般要开展网格无关性分析，以评价不同尺寸网格对计算结果的影响。设计4 套网格进行网格无关性检验，保持背景域网格参数不变，重叠区域和水翼区域中相对基础尺寸百分比不变，仅调整网格的基础尺寸。

计算4 种网格尺寸下波浪推进艇0 航速状态下的纵摇运动响应。波浪周期取1.4 s，波高取10 cm，此时波长船长比λ/LWL约为1.5，船体纵摇运动幅度较大，大幅度运动往往会导致较大的数值误差。时间步长取T/256，T为波浪的周期。表2 为4 种网格尺寸下船体纵摇运动RAO 及相对误差，可观察到3 号网格开始计算值趋于稳定。考虑计算精度和计算效率，接下来的计算均采用3 号网格。

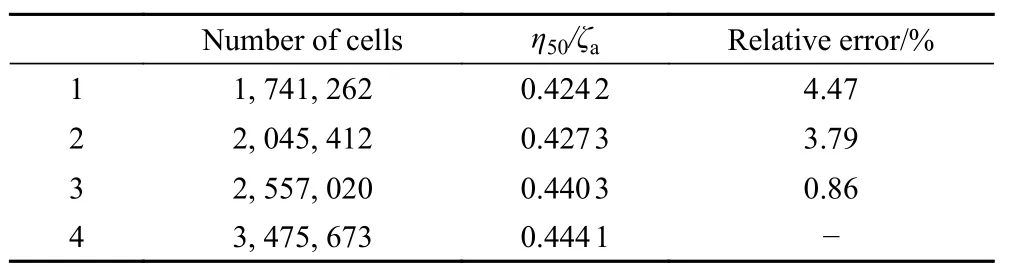
表2 网格无关性分析Tab. 2 Results of grid convergence study

4 数值仿真结果分析

为研究不同波浪周期T和波高H对波浪推进艇航速及水翼推进效果的影响，选取1.4 s，1.6 s，1.8 s 和2.0 s 四个波浪周期进行数值模拟。

为监测产生的波，在x=0 m，y=-2 m 位置处设置探针记录波面位移。从图5 的波面位移时历曲线中可以看到，在第5 个周期后，波面曲线基本保持稳定。

图5 T=1.8 s, H=7.2 cm 时的波面位移时历曲线Fig. 5 Time history of wave elevation (T=1.8 s, H=7.2 cm)

4.1 周期和波高对运动响应的影响

波浪推进艇在不同波浪周期和波高条件下的运动响应如图6 所示。可以看出，在顶浪条件下，波浪周期相同时，艇体的垂荡运动响应随波高变化影响较小，纵摇运动响应RAO 随波高增大而降低。波浪周期越小，纵摇运动响应随波高增大而降低的趋势越明显。这一结果是水翼随着艇体进行垂荡和纵摇运动时产生的阻尼效应造成的，上述纵摇运动响应的降低也说明了水翼能吸收艇体纵摇运动方向的能量。

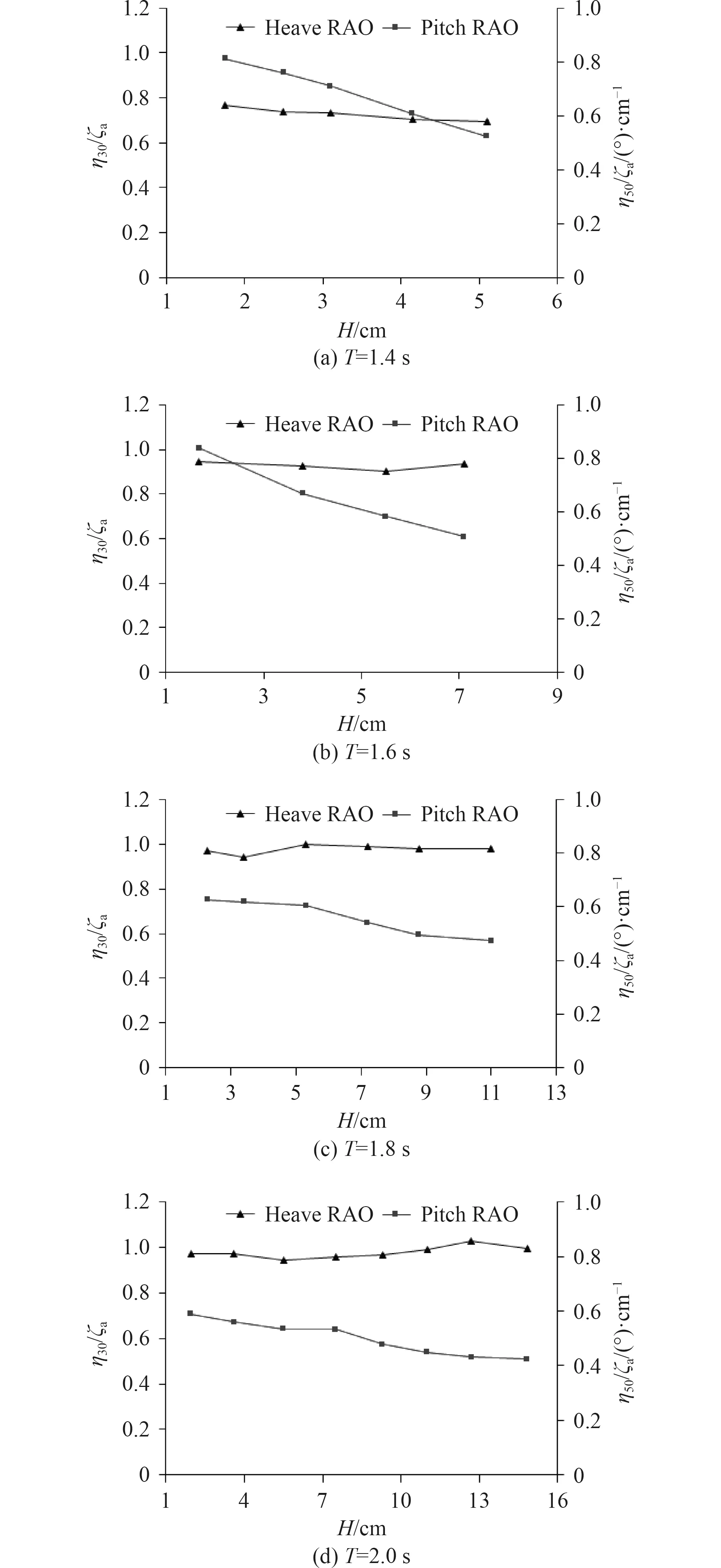
图6 不同波浪条件下运动响应Fig. 6 Motion response in different wave conditions

4.2 周期和波高对推力的影响

图7给出了波浪周期T=1.8 s 时水翼推力的时历曲线以及不同周期、波高条件下水翼的平均推力变化曲线。可以看到，在一个遭遇周期中，水翼有约75%的时间可以产生推力，并且观察到水翼推力存在2 个峰值，随着波高的增加推力峰值也在增大。图7（b）结果显示：波浪周期一定时，水翼产生的平均推力随着波高增大而增加；波高一定时，水翼产生的平均推力随着波浪周期增大而减小。

图7 不同波浪条件下的推力Fig. 7 Thrust in different wave conditions

图8为T=1.8 s，H=7.2 cm 时，在一个遭遇周期内水翼附近的涡量视图。可以看到，随着涡往下游传播其强度逐渐减弱，在所示波浪条件下，一个周期内水翼后缘有2 个涡脱落，逆时针旋转的涡位于顺时针旋转的涡上方，形成反卡门涡街。水翼产生的推力随着涡的增长和脱落过程而变化，当后缘涡开始脱落，新的前缘涡逐渐生成，水翼产生的推力逐渐减小，甚至会产生阻力。随着后缘涡的完全脱落且不断向后传播，前缘涡的不断增长，水翼产生的推力也随之增长。这表明涡的排列形式和发展过程对水翼性能影响很大。

图8 T=1.8 s，H=7.2 cm 水翼涡量视图Fig. 8 Vortex diagram of hydrofoils(T=1.8 s，H=7.2 cm)

4.3 周期和波高对波浪推进航速的影响

波浪推进艇在顶浪规则波中的平均推进航速如图9所示。可以看到，波浪推进艇在迎浪规则波条件下，在一定波高范围内可以使无人艇向前航行，且航速受周期和波高影响较大。在周期相同时，航速随着波高的增大先增加，在某一波高处达到最大航速，而后随着波高增大而迅速减小。这是因为顶浪航行时，当波高超过最佳波高后，波高增大引起的艇体阻力增加大于水翼产生的推力增量。