一种满刻度无溢出的圆周旋转CORDIC算法

刘立业，伍小保

(中国电子科技集团公司第三十八研究所，安徽 合肥 230088)

1 CORDIC算法简介

CORDIC是用于计算广义矢量旋转的一种迭代方法,为这类基础运算提供了一种有效、简单的硬件实现方法。该算法是由J.D.Volder于 1959 年提出的[1],可以将多种难以用硬件电路直接实现的复杂运算分解为统一的简单移位、加迭代运算[2]。

设变量(Xi-1,Yi-1)旋转角度kiαi，ki=±1,之后得到新的变量(Xi,Yi)为:

(1)

选择αi=arctan(2-(i-1)),即tanαi=2-(i-1)，则：

(2)

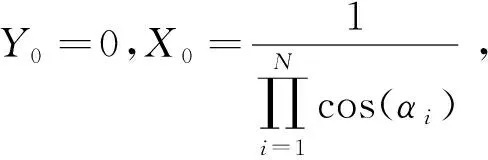
(3)

基带数字处理中，常用CORDIC算法产生基带I/Q信号，由式(3)可知，在二进制表示下，可以用移位操作得到目标角度Z0的余弦值XN和正弦值YN。

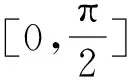
2 误差来源分析

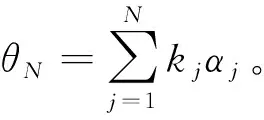
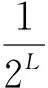
如果最后一级发生了溢出，计算结果从7f fff变成了80 000(假设处理位数20位)，会导致输出1～-1的极大错误；如果该溢出发生在中间第i级运算，在CORDIC算法的特色操作——右移i-1位过程中，本应该左补i-1个0，现在变成了左补i-1个1，带来了1/2i-2的误差，该误差将会往后传递影响输出精度。

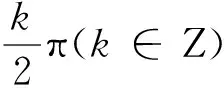
3 解决方法

分析产生溢出的2种情况可以发现，发生溢出后，错误值的绝对值和准确值差别很小，因此可以根据理论余弦(正弦)值的正负符号对输出结果进行修正——如果输出和理论值不同符号，强制改变输出的符号(不改变绝对值)。本文中，非最后一级的结果由构建的当前角度来修正，最后一级由初始相位来修正(赋值)。纠正误差过程如图1所示。

图1 误差纠正框图

3.1 象限映射

本文采用的方案里，4个象限的映射依据分别为：

(4)

由正余弦函数的性质可知，本方案象限映射过程只改变了正余弦值的符号，不改变绝对值。

3.2 非最后一级的修正

为了得到每级算法的理论值，本文构建当前角度θi，对每一级的输出相位理论值做跟踪：

(5)

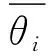
(6)

(7)

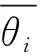
(8)

(9)

3.3 最后一级的修正

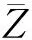
(10)

(11)

4 效果和结论

本文方法消除溢出的仿真效果如图2～4所示。

图2为修正前的仿真效果图。从中可以看到，在零相位(左下圈圈)处发生溢出，输出cos值本应该是+1，现在变成了-1。

图3为只做赋值模块的修正(上述第4步)时的仿真效果图。可以看到，零相位(左下圈圈)处的溢出已经被纠正，但是π/2相位(右上圈圈)处中间某级CORDIC迭代过程发生溢出，导致最终输出误差较大。

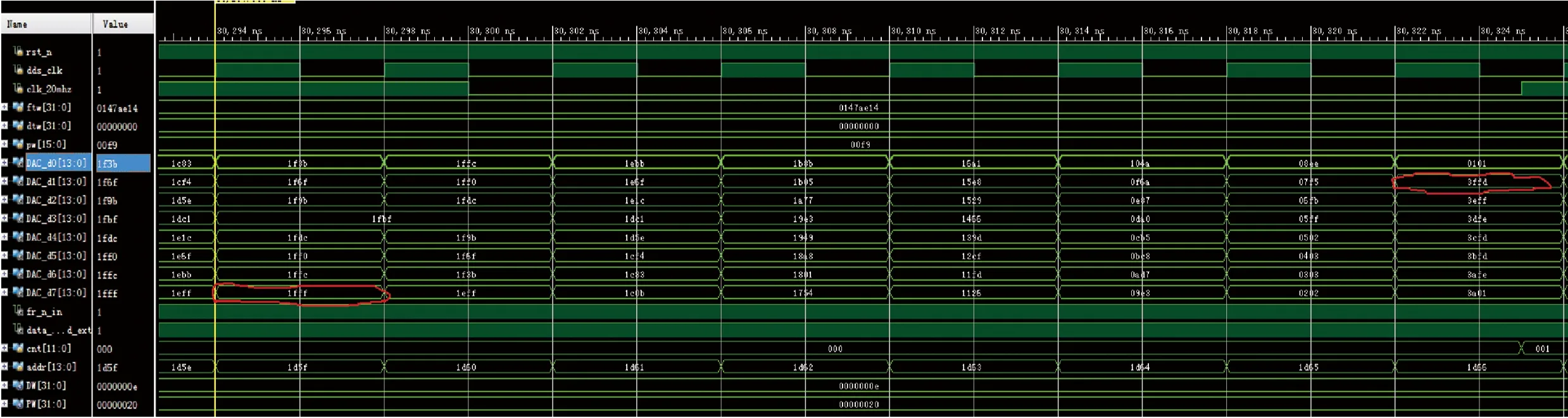
图3 只做赋值模块修正时仿真效果示意图

图4为做完完整修正步骤后的仿真效果图。可以看到2处的溢出均已被消除。同时还可以看到，输出覆盖2000(14位补码表示的-1)至1fff(14位补码表示的1)，因此输出是满刻度的。

图4 完整修正后仿真效果示意图

综上所述，本发明解决了圆周旋转CORDIC算法溢出问题，严格控制了算法的输出误差，精确、满刻度地产生了任意相位的正余弦值，同时该算法简单，占用资源少，在实际的DA电路中具有较大的应用意义。