基于噪声训练的转发式干扰机数字自干扰对消

鲁人杰，蒲书缙，赵忠凯

(1.哈尔滨工程大学，黑龙江 哈尔滨 150001；2.中电防务科技有限公司,四川 成都 610051)

0 引 言

转发式干扰机通过对目标信号的接收、存储、调制再转发的流程，可以对敌方雷达施加压制干扰或欺骗干扰等相参干扰，相较于传统的非相参干扰方法，干扰效果更佳。因为转发式干扰机发射信号和接收信号存在高度相关性，在收发同时工作时，发射信号不可避免地会对接收机造成自干扰。尤其对于小型化干扰平台而言，其发射和接收天线之间的距离很短，自干扰信号功率相较于目标信号功率往往高好几个量级，影响接收机的正常工作[1]，严重时甚至会产生自激[2]。为了消除自干扰的影响，转发式干扰机一般采用间歇采样工作方式，即发射机和接收机分时工作。采用此种工作方式虽然能够避免自干扰影响，但影响了干扰机的整体性能。一方面降低了对目标信号的侦察概率，另一方面降低了干扰性能[3]。

自干扰对消技术是根据参考信号估计出干扰信号，并将估计信号从实际自干扰信号中减去，可以有效地抑制进入接收机滤波器通带中的自干扰[4]，已被广泛应用于移动通信[5-6]、水声通信[7-8]及雷达[9-10]等众多领域。目前的自干扰对消研究一般从空域、射频域和数字域3个方面展开，而数字域对消因其精确的信道估计与灵活丰富的数字信号处理算法成为主要的研究方向[11]。无论是常规信道估计方法还是自适应滤波方法，对干扰信道的准确估计都是数字自干扰对消的重要步骤[12]。

文献[13]通过在大功率发射机的发射端引入导频信号，实现干扰的有效对消，但其针对的是信号的同频噪声干扰，是基于干扰与有用信号不相关的前提来展开的。文献[14]将全双工系统的通信过程分为训练阶段和数据传输阶段，并评估了不同导频序列与导频功率对干扰对消性能的影响，但是其训练模式只传输导频序列进行信道估计，而转发式干扰机的自干扰对消需要考虑目标信号对信道估计的影响。文献[15]提出一种基于深度学习的信道估计网络，使用神经网络提取信道响应特征矢量，但其离线训练步骤实时性差，且网络复杂，不易于硬件实现。文献[16]和[17]则主要关注无线中继领域的全双工系统实现，前者采用正交导频法和最小二乘法估计信道状态信息，后者采用盲估计法避免了基于导频方法的额外开销。

不论是基于导频还是盲估计的方法，高度相关的自干扰信号与目标信号的叠加都会使信道估计变得困难，而错误的信道估计会直接造成算法对消性能急剧恶化。因此两者虽然都通过改进方法减少了信道估计的导频开销，但都不能直接用于干扰机的自干扰信道估计，需要研究适用于转发式干扰机的数字自干扰对消方法。

针对以上问题，本文提出了一种基于噪声训练的数字自干扰对消方法，其创新之处在于：(1)以限带高斯白噪声训练得到的系数用于对消干扰机工作时的转发式自干扰，避免了传统自适应算法因目标信号与干扰信号高度相关造成的算法失效问题;(2)训练过程中，考虑了目标信号存在的影响，不需要为训练过程额外分配时隙，使干扰机可以收发同时工作，提高工作效率；(3)训练系数对于不同信号调制类型、不同频率自干扰的对消性能鲁棒性好。

1 转发式自干扰对消模型

如图1所示，干扰机发出的转发式干扰信号会通过多径信道耦合至接收机，影响接收机的正常工作，这里的多径信道更符合莱斯信道，从发射天线到接收天线既包含直射路径，也包含经过折射或者衍射到达的路径。一般情况下，干扰机收发端相对位置固定，信号的衰落效应相比于发射频率本身是缓慢的，自干扰信道参数在一定时间内是恒定的，基于此对信道进行估计。所提训练对消方法作用于数字域自干扰对消，所以在讨论时忽略射频域及空域部分的影响是合理且必要的，后面提到的接收信号都认为是已经经过空域和射频域干扰对消的信号。同时，考虑干扰机的工作特点，由于雷达目标信号为非合作信号，训练过程可能会受到目标信号的影响，且其频率、功率、调制类型随机多变，因此训练时应考虑雷达目标信号可能带来的影响。

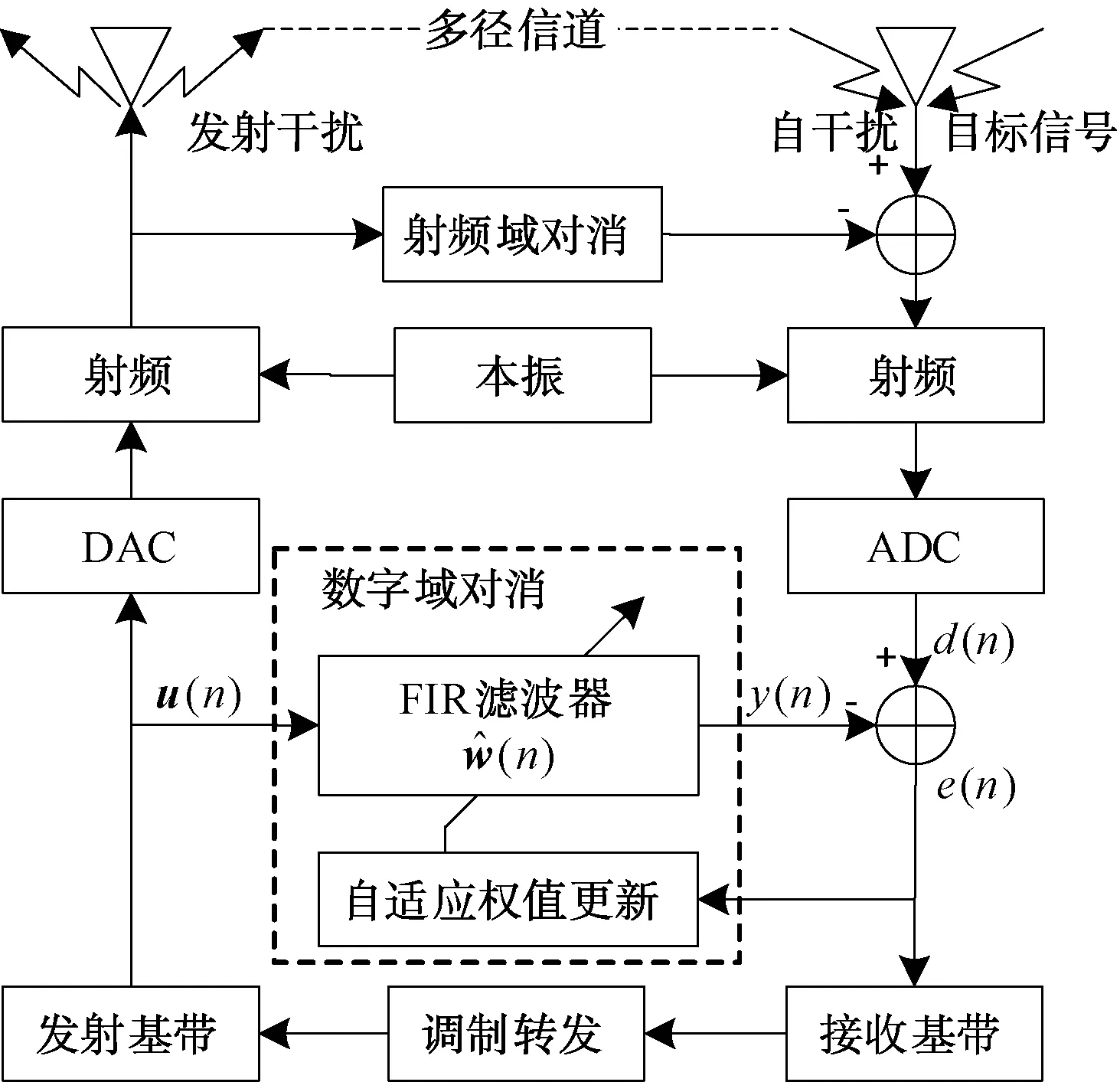
图1 转发式自干扰对消模型

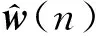
u(n)=[u(n),u(n-1),…,u(n-M+1)]T

(1)

式中：M为滤波器抽头数。

训练过程采用基于最小均方(LMS)算法的自适应滤波器结构实现，算法主要由以下2个相互关联的过程构成：

(1) 滤波过程

计算滤波器对抽头输入向量u(n)的估计信号y(n)：

(2)

将期望响应即接收信号与估计信号作差得到估计误差e(n)，即：

e(n)=d(n)-y(n)

(3)

(2) 自适应过程

(4)

2 噪声训练对消方法

本文设计的对消方法分为2个阶段，先是进行信道估计的训练阶段，然后是进行转发式自干扰对消的工作阶段。

对于训练阶段，在目标信号存在的情况下，发射限带高斯白噪声作为自干扰信号，估计出此时的自干扰信道参数。根据图1模型，构建图2所示的M阶自干扰重建滤波器，则信道估计的目的就是估计出均方误差意义上的最优有限单位冲激响应(FIR)滤波器权系数向量。

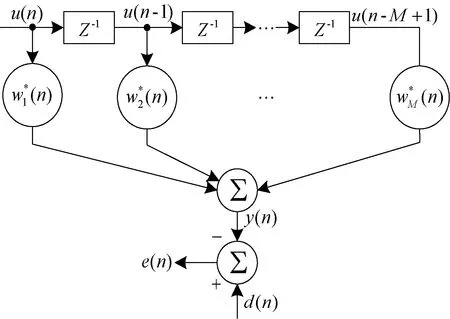
图2 M阶自干扰重建滤波器

定义目标信号与训练的噪声序列，目标信号为s(n)，噪声为ε(n)，训练发射的干扰信号为v(n)。v(n)是零均值的限带高斯白噪声，其功率谱密度满足：

(5)

此时，假定自干扰信道中延时为0,1，…，M-1的路径所对应信道系数分别为h0,h1，…，hM-1，则理论最优权系数向量w0、抽头输入向量u(n)及目标信号迭加训练噪声后的实际接收信号d(n)可表示为：

w0=[h0,h1,…,hM-1]H

(6)

u(n)=[v(n),v(n-1),…,v(n-M+1)]T

(7)

(8)

自适应滤波器对自干扰信道的系数估计过程可以概括为求解矩阵形式的维纳-霍夫方程[18]：

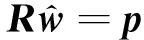
(9)

R=E[u(n)uH(n)]

(10)

p=E[u(n)d*(n)]

(11)

式中：R表示由横向滤波器抽头输入u(n)组成的M×M相关矩阵；p为抽头输入与接收信号的M×1的互相关向量。

将式(7)与式(8)代入式(10)、(11)，得到此时的R与p为：

(12)

(13)

而式(13)中的每一项v(n)d*(n)展开为：

E[ε*(n)v(n)]

(14)

因为训练时自干扰信号是预设的与目标信号相互独立的随机序列，两者不相关，其互相关函数值为0，且干扰与噪声不相关，则:

(15)

若系统采样率为fs，假定训练时采用限带高斯白噪声的W为fs/2，即当训练噪声占满信道带宽时，由于限带高斯白噪声的自相关函数rv(t)是一个抽样函数，其只在t=k/2W,k=1,2,3…时值为0，而此时的采样间隔为：

τ=1/fs=1/2W

(16)

因此，可得出以下结论：

(17)

此时算法的解即为反映信道特性的滤波器权系数向量为：

(18)

至此，训练阶段结束，训练序列不再作为干扰信号，进入工作阶段，转发对消结果作为干扰信号。则此时的抽头输入向量u(n)及实际接收信号d(n)更新为：

u(n)=[e(n),e(n-1),…,e(n-M+1)]T

(19)

(20)

(21)

e(n)=s(n)+ε(n)

(22)

式(22)表明：训练系数可以消除掉工作阶段中与目标信号同频的转发式干扰而且保留目标信号，达到了抑制转发式自干扰的目的。

3 仿真验证

3.1 评价指标

为了对所提方法的性能进行评价，采用均方偏差(MSD)和对消比(ICR)2个指标分别评价系数训练精度和干扰对消水平。MSD作为训练系数与最优权系数偏离程度的评价指标定义为:

(23)

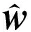
ICR能直接反映对消前后干扰抑制程度，定义为σICR:

(24)

式中：Pj为对消前自干扰信号功率；Py为对消后信号功率；Ps为目标信号功率。

3.2 训练效果影响分析

定义干噪比(INR)为σINR：

(25)

式中：Pit为接收的自干扰功率；Pn为噪声功率。

定义信噪比(SNR)为σSNR：

(26)

式中：Ps为目标信号功率;Pn为噪声功率。

仿真参数设置如下，干扰信号为限带高斯白噪声，带宽200 MHz，干噪比15 dB；目标信号为常规脉冲信号，信号频率为50 MHz，信噪比为15 dB，脉宽8 μs，脉冲重复周期40 μs；自干扰信道多径数为8，信道参数(最优权系数向量)设置为wo=[0,0,0,0.3,0.7,0.2,0,0]T，系统处理速率为245 MHz。仿真得到训练系数变化曲线，如图3所示。

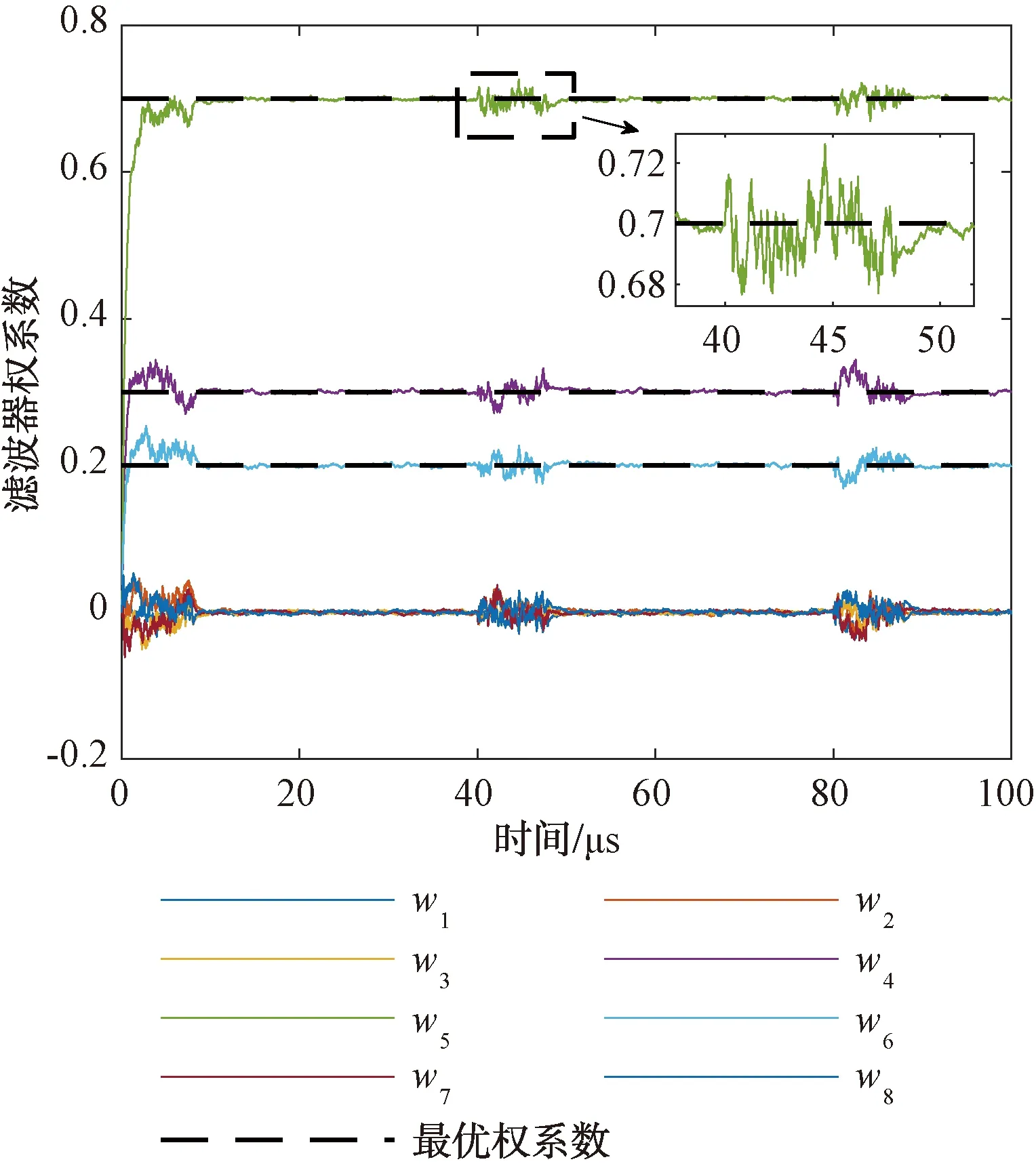
图3 训练过程系数变化

从图3可见，训练系数大约在5 μs处就能达到收敛，目标信号的存在并没有影响系数收敛的趋势和最终结果。但由仿真结果也可以看出，目标存在时，各个权系数在理论值附近随机游走，误差有所增加。这是因为LMS作为一种局部滤波算法是次优的，其算法本身受到梯度噪声影响，无法收敛至最优解，而会围绕最优解随机游走。这种随机游走的误差使得LMS算法需要遵循小步长理论，设置足够小的步长来最大程度减弱梯度噪声的影响[18]。而当遇到不相关的目标信号脉冲时，相当于又增加了额外噪声功率，估计系数围绕准稳态的随机游走现象更加凸显。

依据LMS的小步长理论，进一步减小算法步长可以减小目标信号对系数波动的影响，但只减小步长会极大地延长训练时间。而LMS算法的理论步长边界由输入信号的相关矩阵特征值决定，则步长受训练干扰影响，而与目标信号无关，因此将步长与干噪比的影响综合考虑。分别仿真不同干噪比及不同步长情况下的目标信号脉冲处MSD的变化，并设置相同条件下无目标信号训练的MSD作为标准训练，结果如图4所示。

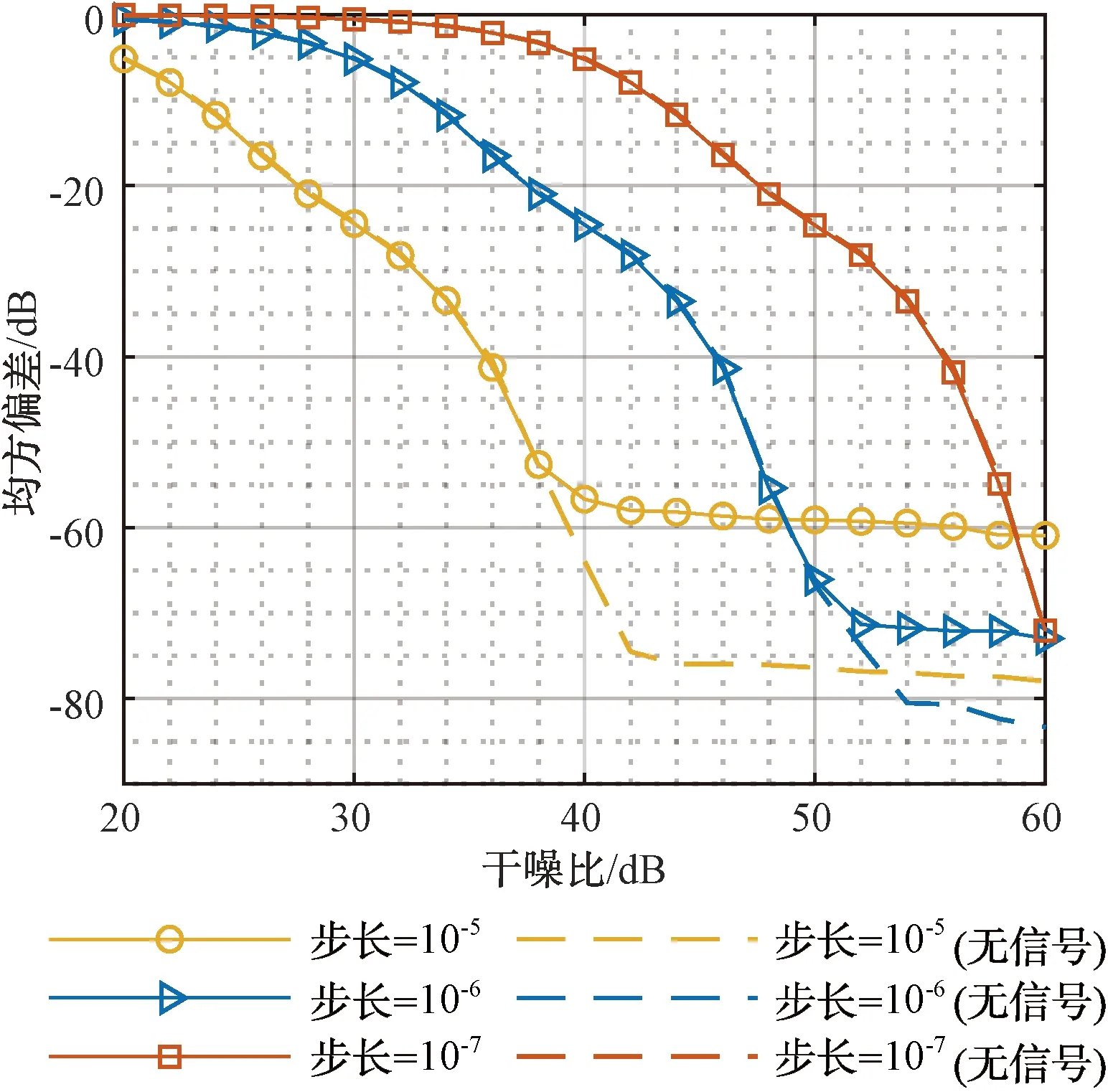
图4 干噪比和步长对MSD的影响

从图4可见，MSD受这2个因素的影响呈现明显规律性：其一，对于较小的干噪比，设置的仿真步长比其理论步长要小得多，算法收敛速度很慢，算法本身没有收敛到最优，时间成为此时最大的限制。但也因为此时步长偏小，目标信号对训练精度影响很小,训练效果符合标准表现；其二，对于较大的干噪比，其理论步长就比较小，设置的步长能使系数在训练时间内收敛，同时步长越小，MSD能达到的下限也越低。但所设步长相对此时的理论值不足够小，会使得目标信号的叠加影响变大，叠加训练效果变差，达不到标准训练效果。因此既要使算法本身能够收敛到最优系数，又要将目标信号带来的系数波动影响降到最低，在训练时间确定的前提下，应当遵循训练干噪比尽量大、算法步长在能收敛的前提下尽量小的原则。

由于目标信号来自于敌方雷达，其功率往往是在一个较大的范围内变化的，因此期望训练精度在一定信噪比范围内不受影响。分别设定干噪比为30 dB、40 dB和50 dB，仿真信噪比在10～30 dB范围内变化对应的MSD曲线，结果如图5所示。可见高干噪比不仅带来更高的训练精度，而且在干噪比与信噪比的差值(干信比)大于25 dB的条件下，即使面对信噪比变化的目标信号依然能有稳定的训练效果。

图5 干噪比和信噪比对MSD的影响

3.3 训练对消性能

在之前仿真的基础上，选择干噪比为50 dB的200 MHz限带高斯白噪声进行训练，此时目标为信噪比15 dB、频率50 MHz的常规脉冲信号。先对训练阶段进行仿真，对消前后的功率谱密度(PSD)结果如图6所示。从对消前后的功率谱可见，目标信号并没有对训练干扰对消产生影响，在目标信号得到保留的前提下能将自干扰抑制到接收通道的噪声限。

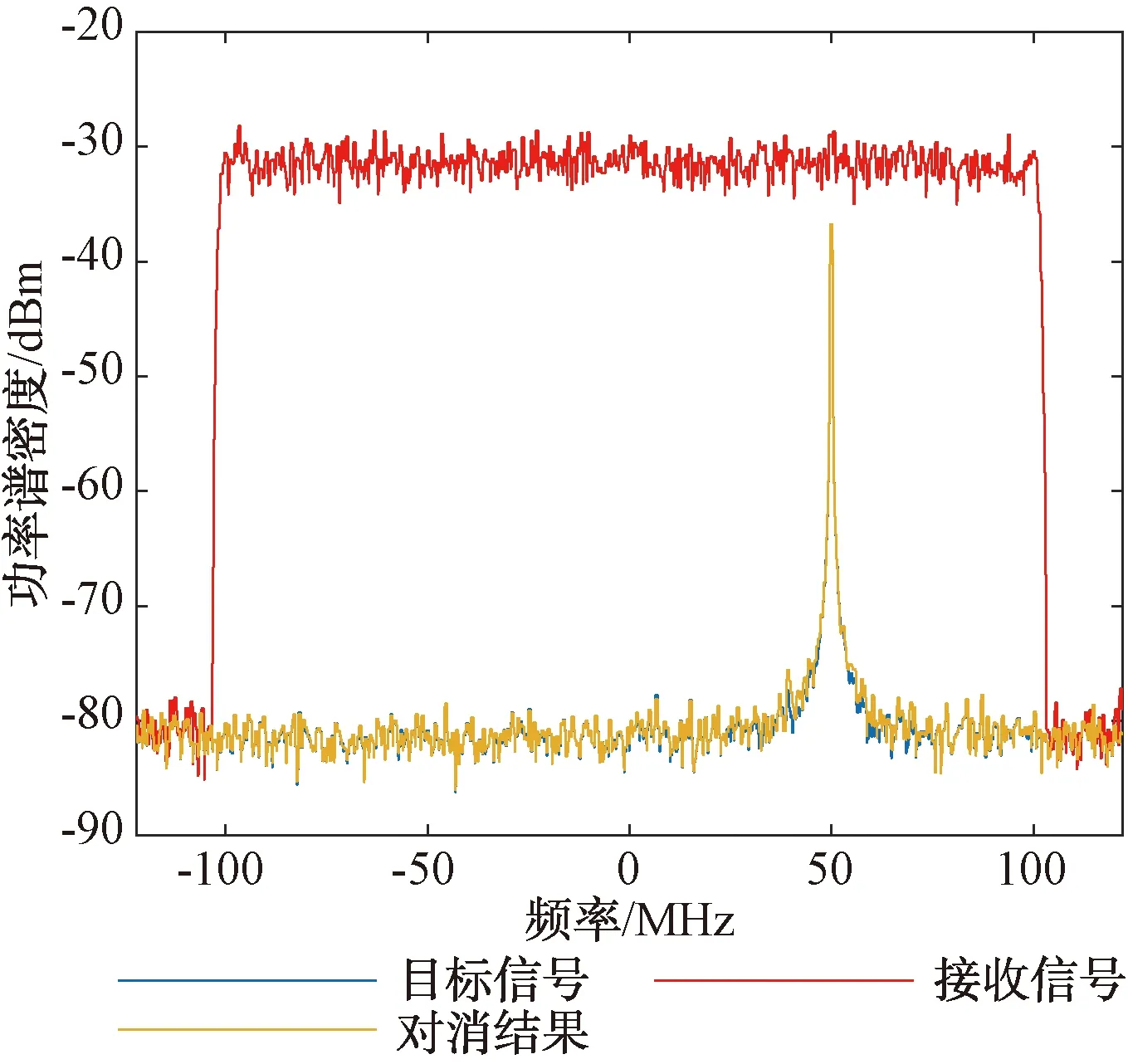
图6 训练阶段仿真功率谱结果

训练得到最优系数后，以50 MHz的常规脉冲目标信号为例进行工作阶段的仿真，仿真时考虑了实际存在的转发时延。

对消前后信号的实部和功率谱结果如图7(a)、图7(b)所示，从时域信号看，此时的系数可以对消转发的自干扰而不对目标信号产生影响；从功率谱看，此时的接收通道噪声限为-78 dBm，自干扰信号为-18 dBm，即干噪比为60 dB，对消后自干扰残余约为-73 dBm，则对消比约为55 dB，自干扰功率被抑制到接近噪声限。

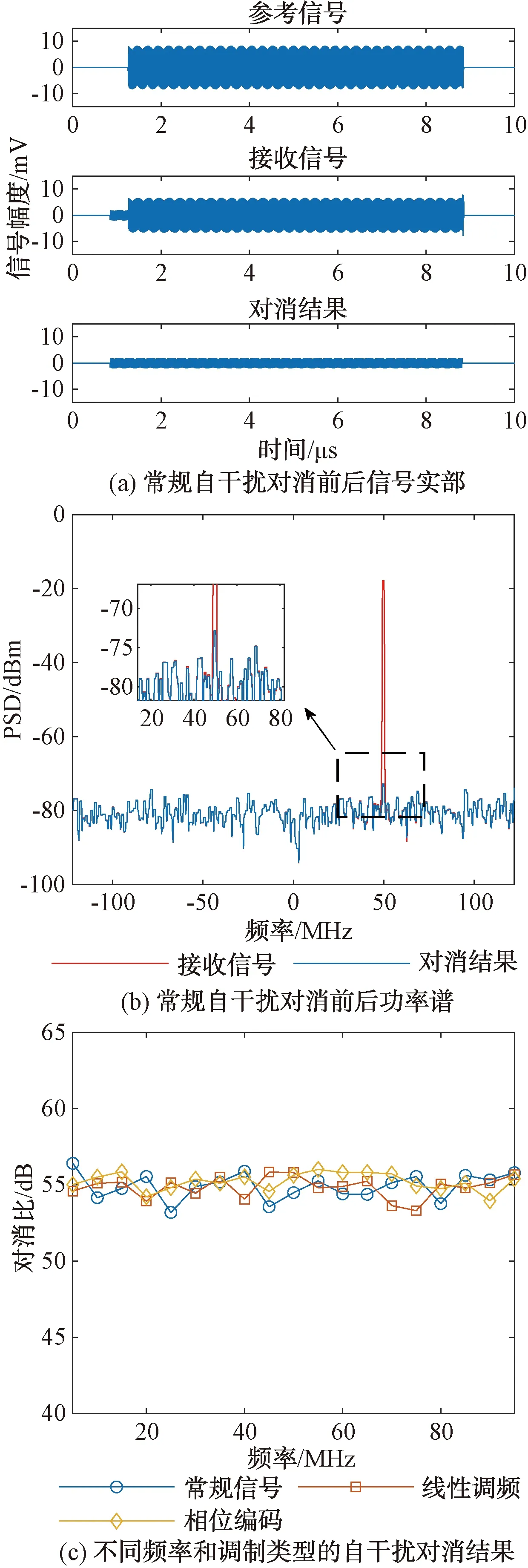
图7 工作阶段仿真

再产生与常规信号相同功率、带宽20 MHz的线性调频(LFM)信号和码元宽度250 ns的相位编码(BPSK)信号，对这3种目标信号样式分别在训练带宽范围内改变频率，多次仿真并计算对消比，汇总仿真结果如图7(c)所示。可以看出，对于不同频率和调制类型的目标信号，干扰对消比均能稳定在55 dB左右，且对消比整体偏差不超过2 dB,可见所提方法的鲁棒性较好。

4 硬件测试

4.1 测试条件

在仿真基础上，利用ADRV9009和ZC706搭建了干扰对消测试平台，如图8所示。其中，信号源模拟生成目标信号，功分器混合自干扰与目标信号，ADRV9009宽带射频收发模块发送与接收信号，ZC706的可编程逻辑(PL)部分实现训练对消算法处理，处理系统(PS)部分进行工作模式控制。

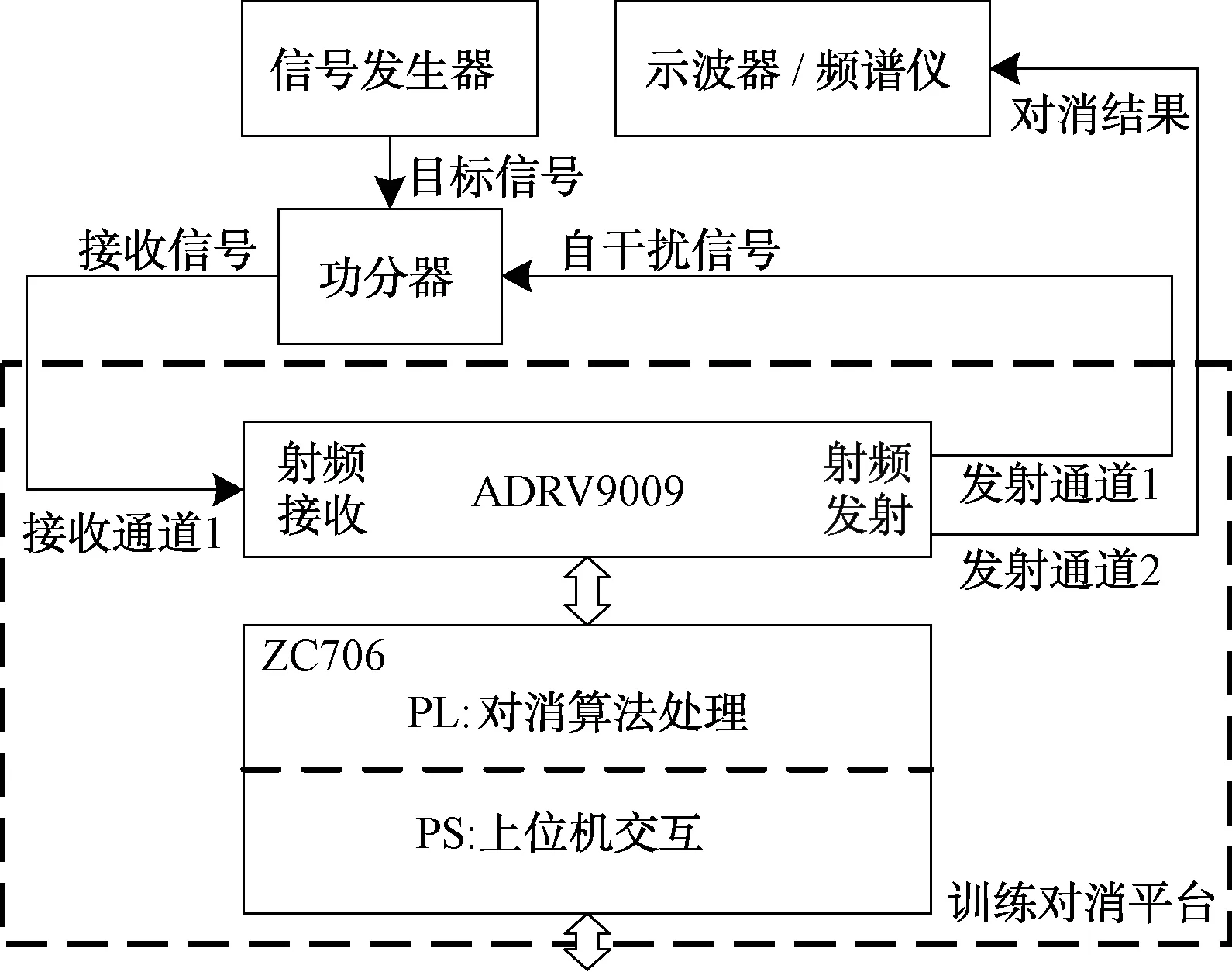
图8 测试平台

系统主要工作流程为：上位机先选择训练阶段，发射限带高斯白噪声作为干扰估计出自干扰信道系数；上位机切换到工作阶段，训练干扰不再输出，将接收信号进行转发作为干扰信号，利用训练锁存的系数对转发自干扰进行对消。主要测试参数设置如表1所示，同仿真一致，测试了常规信号、线性调频(LFM)、相位编码(BPSK)3种常见信号类型的自干扰对消情况。

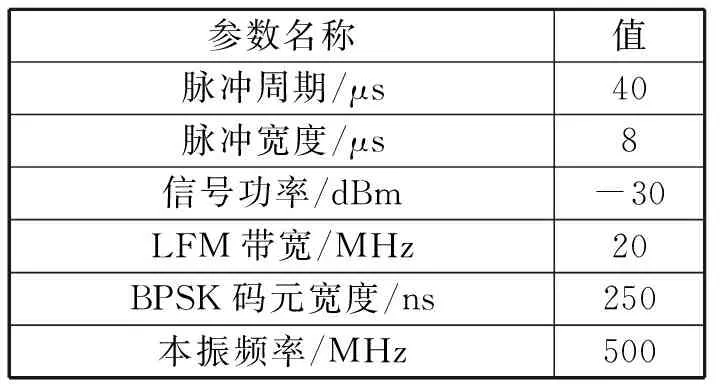
表1 测试参数设置

4.2 测试结果

通过Vivado软件的在线逻辑分析仪(ILA)实时观测接收信号和对消结果，测试结果如图9所示。

由图9可见，图中的上下2路信号分别为此时包含自干扰的实际接收信号和其经过对消的信号，比较对消前后的时域波形，可以直观地判断对消效果。该对消平台在不同输入信号时，均能够有效抑制自干扰信号，完成对目标信号的正常接收，实现了预期的自干扰对消功能。改变信号调制类型和中心频率，对干扰对消性能进行进一步的测试，测试结果如表2所示。

此时实际接收信号的干噪比约为60 dB，自干扰对消比整体稳定在52 dB左右，对消性能没有受不同信号调制类型和不同频率的影响。模数转换器(ADC)量化噪声、热噪声等实际因素限制了系统的实测对消性能，对消比水平稍低于仿真结果。但从整体来看，对消后，残余自干扰功率接近接收通道的噪声限，有效抑制了自干扰。

5 结束语

针对转发式雷达干扰机收发同时工作时存在的自干扰问题，本文设计了一种基于噪声训练的数字自干扰对消方法，并讨论了训练时不同干噪比、信噪比和算法步长对算法性能的影响。其仿真和硬件实测结果一致，该训练对消方法能有效抑制转发式自干扰，对消后残余自干扰功率接近接收通道噪声限。通过对不同频率和不同调制类型的信号进行测试可以发现，该自干扰对消方法鲁棒性好，并且可以有效避免目标信号与自干扰信号高度相关造成的算法失效问题。