舰艇编队反导作战中质心干扰运用策略研究
2023-03-24吴赐聪程志锋
吴赐聪,于 莹,程志锋
(海军工程大学,湖北 武汉 430033)
0 引 言
现代海战中,反舰导弹由于其射程远,精度高,威力大,一直是水面舰艇面临的主要威胁。当受到导弹末制导雷达跟踪时,舰艇实施质心干扰是有效的反导手段之一。实际运用中,单舰艇使用质心干扰可以达到较好的反导自卫效果;但编队条件下,使用质心干扰就很容易出现由于目标舰艇质心干扰不当而导致邻舰受到导弹二次威胁的情况。因此,舰艇编队使用质心干扰需满足一定条件,也就是编队质心干扰运用策略。
1 舰艇质心干扰引偏效果分析
当受到导弹威胁时,舰艇使用质心干扰会使导弹末制导雷达分辨单元内存在2个或2个以上的目标,进而使导弹转向跟踪由这数个目标共同构成的能量中心(质心),从而偏离舰艇方向[1]。干扰效果越好,则偏离角度越大。因此,理论上存在使导弹偏离角度最大的质心干扰发射角度[2-3]。
现建立三维直角坐标系,分析质心干扰最佳发射角度,如图1所示。
图1中,O、M′、T′分别表示舰艇、箔条云、导弹。O为坐标原点;λ表示导弹入射舷角;|OT′|=a0表示舰艇发现导弹时导弹与舰艇之间的距离;|OM′|=r0表示质心干扰的布放距离;D′表示舰艇O和箔条云M′的质心点;|OD′|=d0表示舰艇到质心点的距离。舰艇航向与y轴方向同向。α0为发射箔条弹的舷角(简称“发射舷角”,下同);θ0为导弹空间引偏角。
为便于计算和判断,将以上三维空间场景投影到水平面,M、T分别为箔条云和导弹在平面上的投影,平面图如图2所示。
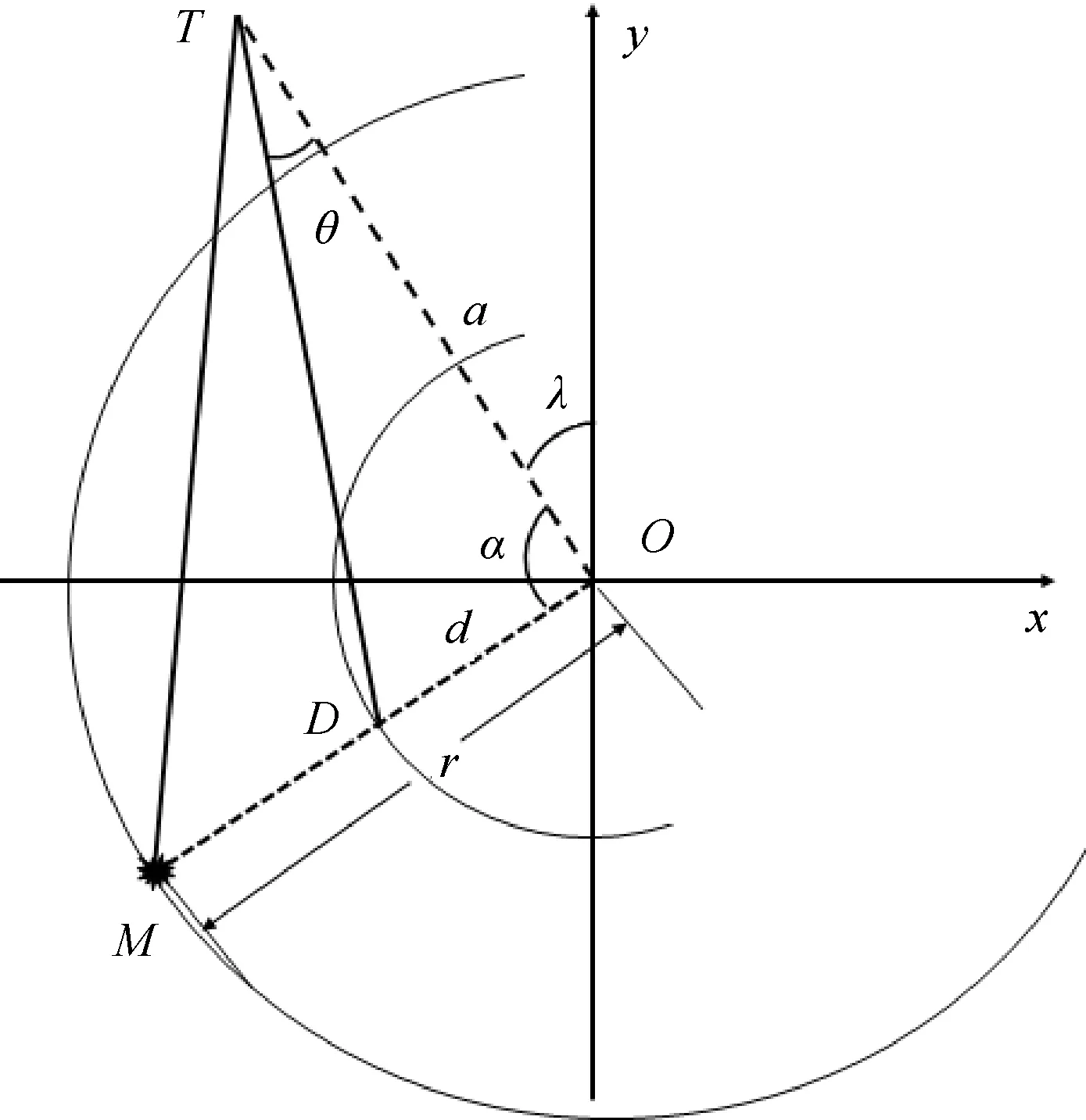
图2 质心干扰布设平面图
图2中,|OT|=a表示导弹发现舰艇并开始跟踪时导弹与舰艇之间的水平距离(简称“跟踪距离”,下同);|OM|=r表示质心干扰的布放水平距离;D为质心点D′的投影;|OD|=d表示舰艇到质心点的水平距离(简称“质心距离”,下同);θ0在水平面上的投影为θ(称为“引偏角”,下同)。α为由导弹入射方向转向箔条弹发射方向的夹角(简称“发射夹角”,下同)。由图1、图2可见,由于空间上的θ0与平面上的θ具有相关变化关系,并且实战中导弹一般都是低空掠海飞行,其高度远小于其跟踪距离,高度对θ计算结果的影响很小,所以投影到水平直角坐标系进行简化讨论是可行的。
任意时刻,若导弹已经发现并跟踪舰艇,则表示舰艇和导弹雷达均能发现对方,此时距离a可确定。当质心干扰样式确定时(布放距离、数量等),舰艇到质心点D的距离即质心距离d也可确定。由此,在ΔOTD中,有:
(1)
可计算得出引偏角为:
(2)
1.1 不同质心距离下的引偏效果
设跟踪距离a=20 km,当质心距离d分别取0.5 km、1.0 km、1.5 km时,可得发射夹角α与引偏角θ的关系,如图3所示。
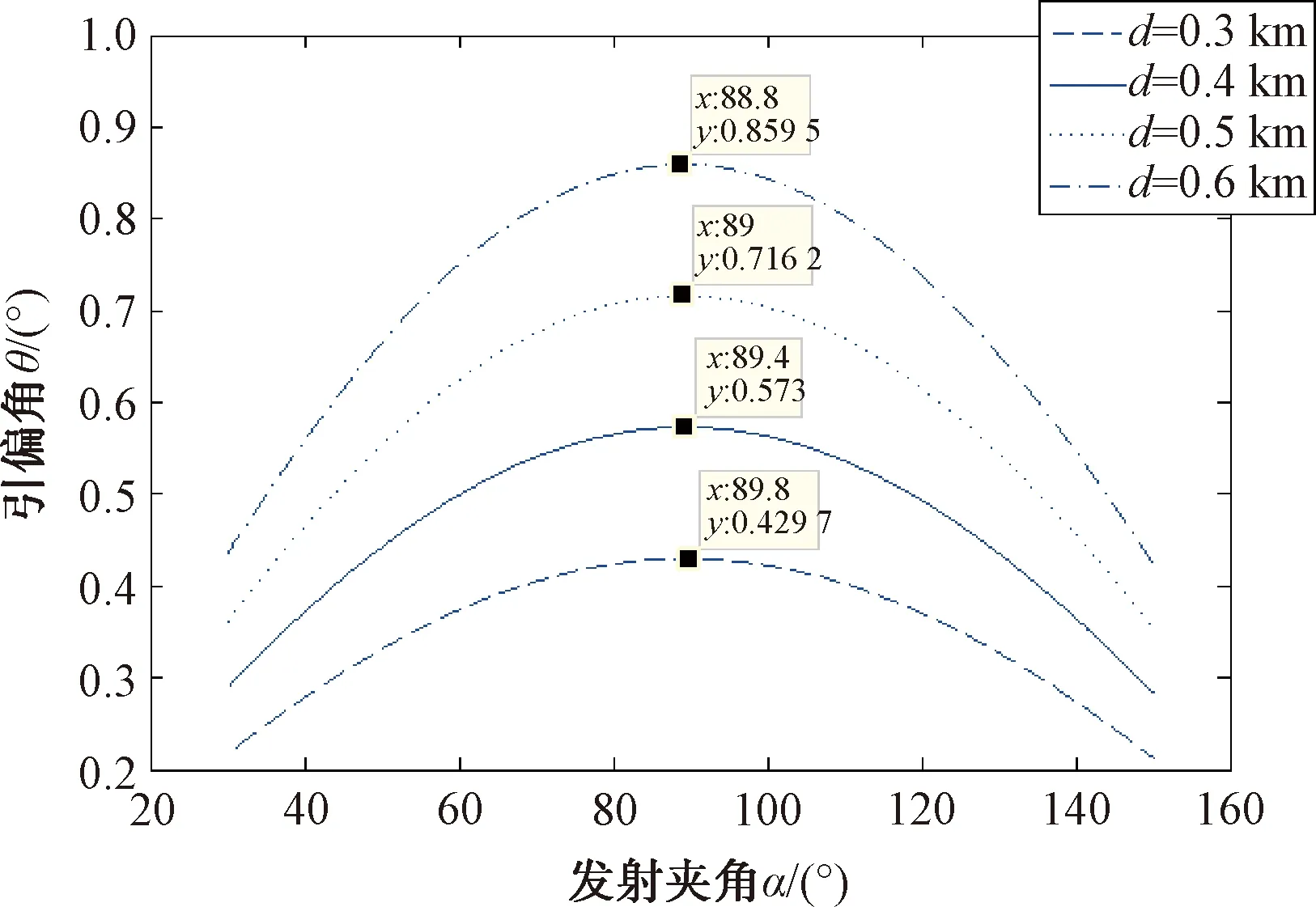
图3 不同质心距离时干扰发射夹角与引偏角关系图
由图3可见,质心距离d一定时,发射夹角α在70°~ 110°之间都有较好的引偏效果,最佳发射夹角在80°~ 90°之间,此时引偏角θ最大,即引偏效果最好;质心距离d取值不同的情况下,d越大,引偏效果越好。为便于描述,在此定义αe为最佳发射夹角,即在其他条件固定,仅有发射夹角α变化时,使得θ值最大的α(下同)。
1.2 不同跟踪距离下的引偏效果
设导弹的跟踪距离a分别为10 km、20 km、30 km、40 km,取质心距离d=1.0 km,可得发射夹角α与引偏角θ的关系,如图4所示。
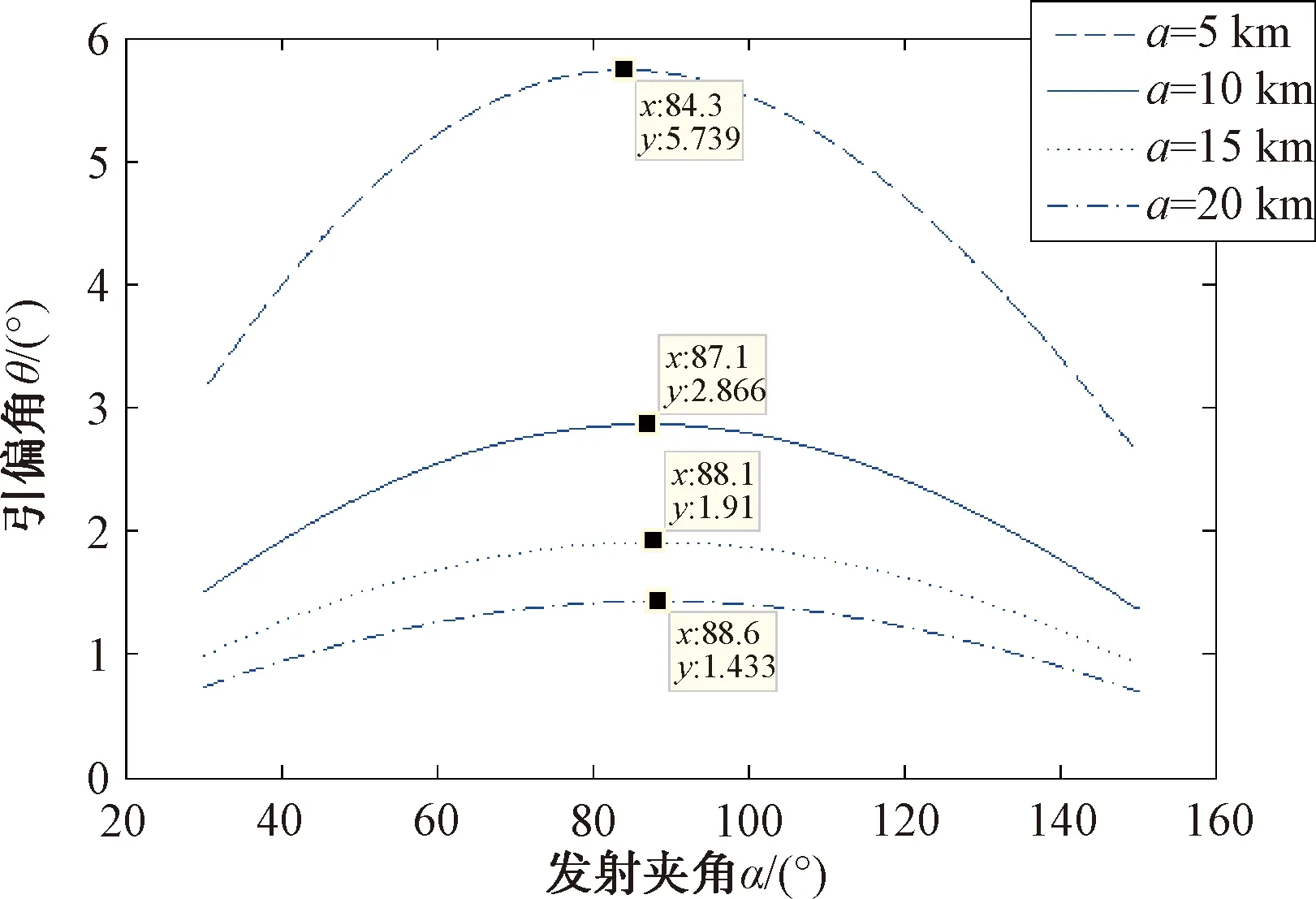
图4 不同跟踪距离时发射夹角与引偏角关系图
由图4可见,导弹跟踪距离a越大,相同条件下引偏角θ越小,使得引偏角θ取最大值的发射夹角α也越大。
2 舰艇实施质心干扰对邻舰的影响
实际上,在编队作战时,使用质心干扰必须要考虑对邻舰的影响。在此,假设编队内各舰艇具有同等重要性,如驱逐舰编队或驱护编队,而不存在优先被保护舰艇。
一般来说,某一舰艇发射箔条弹后,必定会出现这种情况:导弹末制导雷达波束内同时存在舰艇和箔条云,使得导弹由于质心效应而偏离原方向并向质心飞行。这种情况下,导弹可能会直接穿过质心,其末制导雷达波束锁定后方舰艇,或开启搜索雷达进行二次搜索。下文讨论即围绕此种情况展开。
质心干扰的释放时机是在导弹完成末制导搜索之后的跟踪阶段,这一阶段导弹与舰艇的距离通常不超过20 km,舰艇没有足够的时间机动,质心干扰对导弹的引偏角度一般较小,难以使导弹飞行方向彻底偏离整个编队。对于舰艇编队而言,一般在来袭导弹同侧实施质心干扰才可能有效引偏导弹(特别地,对于编队最前或最后的舰艇,发射与导弹异侧舷的箔条弹引偏效果更好),但同时存在导弹穿过质心点威胁编队其他舰艇的可能性。
舰艇编队基本战斗队形包括单纵队、单横队、方位队列、人字队列、菱形队列、环形队列等。本文选择其中有代表性的方位队列、人字队列进行讨论。图5、图6给出了方位队列、人字队列下质心干扰引偏导弹后威胁邻舰的情况。
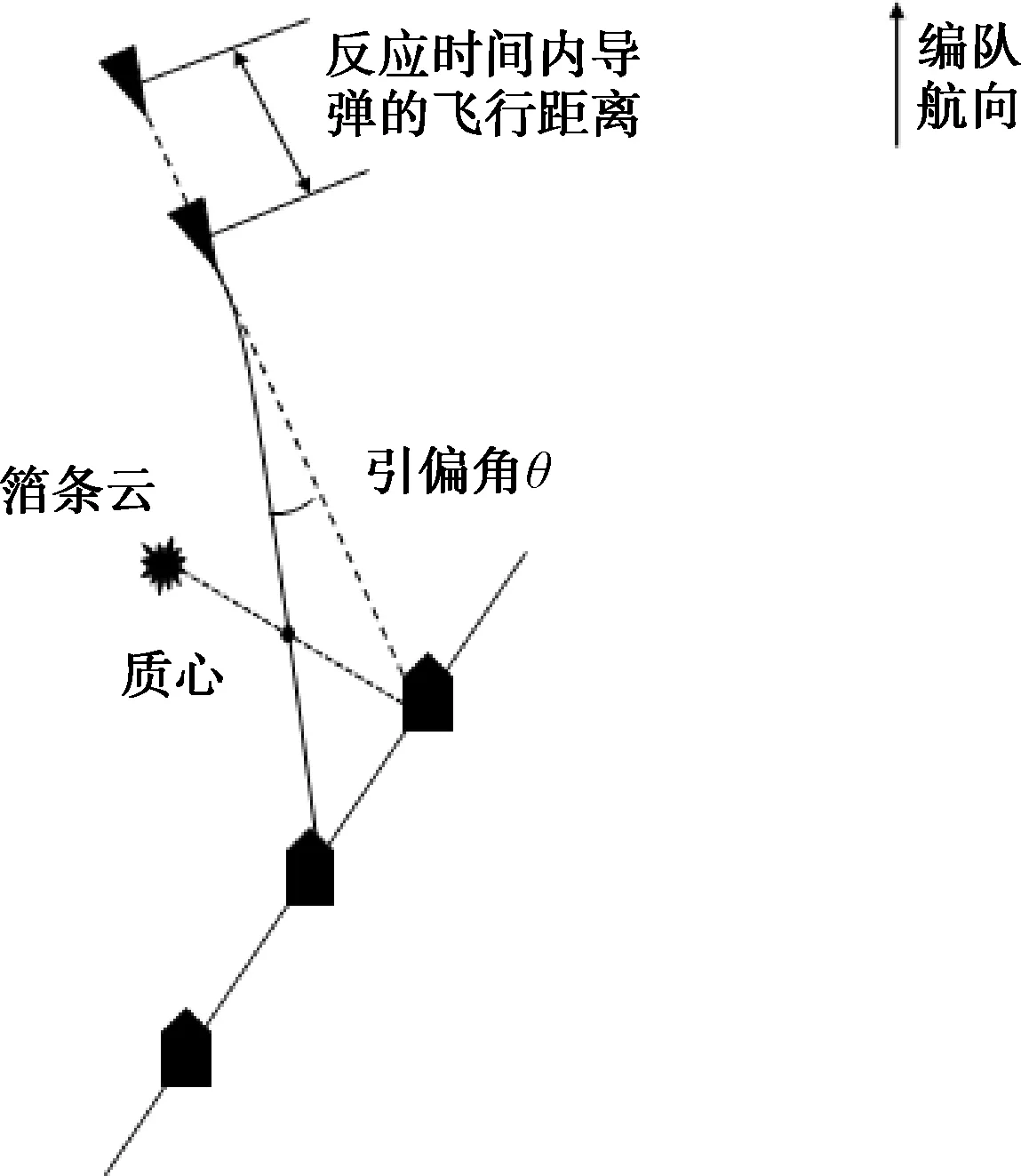
图5 方位队列下质心干扰导致邻舰被攻击示意图
3 舰艇实施质心干扰时避免对邻舰产生影响的策略
下面分别讨论在方位队列、人字队列下,舰艇实施质心干扰如何避免对邻舰造成威胁。
3.1 方位队列下的质心干扰策略
方位队列时,导弹可能被引偏飞向同侧邻舰,如图7所示。在该平面直角坐标系中,A、B、C分别表示方位队列下的3艘舰艇,T为来袭导弹,M为箔条云,λ表示导弹入射舷角,|AT|=a为跟踪距离,|AM|=r表示质心干扰释放距离,D为舰艇A和诱饵M的质心点,|AD|=d为质心距离,α为发射夹角,θ为引偏角,以上设置与前述相同。设|AB|=|AC|=b表示舰艇间距,β角为导弹被引偏后,其飞行方向与DB(质心点和后方舰艇连线)的夹角。
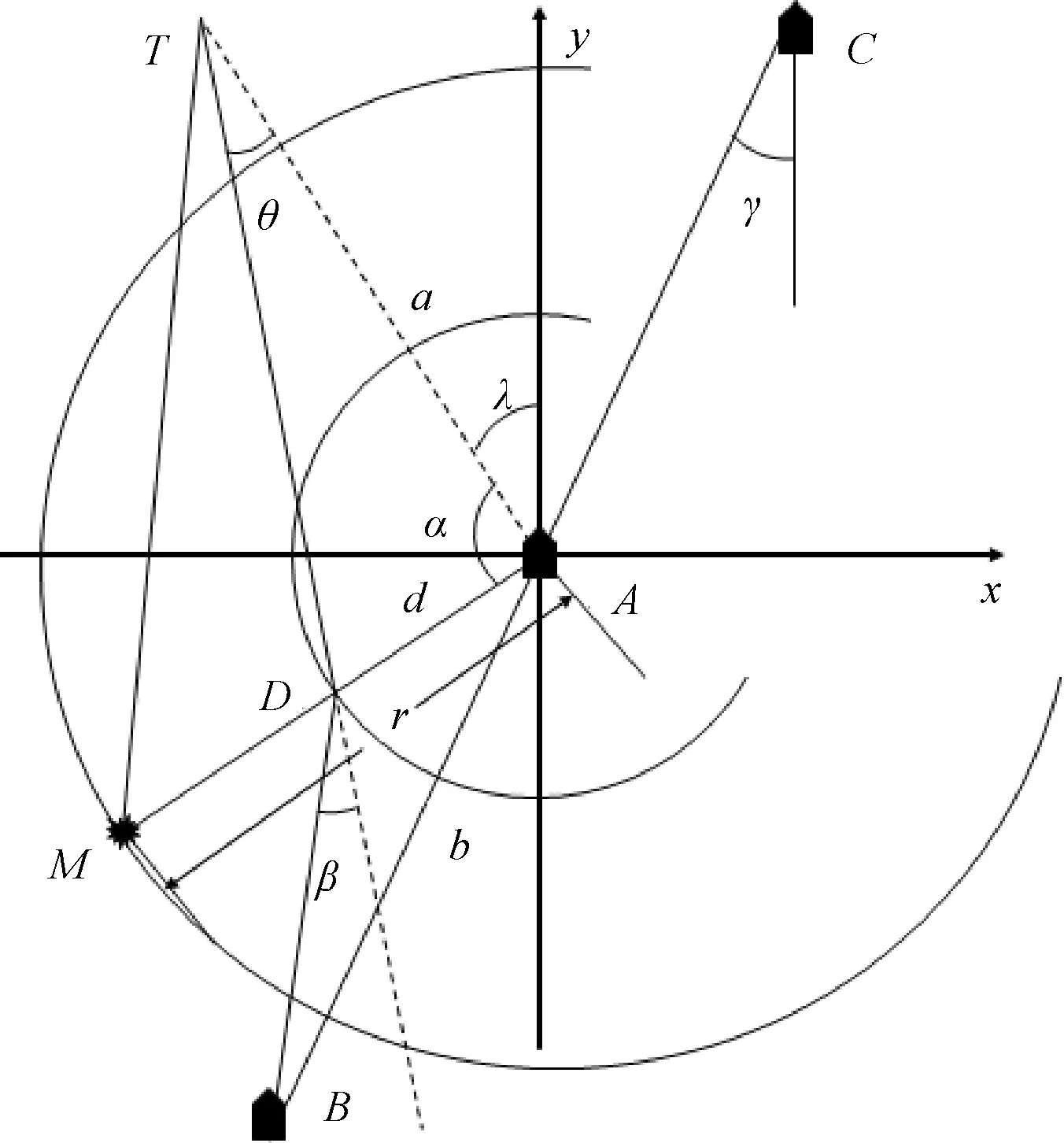
图7 方位队列下导弹攻击邻舰平面图
图7中,ΔABD具有如下角关系:
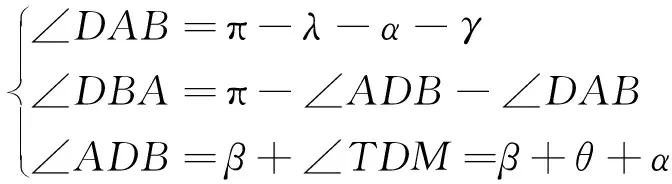
(3)
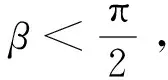
若舰艇使用与来袭导弹同侧的干扰弹,应满足λ+α+γ<π,否则质心干扰将在来袭导弹异侧舷发射,对导弹的引偏效果变差,导致目标舰艇自身容易受到导弹威胁。同时,30°<α+λ<150°,否则舰艇武器装备系统不能满足箔条弹发射需要(发射管旋转角度限制)。
利用正弦定理,在△ABD中得到如下关系式:
(4)
由式(3)和(4)计算得到β关于α的关系式:
(5)
式中:θ的算法同式(2)。
由式(5)可计算目标舰艇发射箔条弹方向的限制条件。
现假设跟踪距离a=20 km,舰艇编队队列角γ=30°,质心距离d=0.5 km,舰艇间距b=5 km,箔条弹允许覆盖的发射角度范围为30°~150°舷角。导弹入射舷角λ分别取30°、45°、60°、90°、120°时,计算可得β值,如图8所示。
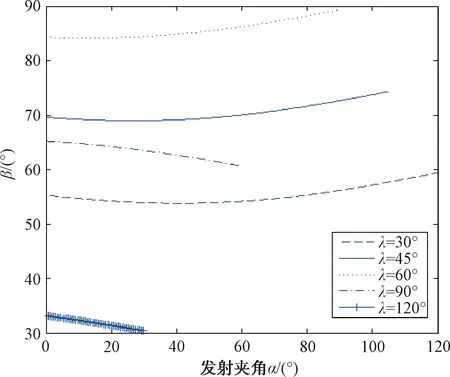
图8 入射舷角不同时导弹对邻舰的威胁随发射夹角变化图
由图8可分析得到如下结论:
(1) 当导弹入射舷角小于90°时,箔条弹的发射夹角α越大,越不容易使导弹威胁邻舰。但此时使得邻舰受威胁最小的发射夹角α与1.1节所述最佳发射夹角αe并不重合。因此,应兼顾导弹引偏效果保证目标舰艇安全的同时,尽可能减小对邻舰的威胁。在这2个要求下,发射夹角应根据实际情况来确定:当导弹入射舷角较小时,发射夹角α取值范围在80°~100°之间时,综合效果较好;当入射舷角较大但不超过90°时,发射夹角α应尽可能接近最佳发射夹角αe。
(2) 当导弹入射舷角大于90°时,发射夹角α越大,邻舰受到的威胁越大,其原因是此时效果较好的发射舷角α0将小于入射舷角λ。这种情况下,可能受到导弹二次威胁的舰艇变为C舰,用于判断B舰受威胁可能性的β消失,导致结果无法计算。若要继续判断C舰受威胁的可能性,则需重新计算角度关系,计算方法与前述方法相似,故不赘述。
(3) 假设导弹的跟踪波束范围为15°,由图8可以看出,导弹以任意角度入射时,β均大于导弹的半波宽度7.5°,因此在该队形下目标舰艇使用质心干扰几乎不会对邻舰造成二次导弹威胁;若导弹开启二次搜索,其搜索波束范围为120°,在导弹以小于45°舷角入射时,存在β小于半波宽度60°的情况,目标舰艇进行质心干扰可能导致邻舰受到二次导弹威胁,需要邻舰同时采取导弹抗击措施。
3.2 人字队列下的质心干扰策略
人字队列时,导弹可能穿过这种复式队形的一侧,击中另一侧,如图9所示。该人字队列左右队列角相同,设其余条件均与3.1节的方位队列情况下相同。图9为人字队列下导弹攻击邻舰效果图。
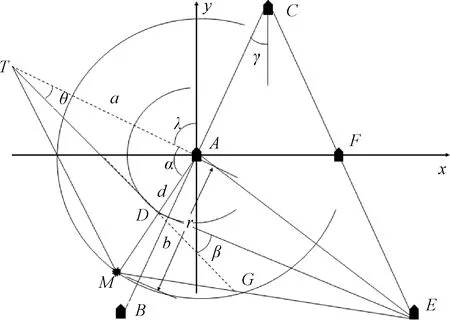
图9 人字队列下导弹攻击邻舰效果图
据图9可以判断:β较大时,计算结果与3.1节结果类似,因此这里不做重复讨论;β较小时,会对E舰造成威胁。β的计算式为:
β=arccos∠MDE-(π-θ-α)
(6)
式中:
(7)
△DEM、△ACE、△ADE中存在以下边长关系:
(8)
在△ACE、△ADE中,存在以下角度关系:
(9)
式中:∠MAB>0,即α+λ+γ<π,若不满足该条件,质心干扰将在来袭导弹异侧舷发射,对导弹的引偏效果变差,导致目标舰艇自身容易受到导弹威胁;且α+λ>30°,否则舰艇武器系统不能满足质心干扰发射需要(发射管旋转角度限制),此部分的限制条件也与方位队列情况下相同。
由式(6)~式(9),求得β关于α表达式为:
(π-θ-α)
(10)
(11)
引偏角θ的计算同式(2)。
现假设导弹跟踪距离a=20 km,舰艇编队队列角γ=30°,舰艇到质心点的距离d=0.5 km,舰艇间距b=5 km,箔条弹发射舷角范围为30°~150°。导弹入射舷角λ分别取30°、45°、60°、90°、120°,计算可得β值,如图10所示。
由图10可分析得到如下结论:
(1) 导弹以不同入射舷角λ攻击目标舰艇,λ较小时,发射夹角应取得范围在80°~100°之间较好;若入射舷角较大但不超过90°时,发射夹角应尽可能接近最佳发射夹角αe。此部分结论也与3.1节类似。
(2) 当发射夹角小于90°时,发射夹角的起始值并非从0开始,这是因为此时若以一个小角度发射质心干扰,导弹引偏后受威胁的舰艇变为F舰,需重新计算角度关系。
(3) 假设导弹的跟踪波束范围为15°,由图10可以看出,导弹入射舷角在60°~90°时,β小于半波宽度7.5°,即目标舰艇使用质心干扰容易对邻舰造成2次导弹威胁;若导弹开启2次搜索,其搜索波束范围为120°,导弹在小于90°舷角时入射,因β均小于搜索半波宽度,可以认为必然会再次搜索到E舰;而在入射舷角大于90°时,效果较好的发射舷角α0将小于入射舷角λ,又容易导致C舰被导弹搜索跟踪,因此需要这些舰艇同时采取导弹抗击措施。由此可见,复杂队形的舰艇编队,在强化了打击能力的同时,也增大了反导的难度,这对编队整体的协同能力是很大的考验。
利用公式(10),也可以讨论其他条件变化时,舰艇质心干扰的布设策略。设导弹入射角为λ=45°不变,改变队列角γ、跟踪距离a、舰艇间距b等参数,再按上述步骤计算β值,可以得出如下结果和结论:
(1) 跟踪距离越大,被引偏的导弹越容易发现E舰,如图11所示。这是因为跟踪距离越大,导弹的雷达视野范围越广,导弹到A舰、E舰连线的夹角越小,那么引偏后,导弹越容易在雷达波束内发现E舰。
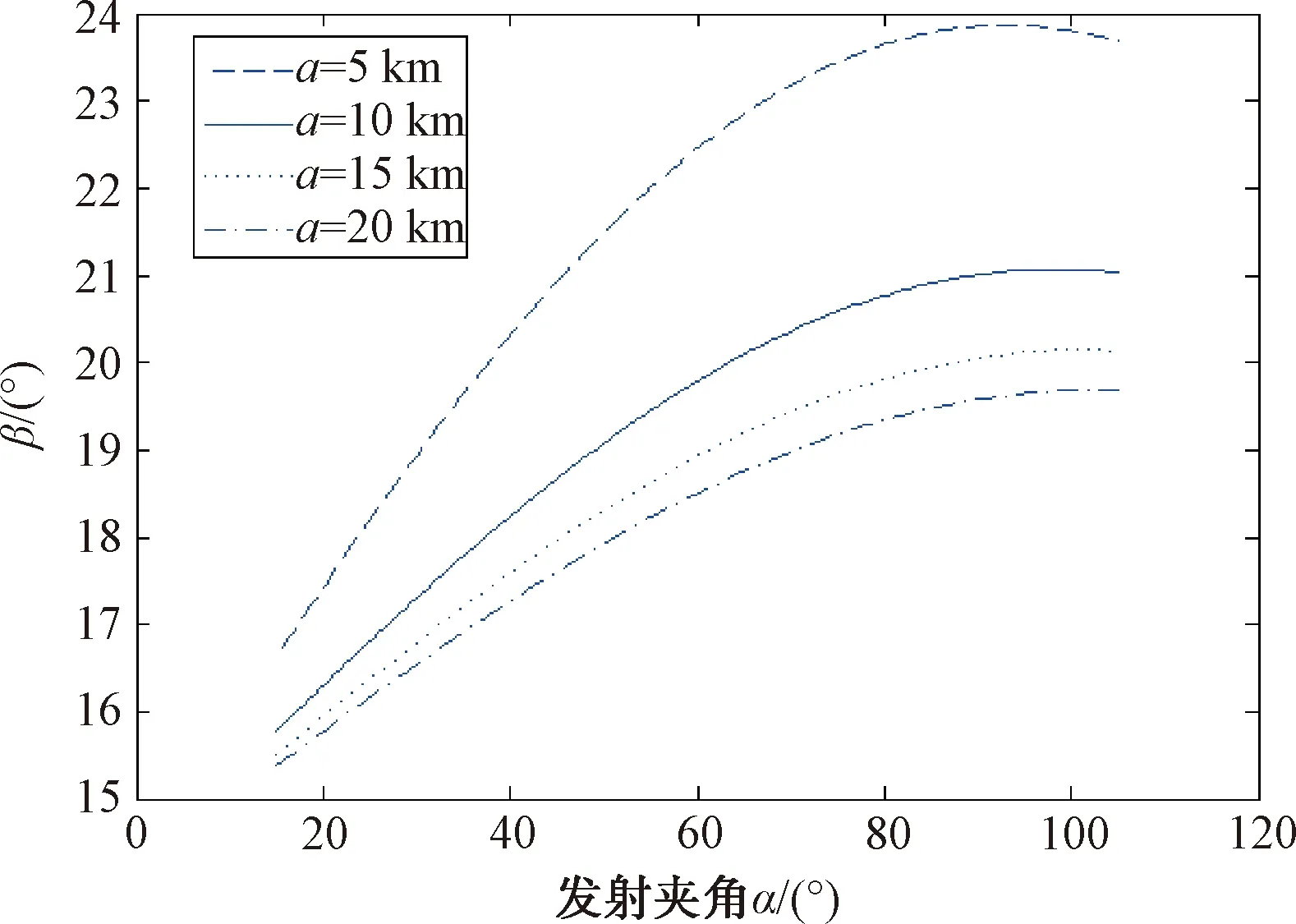
图11 跟踪距离不同时导弹对邻舰的威胁随发射夹角变化图
(2) 适当增大舰艇队列角γ,使得E舰能有效地远离导弹雷达波束范围,有利于避免导弹威胁,如图12所示。
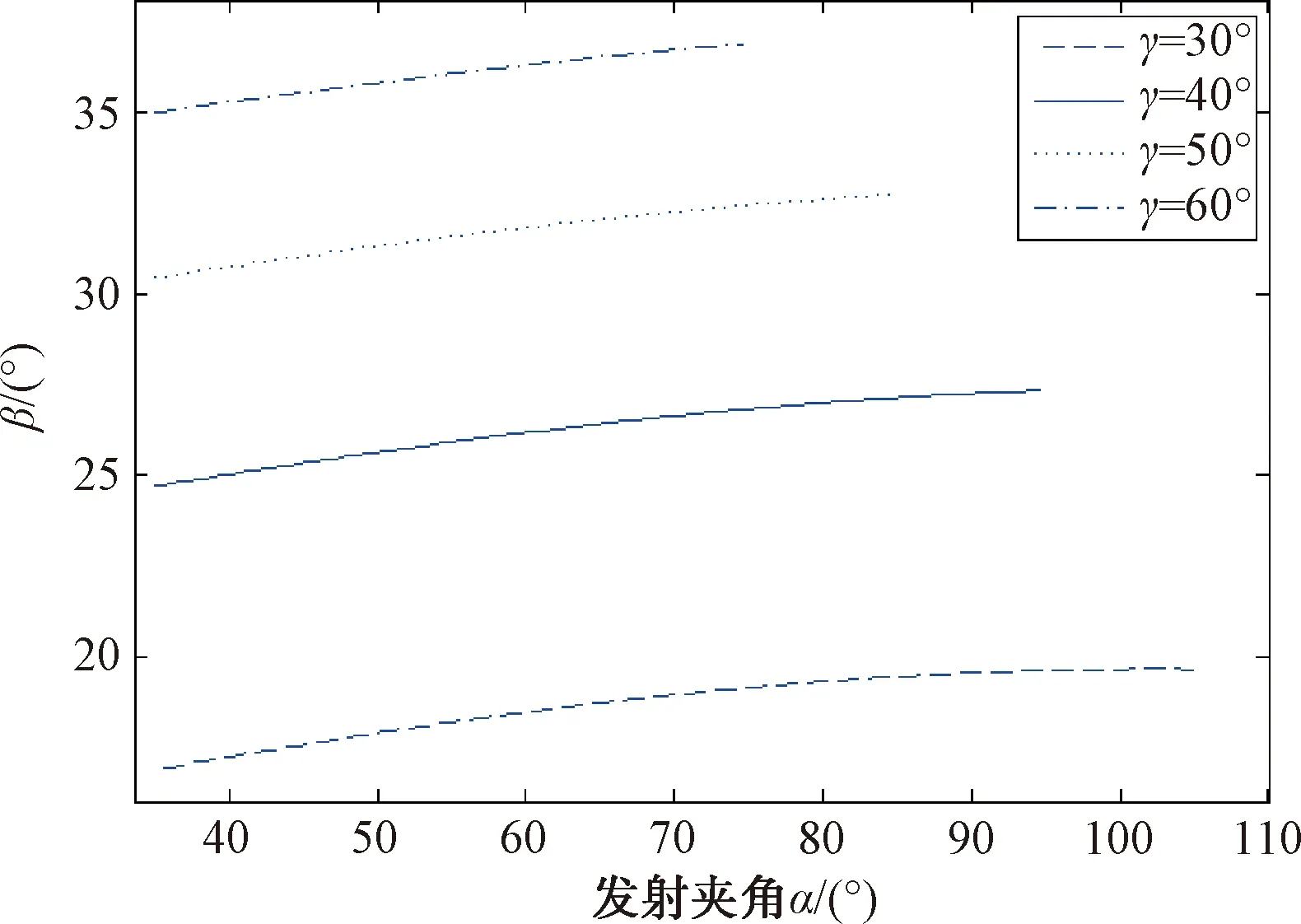
图12 队列角不同时导弹对邻舰的威胁随发射夹角变化图
(3) 舰艇间距越大,E舰越容易进入被引偏的导弹的末制导雷达波束内,越容易受到威胁,如图13所示。
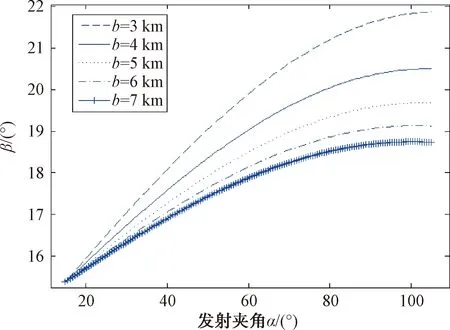
图13 舰艇间距不同时导弹对邻舰的威胁随发射夹角变化图
(4) 箔条云的雷达反射面积越大,即质心越接近云团,质心距离d越大,这种情况下对E舰威胁也越小,如图14所示。
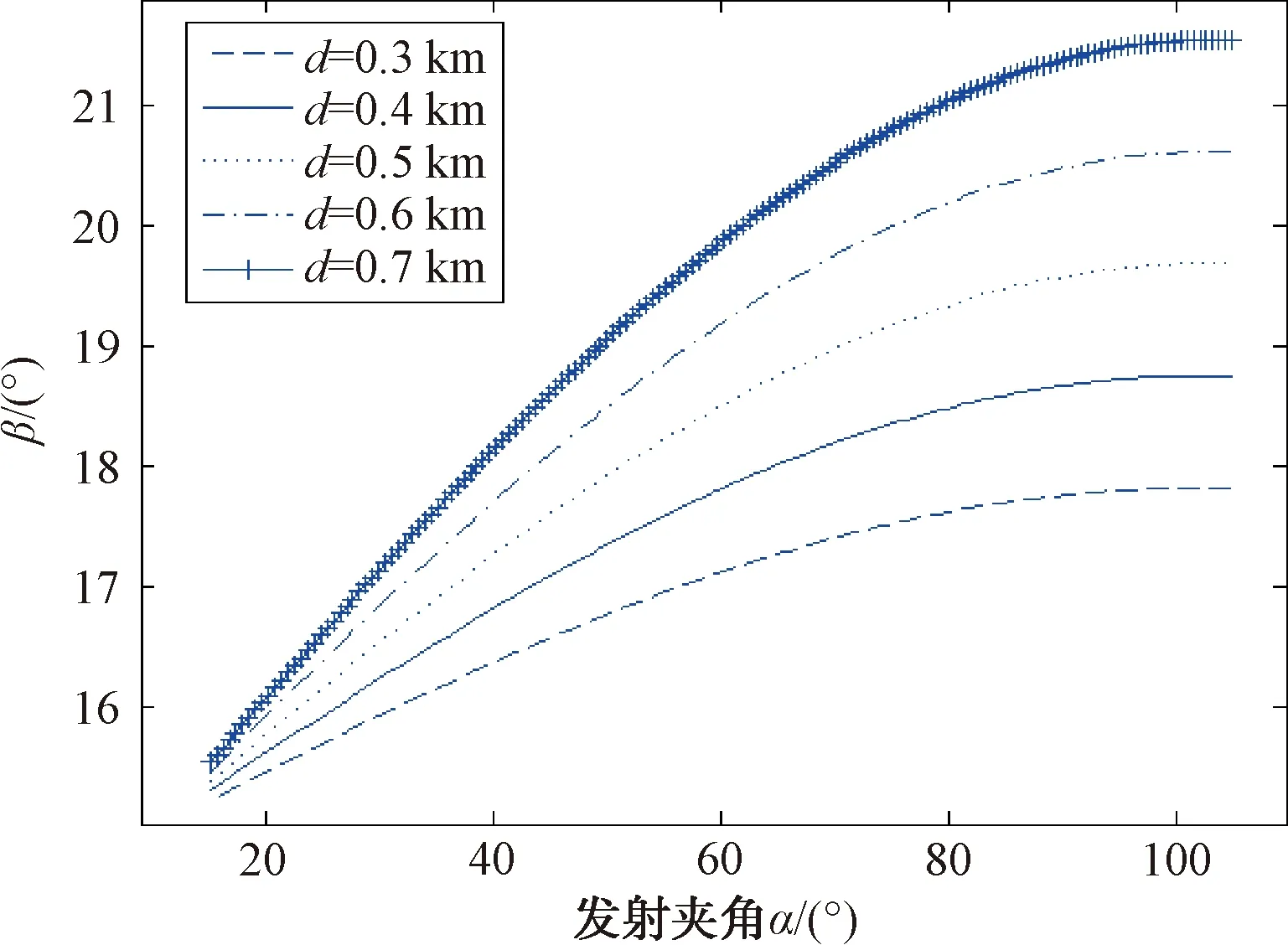
图14 不同质心距离时导弹对邻舰的威胁随发射夹角变化图
3.3 二次质心干扰策略
导弹被目标舰艇的质心干扰引偏后,可能对邻舰造成威胁。这种情况下,邻舰也可使用质心干扰(称为二次质心干扰),协同将导弹引偏至脱离编队,保证编队安全[2]。
根据3.1节的计算,方位队列时,舰艏或舰艉方向45°范围内入射的导弹在引偏后容易对邻舰造成威胁。图15所示为方位队列舰艇编队二次质心干扰图。
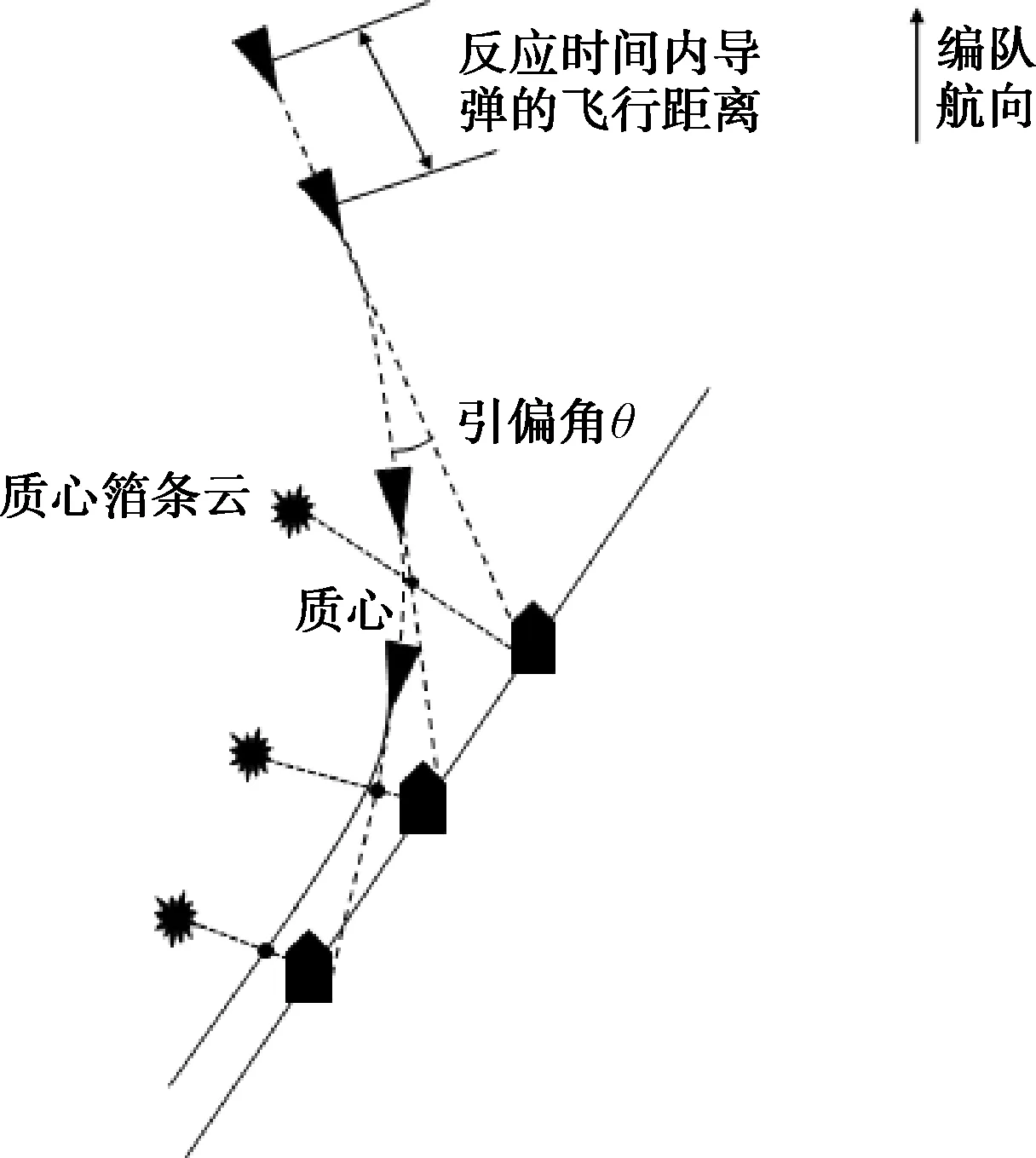
图15 方位队列舰艇编队二次质心干扰图
对于像人字队列这样的复式队列,导弹被引偏后的情况有多种,因此考虑条件较为复杂。目标舰艇同侧邻舰实施质心干扰的情形与方位队列类似,如图16所示。当导弹穿过编队某一侧的队列线后,另一侧的舰艇就需要视导弹来袭方向实施二次质心干扰,如图17所示。
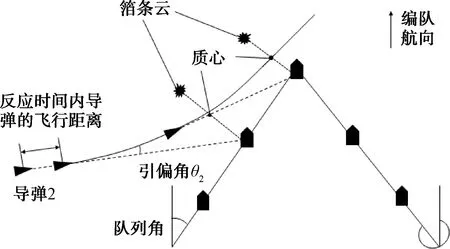
图16 人字队列舰艇编队二次质心干扰图1
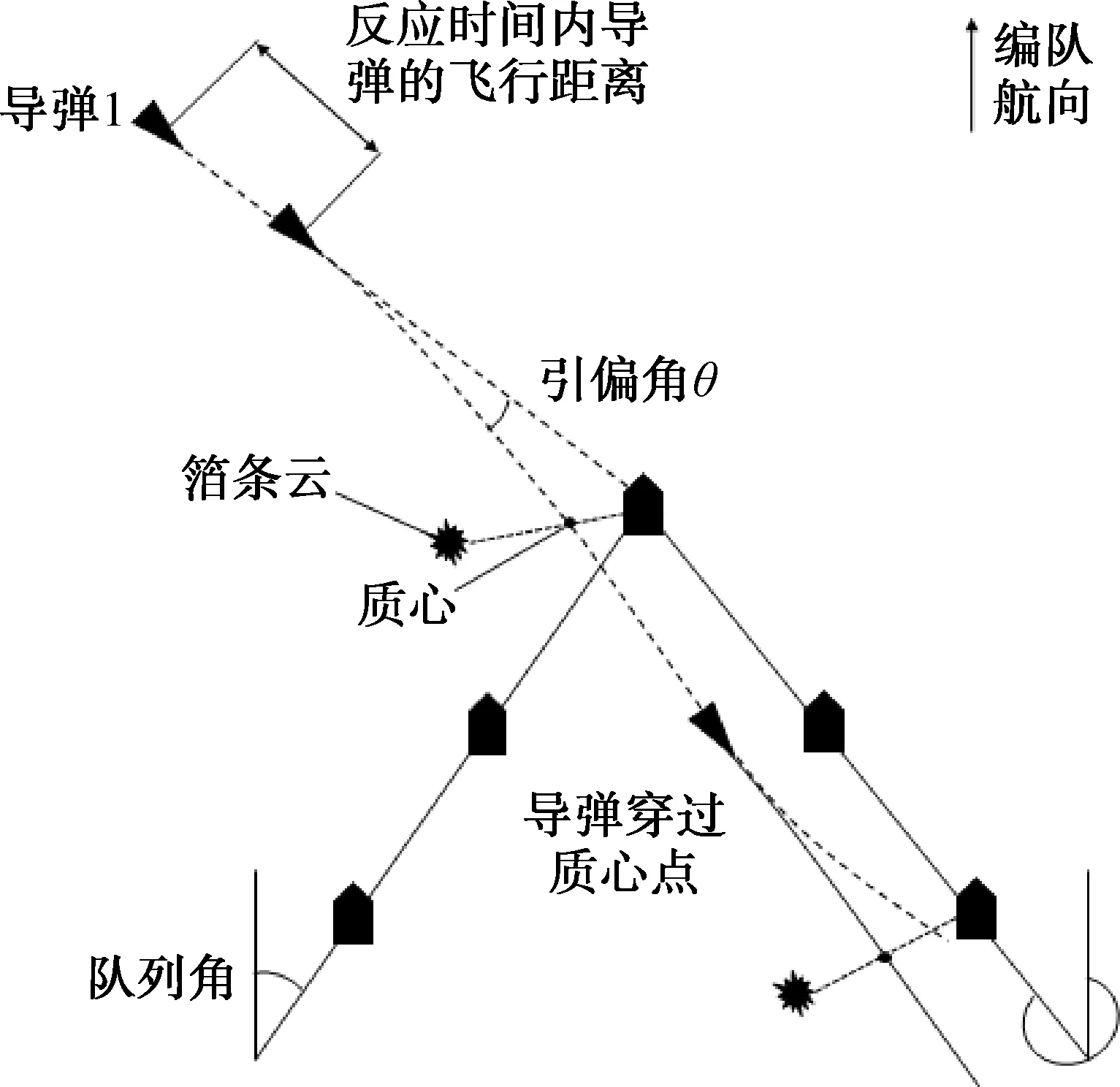
图17 人字队列舰艇编队二次质心干扰图2
4 结束语
文章旨在通过一种较为简单的计算方法,分析导弹引偏效果,建立目标舰艇实施质心干扰与编队受导弹二次威胁之间的关联关系,以计算仿真的方法,通过定性和定量给出编队质心干扰策略。计算方法较为便捷,对于舰艇编队快速判断威胁并拟定质心干扰策略有一定帮助。
